ESERCITAZIONE

1_TRAVATURA RETICOLARE SIMMETRICA

 

 

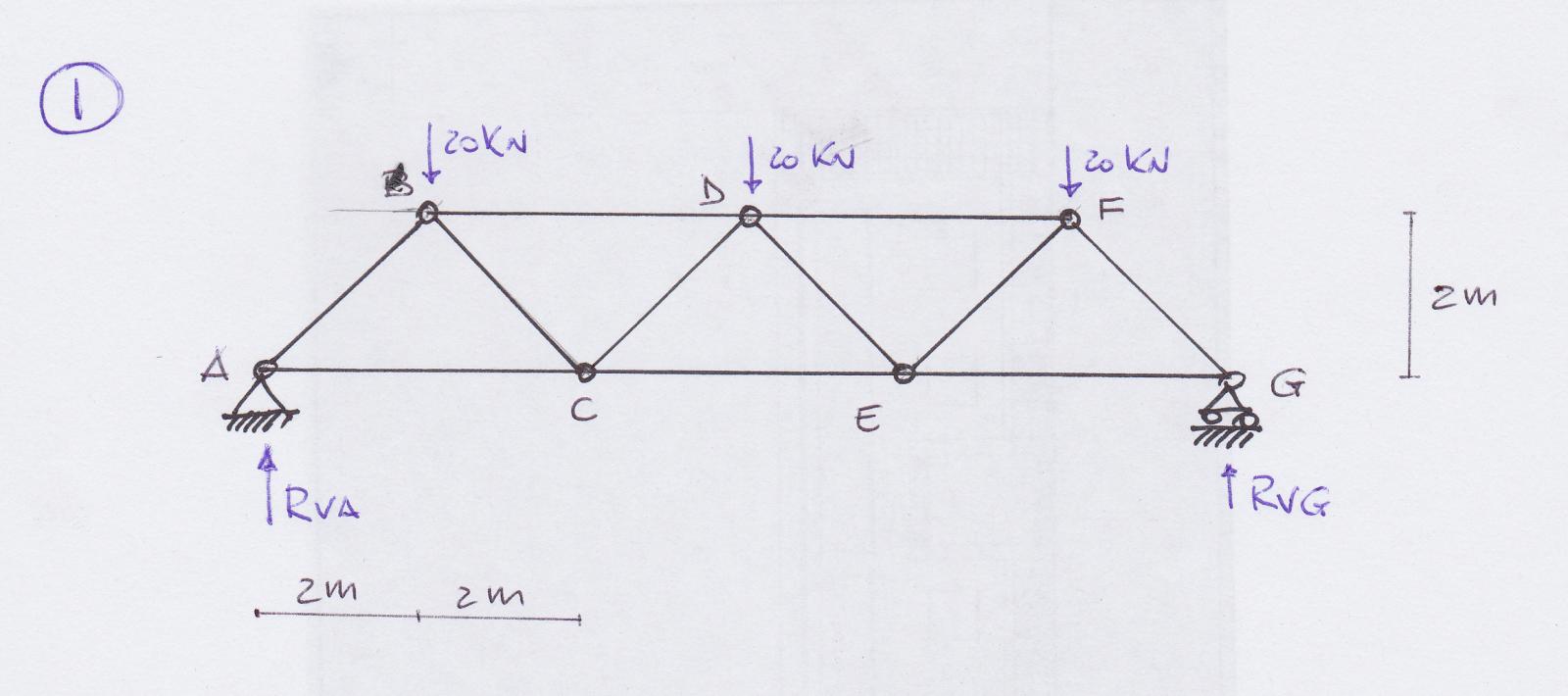
In questa prima esercitazione andremo ad analizzare una travatura reticolare isostatica simmetrica, tipologia strutturale formata da puntoni e tiranti collegati tra loro da due cerniere. La configurazione analizzata è simmetrica sia per struttura che nella ripartizione delle forze sui nodi, quindi basterà risolvere metà della struttura per  avere il risultato completo.

 

Per prima cosa bisognerà verificare l’isostaticità della struttura, confermando che il numero di gradi di libertà della struttura sia pari al numero dei vincoli che agiscono su di essa. Possiamo avvalerci di due metodi:

1)  L=V (il numero gradi di libertà è uguale al numero gradi di vincolo)

V = V_e + V_i   nel nostro caso V=33

L= 3 x numero corpi  nel nostro caso 3x11= 33

2)  V_e + a = 2 nodi (vincoli esterni+ numero aste = numero nodi x 2)

3 + 11 = 2 x 7      = 33

 

Andiamo dunque a calcolare le reazioni vincolari. Ciascun nodo superiore è sottoposto ad una forza verticale di 20 KN , ed essendo la nostra una struttura simmetrica, le reazioni verticali avranno stessa intensità nei nodi A e G. Bisognerà dunque ripartire equamente le forze esterne applicate alla struttura.

Rva=Rvg = 60/2 = 30 KN

 

Risolviamo la struttura attraverso il metodo delle sezioni di Ritter, andando a sezionare virtualmente la trave in due parti, tagliando tre aste non convergenti nello stesso punto.

Isolando una delle due porzioni, calcoleremo gli sforzi assiali attraverso l’equazione di equilibrio dei momenti nel nodo scelto.

 

PRIMA SEZIONE

 

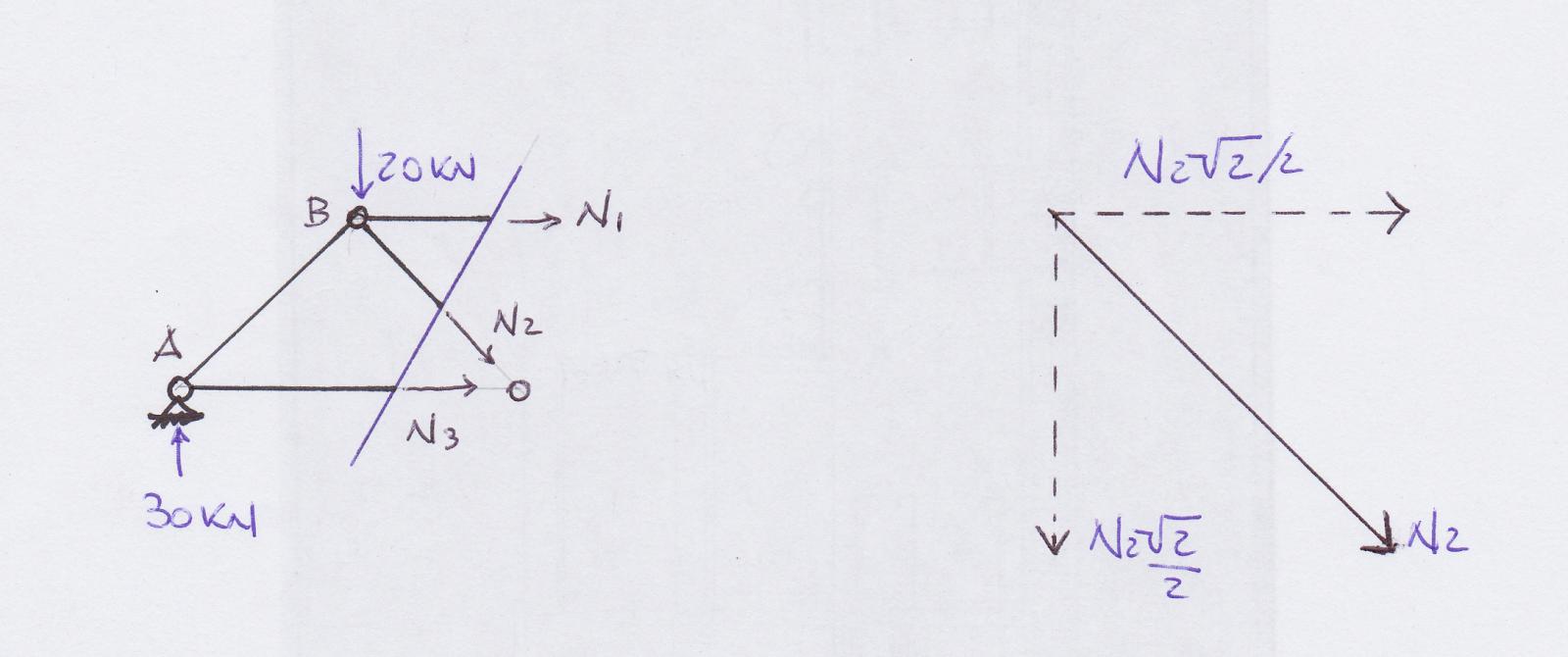
Evidenziamo gli sforzi normali delle singole aste sezionate, ipotizzando che il verso è uscente, ovvero che le aste sono sottoposte a trazione.

Attraverso l’equilibrio dei momenti intorno al nodo C ricaviamo il valore di N₁.

∑Mc=0  == (30x4)-(20x2)+(N₁x2)=0  ==  2N₁= -80/2  

N₁= -40 KN    quindi l’asta è COMPRESSA. Il verso ipotizzato era sbagliato.

 

Equilibrio dei momenti intorno al nodo B per ricavare lo sforzo normale N₃.                              

∑Mb=0  ==  (N₃x2)-(30x2)=0  ==  2N₃=60/2 KN  

N₃=  30 KN    quindi l’asta è TESA. Il verso ipotizzato è giusto.

 

L’asta BC è inclinata di 45°, dobbiamo dunque scomporre la forza in una componente verticale ed una orizzontale per calcolare il valore dello sforzo normale N₂.  Tramite l’equilibrio delle forze verticali calcolo l’incognita N₂.

∑Fy=0  == 30-20-N₂√2/2=0  

N₂= 10√2 KN   quindi l’asta è TESA. Il verso ipotizzato è giusto.

 

SECONDA SEZIONE

 

∑Fx=0  ==  30+N₄√2/2=0  ==  N₄√2/2=-30  

N₄=-30√2 KN   quindi l’asta è COMPRESSA.

 

TERZA SEZIONE

 

Attraverso l’equilibrio dei momenti intorno al nodo D ricaviamo lo sforzo normale N₅

∑Md=0  == (N₅x2)+(20x4)-(30x6)=0  ==  2N₅+80-180/2=0  

N₅= 50 KN  quindi l’asta è TESA. 

Tramite l’equilibrio delle forze verticali calcolo N₆.

∑Fy=0  ==  N₆√2/2+30-20=0  

N₆= -10√2 KN  quindi l’asta è COMPRESSA.

Poiché la struttura è simmetrica, i risultati ottenuti nella prima metà della trave possono essere applicati alla seconda metà.

 

 

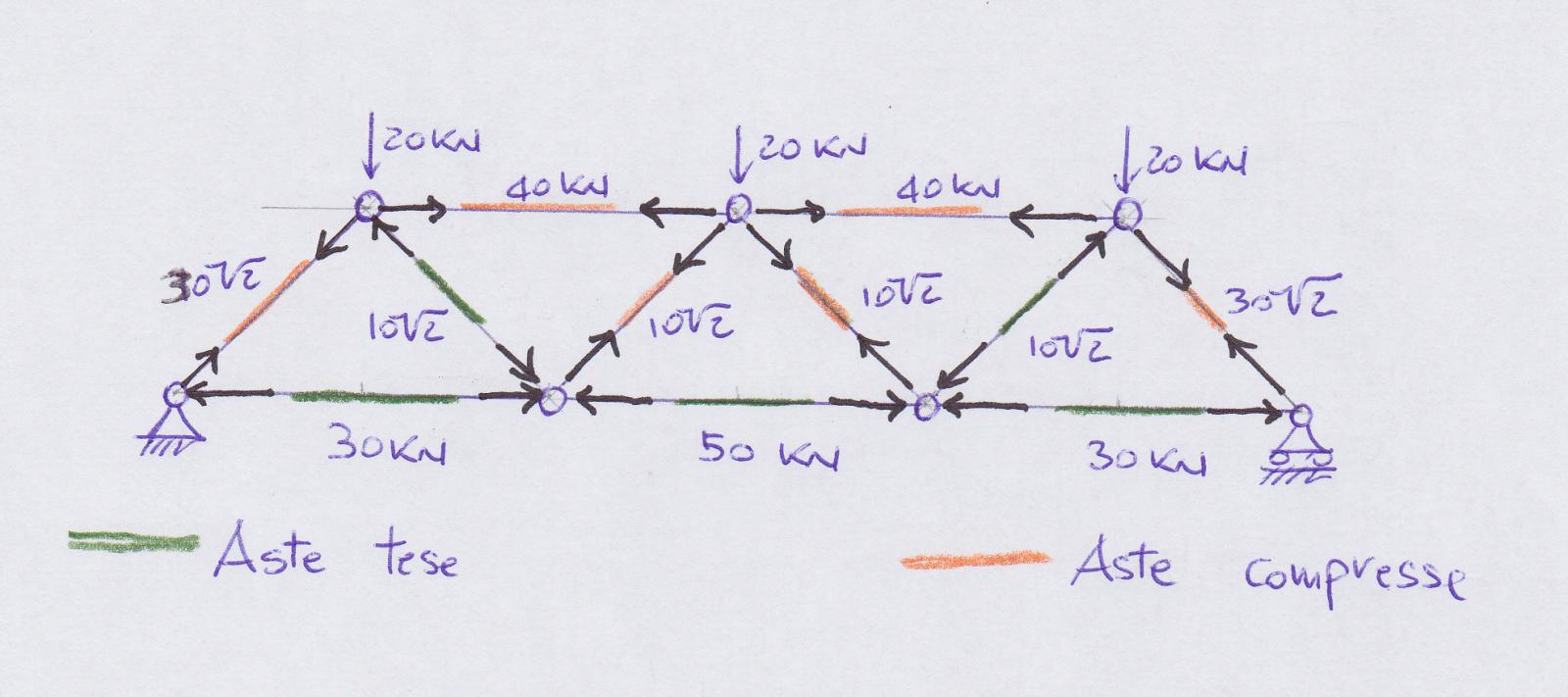
Infine utilizzeremo il programma SAP 2000  per avere conferma dei risultati e dei grafici ottenuti, ridisegnando la struttura e applicando le forze esterne sui nodi.

 

 

GRAFICO DELLA DEFORMATA

 

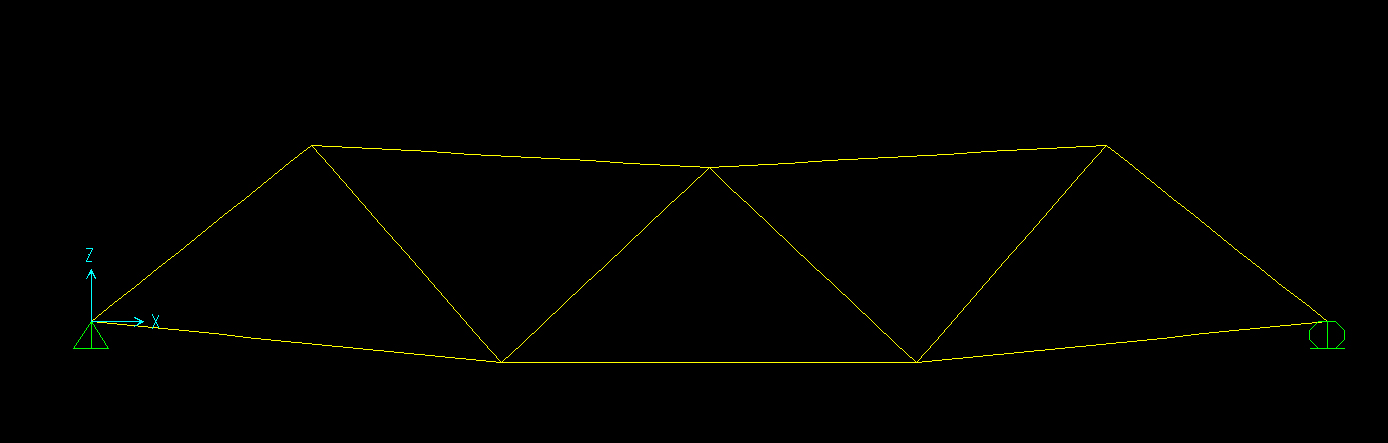
GRAFICO DELLO SFORZO NORMALE

 

 

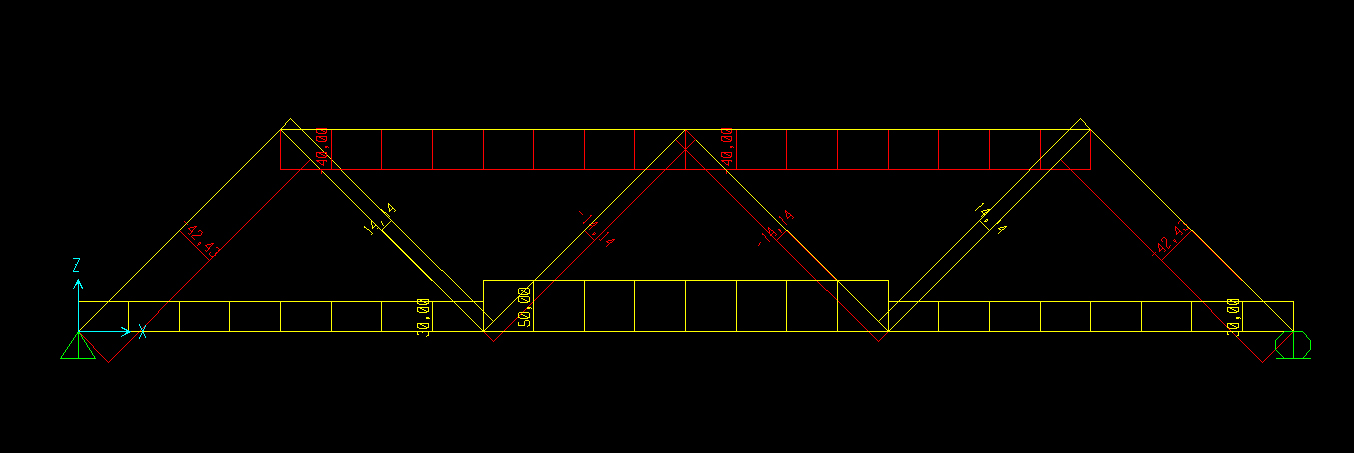
2_TRAVATURA RETICOLARE ASIMMETRICA

 

Questa seconda esercitazione verte su una travatura reticolare asimmetrica, non potendo risolvere solo metà struttura, dovremo dunque risolverla tutta.

 

Il primo passo è la verifica dell'isostaticità:

1) V_e + a = 2 x 7

3 + 11 = 2 x 7

14=14       ISOSTATICA

Calcoliamo ora le reazioni vincolari.

 

∑Fy=0  ==   RvA-10-10=0  ==  RvA= 20 KN

∑Mb=0  ==  -(10x1)-(10x2)+(RuHx1)=0  ==  RuH= 30 KN       RuA= 30 KN

 

Andremo a risolvere la struttura attraverso il metodo dei nodi. Isoliamo un nodo della struttura reticolare andando a tagliare le aste che vi convergono, calcolando il valore dello sforzo assiale trasmesso dalle aste al nodo attraverso il l’equilibrio delle forze.

 

NODO A - NODO B

Nodo B

Le aste che convergono nel Nodo B sono scariche.

N₁=0      N₂=0

Nodo A

∑Fy=0  == 20+N₃√2/2=0  

N₃= -20√2 KN  l’asta è COMPRESSA.

∑Fx=0  ==  N₃√2/2+N₄+30=0  

N₄= -10 KN   l’asta è COMPRESSA.

 

NODO C - NODO D

Nodo C

N₅=0  l’asta è SCARICA.

∑Fx=0  ==  N₈+10=0  

N₈= -10 KN   l’asta è COMPRESSA.

 

Nodo D

∑Fx=0  ==  10+N₆√2/2-(20√2x√2/2)=0  ==  10+N₆√2/2-20=0

N₆=10√2 KN  l’asta è TESA.

∑Fx=0  == N₇+N₆√2/2-(20√2x√2/2)=0  ==  N₇+(10√2x√2/2)+20=0

N₇=-30 KN   l’asta è COMPRESSA.

 

NODO E - NODO G - NODO H

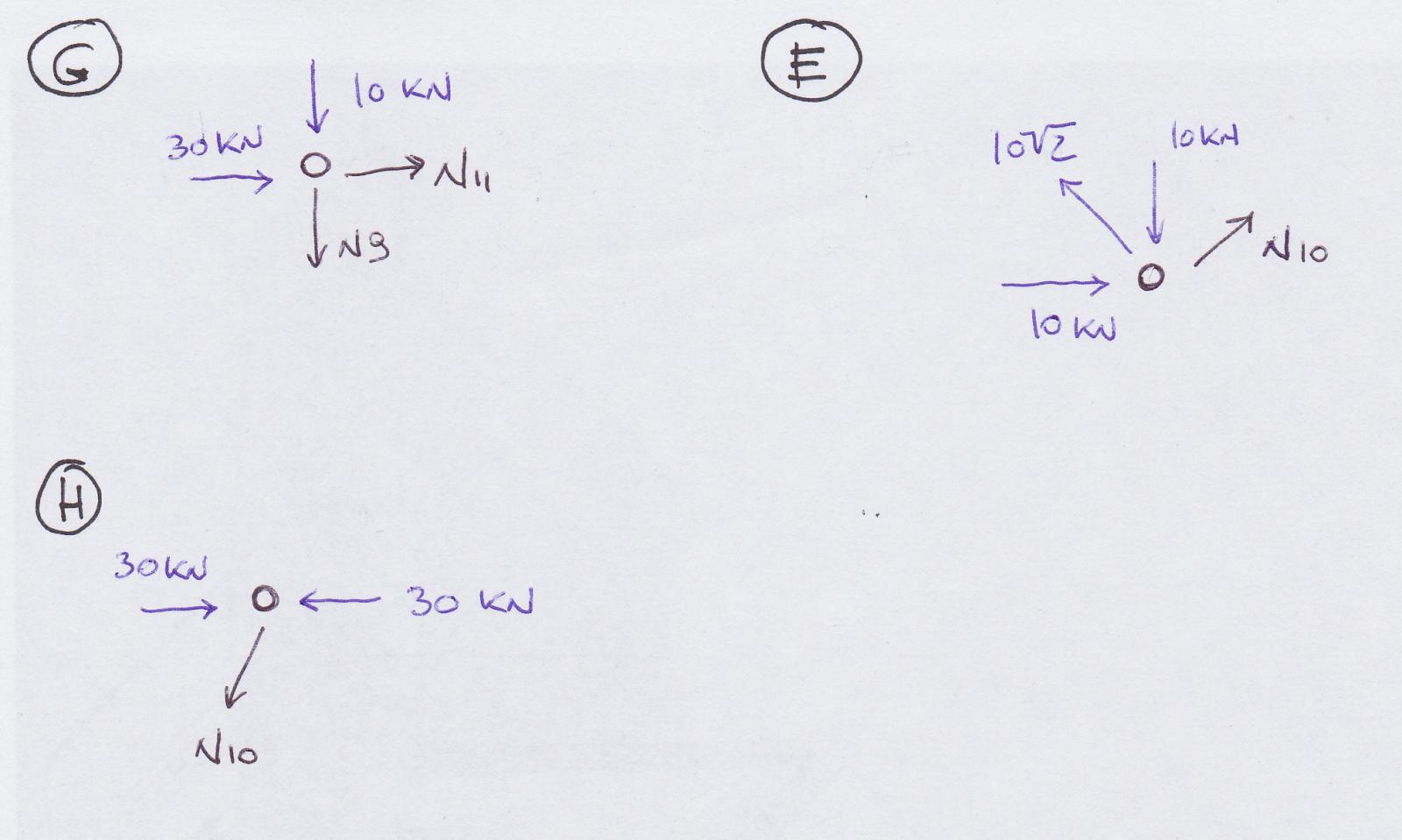
Nodo G

∑Fx=0  ==  N₉+10=0  

N₉= -10 KN   l’asta è COMPRESSA.

∑Fx=0  ==  N₁₁+30=0  

N₁₁= -30 KN   l’asta è COMPRESSA.

Nodo E

∑Fx=0  ==  N₁₀√2/2+10-(10√2x√2/2)=0  ==  N₁₀√2/2=10-10

N₁₀=0  l’asta è SCARICA.

Nodo H

N₁₀=0  l’asta è SCARICA.

 

 

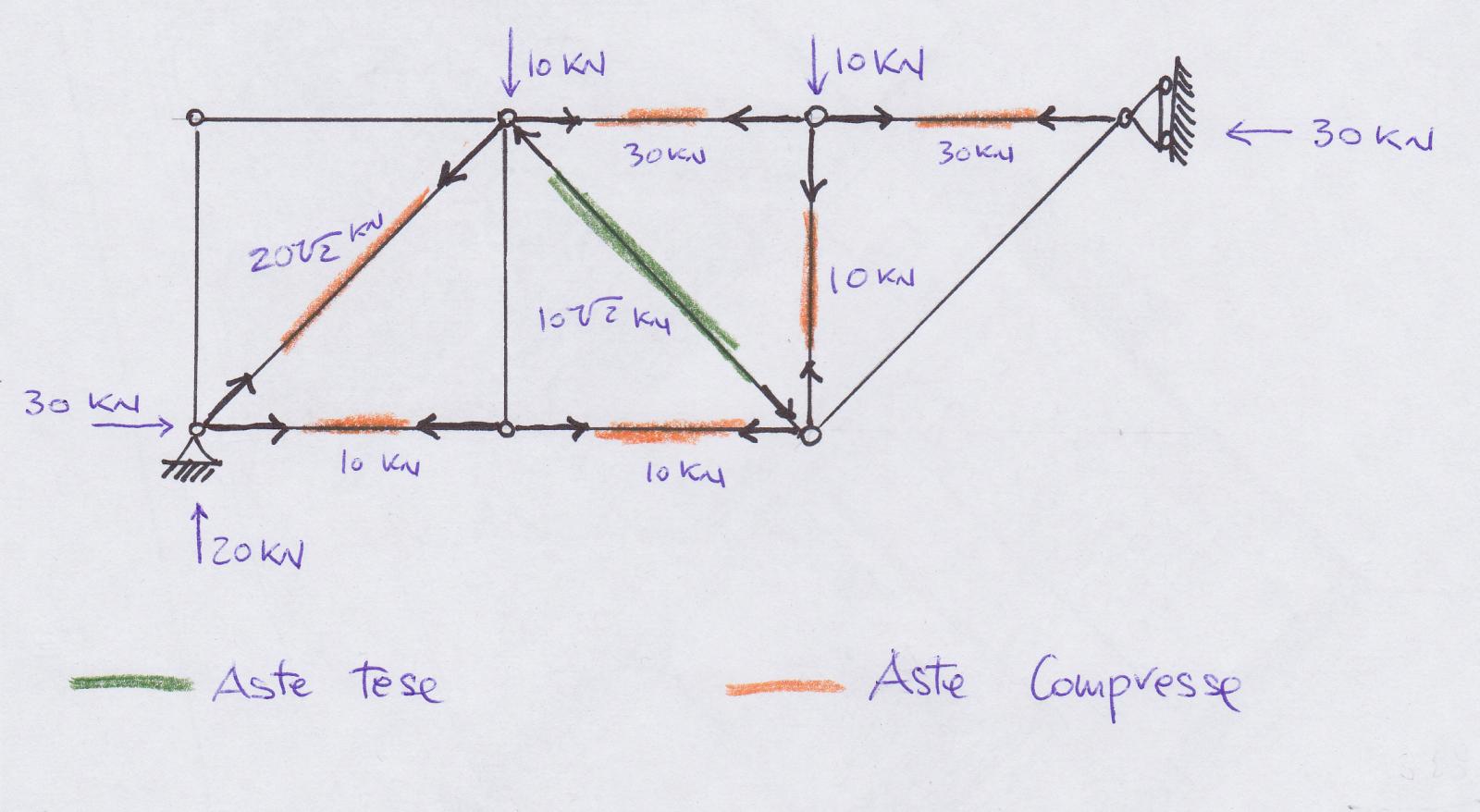
Come ultimo passaggio, per avere conferma dei calcoli appena svolti, disegniamo la struttura su SAP 2000. Ottengo cosi il diagramma degli sforzi assiali e la simulazione della deformata della trave.

 

GRAFICO DELLA DEFORMATA

 

GRAFICO DELLO SFORZO NORMALE

 

 

3_ARCO A TRE CERNIERE CON CARICO DISTRIBUITO LATERALMENTE

 

Questa terza esercitazione verte su una struttura avente due corpi collegati da una cerniera interna e due cerniere alla base. Il carico q distribuito sul primo corpo rende la struttura non simmetrica.

Il primo passo per risolvere questa struttura è il calcolo delle reazioni vincolari. Dividiamo quindi l’arco in due corpi.

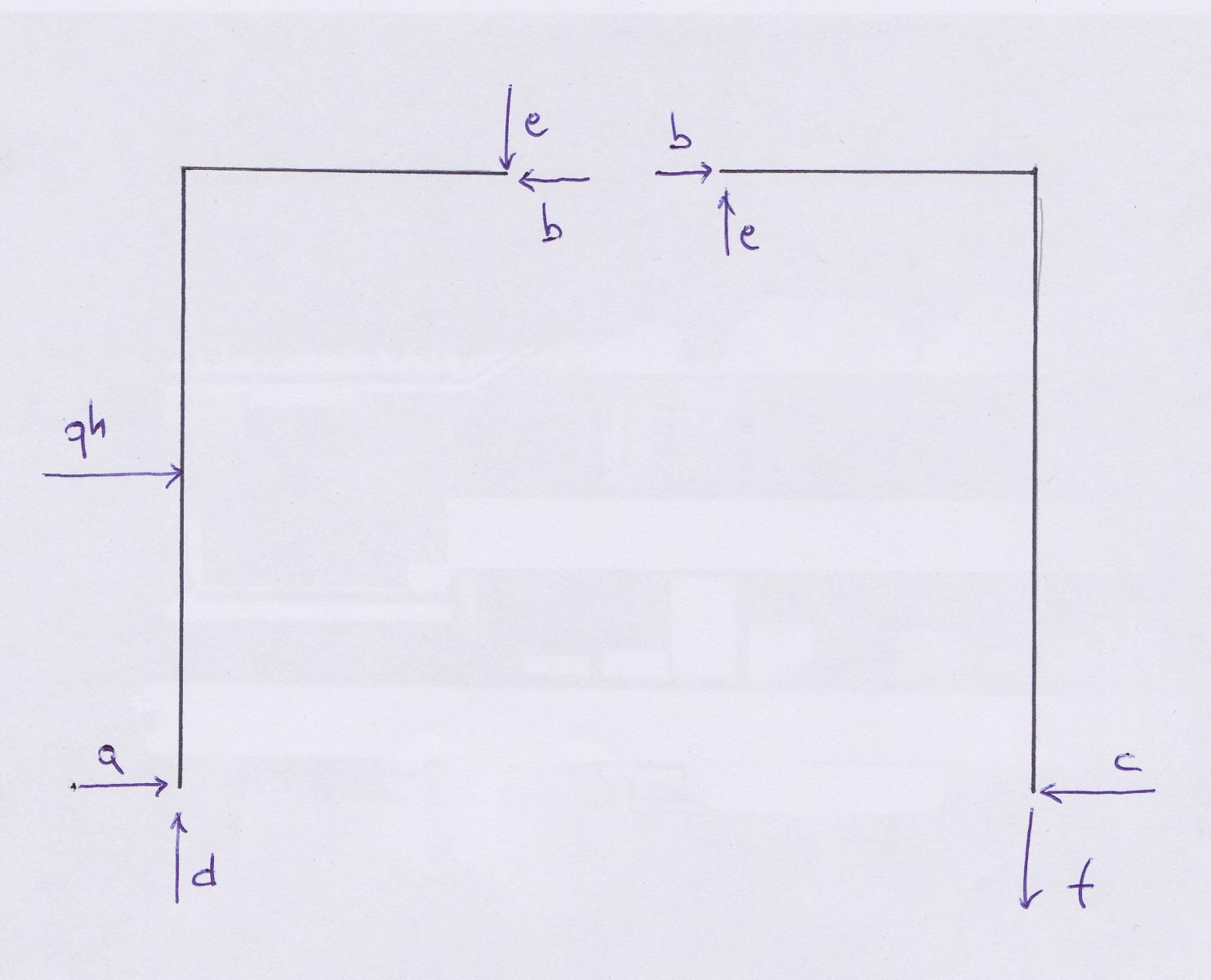
Ottengo il valore della singole forze agenti sulla struttura attraverso  l’equilibrio dei momenti sulle cerniere.

Le forze orizzontali bloccate dalle cerniere esterne, di valore di 3qh/4 e qh/4,hanno stesso verso, andando a contrastare il carico distribuito esterno del valore di qh.

DIAGRAMMI N,T,M

Sforzo Normale

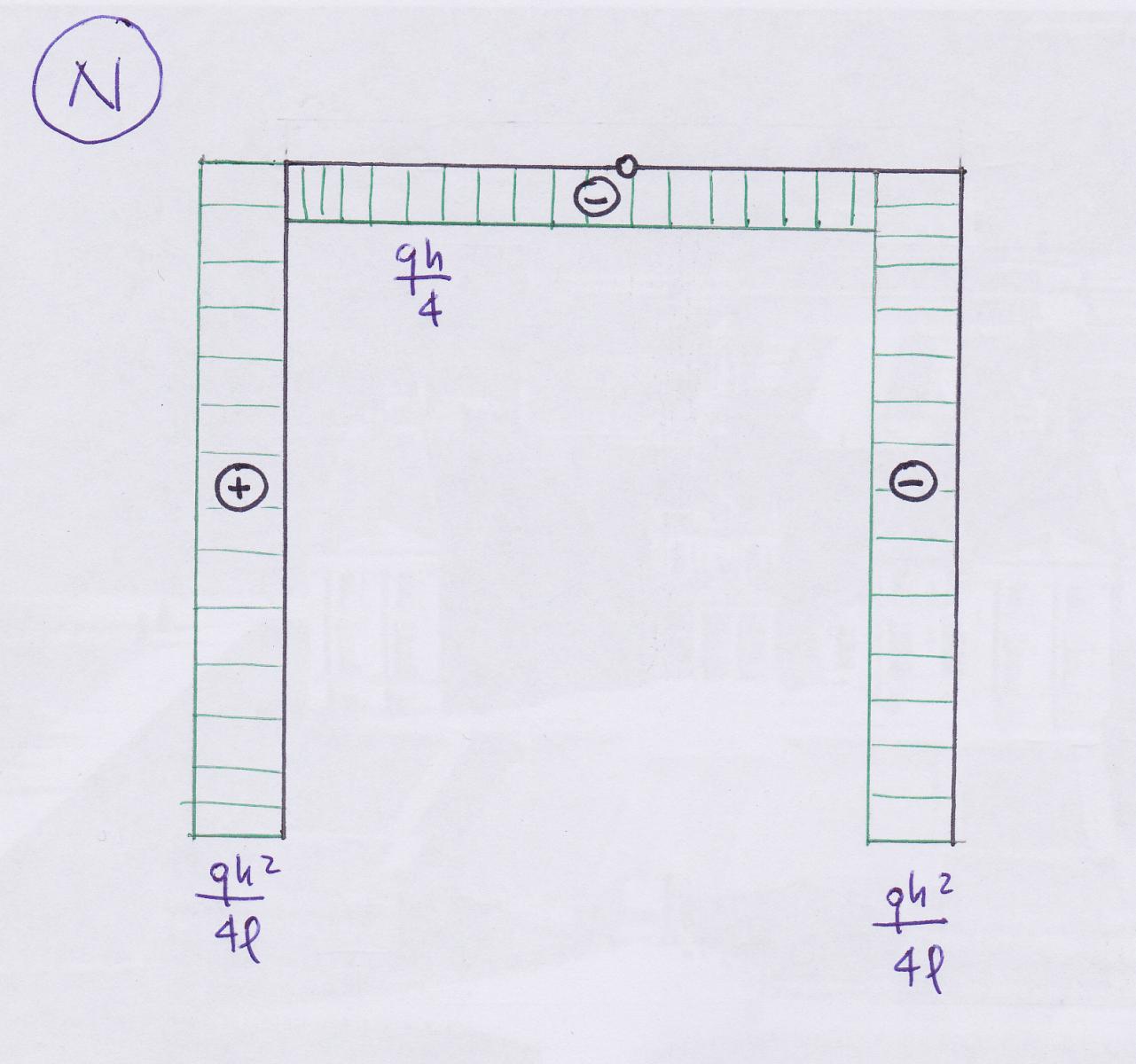
Nel diagramma possiamo notare che l’andamento è costante in tutta la struttura, non essendo presenti carichi concentrati. I valori sono positivi se agli estremi delle aste sono presenti sforzi di trazione, viceversa, saranno negativi se sono presenti sforzi di compressione.

Sforzo di Taglio

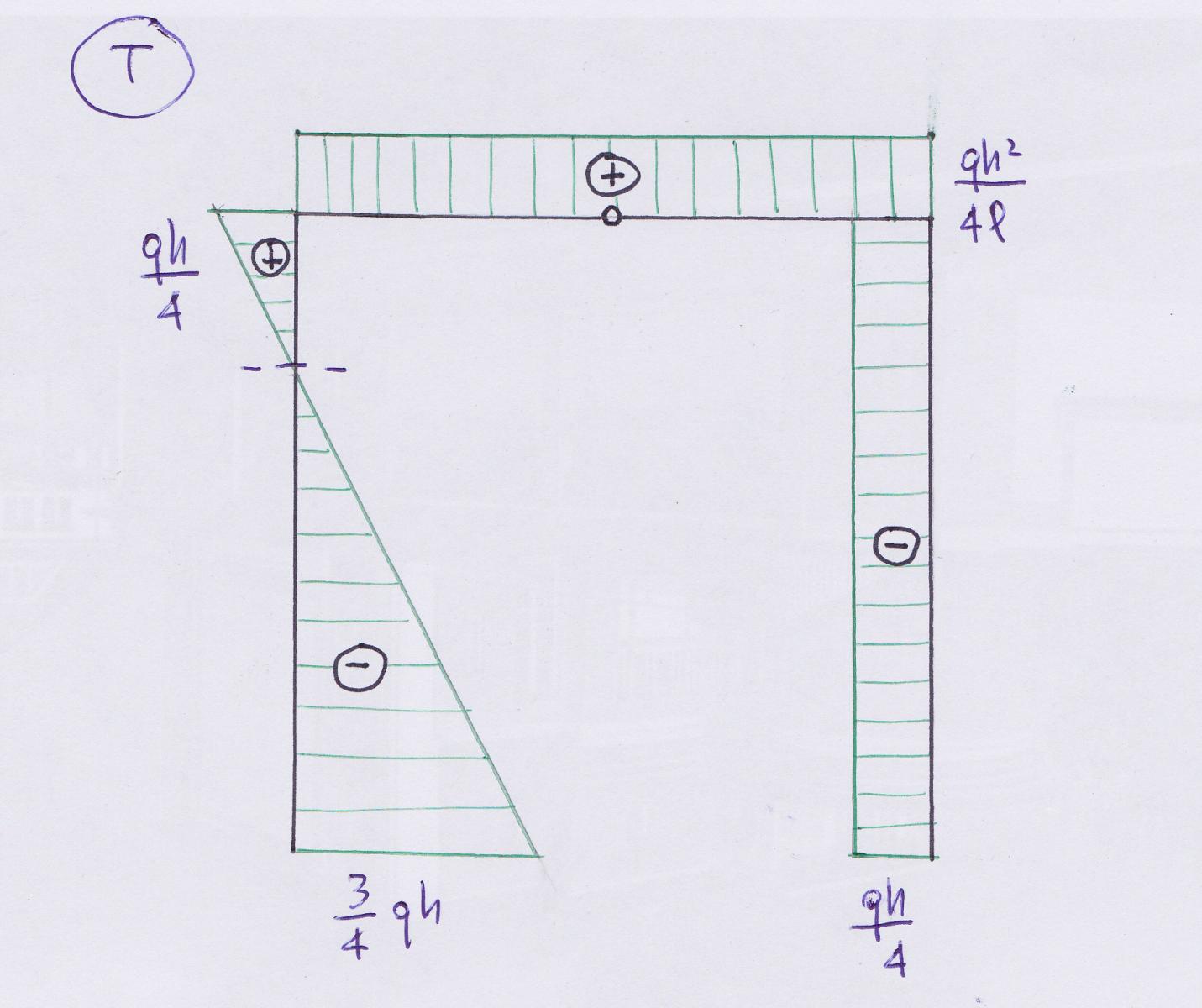
Sulla prima asta lo sforzo di taglio assume un andamento lineare, in quanto è presente un carico distribuito perpendicolare  che agisce su di essa. Nella aste restanti i diagrammi sono costanti, assumendo valori negativi o positivi a seconda delle forze orizzontali all’estremità del tratto di asta preso in considerazione.

Momento

Il diagramma del momento sulla prima asta è parabolico, ed avrà un massimo nel punto in cui il diagramma del taglio si annulla. Nel resto della struttura i diagrammi restano lienari.

Verifica con SAP 2000

Q = 10 KN      H = 2m      L = 1m

GRAFICO DELLA DEFORMATA

DIAGRAMMA DELLO SFORZO NORMALE

DIAGRAMMA DELLO SFORZO DI TAGLIO

DIAGRAMMA MOMENTO

 

 

4_DIMENSIONAMENTO TRAVI

L’edificio scelto per questa esercitazione è la mensa universitaria all’interno dell’ex mattatoio di Roma . Il solaio che ho analizzato è quello del primo livello, dove è ubicata la sala mensa con circa 180 posti a sedere, al di sopra delle cucine, dei magazzini e degli spogliatoi. La struttura è simmetrica. Le travi hanno una luce di 9,80 metri ed una campata di 5,50 metri,  eccetto quella centrale che misura 7,50 metri. La trave selezionata per l’esercizio è una delle due centrali, con campata irregolare di 6,50 m. Avendo un’area d’influenza maggiore delle altre, sarà quella subirà maggiormente il peso del solaio.

 

Carichi da prendere in considerazione per il dimensionamento della trave:

- Carichi strutturali = comprendono il peso proprio degli elementi strutturali.

- Carichi permanenti = sono i carichi legati agli elementi non strutturali che compongono gli strati del solaio come pavimenti, massetti, impianti, controsoffitti, tramezzature ed intonaci.

- Carichi accidentali = carichi legati alla funzione dell'edificio, con valori tabellati che variano a seconda della categoria.

TRAVE IN ACCIAIO

Trave secondaria

Luce: 6,50m (campata maggiore)

Interasse:  1m

Qa (carichi accidentali): 3,00 KN/mq

- Edificio in categoria C, Ambienti suscettibili ad affollamento, Cat. C1

Qs (carico strutturale): 2,50 KN/mq

- Lamiera grecata HI-BOND A55/P600  spessore lamiera 8mm H 8cm

- Getto in calcestruzzo con rete elettrosaldata H 15 cm

Qp (carichi permanenti): 1,9 KN/mq

- Pavimento in lastre di Gres Porcellanato, H 12 mm = 0,2 KN/mq

- Massetto con serpentina riscaldamento, H 6 cm = 1,1 KN/mq

- Ipotesi d'incidenza impianti = 0,50 KN/mq

- Controsoffitto in pannelli di gesso H 12mm = 0,1 KN/mq

Q= Qa + Qs + Qp x interasse (carico totale al metro lineare) =  7,4 KN/m

 

Dimensionamento trave secondaria

Inserisco i dati nelle caselle corrispondenti del foglio Excel e determino il modulo di resistenza a flessione Wx .

Scelgo dunque la IPE adeguata ai miei valori: IPE 200 H 20 cm B 10 cm

In tabella la trave ha un peso di 0,22 KN/m, che al mq si trasformano in 0,22 KN/interasse = 0,22/1 = Qtr = 0,22 KN/mq.

Q's= (Qs+Qtr) = 2,50 + 0,22 = 2,72 KN/mq

Ricalcolato il peso con il foglio Excel ho la conferma che la IPE da me scelta riesce a supportare il suo peso.

 

Trave principale

Luce: 9,80 m

Interasse:  6,50 m (campata maggiore)

Qa (carichi accidentali): 3,00 KN/mq

Qs (carico strutturale): 2,72 KN/mq

Qp (carichi permanenti): 1,9 KN/mq

Q= Qa + Qs + Qp x interasse (carico totale al metro lineare) =  49,53 KN/m

 

Dimensionamento trave

Inserisco i dati nelle caselle corrispondenti del foglio Excel e determino il modulo di resistenza a flessione Wx .

 

Scelgo dunque la IPE adeguata ai miei valori: IPE 550 H 55 cm B 21 cm

 

In tabella la trave ha un peso di 1,06 KN/m, che al mq si trasforma in 1,06 KN/interasse = 1,06/6,5 = Qtr = 0,163 KN/mq. 

Q’s= (Qs+Qtr) = 2,72 + 0,163 = 2,883 KN/mq

Ricalcolato il peso con il foglio Excel ho la conferma che la IPE da me scelta riesce a supportare il suo peso.

 

TRAVE IN LEGNO

 

Travetto

Luce: 6,50m (campata maggiore)

Interasse:  1m

Qa (carichi accidentali): 3,00 KN/mq

- Edificio in categoria C, Ambienti suscettibili ad affollamento, Cat. C1

Qs (carico strutturale): 0,18 KN/mq

- Tavolato, H 3cm = 0,18 KN/mq

Qp (carichi permanenti): 1,9 KN/mq

- Pavimento in lastre di Gres Porcellanato, H 12 mm = 0,2 KN/mq

- Massetto con serpentina riscaldamento, H 6 cm = 1,1 KN/mq

- Ipotesi d'incidenza impianti = 0,50 KN/mq

- Controsoffitto in pannelli di gesso H 12mm = 0,1 KN/mq

Q= Qa + Qs + Qp x interasse (carico totale al metro lineare) =  5,08 KN/m

 

Dimensionamento travetto

Legno utilizzato = Abete Rosso

Struttura = Struttura in legno lamellare standard

Classe resistenza= GL 32

Inserisco i dati nel foglio Excel ed ottengo il carico a metro lineare.  Ipotizzando una base di 20 cm per il travetto, ottengo un’altezza di 27,01 cm che arrotonderò a 30 cm .

 

Peso specifico legno lamellare = 410 Kg/mc (UNI EN 1194)

Peso Travetto per metro lineare = (0,20 m x0,40 m x 4,1 KN/mc) = 0,328 KN/m

Peso distribuito travetto  = 0,328 KN/m / 1 m interasse = 0,328 KN/mq

Modifico quindi il foglio Excel con il nuovo carico.   Q = (5,08+0,328) = 5,408 KN/m

Ricalcolato il peso con il foglio Excel ho la conferma che il travetto da me scelto è corretto.

Travetto = b 20 cm H 30 cm

 

Trave principale

Luce: 9,80 m

Interasse:  6,50 m (campata maggiore)

Qa (carichi accidentali): 3,00 KN/mq

Qs (carico strutturale): 0,508 KN/mq

(0,18+0,328 peso travetto)

Qp (carichi permanenti): 1,9 KN/mq

Q= Qa + Qs + Qp x interasse (carico totale al metro lineare) =  35,152 KN/m

 

Dimensionamento trave

Legno utilizzato = Abete Rosso

Struttura = Struttura in legno lamellare standard

Classe resistenza= GL 32

Inserisco i dati nel foglio Excel ed ottengo il carico a metro lineare.  Ipotizzando una base di 40 cm per la trave, ottengo un’altezza di 75,78 cm che arrotonderò ad 80 cm .

 

Peso specifico legno lamellare = 410 Kg/mc (UNI EN 1194)

Peso Trave per metro lineare = (0,40 m x0,80 m x 4,1 KN/mc) = 1,312 KN/m

Peso distribuito trave  = 1,312 KN/m / 6,5 m interasse = 0,201 KN/mq

Modifico quindi il foglio Excel con il nuovo carico.   Q = (35,152+0,201) = 36,458 KN/m

Ricalcolato il peso con il foglio Excel ho la conferma che il travetto da me scelto è corretto.

Trave = b 40 cm H 80 cm

TRAVE IN CLS

 

Trave

Luce: 9,80 m

Interasse:  6,50 m (campata maggiore)

Qa (carichi accidentali): 3,00 KN/mq

- Edificio in categoria C, Ambienti suscettibili ad affollamento, Cat. C1

Qs (carico strutturale): 3,17 KN/mq

- Solaio Tralicciato SIAI H 20 cm + 5 cm soletta

(Valore Tabellare)

- Soletta, H 15 cm = 1,25 KN/mq

- Pignatta, H 20cm, Base 35cm, peso specifico 66 Kg/mc, N° pignatte m=2 = 0,92 KN/mq

- Travetti, H 17cm , Base 12cm, peso specifico: 25 Kc, N° tarvetti m=2 = 1 KN/mq

Qp (carichi permanenti): 1,9 KN/mq

- Pavimento in lastre di Gres Porcellanato, H 12 mm = 0,2 KN/mq

- Massetto con serpentina riscaldamento, H 5 cm = 1,1 KN/mq

- Ipotesi d'incidenza impianti = 0,50 KN/mq

- Controsoffitto in pannelli di gesso H 12mm = 0,1 KN/mq

Q= Qa + Qs + Qp x interasse (carico totale al metro lineare) =  52,55 KN/m

 

Acciaio impiegato per l’armatura = B450C
(zona sismica)

Momento Massimo Tensione = 450 Mpa

Valore di Rottura = 540 Mpa

Allungamento a Rottura  ε =7 %

fy/ y_m= (450 N/mm²) / 1,15 = 391,30 N/mm²

 

Calcestruzzo ordinario di classe C40/50con fck = 40 N/mm²

fck/ y_m= (40 N/mm²) / 1,15 = 22,86 N/mm²

 

Dimnesionamento trave

Ipotizzo una base di 35 cm per la trave, ottengo un’altezza di 68,19 cm che arrotonderò a 75 cm .

Aggiungo il carico della trave e verifico il dimensionamento.

Carico trave= 5,97 KN/m = Q = 52,455 + 5,97 = 58,425 KN/m

Ricalcolato il peso con il foglio Excel ho la conferma che la trave da me scelta è corretta.

TRAVE 35X75 CM

 

 

5_STRUTTURA RETICOLARE SPAZIALE

Disegno ed analisi di uina struttura reticolare spaziale con AUTOCAD e SAP2000.

1_AUTOCAD

 

1.1  Il primo passo per la realizzazione di questa esercitazione è la creazione, nel menù Layer di Autocad, di un nuovo Layer che chiamerò ASTE, che includerà tutti gli elementi della mia struttura. Una volta importato in SAP assegnerò ad ogni asta la funzione di FRAMES.

1.2  Disegno in Autocad la mia piastre reticolare spaziale di forma cubica con dimensioni (2mx2mx 2m). Parto dal punto di origine degli assi 0,0,0 in modo che una volta importato il disegno su SAP non avrò problemi ad individuarlo. Disegno in 2D le prime 4 aste del modulo, 3 ortogonali ed 1 diagonale,  con un’unica polilinea.

1.3  Mi sposto sul piano 3D utilizzando il comando Visualizza - Punti di vista 3D – SO assonometrico.

1.4  Ruoto la polilinea con il comando Ruota 3D, impostando come asse  di rotazione l’asse X e come angolo di rotazione un angolo di 90°.

1.5  Per disegnare in serie altri moduli della trave reticolare, seleziono la mia polilinea ed attraverso il comando Array/Serie imposto una serie di 4 colonne ed una riga, ciascuna ad una distanza di 2m dall’altra.

1.6  Il risultato ottenuto è una trave reticolare priva dell’ultima asta verticale, che aggiungerò in seguito con il comando Polilinea 3D.

1.7  Avendo completato la mia trave, posso ora passare alla costruzione degli altri moduli reticolari, utilizzando il comando Array/Serie impostando una serie di 7 righe ed una colonna, ciascuna ad una distanza di 2m dall’altra.

 

1.8  Ottengo cosi una travatura spaziale incompleta. Infatti ogni modulo è privo delle aste laterali. Attraverso il comando Polilinea 3D, andrò a disegnarmi un una polilinea di 3 aste che con il comando Array/Serie estenderò a tutta la struttura impostando una serie di 6 righe e 5 colonne, ciascuna ad una distanza di 2m dall’altra.

1.9  La struttura è ancora incompleta. Mancano le diagonali superiori ed inferiori di ogni modulo, che disegnerò con il comando Polilinea 3D ed estenderò a tutta la struttura con il comando Array/Serie, con una serie di 6 righe e 4 colonne, ciascuna ad una distanza di 2m dall’altra.

1.10  Il risultato finale è una struttura reticolare spaziale asimmetrica. L’ultimo passaggio  prima di esporta il file Dxf su SAP è l’esplosione di tutte le polilinea della struttura attraverso il passaggio  Esplodi.

 

2_SAP2000

2.1  Assegno al Layer Aste la funzione Frames.

2.2  Definisco i vincoli esterni della struttura selezionando i 4 vertici inferiori ed assegnando 4 cerniere, attraverso il comando Assign – Joint – Restraints.

2.3  Definisco i vincoli interni. Tutte le aste che compongono la struttura sono incernierate tra di loro e non incastrate. Seleziono tutte le aste della struttura con Select – All  ed attraverso il comando Assign - Frame - Partial fixity - Assign frame releases impongo il rilascio dei momenti all’inizio ed alla fine delle aste selezionate in precedenza.

2.4  Definisco il materiale della struttura. Attraverso il comando Define- Material- New material e creo il materiale Acciaio.

2.5  Defisco la sezione del materiale. Con il comando Define- Section properties- Frame section scelgo la sezione Pipe che andrò a rinominare Tubolare, assegnando il materiale acciaio.

2.6  Con Assign- Frame- Frame section  assegno a tutte le aste della struttura  il profilo stabilito

2.7  Assegno i carichi alla struttura. Definisco un carico che chiamerò Forza Concentrata con il comando Define - Load pattern. Per facilitare vado settare il Set Display Options, selezionado la casella Frames – Frames Not in View e deselezionando Joints – Invisible. Spostando la vista in modalità XY, riuscirò più facilmente a selezionare i nodi superiori su cui applicare un carico verticale di 40 KN.

2.8  La struttura è ora completa dei carichi. Posso cosi lanciare l’analisi.

 

2.9  Per capire qual è l’asta più sollecitata, devo selezionare il comando Display - Show Tables – Elements Output, ottenendo cosi una tabella con tutte le caratteristiche e le sollecitazione delle varie aste che compongono la mia struttura. Dopo aver individuato l’asta più sollecitata a trazione e quella più sollecitata a compressione, procedo con il progetto e la verifica.

Risultati SAP:

N_max compressione= 307,254 KN  Asta n° 137

N_max trazione= 258,934 KN  Asta n° 50

SFORZO MASSIMO A COMPRESSIONE

L'asta della struttura più sollecitata a compressione è la numero 137, su cui agisce un N di 307,254 KN.

Per il progetto della trave scelgo un acciaio S355 =

A = N / fd= 307,254 KN / (355/1,05) = 307254 N / (338,095 N/mmq) = 908,78 mmq = 9,09 cmq

fd = fy/γm = 338,095 N/mmq

fy = resistenza a snervamento

γm = coefficiente di sicurezza

Seleziono un profilo di dimensioni 114,3x3,6 mm con una sezione pari a 12,5 cmq.

Per concludere il progetto della trave bisognerà verificare se la sezione è in grado di sopportare lo sforzo di compressione, attraverso la formula del carico critico euleriano, fenomeno che avviene se un elemento strutturale, soggetto a compressione, si inflette e sbanda a causa della sua snellezza.

Carico critico euleriano:

Pcr= (π² x E x J_min)/l₀²

E= Modulo di elasticità

J_min= momento di inerzia minimo della sezione risultante dal profilario

l₀= lunghezza libera di inflessione, che dipende dal materiale, dai vincoli e dalla sezione, in questo caso essendo un'asta doppiamente incernierata la lunghezza libera di inflessione è uguale alla  lunghezza stessa dell'asta.

Pcr= (3,14 x 3,14 x 210000N/mmq x 1920000 mm⁴)/ 2828 mm x 2828 mm = 497,073 KN

497,073 KN > 307,25 KN

Il profilo scelto è verificato.

SFORZO MASSIMO A TRAZIONE

L'asta della struttura più sollecitata a compressione è la numero 50, su cui agisce un N di 258,934 KN.

Per il progetto della trave scelgo un acciaio S355 =

A = N / fd= 258,934 KN / (355/1,05) = 258934 N / (338,095 N/mmq) = 766 mmq = 7,66 cmq

fd = fy/γm = 338,095 N/mmq

fy = resistenza a snervamento

γm = coefficiente di sicurezza

 

Seleziono un profilo di dimensioni 114,3x3,6 mm con una sezione pari a 12,5 cmq.

Verifica a resistenza

Bisognerà verificare se il rapporto tra lo sforzo normale e l’area del nuovo profilo risulterà essere inferiore ad fd:

258934 N/1250 mmq = 207,147 N/mmq < 338,095 N/mmq

Il profilo scelto è verificato.

 

6_RIPARTIZIONE FORZE SISMICHE

 

(esercitazione svolta in collaborazione con Edoardo Capuzzo Dolcetta)

INTRO

In questa esercitazione andremo a vedere come le forze sismiche vengono ripartite su una struttura di un piano costituita da otto controventi.

 

L’impalcato riportato è costituito da 12 pilastri (20x40cm) in calcestruzzo armato, disposti e orientati così da avere il momento di inerzia maggiore della sezione del pilastro in asse con la trave che ha una luce maggiore e quindi con un momento più grande. 

STEP#1- calcolo delle rigidezze traslanti dei controventi dell'edificio

Tutti i controventi sonoShear-typee quindi la loro rigidezza è:

 

Kt= 12 xEx J /h³

 

E = modulo di Young che per il c.a. E = 21000 N/mmq

h = altezza del telaio, scegliamo h = 3,20 m

J = momento di inerzia

Attenzione!Bisogna tener sempre presente che in un singolo telaio possiamo avere pilastri con diversi momenti d’inerzia.

 

 

 

J = b x h³ /12 = (20 x (40)³ ) cm/12 = 106667.00 cm⁴

J= b J= b x h³ /12 = (40 x (20)³ ) cm/12 =  26667.00 cm⁴

Adesso inseriamo nel nostro bel foglio excel i dati relativi a ciascun telaio e ne calcoliamo la rigidezza:

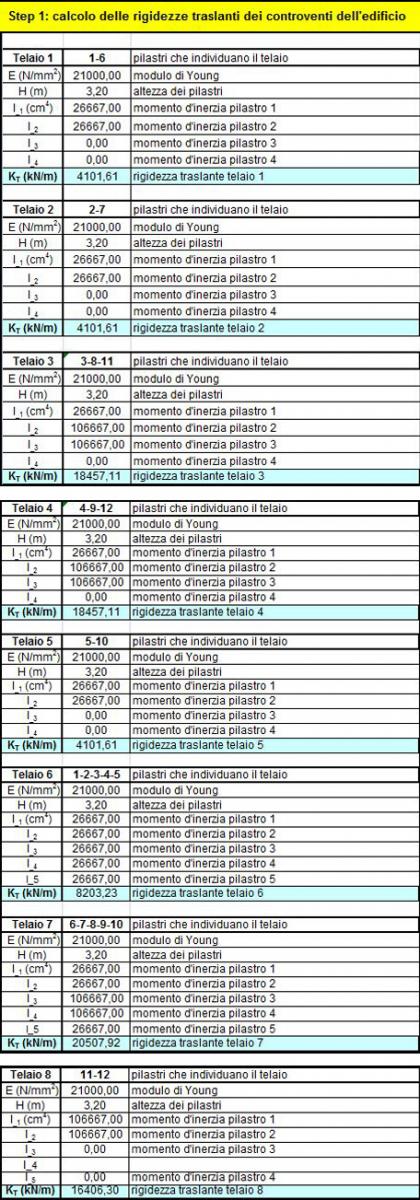
Step#2: tabella sinottica controventi e distanze

La tabella sottostante ci aiuta a ricapitolare quanto fatto finora:

-       ci riporta le rigidezze di ogni singolo telaio

-       mostra le relative distanze dal punto chiamato O (origine del sistema)

 

Step#3: calcolo del centro di massa

Ora il foglio excel ci aiuta a trovare le coordinate X_G  e Y_G del centro di massa, a partire dalle due aree (A₁ e A₂) che formano il nostro impalcato

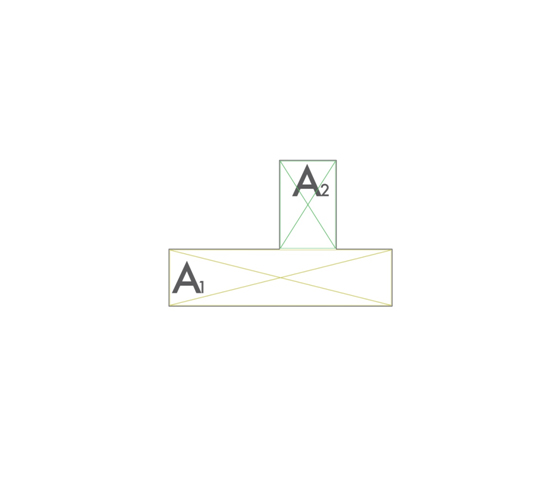
excel trova X_G e Y_G  in questo modo:         

X_G =( A₁ xX_G1+ A₂ xX_G2) / (A₁+ A₂)

Y_G  =( A₁ xY_G1+ A₂ xY_G2) / (A₁+ A₂)

Otteniamo:          X_G = 7,85 m                 Y_G  = 2,96 m

Step#4: calcolo del centro di rigidezze e delle rigidezze globali

Excel adesso ci aiuta a sommare le rigidezze dei singoli telai riportate nella tabella dello step 2 per ottenere le rigidezze totali.

Kx tot =  rigidezza totale orizzontale 

Ky tot = rigidezza totale verticale

Passiamo adesso a calcolare le coordinate del centro delle rigidezze C.

Sotto l’azione della forza sismica, l’impalcato tenderà a ruotare proprio intorno a questo punto C.

Xc = (K_y1 x d_y1 + K_y2 x d_y2+ K_y3 x d_y3 + K_y4 x d_y4 )/ (Ky tot)

Yc = (K_x1 x d_x1 + K_x2 x d_x2+ K_y3 x d_x3 + K_y4 x d_x4 )/ (Ky tot)   d = distanza dei controventi dal centro delle rigidezze

Otteniamo:          X_C = 10,68 m                 Y_C  = 7,00 m

La rigidezza torsionale verrà quindi calcolata:    Kϕ= Ʃ_i k_i dd_i²

STEP#5: analisi dei carichi sismici

La forza sismica è data dal prodotto della massa dell’edificio per l’accelerazione di trascinamento del suolo quando vibra. Il valore di questa “vibrazione” (a) ci è dato dalla normativa e corrisponde ad una frazione dell’accelerazione di gravità (g).

Quindi:

Fsismica = m a

ma    a = c g      dove c < 1 (coefficiente dato dalla normativa)

quindi      Fsismica = m c g = c (mg)

dove mg = Peso  ---  Fsismica = c P

Attenzione!Si evince che la forza sismica è una frazione della forza peso àun elemento molto pesante sarà molto vulnerabile al sisma! (al contrario, più un edificio è “leggero” e meno sarà vulnerabile) 

Adesso inseriamo i carichi strutturali, permanenti e accidentali per un’abitazione ad uso civile

(q_a = 2.00) e ci calcoliamo il peso della nostra struttura.

P_struttura = G + ψQ    dove G = carico totale permanente = (qs + qp) Atot

ψ= coefficiente di contemporaneità (da normativa) che diminuisce il carico accidentale.

Q = carico totale accidentale = qa Atot

STEP#6 - 7: ripartizione forza sismica lungo x ed y

Gli step 6 e 7 ci permettono di calcolare la forza ripartita su ogni controvento oltre che lo spostamento e la rotazione dell'impalcato.

Però prima dobbiamo ricordarci che il sisma è un’azione aleatoria e di conseguenza ci è sempre ignota la direzione lungo la quale esso si verificherà. Così le norme ci impongono di verificare la ripartizione delle forze sismiche almeno in due direzioni ortogonali fra loro (nel nostro caso proprio x ed y).

Il momento torcente, che farà ruotare il nostro impalcato, si verifica se i controventi non hanno tutti le stesse rigidezze o se la forza non agisce lungo l’asse delle rigidezze.

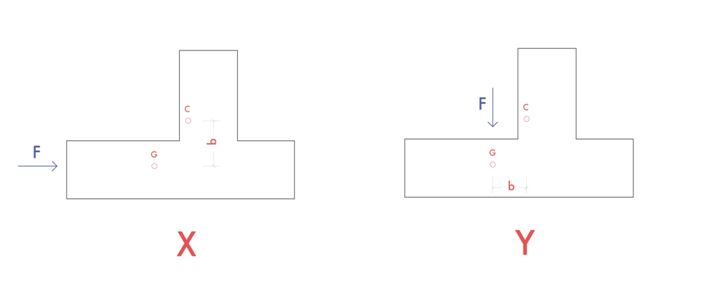
Il momento torcente è il risultato della forza sismica (applicata sul centro di massa G) per il braccio (b, nel disegno) dato dalla distanza del punto C dal punto G.

La traslazione orizzontale vale:           U_o = F_sismica/K_otot

La traslazione verticale vale:                  V_o = F_sismica/K_vtot

La rotazione invece vale:                       ϕ= M/K_ϕtot

Infine calcoliamo come la forza sismica viene ripartita nei singoli controventi.

Le reazioni vincolari si determinano:

Orizzontale           R_io = K_io (Uo+φd_io)

Verticale                    R_iv = K_iv (φd_iv)

Mt = F (Yc - Yg) = F xb
Mt = F (Xc - Xg) = Ff xg