TRAVATURE RETICOLARI

Per travature reticolari, intendiamo una struttura formata da varie aste, tutte appartenenti ad un unico piano, vincolate tra di loro tramite cerniere interne.

1)VERIFICA ISOSTATICITA'                                                                                                         Per verificare l'isostaticità della travatura reticolare deve essere valida la condizione L=V, dove con L, intendiamo i gradi di libertà  delle aste, ogni asta ne ha tre, e con V, la sommatoria dei vincoli interni ed esterni.

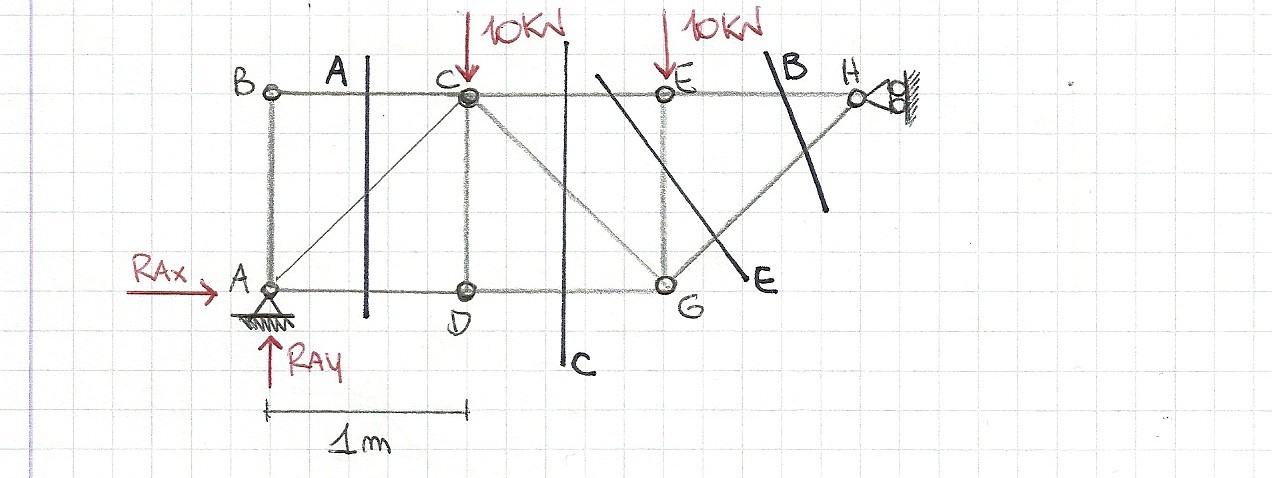
L=V      L=11X3=33                                                            

V=Ve+Vi    Ve=2+1H=3  Vi=2(n-1)                                   

V=3+30=33                                                                         

L=V

2) CALCOLO DELLE REAZIONI VINCOLARI

A questo punto si procede esaminando la reazione dei vincoli, in modo che la sommatoria delle forze orizzontali, verticali e la sommatoria dei momenti sia uguale a zero. Questa condizione deve essere soddisfatta affinchè la travatura si trovi in equilibrio.

3) SVOLGIMENTO

Per risolvere le travature reticolari, possiamo utilizzare due metodi:

- METODO DELLE SEZIONI DI RITTER

-METODO DI EQUILIBRIO AI NODI

METODO DELLE SEZIONI DI RITTER

Questo metodo ci permette facilmente di conoscere le reazioni di un'asta qualsiasi, in modo autonomo, così senza obbligatoriamente risolvere l'intera struttura.

Si risolve operando una sezione di Ritter, in modo che tagli contemporaneamente minimo tre aste, di cui due s'incontrino nello stesso punto; quest'ultimo può essere proprio o improprio.

SEZIONE A

SEZIONE B

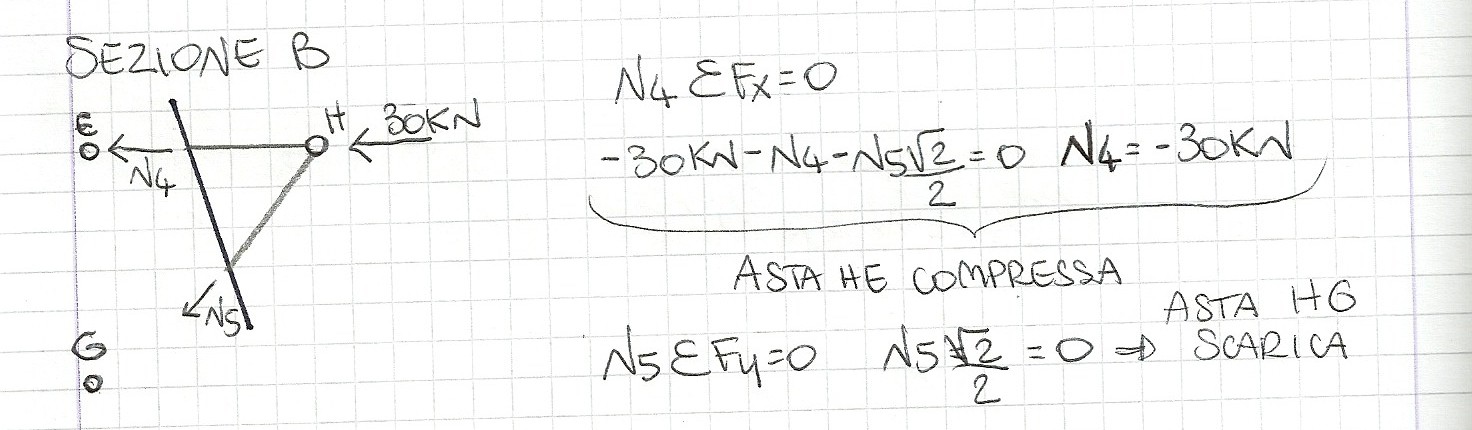
SEZIONE C

SEZIONE D

SEZIONE E

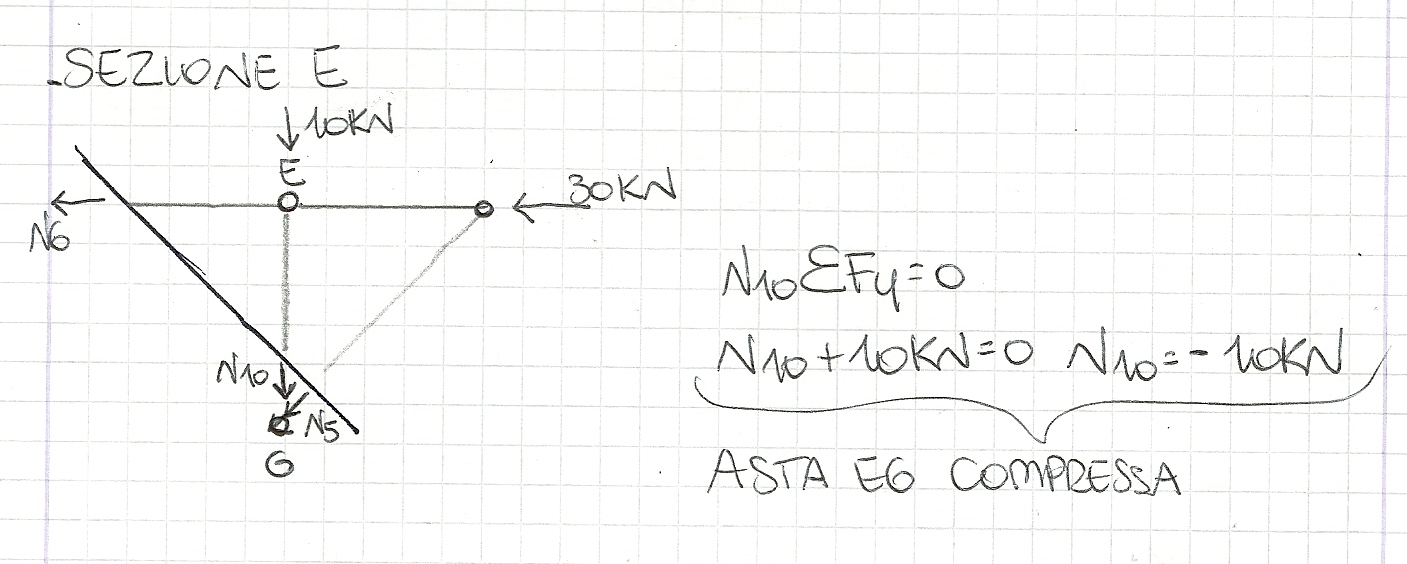
Avendo risolto le reazioni di tutte le aste, abbiamo verificato che quest'ultime sono soggette solo a sforzo normale e quindi le possiamo distinguere in TIRANTI, quando lo sforzo normale è di trazione, l'asta è tesa, e PUNTONI, quando lo sforzo normale è di compressione quindi l'asta è compressa.

METODO DEI NODI

Si applica di solito su travature reticolari, dove si sia già verificato l'equilibrio, e per questo motivo deve risultare in equilibrio ogni suo nodo, cioè le equazioni R=0 e M=0, con il quale indichiamo le risultanti delle reazioni e dei momenti, devono essere verificate per ogni singolo nodo.

Verifica dei grafici con Saap