Esercitazioni

Analisi di una struttura reticolare simmetrica

Innanzitutto, per poter analizare una struttura come una struttura reticolare bisogna considerare le aste della trave puramente tese o compresse, quindi non bisogna considerare il peso proprio della struttura che causerebbe momenti e sforzi di taglio, ed inoltre ogni elemento è incernierato l'uno all'altro permettendo il momento ed i carichi esterni siano puntuali su una delle cerniere. 

Adesso prendiamo in esempio, una trave reticolare simmetrica, verificandola con il sistema delle sezioni di Ritter. Questa struttura si definisce simmetrica sotto due punti due vista, sia per la geometria, sia per la ripartizione dei carichi esterni.

Come si può vedere dalla struttura qui al lato quindi la struttura è perfettamente simmetrica, sia nella geometria che nella ripartizione dei carichi esterni.

 

 

 

Per prima cosa si verifica l'isostaticità della trave attraverso la verifica dei gradi di vincolo e di libertà.

Per definizione una struttura isostatica una struttura nel quale i gradi di vincolo sono pari ai gradi di libertà, nel caso fosseri minori la struttura si definisce labile, nel caso fossero maggiori la struttura si definisce iperstatica.

Quindi:

V = L  e  V = Vi + Ve     poichè i gradi di vincolo sono la somma dei vincoli interni ed esterni

Ve = 2 +1 = 3   2 sono i vincoli dati dalla cerniera, mentre uno è il contributo del carrello

 Vi  viene calcolato in ogni nodo attraverso la formula 2(n-1) dove n è il numero dei corpi che si incontrano nel nodo, quindi:

nei nodi A,H    = 2(2-1) = 2 x 2 = 4

nei nodi B,G    = 2(3-1) = 4 x 2 = 8

nei nodi D,C,E = 2(4-1) = 6 x 3 = 18

quindi, i vincoli interni sono 18+8+4 = 30, i vincoli esterni sono 3, quindi V= 33

I gradi di libertà si calcola moltiplicando il numero dei corpi per 3, quindi 11x3 = 33

Quindi, V = L   

La struttura è isostatica.

Data l'isostaticità della struttura allora si possono ricavare le reazioni vincolare:

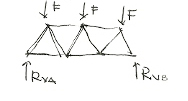Rua, è uguale a zero, visto che non esistono altre forze orizzontali, e data la simmetria della struttura, come detto prima, allora Rva e Rvb sono uguali, ripartendosi equamenti il carico 3F.

 

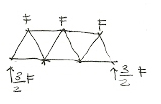
Le reazioni vincolari della struttura.

Per calcolare le azioni di contatto, si può utilizzare il metodo delle sezioni di Ritter. Questo metodo prevede un taglio virtuale di 3 aste che non convergono tutte nello stesso nodo. Quindi, data la simmetrica, come più volte detto, della struttura, si può analizzare solamente metà trave, data la specularità delle forze.

Come si vede dalla figura sono stati applicati 3 tagli, in modo da prendere 3 aste non convergenti sullo stesso nodo.

 

 

Analisi del primo taglio

Attraverso la risultante dei momenti in C, si può ricavare che N1= -2F, quindi l' asta è compressa.

Invece, grazie alla risultante dei momenti in B, si può ricavare che N3 = 3/2F, quindi l asta è tesa.

L'equilibrio alla traslazione verticale invece, fa ricavare che N2= F√2/2, quindi l'asta è  è tesa.

N1 e N3 erano facilmente prevedibili, dato che in una trave reticolare semplice, il corrente superiore è sempre compresso, mentre quello inferiore è sempre teso.

Analisi del secondo taglio

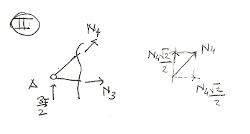Facendo l'equilibrio alla traslazione verticale e avendo scomposto N4 nelle sue componenti orizzontali e verticali, si può ricavare quest'ultima, la quale è uguale a          -3/2F√2. Quindi l'asta è compressa.

 

 

Analisi del terzo taglio

Dall'equilibrio dei momenti in D si ricava che N5 è 3/2F, quindi l'asta è tesa.

Dall'equilibrio alla traslazine verticale, si ricava che N6 è uguale a 5F√2/2, anche quest'asta è tesa.

 

 

 

In questo schema si possono vedere gli sforzi normali presenti sulla trave, con i rispettivi valori espressi in kN. In giallo sono evidenziate la aste tese, mentre soon state lasciate a matita quelle compresse.

 

 

Analisi di una struttura reticolare asimmetrica

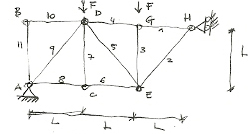
 Seguo i passaggi di verifica dell'esercizio precedente, ossia controllo per prima cosa che la struttura è isostatica.

Quindi V deve essere uguale a L ed in questo caso sono:

L = 3x11 =33

V_e = 3

V_i = 2(n-1), quindi:

nel nodo A = 2(3-1)=4

nel nodo B = 2(2-1)=2

nel nodo C = 2(3-1)=4

nel nodo D = 2(5-1)=8

nel nodo E = 2(4-1)=6

nel nodo G = 2(3-1)=4

nel nodo H = 2(3-1)=2

Quidni V_i  è uguale a 30 e V= 30 +3=33 = L

La struttura è isostatica.

Calcolo delle reazioni vincolari

Per calcolare Ruh, basta fare l'equilibrio dei momenti in A, trovato Ruh, basta fare l'equilibro alla traslazione orizzontale e verticale per trovarsi le reazioni vincolari in A.

 

 

Quindi, si ha che:

 

 

 

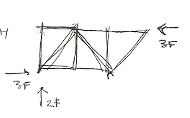
A questo, attraverso il metodo dei nodi vengono calcolate le azioni di contatto. Questo modo isola ogni nodo e le forze agenti su questi. 

Nodo H

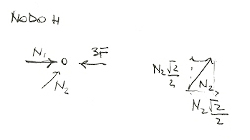Scomponendo la forza N2  nelle sue componenti orizzontali e verticali, si ricava facilmente attraverso gli equilibri alla traslazione verticale ed orizzontale che N2=0, e che l'asta due quindi è scarica, e che N1 = 3F , quindi l'asta è compressa.

Da notare che nel metodo dei nodi, le frecce che nei diagrammi rappresentanole forze che l' asta applica sul nodo, quindi si ha una rappresentazione grafica leggermente diversa rispetto al metodo di Ritter.

Nodo G

Da qui sono facilmente ricavabili N3 (F, l'asta è compressa) e N4 (-3F, anche quest'asta è compressa).

 

 

Nodo C

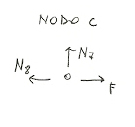In questo caso è molto semplice dedurre che l'asta 7 sia scarica è che N8 sia uguale a -F, quindi compressa.

 

 

 

Nodo A

 Scomponendo la forza N9 nelle sue componenti orizzontali, anche qui è facile trovare gli sforzi assiali delle aste:

N9 = -2F√2 (l'asta è compressa)

N8 = -F (anche quest'asta è compressa)

 

Sforzo normale della trave:

In rosso sono evidenziate le aste compresse e blu quelle tese. Ben quattro aste sono scariche.

 

Qui invece vengono mostrati anche i valori (calcolati attraverso l'utilizzo di SAP2000)

 

 

 

 

 

 

 

 

 

 

 

Progetto di una trave inflessa

 

Dato l'impalcato rappresentato nell'immagine seguente, verrà studiata e progettata la trave maggiormente sollecitata (quella indicata) in tre diverse tecnologie per confrontarle e studiarle: legno, acciaio e calcestruzzo armato.

 

 

1 | Legno

 

 

 

 

 

 

 

Nel disegno a fianco si può vedere la stratigrafia della struttura orizzontale lignea con i suoi spessori ed i suoi diversi componenti.

 

La progettazione della trave si divide innanzitutto nella scelta delle tecnologie da usare (come si vede dall'immagine precedente) e nel calcolo della trave.

Per prima verrà prima dimensionato un travicello del solaio, verificato, ed in seguito verrà dimensionata la trave, ed anch' essa verificata.

 

Progetto a flessione di un travicello in legno

 

Analisi dei carichi agenti su una porzione di un mq del solaio 

 

Per il calcolo dei carichi, bisogna suddividere in carico strutturale, permanente e accidentale. Lo strutturale è tutto ciò che è portante, permanente è tutto ciò è non strutturale, e accidentale sono dei carichi legati alla funzione degli ambienti.

Il carico accidentale è un valore tabellato dato dalla normativa a seconda delle funzioni, mentre quello strutturale e quello permanente vanni ricavati attraverso lo studio delle tecnologie usate e dalla morfologia dell'edificio.

Per esempio nel carico permanente vanno calcolate le densità superificiali moltiplicando il peso specifico dei singoli materiali per i loro spessori.

 

Calcolo Carico Strutturale

 

Tavolato 0,03 m * 490 kg/mc = 14,7 kg/mq

 

Totale qs: 14,7 kg/mq = 0,15 kN/mq

 

Calcolo Carico Permanente

 

Massetto alleggerito 0,07 m * 480 kg/mc = 33,6 kg/mq

Malta allettamento 0,02 m * 1800 kg/mc = 36 kg/mq

Pavimento in cotto 0,02 m * 2300 kg/mc = 46 kg/mq

Impianti 50 kg/mq

Tramezzi 100 kg/mq

 

Totale qp: 265,6 kg/mq = 2,65 kN/mq

 

Calcolo Carico Accidentale

 

Costruzione per civile abitazione 2 kN/mq

 

Somma dei carichi agenti su un'area di 1mq 4,80 kN/mq

 

Calcolato il carico totale agente su un'area di solaio, converto il peso a metro quadro in densità lineare, la quale corrisponde al carico agente sul filo della trave. Quindi basta moltiplicare la densità superificiale per l'interasse (1m), quindi:

4,80 kN/mq * 1 m = 4,80 kN

 

Calcolo del momento sul travicello

 

Una volta trovato il carico totale, per poter procedere al calcolo del momento bisogna inserire la luce (in questo caso 3,30 m), poichè è il fattore che influisce maggiormente sull'azione di contatto. Considerando il travetto come una trave appoggiata, sappiamo che il momento massimo è pari a ql²/8 in mezzeria, quindi avendo impostato il foglio excel con questi parametri , possiamo ricavare agilmente il momento massimo,

 

vale a dire 6,53 kNm

 

Calcolo resistenza flessionale di design

 

Lo step successivo è di calcolare la resistenza flessionale di design, per il legno bisogna tenere conto di più fattori legati anche alla normativa.

 

Fmk è la resistenza caratteristica a flessione ( 28 Mpa per il castagno), Kmod è un coefficiente correttivo che tiene conto dell’effetto, sui parametri di resistenza, sia della durata del carico sia dell’umidità della struttura (0,6 per i carichi permanenti su solai in legno massello), ed un fattore γm che è il coefficiente parziale di sicurezza relativo al materiale (per il legno massello 1,5).

 

Inserendo i dati nella tabella excel si ha che la resistenza di design fd è pari a 11,20 Mpa.

 

 

Calcolo altezza travicello

 

L'ultimo step consiste nel calcolare l'altezza della trave, ponendo una base come dato.

Sfruttando le proprietà di una sezione rettangolare , sappiamo che il modulo di resistenza flessionale Wx è ugulae bh²/6 (ricavato dal momento d'inerzia ) , e che è anche uguale al rapporto fra il momento massimo e la resistenza di design ( Wx = Mmax/ fd) , quindi uguagliando le due equazioni si può ricavare che:

 

h = (6*Wx *b)^1/2

 

Compilando il foglio excel si ha che l'altezza è 16,79 cm e la base 12 cm

Quindi il travicello avrà dimensioni 12x18 cm 

 

 

Verifica a flessione della trave in legno 

Per verificare la resistenza della trave viene considerato anche il peso proprio del travicello stesso, quindi il carico strutturale sarà:

 

Calcolo Carico Strutturale

 

Tavolato 0,03 m x 490 kg/mc = 14,7 kg/mq

Peso proprio (0,12m x 0,18m x 490 kg/mc )/ 1 m= 8,82 kg/mq

 

Totale qs: 26,52 kg/mq = 0,26 kN/mq

 

Quindi il carico totale diventa 4,91 kN/mq, e ripetendo il procedimento precedente abbiamo che l'altezza richiesta sarebbe 16,98 cm, quindi il travicello è verificato.

 

 

 

Progetto a flessione della trave in legno

Analisi dei carichi agenti su una porzione di un mq del solaio

 

Il peso agente sulla porzione unitaria del solaio è uguale a quella a calcolata per la verifica del travicello, quindi 4,91 kN/mq. 

Analisi dei carichi agenti sulla trave

 

Per poter calcolare il carico agente sulla trave basta moltiplicare il peso al mq del solaio per l'interasse, che per la trave è 3,00 m, quindi 

4,91 kN/mq x 3,00 = 14,73 kN/m 

Calcolo del momento sulla trave

 

Il momento, grazie al foglio excel risulta come dettto precedentemente facilmente calcolabile, ponendo sempre la trave come doppiamente appoggiata, possiamo calcolare l'azione di contatto che equivale a ql²/8 ( e la luce è 5m). Quindi,

M = 46,03 kN/mq

 

Calcolo resistenza flessionale di design

 

La resistenza flessionale di design è la medesima visto che il materiale è lo stesso, quindi,

fd =11,20 Mpa.

 

Calcolo altezza trave

 

Con le stesse relazioni con cui si è trovata l'altezza utile del travicello, si calcola quella della trave, ponendo però la base non 12 cm ma 20 cm. L'altezza quindi risulta 34,52 cm, quindi la trave utilizzata sarà 20cm x 35cm.

 

Verifica a flessione della trave 

Per verificare la resistenza del travicello viene considerato anche il peso proprio del travicello stesso, quindi il carico strutturale sarà:

 

Calcolo Carico Strutturale

 

Peso solaio strutturale 0,26 kN/mq

Peso proprio (0,20m x 0,35m x 490 kg/mc )/ 3 m= 11,43 kg/mq = 0,11 kN/mq

 

Carico Totale Strutturale 0,37 kN/mq

 

Verifica altezza trave 

Utilizzando i nuovi carichi, l'altezza della trave risulta essere 34,91 cm, quindi minore della trave che è 35 cm. Dato il poco scarto tra le due altezze sarebbe auspicabile una trave più alta che possa far fronte in modo migliore a carichi imprevisti.

 

 

 

 

 

 

2| Acciaio

 Sempre analizzando lo stesso impalcato, però cambiando tecnologia calcolo l'altezza del solaio e della trave.

 

 

Nella figura si vede il solaio in lamiera grecata con getto in calcestruzzo. Il pavimento ed il massetto sono i medesimi del solaio in legno, però invece di essere a vista nell'intradosso ha un controsoffitto.

L'altezza della lamiera e del getto è stato calcolato con delle tabelle di dimensionamenti di massima in base alla luce della lamiera.

 

 

 

 

Con questa tabella è stato dimensionato e ricavato il peso del solaio con la lamiera grecata. In basso si vede la sezione della lamiera grecata e la tipologia.

 

 

 

 

 

 

 

 

 

 

 

Carico Strutturale

Lamiera grecata con getto di cls 1,5 kN/mq

 

Carico Permanente

 

Massetto alleggerito 0,07 m * 480 kg/mc = 33,6 kg/mq

Malta allettamento 0,02 m * 1800 kg/mc = 36 kg/mq

Pavimento in cotto 0,02 m * 2300 kg/mc = 46 kg/mq

Impianti 50 kg/mq

Tramezzi 100 kg/mq

Controsoffitto 10 kg/mq

 

Totale qp: 275,6 kg/mq = 2,75 kN/mq

 

Calcolo Carico Accidentale

 

Costruzione per civile abitazione 2 kN/mq

 

Somma dei carichi agenti su un'area di 1mq 6,25 kN/mq

 

Calcolato il carico totale agente su un'area di solaio, converto il peso a metro quadro in densità lineare, la quale corrisponde al carico agente sul filo della trave. Quindi basta moltiplicare la densità superificiale per l'interasse (3m), quindi:

6,25 kN/mq * 3 m = 18,75 kN

 

Calcolo del momento sulla trave

 

Una volta trovato il carico totale, per poter procedere al calcolo del momento bisogna inserire la luce (in questo caso 5 m), poichè è il fattore che influisce maggiormente sull'azione di contatto. Considerando il travetto come una trave appoggiata, sappiamo che il momento massimo è pari a ql²/8 in mezzeria, quindi avendo impostato il foglio excel con questi parametri , possiamo ricavare agilmente il momento massimo,

vale a dire 58,59 kNm

 

Calcolo resistenza flessionale di design

 

La resistenza flessionale di design nell'acciaio è semplicemente la resistenza caratteristica del materiale diviso per γm che è il coefficiente parziale di sicurezza relativo al materiale (per l'acciaio da carpenteria è 1,05).

La resistenza caratteristica, invece, avendo usato un acciaio Fe 360/S235 è pari a 235 Mpa, quindi:

fd = 223,81 Mpa

 

 

Calcolo altezza sezione della trave

 

Il calcolo della sezione della trave in acciaio è lievemente diverso rispetto a quello della trave in legno. Il modulo di resistenza Wx è sempre pari a Mmax/ fd, e non essendo la sezione quadrata il modulo d'inerzia sarà completamente differente, perciò Wx va verificato sul sagomario delle travi IPE, il quale riporta tutte le caratteristiche geometriche di ogni sezione. Quindi.

Wx = 261,80 cmc

 

 

 

 

 

 

 

 

 

Quindi dato il valore di Wx scelgo una trave IPE 240, il quale modulo di resistenza è 324 cmc, ampiamente sopra il valore di progetto.

 

 

Verifica a flessione della trave in acciaio

 

Per verificare la resistenza della trave viene considerato anche il peso proprio della trave stessa, quindi il carico strutturale sarà:

 

Lamiera grecata con getto di cls 1,5 kN/mq

Peso proprio trave 30,7 kg/m x 1/3m = 10,23 kg/mq = 0,1 kN/mq

 

Totale qs: 1,6 kN/mq

 

 

Verifica sezione

 

Utilizzando i nuovi carichi, l'altezza Wx risulta essere 265,99 cmc, quindi ancora molto minore rispetto al valore della trave data, che è 324 cmc. La trave è verificata.

 

 

 

 

 

 

 

   3| Calcestruzzo

 

 

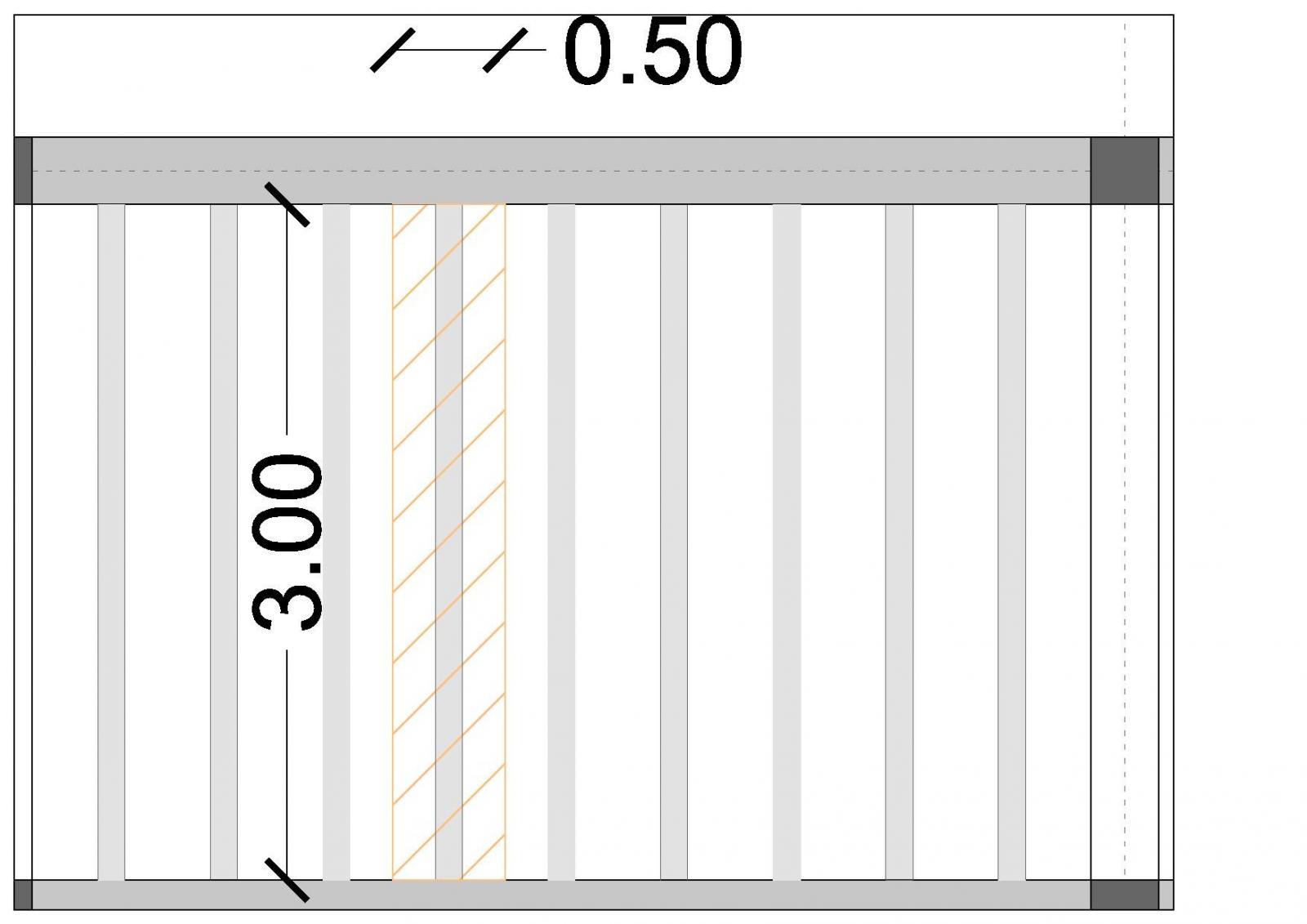
 In questa figura si può notare come il passo dei travetti sul solaio, ossia 50 cm, e la luce, 3,00m

 

 La stratigrafia è simile a quella dei casi precedenti, ossia, la parte strutturale è diversa, quindi un solaio in laterocemento, mentre tutta la parte superiore è identica ai casi sopracitati. 

 

 

 

 

 

 

 

 

 

 

 

 

Progetto a flessione di un travetto in cls

 

Analisi dei carichi agenti su una porzione di un mq del solaio

 

Carico strutturale

Caldana 0,04 m x 2400 kg/mc = 96 kg/mq = 0,96 kN/mq

 

Carico Permanente

 

Massetto alleggerito 0,07 m x 480 kg/mc = 33,6 kg/mq

Malta allettamento 0,02 m x 1800 kg/mc = 36 kg/mq

Pavimento in cotto 0,02 m x 2300 kg/mc = 46 kg/mq

intonaco 0,03 m x 100 kg/mc = 3 kg/mq

Impianti 50 kg/mq

Tramezzi 100 kg/mq

Pignatte 66,4 Kg/mq

 

 

Totale qp: 332 kg/mq = 3,30 kN/mq

 

Calcolo Carico Accidentale

 

Costruzione per civile abitazione 2 kN/mq

 

Somma dei carichi agenti su un'area di 1mq 6,26 kN/mq

 

 

 

 

 

Calcolo resistenza di design del cls

 

La resistenza di design del calcestruzzo si trova mediante la riduzione della resistenza caratteristica. Infatti data la poca affidabilità del materiale vi sono coefficienti di riduzione molto alti, infatti

 

fcd = αα fcd/ɣ

dove αα = 0,85e ɣ è 1,6

 

 

Quindi usando un calcestruzzo di classe C 30/37 (dove 30 MPa è la resistenza caratteristica) si avrà che,

fcd = 17,14 Mpa

 

 

 

 

Calcolo resistenza di design dell'acciaio

 

Per l'armatura vale lo stesso discorso fatto per l'esercizione del solaio in acciaio, quindi si divide la resistenza caratteristica per un fattore riduttivo, che per l'acciaio d'armatura è di 1,15. Quindi usando un'acciaio B 450 C

(l'unico usabile in zona sismica) si avrà che

 

fyd = 391,30 Mpa

 

 

 

 

Calcolo altezza utile del travetto

 

Per calcolare l'altezza utile del travetto ho bisogno dei valori r e α, che dipendenti dalle resistenza dei materiali, rappresentaono dei fattori di omogeneizzazione della sezione, e vengono calcolati direttamente dal foglio excel.

 

α = fc/fc+ff/n (dove n= Ef/Ec )

hu= r √M/b

 

Inoltre bisogna impostare una base, che solitamente per un travetto è di 10 cm, quindi l'altezza utile del travetto sarà di 12,02 cm, sommando 5 cm di copriferro (delta) la sezione sarà alta 17,02cm, ossia 20 cm.

 

Verifica a flessione di un travetto in cls

 

La differenza rispetto alla fase di progetto è la considerazione del peso proprio nei carichi strutturali, quindi:

 

Carico strutturale

 

Caldana 0,04 m x 2400 kg/mc = 96 kg/mq = 0,96 kN/mq

P.proprio (0,10m x 0,20m x 2400 kg/mc )/ 0,5 m= 96 kg/mq = 0,96 kN/mq

 

Carico strutturale totale 1,92 kN/mq

 

Somma dei carichi agenti su un'area di 1mq 7,22 kN/mq

 

Verifica Travetto

 

Utilizzando i nuovi carichi, l'altezza del travetto (compresa di copriferro) risulta essere 17,64 cm, quindi minore di 20cm. Il travetto è verificato.

 

 

Progetto a flessione della trave in cls

 

Analisi dei carichi agenti su una porzione di un mq del solaio

 

I carichi agenti sulla trave sono i medesimi di quelli calcolati per la verifica del travetto.

Quindi il carico totale è di 7,22 kN/mq

 

Progetto trave

 

Cambiando la grandezza della luce e dell'interasse (rispetto al travetto) si calcola nell'esatta maniera la grandezza della trave, quindi si avrà che la trave ha altezza di 36,54cm , quindi per correttezza di mmisure si adotta una trave 20x40 cm.

 

 

Verifica a flessione della trave in cls

 

Carico strutturale

 

Caldana 0,04 m x 2400 kg/mc = 96 kg/mq = 0,96 kN/mq

Travetti (0,10m x 0,20m x 2400 kg/mc )/ 0,5 m= 96 kg/mq = 0,96 kN/mq

P.proprio(0,20m x 0,40m x 2400 kg/mc )/ 3m = 64 kg/mq = 0,64 kN/mq

 

Totale qs: 2,56 kN/mq

 

Verifica trave

 

Ricalcolando con il foglio excel l'altezza della trave, risulta che la verifica da 39,66 come altezzaa totale, quindi la trave è verificata, dato che in fase di progetto era stata decisa alta 40 cm. Tuttavia, dato lo scarso margine della verifica, sarebbe auspicabile una sezione con altezza maggiore.

   

 

 

 

 

Analisi di una struttura reticolare spaziale in acciaio

 

Disegno della struttura su rhino

 Per rappresentare la travatura reticolare spaziale, mi sono avvalso di rhinoscript, un editor di testo che permette di parametrizzare e matematicizzare curve e superfici.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Per iniziare ho creato la griglia con le diagonali della parte inferiore della trave spaziale.In seguito ho disegnato la parte superiore della piastra

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Infine ho disegnato le aste centrali, creando un doppio ciclo for, è possibile far partire le aste (in questo caso linee, dato che dovranno essere importate su sap200) dai punti della grigla e congiungerli a quelli superiori. La sicurezza di questo metodo è che assicura il non ripetersi delle aste.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Prima di salvare in dwf, per esportare su sap2000, conviene cambiare layer agli oggetti, in questo caso le aste faranno parte del layer1

 

Analisi della struttura su SAP2000

 

Importo il dxf su sap, e comincio a mettere i vincoli alla struttura. Applico 4 cerniere ai quattro angoli della trave , applico i nodi alle estremità delle aste, rilasciando i momenti all'inizio e alla fine di queste.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Definisco una sezione (tubolare), un materiale (acciaio) e la assegno a tutte quante le aste.

 

 

I passi successivi riguardano i carichi, quindi, si definisce un carino, privo di peso proprio ( del moltiplicatore), la direzione (quindi l'asse ed il verso), la quantita del carico (i kN), ed i punti a cui assegnarli ( in questo caso tutti i nodi superiori della trave).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A questo punto basta far partire l'analisi, facendo attenzione a far partire soltanto i carichi concentrati precedentemente assegnati.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A questo punto il programma mi restituisce la deformata, le azioni di contatto, e i valori di queste, in questo caso ci interessano i valori massimi di N, per progettare le aste tese e compresse.

 

 

 

 

 

 

 

 

 

 

 

 

 La seguente tabella racconta i valori dell'asta più tesa e di quella più compressa.

 

 

  

Progetto delle aste compresse

 

La sollecitazione massima di compressione delle aste della travatura è uguale a 385,631 Kn. Quindi avendo lo sforzo normale e la resistenza di design ( per le aste ho scelto un acciaio Fe 510 S 355, quindi dividendo la resistenza caratteristica, 355 Mpa, per il coefficiente di sicurezza, 1.15, ricavo che la resistenza di design è 308,7 Mpa), posso ricavare l'area della sezione. Quindi

 

A = N/σ = 385631 N / 335 N/mmq = 1151,13 mmq = 11,51 cmq

 

 

Controllando il sagomario dei profili tubolari cavi, adotto una sezione di area 12,9 cmq con diamentro interno di 139 mm e spessore di 3 mm.

 

Verifica a resistenza

Bisogna verificare se il rapporto tra lo sforzo normale e l’area del nuovo profilo risulti essere inferiore ad fd:

385631 N/1290 mmq = 298,93 N/mmq < 335 N/mmq

La resistenza dell'asta è verificata.

 

Verifica carico critico

 

Per concludere il progetto della trave bisognerà verificare se la sezione è in grado di sopportare lo sforzo di compressione, attraverso la formula del carico critico euleriano, fenomeno che avviene se un elemento strutturale, soggetto a compressione, si inflette e sbanda a causa della sua snellezza. Quindi sapendo che il

carico eureliano corrisponde a

 

Pcr= (π² x E x Jmin)/l0² dove

 

E= Modulo di elasticità

Jmin= momento di inerzia minimo della sezione risultante dal profilario

l0= lunghezza libera di inflessione, che dipende dal materiale, dai vincoli e dalla sezione, in questo caso essendo un'asta doppiamente incernierata la lunghezza libera di inflessione è uguale alla lunghezza stessa dell'asta.

Pcr= (3,14 x 3,14 x 210000N/mmq x 3010000 mm4)/ (2828 mm)² = 779266 N = 779 kN

 

Quindi visto che il carico critico è maggiore rispetto allo sforzo normale allora l'asta è verificata.

 

verifica a snellezza:

 

λ = l0 /ϱ < 200

dove l0= luce libera di inflessione

ϱ = raggio di inerzia che in fase di verifica ricavo dal profilario

λ = 282,8 cm / 4,83 cm = 58,55 < 200, quindi è verificato

Progetto delle aste tese

 

La sollecitazione massima di tensione delle aste della travatura è uguale a 385,631 Kn. Quindi avendo lo sforzo normale e la resistenza di design ( per le aste ho scelto un acciaio Fe 510 S 355, quindi dividendo la resistenza caratteristica, 355 Mpa, per il coefficiente di sicurezza, 1.15, ricavo che la resistenza di design è 308,7 Mpa), posso ricavare l'area della sezione. Quindi

 

A = N/σ = 225325 N / 335 N/mmq = 672,61 mmq = 6,72 cmq

 

Controllando il sagomario dei profili tubolari cavi, adotto una sezione di area 8,10 cmq con diamentro interno di 889 mm e spessore di 3 mm.

 

Verifica a resistenza

Per le aste tese, invece basta la verifica a resistenza quindi verificare se il rapporto tra lo sforzo normale e l’area del nuovo profilo risulti essere inferiore ad fd:

225325 N/ 810 mmq = 278,17 N/mmq < 335 N/mmq

La resistenza dell'asta è verificata.