ESERCITAZIONI

STRUTTURA RETICOLARE SIMMETRICA - Risoluzione con il metodo delle sezioni di Ritter

 

Nella struttura in analisi le aste, in quanto componenti di una struttura reticolare, saranno sottoposte a soli sforzi normali. Applichiamo il metodo delle sezioni di Ritter per calcolare tali sforzi e stabilire se essi sono di trazione o compressione.

1.      Verifica dell’isostaticità

Dobbiamo accertarci che la struttura sia isostatica, quindi verificare che il numero dei gradi di vincolo (v) della struttura sia pari al numero dei gradi di libertà (l).

 

Da verificare                                                       v = l

 

I gradi di libertàl dipendono dal tipo e dal numero dei vincoli

l = num. aste x gradi di libertà

l = 11 x 3 = 33

I gradi di vincolo v sono pari alla somma dei gradi di vincolo esterni ed interni.

v = v_e + v_i

Gradi di vincolo esterni

I vincoli esterni sono una cerniera (2 gr. di vincolo) ed un carrello (1 gr. di vincolo), perciò

v_e = 2 + 1 = 3

Gradi di vincolo interni

I gradi di vincolo di una cerniera interna sono pari a 2 (n - 1)

con n = numero dei corpi, in questo caso numero di aste concorrenti nella singola cerniera.

 

Perciò considereremo i gradi di vincolo delle diverse cerniere interne raggruppando i nodi per numero di aste in essi concorrenti.

 

n = 2     nodi A, H      2(2 – 1) = 2 gradi di vincolo

n = 3     nodi B, G      2(3 – 1) = 4 gradi di vincolo

n = 4     nodi C, E, D   2(4 – 1) = 6 gradi di vincolo

v_i tot = 30

 

perciò  v = 3 + 30 = 33 = l à La struttura è isostatica.

 

Verifica  con metodo alternativo

Considero v_e + aste = 2 x num. nodi

3 + 11 = 2 x (7)

14 = 14 -> isostaticità verificata

 

2.      Reazioni vincolari

La simmetricità della struttura e dei carichi permette di avere importanti informazioni rispetto alle reazioni vincolari:

-          Le reazioni saranno simmetriche, V_A = V_H;

-          La reazione orizzontale della cerniera (O_A) sarà nulla in quanto il vincolo simmetricamente opposto è un carrello che in quanto tale non può produrre reazione orizzontale;

-          Le reazioni verticali in A ed H si spartiranno equamente il compito di contrastare la somma delle forze applicate esterne. Saranno perciò pari a 3F/2.

 

con F = 20 avremo V_A = V_H = 3F/ 2 = 30 KN

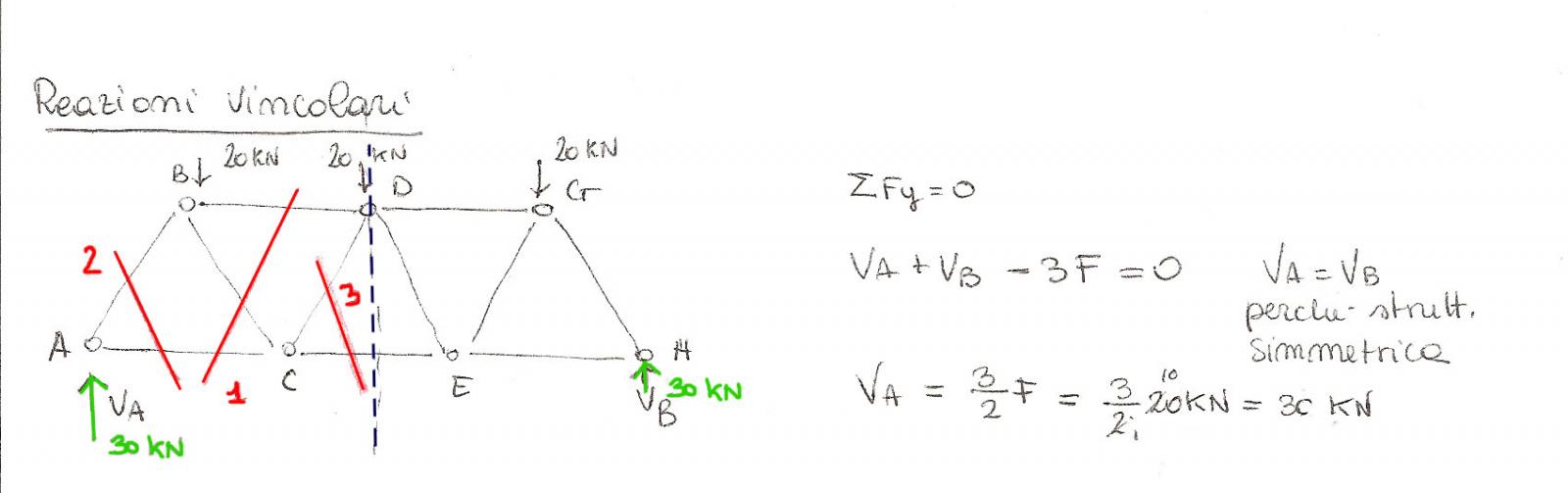
Come illustrato in figura applicando le equazioni di equilibrio otteniamo lo stesso risultato a verifica che le supposizioni precedenti erano corrette.

1.      Azioni di contatto

Per calcolare gli sforzi ai quali le aste sono soggette applichiamo il metodo delle sezioni di Ritter.

Questo metodo opera attraverso dei “tagli” sulla struttura che devono essere operati in modo da coinvolgere una serie di aste che NON concorrono nello stesso nodo.

I tagli servono a mettere in evidenza le forze interne alla struttura.

 

Ipotizziamo i versi delle forze tutti convenzionalmente positivi (aste tutte tese) in modo che se otterremo dei risultati negativi sapremo di dover cambiare il verso ipotizzato delle forze.

 

Operiamo ad esempio il taglio 1:

La porzione di struttura che consideriamo in seguito al taglio deve essere in equilibrio quindi per calcolare i valori di N₁, N₂ ed N₃ applichiamo le equazioni di equilibrio.

 

In caso di l’equilibrio alla rotazione è opportuno scegliere come centro di rotazione di volta in volta, il nodo più “comodo”.

Ad esempio facendo centro nel nodo C otteniamo  un contributo alla rotazione di N₂ ed N₃ nullo in quanto nullo è il loro braccio rispetto al centro di rotazione scelto.

Le forze in grado di far momento sono la reazione vincolare V_A (nota), la forza esterna applicata al nodo B (nota) ed N₁ che a questo punto rimane l’unica incognita.

 

Troviamo N₁= - 40 KN , il risultato è negativo perciò contrariamente a quanto ipotizzato l’asta

BD sarà compressa e soggetta ad uno sforzo pari a 40 KN.

 

Per trovare N₃ consideriamo come centro di rotazione il nodo B così che N₂ abbia braccio nullo.

Otteniamo N₃= 30  KN perciò l’asta AC è tesa.

 

Scomponendo N₂ nelle sue componenti verticale ed orizzontale  possiamo calcolarla considerando l’equilibrio alla traslazione verticale:

Otteniamo N₂= 10√2 KN , l’asta BC è tesa.

Infatti se così non fosse non avremmo equilibrio.

 

Applichiamo il taglio 2:

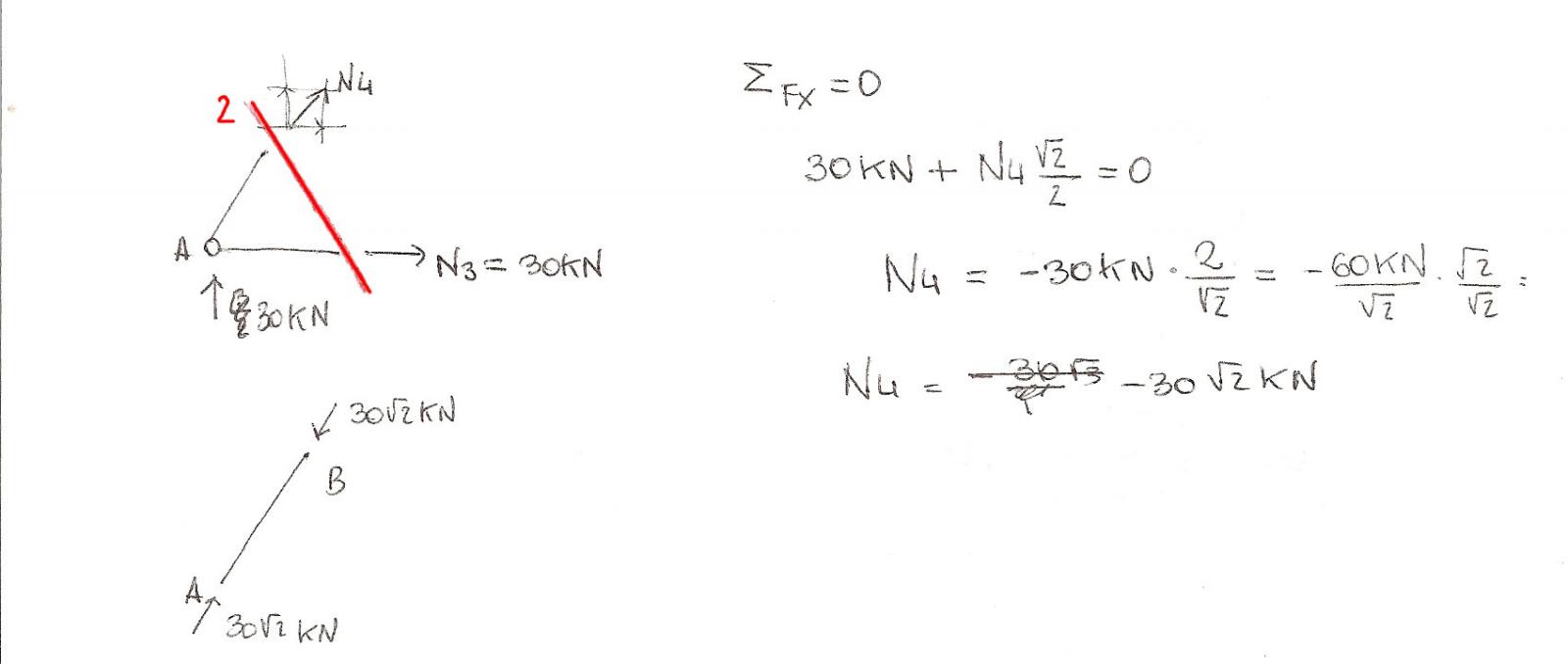
Analogamente a prima scomponiamo N₄ nelle sue componenti così che grazie all’equilibrio alla traslazione orizzontale riusciamo a calcolare N₄= -30√2 KN. L’asta AB è compressa.

 

Operiamo il taglio 3:

Considerandol’equilibrio dei momenti con centro di rotazione in D calcoliamo N₅,

N₅= 50 KN,l’asta CE è tesa;

 

Tramite l’equilibrio alla traslazione verticale troviamo N₆= -10√2 KN,  CD è compressa.

Era prevedibile che N₆ sarebbe stata di compressione, in quanto mantenendo il verso ipotizzato la componente verticale di N₆ non avrebbe equilibrato la reazione della cerniera perché avrebbero avuto lo stesso verso.

 

Grazie alla simmetricità della struttura e dei carichi possiamo estendere i risultati fin ora trovati alla restante parte della struttura, quella appunto simmetrica.

Abbiamo così calcolato le sollecitazioni che interessano la struttura.

Si noti come tutti i correnti superiori siano compressi mentre quelli inferiori tesi, comportamento tipico di una struttura reticolare appoggiata.

------------------------------------------------------------------------------------------------------------

STRUTTURA RETICOLARE ASIMMETRICA - Risoluzione con il metodo dei nodi

1.       Verifica dell’isostaticità

Da verificare                                                       v = l

 

Gradi di libertàl

l = num. aste x gradi di libertà

l = 11 x 3 = 33

I gradi di vincolo v

v = v_e + v_i

Gradi di vincolo esterni

I vincoli esterni sono una cerniera (2 gr. di vincolo) ed un carrello (1 gr. di vincolo), perciò

v_e = 2 + 1 = 3

Gradi di vincolo interni

n = 2     nodi A, H           2(2 – 1) = 2 gradi di vincolo

n = 3     nodi B, G, D      2(3 – 1) = 4            “

n = 4     nodo E               2(4 – 1) = 6           “

n = 5     nodo C               2(5 – 1) =8            “

        v_i tot = 30

perciò  v = 3 + 30 = 33 = l -> La struttura è isostatica.

 

Verifica  con metodo alternativo

v_e + aste = 2 x num. nodi

3 + 11 = 2 x (7)

14 = 14 -> isostaticità verificata

 

2.       Reazioni vincolari

Non abbiamo informazioni in merito alla simmetricità in quanto essa non è presente nella struttura, ma possiamo comunque fare delle supposizioni:

-          a differenza del caso precedente, la reazione vincolare orizzontale della cerniera in B non sarà nulla in quanto il carrello è posto in modo che la sua reazione sia anch’essa orizzontale.

Non essendoci altre componenti orizzontali O_B ed O_G saranno uguali ed opposte.

-          L’unica forza verticale in grado di opporsi al carico è la reazione verticale della cerniera che quindi sarà presumibilmente pari a 2F con verso opposto a quello dell forze concentrate F.

Con F = 10 avremo V_B= 2F= 20 KN

Applicando le equazioni di equilibrio i valori delle reazioni vincolari e notiamo che le supposizioni precedenti erano corrette.

 

1.       Azioni di contatto

Per calcolare gli sforzi ai quali le aste sono soggette applichiamo il metodo dei nodi.

Se con il metodo delle sezioni di Ritter sfruttavamo l’equilibrio tra le sezioni della struttura e le azioni di contatto, adesso considereremo l’equilibrio ai nodi sfruttando il principio per cui ogni parte della struttura (perciò anche i nodi)  deve essere in equilibrio.

 

Analizziamo quindi l’equilibrio nodo per nodo e ricaviamo i valori dello sforzo normale che interessa le aste.

Abbiamo così calcolato le sollecitazioni che interessano la struttura per cui le aste

AB , AC, CD, GE risultano scariche;

CE è l’unica asta tesa;

Tutte le aste rimanenti sono compresse.

 

Applicando alle forze dei valori numerici abbiamo potuto svolgere un’analisi della struttura anche in SAP:

Analisi dalla quale possiamo riscontrare gli stessi risultati in termini di aste tese, scariche e compresse calcolati manualmente.

 

SAP ci permette anche di vedere la deformata della struttura:

-----------------------------------------------------------------------------------------------------------

DIMENSIONAMENTO TRAVE

 

La trave che andiamo a progettare non è una semplice trave doppiamente appoggiata ma presenta anche uno sbalzo. Il valore del momento massimo non sarà quindi pari a ql²/8 (M. max in una trave doppiamente appoggiata) ma avrà un valore differente che bisogna calcolare.

Il momento massimo sarà quello a l/3 della trave con valore M_max = ql²/18

 

ANALISI DEI CARICHI E DIMENSIONAMENTO DELLA TRAVE 

Dobbiamo calcolare:

·         Carico strutturale: dipende dalla tecnologia della struttura

·         Carico accidentale: legato alla funzione.

o   Per civile abitazione (applicabile anche ad alberghi) 2KN/ mq

·         Carico permanente: dipende dagli strati che costituiscono il solaio, perciò legati alla tecnologia ma anche da elementi quali tramezzi, impianti ed intonaci applicabili alle tre tecnologie analizzate.

Considero:

o   Tramezzi 1 KN/ mq

o   Impianti 0.5 KN/mq

o   Intonaco 0.3 KN/mq

LEGNO

Carico Strutturale qs

Trave, Travetti, Tavolato =  1 KN/mq 

Ipotesi di carico del solaio ligneo per luci di dimensioni standard, supposto per il calcolo della sezione della trave.

 

Sovraccarichi permanenti qp

Pavimentazione in pietra compatta - Dati dal catalogo della ditta CITYTILE’S, prodotto COMPACT 

Spessore:      22 mm -> 0.022 m Peso al mq:  51 Kg/mq -> 0.51 KN/mq Peso al mc:   23.18 KN/mc

Massetto in malta di calce e cemento - Dati da circolare Ministeriale del 04/07/96 n.156

Spessore: 0.05 m

Peso al mq: 0.95 KN/mq

Peso al mc:        19 KN/mc

	Peso specifico (KN/mc)	Spessore (m)	Peso al mq (KN/mq)
Massetto	19	0.05	0,95
Pavimentazione	23,18	0.022	0.51

 

	Tramezzi	Impianti	Pavimentazione	Massetto	Totale
Sovraccarichi permanenti qp	1 KN/mq	0,5 KN/mq	0,51 KN/mq	0,95 KN/mq	2,96 KN/mq

 

Totale Carichi qs + qp + qa       1 KN/mq + 2,96 KN/mq + 2 KN/mq  =  5,96 KN/mq 

Carico a metro lineare q             5,96 KN/mq x interasse 4 m =  23, 84 KN/m

Calcolo del Momento massimo agente

Per una trave su due appoggi con sbalzo considero M = q x l²/18

nel caso specifico (23,84 KN/m x 8 m) / 18 =  84,8 KN x m

Ipotesi sezione della trave

Faccio riferimento ai dati reali forniti dalla ditta TECSOL produttrice di strutture in legno:

Trave in legno lamellare EUROLAM

Spessore lamelle:  40 mm

Legno: Abete Rosso

Peso specifico: 500 Kg/mc

Considerando la classe di resistenza GIL24h, inserisco fm = 24 (resistenza a trazione durante la flessione).

Il valore della tensione di progetto f_D sarà dato da

f_D= fm x K_mod/γm

Dove ym è il coefficiente di sicurezza per il legno sancito dalla normativa vigente mentre Kmod è un coefficiente moltiplicativo assegnato in funzione alla durata del carico, tiene conto che con il tempo la struttura peggiora le sue prestazioni.

Imposto una sezione di base 20 ed ottengo dal file Excel l’altezza minima indicata per la sezione, 37,82 cm.

In accordo alle dimensioni standard prodotte dall’azienda scelgo una trave di sezione 20 x 44 cm.

Calcolo dei carichi effettivi degli elementi strutturali

Trave

Area della sezione:  0,20 x 0,44 = 0,088 mq

Volume per 1 m di trave: 0,088 mq x 1 m = 0,088 mc

Peso di 1 m di trave: 0,088 mc x 500 Kg/mc =  44 kg /m à 0,44 KN/m

Porzione di trave in 1 mq : 1/interasse = 1/ 2m = 0,5 m

Peso al mq:1/ 2m x 0,44 KN/m = 0,22 KN/mq

Travetti

Interasse: 0,5 m

Luce: 4 m

Carico a metro lineare q:  5,96 KN/mq x interasse 0,5 m =  2, 98 KN/m

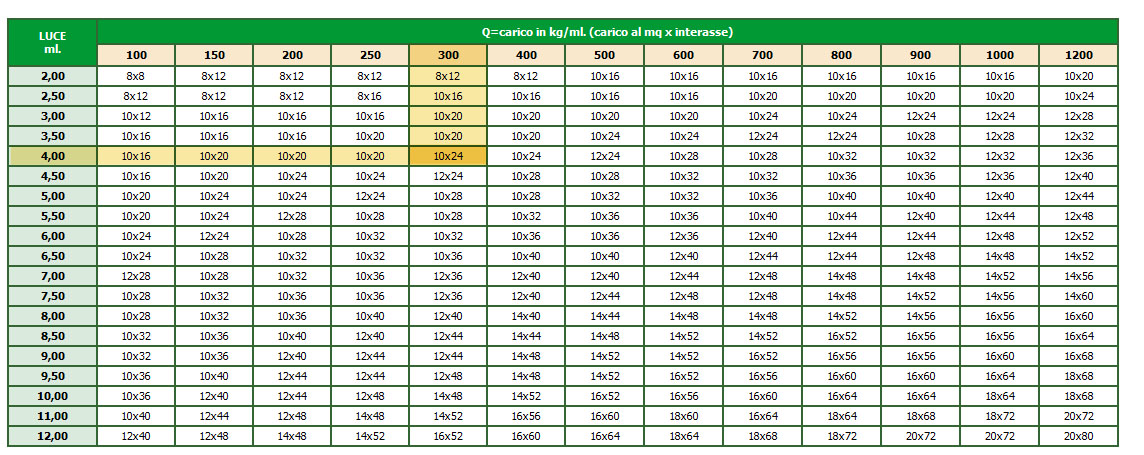
Sezione da tabelle TECSOL :  10 x 24 cm

Volume del travetto:  (0,10 x 0,24) mq  x  4 m =  0, 096 mc

Peso specifico:  0,096 mc x 500 Kg/mc = 48 Kg à 0,48 KN

Travetti in un 1 mq:  1/interasse = 1/ 1 m

Peso al mq:1/ 1m x 0,32 KN/m = 0,48 KN/mq

Tavolato

Spessore: 0,03 m

Peso specifico:  500 Kg/mc

Peso al mq: 0,03 m x 500 Kg/mc = 25 Kg/mq -> 0,25 KN/mq

 

Peso totale effettivo della struttura qs

(0,22 +  0,48 +  0,25) KN/ mq  =  0, 95 KN/ mq

Verifica della trave

Inserisco il qs effettivo  nel foglio di calcolo, l’altezza della trave ,calcolato il carico effettivo della struttura, è di 37,66 inferiore rispetto a quello calcolato in precedenza perciò la sezione di 20 x 44 rimane valida.

Verifica dei travetti

Per la verifica del travetto supposto in precedenza considero il qs effettivo a meno del carico della trave

(0,22 +  0,48 +  0,25) KN/ mq  =  0, 73 KN/ mq

ed un momento M = q x l²/8, in quanto esso si comporta come una trave doppiamente appoggiata.

Dalla tabella di calcolo ottengo un altezza del travetto inferiore ai 24 cm ipotizzati in precedenza, la sezione 10 x 24 risulta verificata.

ACCIAIO

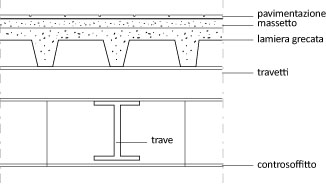
Carico Strutturale qs

Soletta in cls

Lamiera grecata

Travetti    

2 KN/mq       Ipotesi di carico del solaio in acciaio per luci di dimensioni standard, supposto per il calcolo della sezione della trave.

                       

Suppongo di usare lo stesso tipo di pavimentazione e massetto considerati nel dimensionamento della struttura in legno,  considero stavolta anche un controsoffitto

Controsoffitto

Spessore: 0,015 m

Peso al mq: 0,3 KN/mq

Peso al mc: 20 KN/mc

 

Sovraccarichi permanenti qp

Tramezzi	Impianti	Pavimentazione	Massetto	Controsoffitto	Totale
1 KN/mq	0,5 KN/mq	0,51 KN/mq	0,95 KN/mq	0,3 KN/mq	3,26 KN/mq

Totale Carichi qs + qp + qa       2KN/mq + 3,26 KN/mq + 2 KN/mq=  7,26 KN/mq

Carico a metro lineare q = (qs+qp+qa) x i = 7,26 KN/mq x interasse 4 m =  29,04 KN/m

Calcolo del Momento massimo agente

  per una trave doppiamente appoggiata con sbalzo M = ql²/18

  nel caso specifico (27,04 KN/m x 8 m) / 18 =  103,25 KN x m                     

Tensione di progetto fD

f_D =fy,k/1,15= 235 (N/mmq) /1,15 = 204,35 N/mmq

Modulo di resistenza W_x = M/ fD

W_x = (103,25 KN x m / 204,35 N/mmq) x 1000 = 505,28 cm³

Trovato W_x, modulo di resistenza a flessione della  trave . Consulto i valori tabellati per profilati metallici IPE alla ricerca di un W_x, che approssimi per eccesso quello appena calcolato.

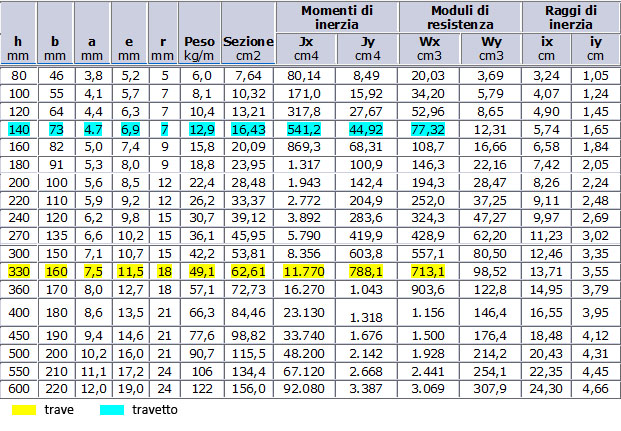
Nonostante il profilato 300 abbia un W_x maggiore di quello calcolato in precedenza scelgo un profilato IPE 330 con W_x = 713,1 cm³, per aver un margine di sicurezza superiore.

Calcolo dei carichi effettivi degli elementi strutturali

Trave 

Porzione di trave in un 1 mq:  1/interasse = 1/ 4m = 0,25 m

Peso della trave (da tabella):  49,1 Kg/m -> 0,49 KN/m

Peso al mq:1/ 4m x 0,49 KN/m = 0,12 KN/mq

Travetti

Interasse: 1 m

Luce: 4 m

Carico a metro lineare q = (qs+qp+qa) x i

7,89 KN/mq x 1 m =  7,89 KN/m

Modulo di resistenza W_x = M/ fD

W_x = (7,26 KN x m / 204,35 N/mmq) x 1000 = 71,06 cm³

Come nel caso del legno per i travetti ho considerato M = ql²/8.

Dai valori nella tabella sopra, scelgo per i travetti il profilato IPE 140   con W_x = 77,32 cm³

e peso = 0,13 KN/m

Peso specifico travetti al mq              1/ 1m x 0,13 KN/m = 0,13 KN/mq

Soletta con lamiera grecata e getto di completamento in cls

Consideriamo la lamiera A75/p570

Peso totale della soletta al mq (da valori tabellati*)         2,50 KN/mq

*“Solai con lamiera grecata” estratto da Luca Strata,  Prontuario dell'Ingegnere

Peso totale effettivo della struttura qs

(0,12 + 0,13 + 2,50) KN/mq = 2,75 KN/mq

Verifica della trave

 

Ottengo un W_x = 557,48 cm³ , inferiore a quello del profilato IPE 330 ipotizzato per la trave,  che risulta perciò verificato.

Verifica dei travetti

Per la verifica del travetto non considero il peso proprio della trave

(0,12 + 0,13 + 2,50) KN/mq = 2,63 KN/mq

Dalla tabella di calcolo ottengo un W_x = 77, 22 cm³ valore appena inferiore a quello del profilato IPE 140 scelto. In questo caso quindi sarebbe stato più opportuno scegliere il profilato IPE 160 con W_x = 108,7 cm³.

Nell’ipotesi di adottare il profilato IPE 160 per i travetti avremmo un incremento del peso dei travetti stessi.

Avremmo quindi:

Peso dei travetti al mq: 1/ 1m x 0,16 KN/m = 0,16 KN/mq

Peso totale effettivo della struttura qs:  (0,12 + 0,16 + 2,50) KN/mq = 2,78 KN/mq

Di conseguenza per la sezione un W_x = 559, 57 cm³ < W_x IPE 330

La trave con profilato IPE 330 resisterebbe quindi anche ad un maggior peso da parte dei travetti.

 

CEMENTO ARMATO

Carico Strutturale qs

Soletta collaborante

Pignatte

Travetti

Trave

3  KN/mq       Ipotesi di carico del solaio in acciaio per luci di dimensioni standard,  supposto per il calcolo   della  sezione della trave.                          

Sovraccarichi permanenti qp

Tramezzi	Impianti	Pavimentazione	Massetto	Intonaco	Totale
1 KN/mq	0,5 KN/mq	0,51 KN/mq	0,95 KN/mq	0,3 KN/mq	3,26 KN/mq

Totale Carichi qs + qp + qa       3KN/mq + 3,26 KN/mq + 2 KN/mq=  8,26 KN/mq

Carico a metro lineare q = (qs+qp+qa) x i = 8,26 KN/mq x interasse 4 m =  33, 04 KN/m

Calcolo del Momento massimo agente

  per una trave su due appoggi con sbalzo M = q x l^2/18

  nel caso specifico (33,04 KN/m x 8 m) / 18 =  117,48 KN x m

 

Tensioni di progetto di acciaio e calcestruzzo

L’acciaio impiegato come armatura nel cls appartiene alle classi B450A o B450C. Per entrambe il valore massimo della tensione è fy = 450 Mpa ed il valore di rottura è fissato a 540 Mpa ma i due tipi si differenziano in quanto il secondo presenta un allungamento a rottura maggiore ( ε =7 % per B450C mentre  ε = 3 % per B450A) . In zona sismica deve essere obbligatoriamente impiegato l’acciaio B450C in quanto duttile e di conseguenza più affidabile.

Per il progetto della trave scelgo un acciaio B450C (fy = 450 Mpa e limite d rottura a 540 Mpa).

Per calcolare il valore di progetto della tensione per l’acciaio di armatura dovrò dividere il valore della tensione massima fy per un coefficiente di sicurezza y_m = 1,15 ( differente dal  y_m = 1,05 impiegato per l’acciaio da carpenteria).

Ottengo quindi fd_f = fy/ y_m = (450 N/mm²) / 1,15 = 391,30 N/mm²

                                              

Per il calcestruzzo scelgo un calcestruzzo ordinariodi classe C40/50 con fck = 40 N/mm²

Il valore di progetto della tensione per il calcestruzzo sarà pari al valore di resistenza cilinfìdrica fck  diviso il coefficiente di sicurezza y_m = 1,75.

Ottengo quindi fd_c = fck/ y_m = (40 N/mm²) / 1,15 = 22,86 N/mm²

Dimensionamento della sezione

L’altezza della sezione H è la somma dell’altezza utile (hu),  con la distanza (δ)  tra il centro dell’armatura ed il lembo inferiore della sezione. L’altezza utile hu indica la distanza tra il lembo compresso della sezione in c.a. e l'armatura tesa. Consideriamo una sezione di base b = 25 cm con δ = 5 cm e calcoliamo l’altezza  utile hu. hu = r √(M/ fD_c x b) = 32,29 cm con r = 2,25 Troviamo l’altezza totale della sezione H = hu + δ = 32,29 cm + 5 cm = 37, 29 cm

Considero una sezione di 25 cm x 45 cm.

Una volta dimensionata la sezione della trave possiamo calcolarne il carico strutturale effettivo sostituendolo al qs standard di 3 KN considerato in principio.

Calcolo dei carichi effettivi degli elementi strutturali

Trave

Area della sezione:  (0,25 x 0,45) m = 0,11 mq

Peso: 2,81 KN/m

Porzione di trave in un 1 mq:  1/interasse = 1/ 4m

Peso specifico in 1 mq: 1/ 4m x 0,11 KN/m = 0,028 KN/mq

Pignatte

Dati da Sarda Laterizi spa.

Area pignatta: (0,16 x 0,38) m = 0,06 mq

In un mq di solaio ci sono 8 pignatte.

Peso al mq: 8 x (8,3 Kg) = 66,4 Kg = 0,66  KN/mq

 

Travetti

Area del travetto: 0,10 x 0,16 = 0,016 mq

Volume del travetto:  (0,10 x 0,16) mq  x 1m =  0, 016 mc

Peso specifico del cls 25 KN/mc

Peso specifico dei travetti in 1m : 0,016 mc x 25 KN/mc  = 0,4  KN/m

Travetti in un 1 mq:  1/0,48 m

Peso specifico in 1 mq:  1/ 0,48 m x 0,4 KN/m = 0,83 KN/mq

 

Soletta

Spessore della soletta 0,04 m

Peso al mq  0,04 m x 25 KN/mc = 1 KN/mq

 

Peso totale effettivo della struttura qs

(0,028+  0,66 +  0,4 + 1) KN/ mq  =  2 KN/ mq

Inserisco il qs trovato nel foglio di calcolo: l’altezza della trave, calcolato il carico effettivo della struttura, è di 35,27 cm perciò la sezione di 25 x 45 cm ipotizzata in precedentemente rimane valida.

--------------------------------------------------------------------------------------------------------------------------------------------

PROGETTO DELLE ASTE DI UNA TRAVATURA RETICOLARE SPAZIALE IN ACCIAIO

Disegniamo in Autocad la travatura reticolare tridimensionale per poi esportarla in SAP ed effettuarne l’analisi.

Disegno della struttura – Autocad

Il layer 0 di Autocad non viene riconosciuto da SAP perciò innanzitutto creiamo un nuovo layer su cui disegneremo la struttura.

La strutture reticolare che andremo ad analizzare ha matrice cubica,  dobbiamo immaginarla come una composizione di 6 x 4  cubi di cui le aste costituiscono gli spigoli e le diagonali di ciascuna faccia.

1. Partiamo dal disegno in piano del singolo modulo a “C” che ci permetterà di disegnare l’intera struttura. È importante creare tale matrice in modo che copiandola non ci siano aste sovrapposte che ne impedirebbero in seguito l’analisi. La struttura ha un modulo quadrato di lato 2 di conseguenza la lunghezza della aste oblique sarà 2√2.

2.  Replichiamo la matrice con il comando copia in serie (array) e chiudiamo l’ultima campata in modo da ottenere un prospetto di 4 moduli.

3.  Passiamo alla visualizzazione 3D e ribaltiamo il modulo lineare ottenuto sul piano z-x

4.  Ricopiamo il modulo a C lungo l’asse y ed aggiungiamo le diagonali alla base inferiore e superiore della seconda fila di “cubi”,  con copia in serie completiamo la seconda campata.

5.  Ottenuta questa nuova matrice la copiamo ancora una volta con Array, facendone 6 copie. Il comando Array crea la copia lungo l’asse x perciò sarà necessario prima della copia cambiare l’ucs.

6.  Chiudiamo l’ultima campata, selezioniamo l’intera struttura e tramite il comando esplodi esplodiamo eventuali blocchi o polilinee che impedirebbero la lettura in SAP

7.   Salviamo il file in .dxf nella versione di autocad 2000 per evitare problemi di incompatibilità.

Analisi della struttura – SAP 2000

Con Autocad abbiamo disegnato il modello 3D della struttura, in SAP aggiungeremo le informazioni relative a materiale, carichi e vincoli.

1. Importiamo il file .dxf creato in Autocad:  come Import Information  selezionare l’unità di misura  e gli assi di riferimento in uso; nella finestra DXF Import selezionare dal menù a tendina alla voce frames il layer su cui abbiamo disegnato la struttura.
2. Assegniamo i vincoli esterni alla struttura: 4 cerniere nei quattro angoli dove ipotizziamo essere degli appoggi;

3.  Definiamo il materiale –acciaio- e la sezione degli elementi –tubolare (pipe);

4.  Assegniamo i vincoli interni: in una struttura reticolare le aste sono connesse tra loro da cerniere interne, perciò selezioniamo tutte le aste e rilasciamo i momenti alle estremità (nella direzione 22 e 33 perché stiamo lavorando con un modello tridimensionale);

5.   Definiamo e successivamente assegniamo i carichi sui nodi. In questo caso avremo per ciascun nodo superiore una forza concentrata gravitazionale di 40 KN.

 

6.  Prima di lanciare l’analisi spuntiamo l’opzione che ci permette di visualizzare una numerazione delle  aste in modo da renderle riconoscibili nell’analisi successiva;

7.  Lanciamo l’analisi.

8.  Apriamo le tabelle relative all’analisi:

la tabella ci mostra i risultati per ogni singola asta. Per ciascuna sono presenti 3 valori, SAP mostra infatti il valore delle sollecitazioni alle due estremità e nel punto medio ( ad esempio per un’asta di 2 metri avremo in tabella i valori a 0 estremo iniziale, 1 mezzeria, 2 estremo finale)

Come previsto i contributi di taglio V e momento M sono nulli, mentre compaiono i valori dello sforzo normale N.

Per il progetto delle aste dobbiamo individuare i valori massimo di N per le aste tese e per quelle compresse, differenziando tra queste le aste rette (lunghezza 2 m) e le aste diagonali (lunghezza 2√2 m).

Per una più rapida (e comoda) lettura della tabella la esportiamo in Excel in modo da poter ordinare i valori in ordine crescente.

La lunghezza delle aste si riconosce dalla seconda colonna (STATION) in cui, come già detto sopra, vengono mostrati i valori alle estremità ed in mezzeria. Avremo che le aste con station 0-1-2 saranno quelle rette di 2 m, mentre le aste 0-1,41-2,83 saranno quelle diagonali.

Ricordando la convenzione per cui uno sforzo normale di trazione ha segno positivo mentre uno di compressione ha segno negativo, individuiamo i valori massimo necessari al progetto delle aste.

Trovato il valore massimo di N possiamo proseguire con il progetto e la verifica della sezione.

Progetto e verifica delle aste

La struttura reticolare in acciaio è formata da una serie di aste che sono soggette a solo sforzo normale, come risulta anche dall’analisi in SAP.

Tenendo conto che la struttura  è  in acciaio dobbiamo ricordare che,  nonostante per questo materiale il valore di resistenza a  trazione sia uguale a quello a compressione,  gli elementi tesi e quelli compressi non si comportano allo stesso modo.

Le aste della struttura sono elementi snelli, ovvero elementi in cui risulta elevato il rapporto h/l,  tra l’altezza dell’elemento h e la sua larghezza l. In quanto snelle le aste soggette a compressione possono essere interessate dal fenomeno di instabilità euleriana.

L’instabilità euleriana è il fenomeno fisico che tiene conto che un elemento eccessivamente snello soggetto ad un carico di punta può sbandare.

Per la verifica dell’asta bisogna quindi calcolare il valore del carico critico euleriano P_crit, quindi considerando P il valore massimo dello sforzo normale,  

se  P ≥ P_crit l’asta risulterà instabile;

se  P ≤ P_crit l’asta risulterà stabile.

Il carico critico euleriano è

P_crit = π² x E x J_min / l₀²

Con E = modulo elastico a compressione  del  materiale considerato

J_min = momento d’inerzia minore della sezione

l₀ = lunghezza libera di inflessione

Tiene conto delle caratteristiche del materiale (E) e della sezione (J_min) ma anche della qualità dei  vincoli che agiscono sull’elemento in analisi.

L’asta di una travatura reticolare ha come vincolo le due cerniere interne poste alle sue estremità, queste fanno si che il momento agli estremi dell’asta sia nullo, perciò l’asta si comporta come nel caso

in cui l₀ = l

Essendo la lunghezza libera di inflessione strettamente legata alla lunghezza l dell’asta, le aste di diversa lunghezza avranno quindi un diverso P_crit , andranno perciò progettate e verificate separatamente.

Come abbiamo già visto le aste della nostra struttura reticolare sono di due lunghezze, la minore relativa alle aste verticali ed orizzontali, la maggiore relativa alle aste oblique.

Per questo nelle tabelle generate da SAP dovremmo individuare:

-  N massimo di compressione per le aste minori;

-  N massimo di compressione per le aste maggiori;

-  N massimo per le aste tese.

Per quanto riguarda le aste tese la differenza di lunghezza tra le aste è indifferente, in quanto la lunghezza della trave non ne influenza il progetto. Per queste aste dovremmo effettuare la verifica a rigidezza del materiale.

La sezione delle aste  viene scelta in base allo sforzo N massimo che agisce su essa perciò una volta calcolata l’area della sezione A = N/fD approssimeremo questo valore per eccesso scegliendo tra i profili tabellati.  Eseguiremo quindi la verifica all’instabilità per i puntoni soggetti a N maggiore e la verifica a rigidezza per il tirante più sollecitato.

Per la verifica a rigidezza (tiranti), affinché l’asta sia verificata la tensione σ dovrà essere minore del valore della tensione di progetto fD

σ = N/A ≤ fD

N = sforzo normale massimo calcolato dall’analisi

A = sezione scelta

fD = fyk/γ = tensione di progetto, calcolata come il rapporto tra fyk – tensione di snervamento per la classe di resistenza scelta – e  γ, coefficiente di sicurezza per l’acciaio da carpenteria (pari a 1,05).

Asta tesa

L’asta tesa maggiormente sollecitata (asta 128) è soggetta ad uno sforzo normale di 258,934 KN.

Consideriamo le classi di resistenza per l’acciaio da carpenteria Fe 360 S235, Fe 430 S275, Fe 510 S355 e definiamo la sezione del tirante per ciascuna delle tre classi.

La sezione A = N/ fD perciò calcoliamo fD= fyk/y con y =1,05 ed fyk che varia a seconda della classe di resistenza:

Nella colonna A minima è riportato il valore dell’area minima della sezione, mentre in A l’area delle sezioni desunta dai valori tabellati per tubolari che approssimano per eccesso il valore dell’area minima calcolato.

Calcoliamo il valore della tensione σ = N/A inserendo come A i valori delle sezioni scelte. Per tutte e tre le classi di resistenza i tiranti risultano come previsto verificati in quanto σ  ≤ fD.

Asta compressa lineare (2 m)

Progetto

L’asta compressa maggiormente sollecitata,  tra quelle più corte (asta 103) è soggetta ad uno sforzo normale di 296,771 KN ( in tabella il valore è negativo in quanto di compressione).

Come per il tirante, consideriamo le classi di resistenza dell’acciaio Fe 360 S235, Fe 430 S275, Fe 510 S355 e quindi considerando il valore fD calcolato in precedenza troveremo l’area minima della sezione come A = N/ fD

 in A sono riportate le aree per le sezioni scelte dai valori tabellati per tubi in acciaio a sezione circolare

Verifica all’instabilità

Dobbiamo calcolare il carico critico euleriano P_crit = π² x E x J_min / l₀²

Conosciamo la lunghezza libera di inflessione in quanto la nostra situazione ricade nel caso in cui l₀ = l per cui avremo l₀ = 2 m = 2000 mm;

Il momento d’inerzia minore della sezione J_min si desume dai valori tabellati;

Il  modulo elastico E  dipende dalla classe di resistenza del materiale scelta.

Continuiamo con un’analisi in parallelo per  tre classi di resistenza, per cui:

Per Fe 360 S235, E = 190000N/mmq;

Per Fe 430 S275, E = 200000N/mmq;

Per Fe 510 S355 E,  = 210000N/mmq

Per il calcolo del P critico impiego una tabella excel:

Avendo scelto di convertire le lunghezze nell’ordine dei mm ottengo Pcrit in N

[(N/mmq x mm4) / mmq ] = [N]

con un ulteriore conversione riporto il valore in KN in modo da poterlo confrontare con il valore di P.

Affinchè le aste siano verificate dobbiamo avere che P ≤ P_crit

Essendo P = 296,771 KN le aste progettate sono tutte e 3 stabili.

 

Asta compressa diagonale (2√2 m)

Progetto

L’asta compressa maggiormente sollecitata,  tra quelle più lunghe (asta 255) è soggetta ad uno sforzo normale di 307,254 KN ( in tabella il valore è negativo in quanto di compressione).

La diversa lunghezza dell’asta non influenza il calcolo della sezione, perciò rimangono validi i valori calcolati sopra per l’asta compressa più corta.

Verifica all’instabilità

La lunghezza maggiore implica invece una variazione del carico critico euleriano, dove la lunghezza gioca una ruolo principale, perciò con l = 2,82 m avremo l₀= 2820 mm e di conseguenza:

 

Affinchè le aste siano verificate dobbiamo avere che P ≤ P_crit

Essendo P = 307,254 KN, l’asta progettata con classe di resistenza maggiore risulta instabile in quanto

307,254 KN >  228,86 KN.

Dall’analisi in parallelo delle stesse asse progettate con diversa classe di resistenza si nota quanto la dimensione della sezione influisca in termini di instabilità: dalla fase di progetto è evidente che impiegando una classe di resistenza maggiore si ottiene un’asta di sezione minore, di conseguenza si avrà un J minore e questa stessa asta sarà soggetta ad un carico critico euleriano molto inferiore rispetto alle altre. L’asta  risulterà, tra quelle analizzate, potenzialmente la meno stabile.

Infatti se per l’asta di lunghezza 2 m anche quella con classe di resistenza massima risultava verificata, aumentando la lunghezza a 2,82 m vediamo che questa stessa asta risulta instabile.

Per la classe di resistenza Fe 510 S355 sarà opportuno impiegare una sezione maggiore.

Neanche la sezione subito successiva risulta verificata, perciò affinchè l’asta risulti stabile dovremmo adottare la medesima sezione già scelta per la classe di resistenza Fe 430 S275, ovviamente seppure la sezione è la stessa il valore di P crit cambia in quanto per le due classi di resistenza varia E.

Otteniamo con questa nuova sezione P crit = 499,9 perciò P < Pcrit, l’asta è verificata.

 

------------------------------------------------------------------------------------------------------------------------------------------------

RIPARTIZIONE DELLE FORZE SISMICHE

Il telaio oggetto dell’esercitazione  presenta 8 controventi, rispettivamente 4 verticali e 4 orizzontali.

Ipotizziamo una struttura in c.a. con pilastri di sezione rettangolare di (30x 40) cm.

Ix = bh³/12 = 90000 cm⁴

Iy = hb³/12 = 160000 cm⁴

 

La disposizione dei pilastri in pianta non è casuale, ma tiene  conto del carico verticale proveniente dal solaio.

Le travi che portano il solaio saranno soggette ad un inflessione maggiore rispetto alle altre, perciò i pilastri di sezione rettangolare, come quelli ipotizzati, vengono disposti in modo che il momento di Inerzia maggiore della sezione agisca nella direzione più sollecitata.

In caso di pilastri d’angolo (come il pilastro 11), in cui confluiscono cioè due travi, la direzione più sollecitata sarà quella della trave più lunga che (nell’esempio trave 12-11), in quanto tale, subirà un’inflessione maggiore rispetto alla trave più corta (11-10).

STEP 1 - calcolo delle rigidezze traslanti dei controventi dell'edificio

Tutti i controventi sono ipotizzati Shear-type, la loro rigidezza sarà perciò pari a:

Kt= 12 x E x  J_tot /h³

Con

E = modulo di Young,  per il c.a. E = 21000 N/mmq

h = altezza del telaio, scegliamo h = 3,20 m

J_tot = momento di inerzia totale, pari cioè alla somma dei momenti di inerzia dei singoli pilastri.

Bisogna infatti tenere conto che in un singolo telaio possiamo avere pilastri con diversi momenti d’inerzia. 

Come conseguenza della disposizione dei pilastri in pianta (che come abbiamo visto tiene conto dei carichi verticali), in un singolo telaio si possono avere pilastri disposti in maniera diversa, quindi data la sezione rettangolare dei pilastri, una volta che il telaio sarà soggetto alla forza sismica orizzontale, i momenti di inerzia reagenti saranno differenti.

 

Ad esempio nel telaio 2-11-10-9 l’inflessione dei pilastri 2-11 avverrà intorno all’asse parallelo al lato maggiore. Perciò il J reagente sarà quello intorno a tale asse pari a Jx= b x h3 /12 = (40 x (30)3 ) cm/12 = 90000 cm4 L’inflessione dei pilastri 10-9 avverà invece intorno all’asse parallelo al lato minore della sezione, con Jx = b x h3 /12 = (30 x (40)3 ) cm/12 = 160000 cm4

Inserendo nel foglio excel i dati relativi a ciascun telaio, ne calcoliamo la rigidezza:

khjhlhlhjlh

Step 2: tabella sinottica controventi e distanze

La tabella riporta le rigidezze di ogni singolo telaio e le relative distanze calcolate dal punto O, origine del sistema di riferimento impiegato.

Step 3: calcolo del centro di massa

Calcoliamo le coordinate X_G,Y_G del centro di massa.

Il nostri impalcato è un’area a T che possiamo agevolmente suddividere in due aree rettangolari di cui conosciamo le coordinate dei  centri di massa (X_G1,Y_G1 ; X_G2,Y_G2)

Inseriamo tali coordinate nel file excel e otteniamo la posizione del centro di massa G dell’impalcato.

Note le coordinate dei centri di massa delle aree minori,  X_G,Y_G vengono calcolate in questo modo:

X_G =( A₁ x X_G1+ A₂ x X_G2) / (A₁+ A₂)

Y_G  =( A₁ x Y_G1+ A₂ x Y_G2) / (A₁+ A₂)

Come si vede dalla tabella otteniamo           X_G = 10,5 m                 Y_G  = 10,76 m

Step 4: calcolo del centro di rigidezze e delle rigidezze globali

Sommando le rigidezze dei singoli telai riportate nella tabella allo step 2 otteniamo le rigidezze totali

K_x tot =  rigidezza totale orizzontale 

K_y tot = rigidezza totale verticale

Possiamo quindi calcolare le coordinate del centro delle rigidezze C, ovvero del centro di rotazione situato sull’asse delle rigidezze. Sotto l’azione della forza sismica, se essa non agisce lungo l’asse delle rigidezze, l’impalcato tenderà a ruotare intorno a C.

X_c = (K_y1 x d_y1 + Ky2 x d_y2+ K_y3 x d_y3 + K_y4 x d_y4 )/ (K_x tot)

Y_c = (K_x1 x d_x1 + Kx2 x d_x2+ K_y3 x d_x3 + K_y4 x d_x4 )/ (K_y tot)

I telai dovranno perciò contrastare anche la rotazione, per questo sviluppano una rigidezza torsionale.

La rigidezza torsionale totale, note le distanze dei telai (dd_xn , dd_yn) da C , può essere calcolata come

K_ϕ= Ʃ_i k_i dd_i²

Step 5: analisi dei carichi sismici

La forza sismica è una forza d’inerzia dovuta allo scuotimento del suolo.

In quanto tale essa è il prodotto di una massa per una accelerazione:

F = m x a

Dove la massa m è la massa della struttura ed  a è l’accelerazione di trascinamento proveniente dal basso (dal suolo).  a è l’accelerazione massima che acquista la struttura quando il terreno è scosso; in una struttura molto rigida la a della struttura sarà pari a quella del suolo mentre in una struttura flessibile la a sarà solo una porzione di quella del suolo.

Dalla normativa a viene considerata come una frazione dell’accelerazione gravitazionale g per cui

a = c x g con c < 1 coeff. di instabilità sismica

Possiamo quindi notare che

F = m x a = m x c x g = c x (m x g)

Dove (m x g) è proprio il peso W della struttura, perciò avremo

F = c x W

Per calcolare il peso della struttura dobbiamo considerare il peso strutturale (q_s) , i sovraccarichi permanenti  (q_p) ed i sovraccarichi accidentali (q_a).

Determiniamo il carico totale permanente G come

G = (q_s + q_p) x Area _tot dell’impalcato

Ed il carico totale accidentale Q come

Q = (q_a) x Area _tot dell’impalcato

Il peso W della struttura sarà perciò pari a

W = G + y Q

con Q diminuito di un coeff. di partecipazione y.

Trovato W, possiamo finalmente calcolare la forza sismica  F = c x W , il cui valore è riportato in tabella.

 

Step 6 e Step 7: ripartizione forza sismica lungo due direzioni ortogonali

La direzione del sisma non è prevedibile perciò simuliamo e verifichiamo la struttura in due direzioni ortogonali, come richiesto dalla normativa.

Abbiamo calcolato il valore delle rigidezze traslanti dei telai (Step 1-2) che si oppongono alla traslazione dell’impalcato, ed il valore della rigidezze torsionali (Step 4) che si oppongono alla rotazione dell’impalcato.

Come accennato sopra, l’impalcato soggetto alla forza sismica può essere oggetto non solo di una traslazione ma anche di una rotazione.

La rotazione può verificarsi se i controventi non hanno tutte le stesse rigidezze o se la forza non agisce lungo l’asse delle rigidezze.

La forza sismica si considera applicata lungo l’asse del centro di massa G, perciò se G non è allineato con il centro delle rigidezze C  (come nella maggior parte dei casi) si creerà un momento torcente M:

M = F x b

Dove b sarà il braccio della forza ovvero la differenza delle coordinate dei due punti G, come punto di applicazione della forza sismica F e C come centro di rotazione in quanto centro delle rigidezze.

Vedremo infatti che nel nostro caso si verifica una rotazione dell’impalcato se la forza sismica è applicata lungo x, mentre per  F lungo y non si ha rotazione in quanto C e G sono allineati e perciò il braccio della forza risulta nullo.

Nelle tabelle seguenti sono stati calcolati il valore del momento torcente M, della traslazione u verticale o orizzontale e della rotazione ϕ.

 

 

La traslazione u₀ si calcola come u₀ = F/ K_{0 tot}

La rotazione ϕ₀ sarà uguale a  ϕ₀ = M/ K_{ϕ tot}

Inoltre viene calcolato come la forza sismica si ripartisce nei singoli controventi.

Ognuno dei controventi orizzontali avrà una reazione pari a

R_i^O= K_i^O x (u_i+ ϕd_i^O) 

Ognuno dei controventi verticali avrà una reazione pari a

R_i^v= K_i^v x (u_i+ ϕd_i^v)