esercitazione 4_metodo delle forze

Esercitazione 4

Metodo delle forze

Soluzione di una struttura tre volte iperstatica

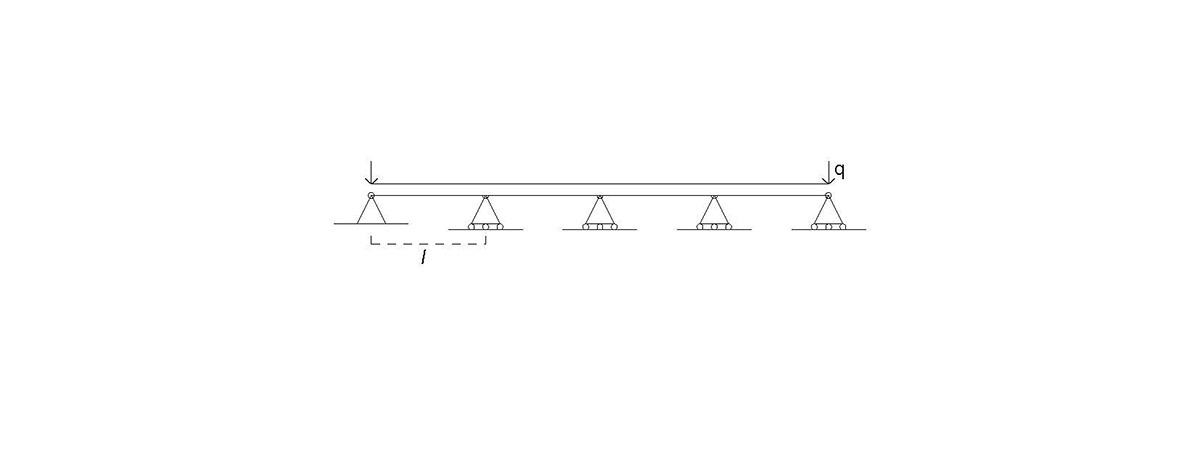
N.B.

Sono noti i valori della rotazione per la trave appoggiata a cui sono applicati:

a.       un carico uniformemente distribuito

φ₁  = ql²/24EJ

b.      un momento applicato ad un estremo

φ₁  = xl/3EJ

φ₂= xl/6EJ

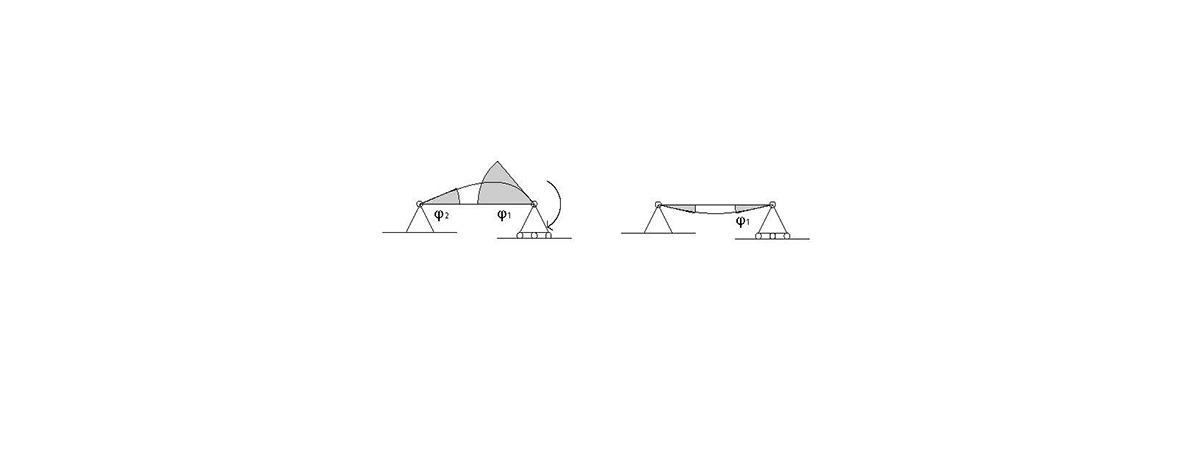
Analizzando qualitativamente I vincoli, si possono fare alcune considerazioni utili ai fini della risoluzione del sistema:

Nel punto B la rotazione delle sezioni dev’essere uguale da sinistra e da destra.

Lo stesso avviene per il punto C e il punto D.

Φ_{b sx}=  Φ_{b dx}

Φ_{c sx}=  Φ_{c dx}

Metodo delle forze

Posso concepire un sistema isostatico equivalente, dal punto di vista cinematico, a quello dato, per procedure con la risoluzione del sistema.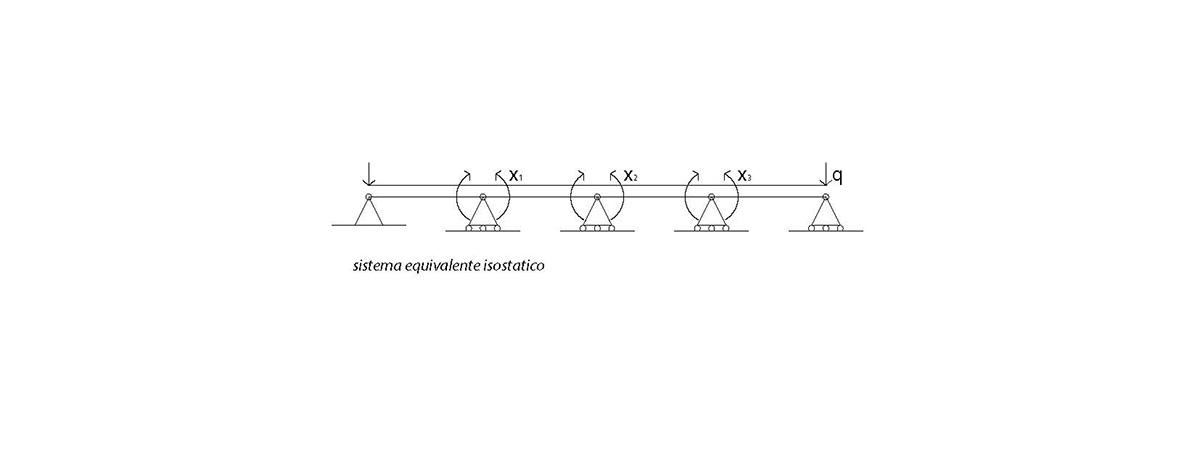

Tale sistema sostituisce all’unica trave una serie di travi appoggiate di luce l e collegate da carrelli, sui quali viene applicato un momento di valore incognito x, che deve servire a compensare il rilascio alla rotazione relativa effettuato attraverso il distacco dei tratti di trave.

N.B.

Analizzando la struttura dal punto di vista qualitativo, ci si accorge che questa ha caratteri di simmetria che consentono di ipotizzare che le reazioni vincolari siano in B e D uguali (e quindi anche i momenti applicati in quei punti del sistema equivalente), come pure in A ed E.

Riepilogando:

R_a = R_e ;

R_b = R_d ;

x₁ = x₃

(B)

Φ_{b sx}=  -(x₁l / 3EJ) + (ql³ / 24EJ)

Φ_{b dx}= (x₁l / 3EJ) – (ql³ / 24EJ) + (x₂l / 6EJ)

(C)

Φ_{c sx}=  -(x₂l / 3EJ) - ( x₁l / 6EJ) + (ql³ / 24EJ)

Φ_{c dx}= (x₂l / 3EJ) - (ql³/ 24EJ) + (x₃l / 6EJ)

Eguaglio a due a due queste equazioni (sostituendo anche x₃ con x₁), andando ad impostare un sistema di due equazioni in due incognite (x₁ e x₂).

ì-(x₁l / 3EJ) + (ql³/ 24EJ) = (x₁l / 3EJ) – (ql³/ 24EJ) + (x₂l / 6EJ)

í

î-(x₂l / 3EJ) - ( x₁l / 6EJ) + (ql³ / 24EJ) = (x₂l/3 EJ) - (ql³ / 24EJ) + (x₃l / 6EJ)

ì-2x₁l /3 = (-ql² / 4) (-3 / 2l)  => x₁ = (ql² / 8) – (x₂ / 4)

í

î(- x₂l / 3) – (l/6) [(ql²/8) – (x₂ / 4)]+ ql³ / 24 = (x₂l / 3) – (ql³ / 24) + (l/6) [(ql²/8) – (x₂ / 4)]

ì------------------

í

î- (2x₂l / 3) – (l/3) [(ql²/8) – (x₂ / 4)]+ ql³ / 12 = 0

ì------------------

í

î- (2x₂l / 3) – (ql³ / 24) + (ql³ / 12) (x₂ / 12) = 0

per cui

x₂ = ql² / 4=> x₁ = 3ql² / 28

Ora si procede grazie al principio di sovrapposizione degli effetti: infatti il sistema equivalente può essere inteso come sovrapposizione di due sistemi in cui, come forze esterne, una volta viene considerato solo il carico distribuito (schema q) ed una volta solo i momenti applicati sui carrelli, il cui valore è stato appena definito (schema x).

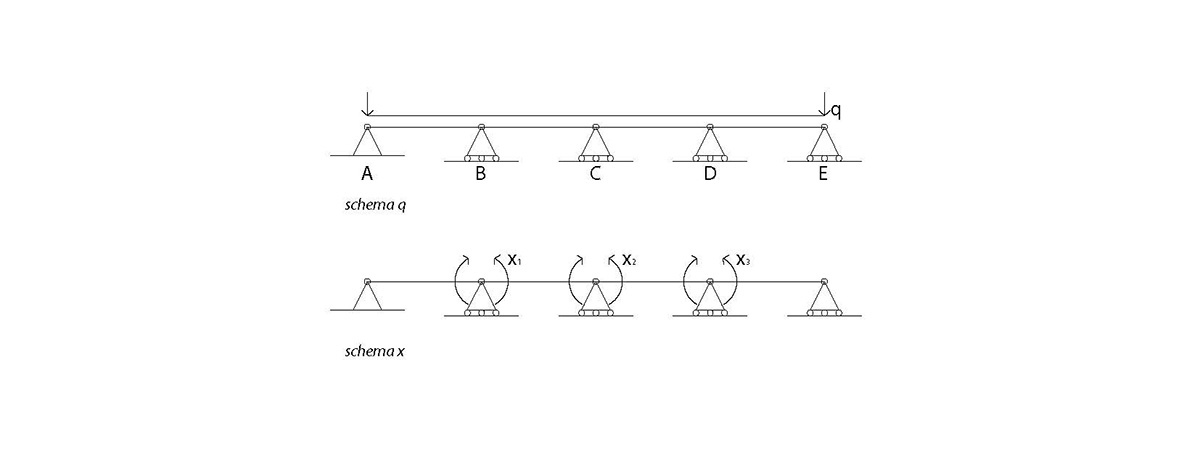
Si trovano le reazioni vincolari dei due sistemi per poi sommarle (sovrapposizione degli effetti):

Schema x:

R_{a x} = x₁/l

R_{b x} = (x₁/l) + (x₁ – x₂)/l

R_{c x} = 2 [(x₁ – x₂)/l]

Schema q:

R_{a q} = R_{e q} = ql/2

R_{b q}= R_{c q} = R_{d q} = ql

N.B.

Le reazioni sono calcolate analizzando separatamente ogni asta appoggiata-appoggiata e poi sommando I risultati ottenuti sui punti in comune delle aste adiacenti.

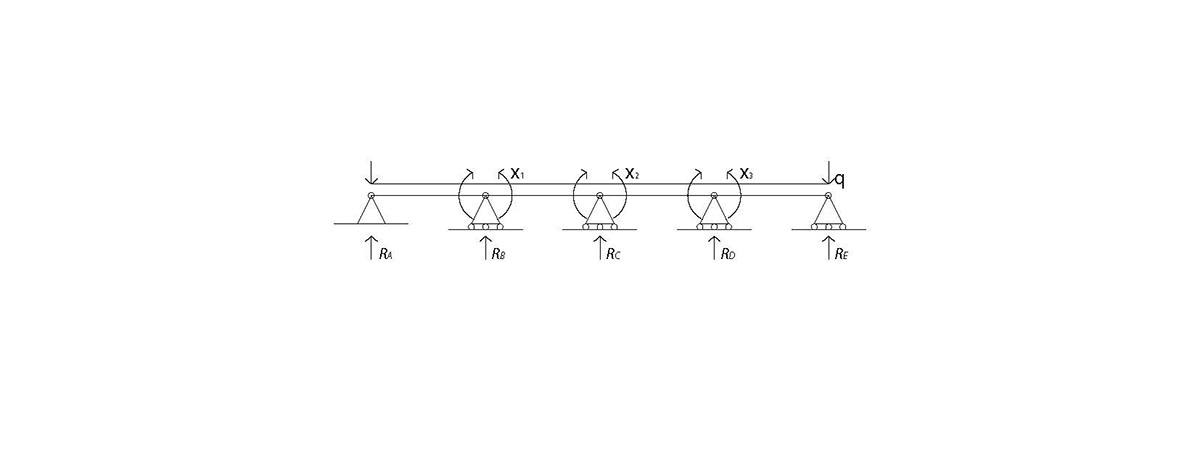
Schema equivalente completo:

(ipotizzando la reazione risultante verso l’alto)

R_a = ql/2 – (3ql²)/l = 11ql/28

R_b = ql – [(3ql²/14) – (ql²/14)]= ql + (2ql/14) = 8ql/7

R_c = -(2/l) [(3ql²/28) – (ql²/14) + ql = ql – (2ql/28) = 13ql/14

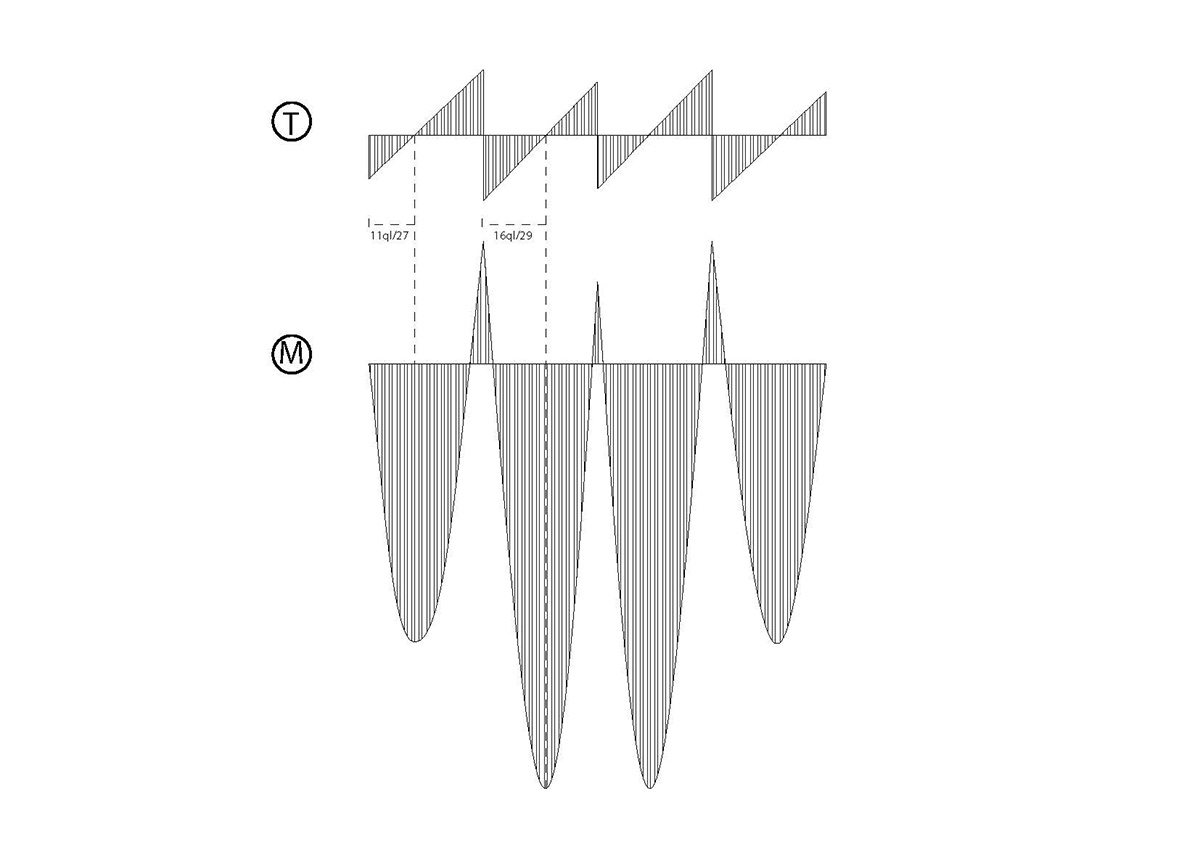
Ora si procede con l’analisi delle sollecitazioni di taglio e momento: