QUINTA ESERCITAZIONE: Metodo delle forze
RISOLUZIONE DI UNA STRUTTURA IPERSTATICA CON IL METODO DELLE FORZE
1.Struttura iperstatica ( 3 volte)
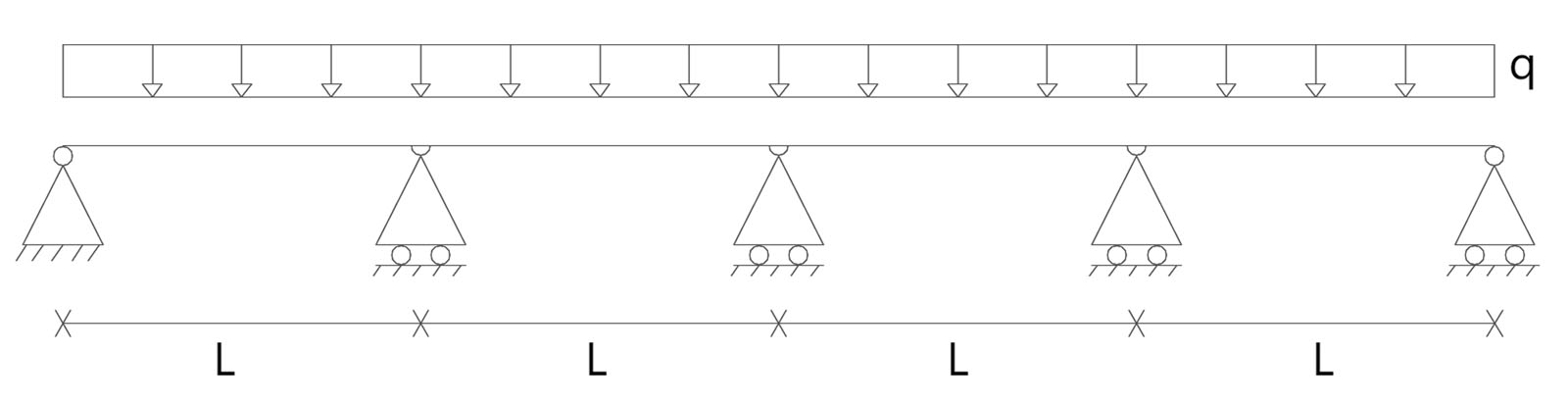
2. Struttura isostatica di riferimento e individuazione delle incognite iperstatiche
-Vincolo rimosso = rotazione relativa tra i corpi
-Incognita iperstatica = momenti X1 - X2 - X3
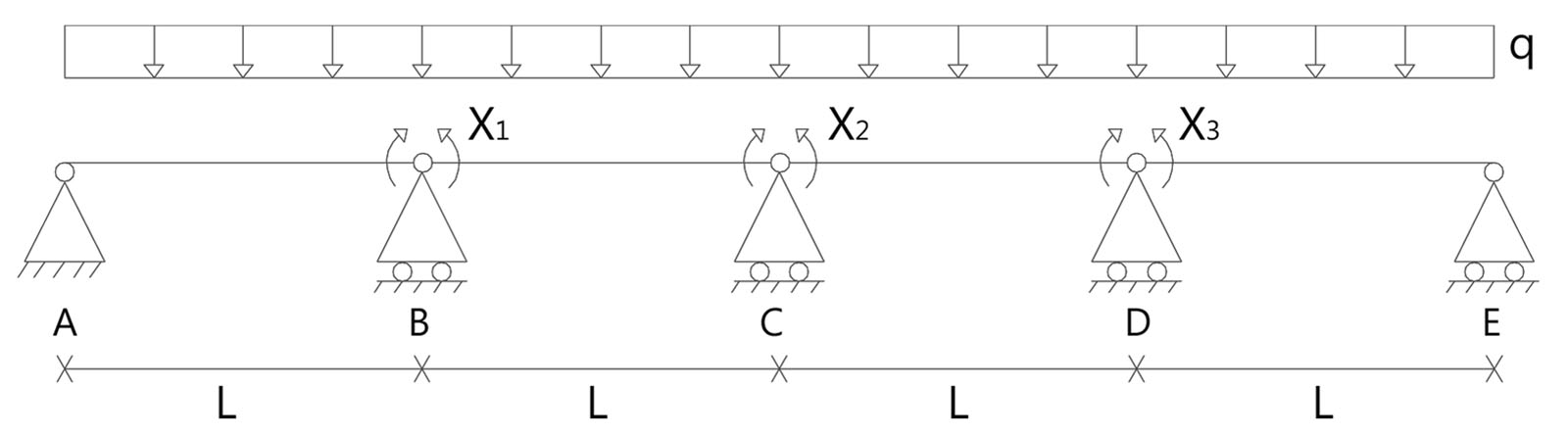
3. Scrittura delle equazioni di compatibilità cinematica che ripristinino i vincoli cinematici soppressi dalla trasformazione del vincolo cinematico in forza (reazione vincolare)
-Dagli schemi noti sappiamo che la rotazione ϕ in una trave doppiamente appoggiata con ,
rispettivamente applicato, un carico ripartito" q" ed un momento concentrato "m" vale:
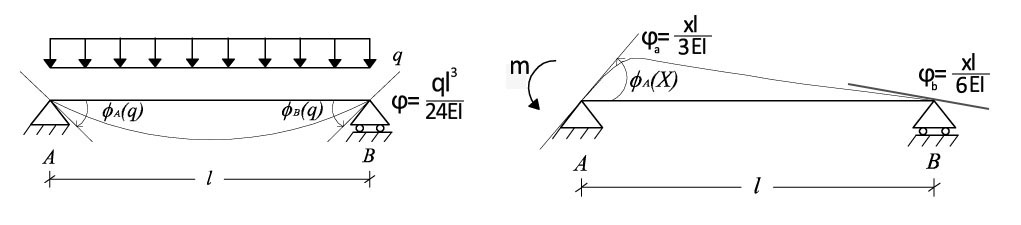
-Impongo che in A-B-C la rotazione di destra sia uguale alla rotazione di sinistra e le pongo uguali a 0
Δϕ(B) = 0 => ϕ sx(B) - ϕ dx(B) = 0
Δϕ(C) = 0 => ϕ sx(C) - ϕ dx(C) = 0
Δϕ(D) = 0 => ϕ sx(D) - ϕ dx(D) = 0
• Δϕ(B) = 0
ϕ sx(B) = ql³/24EI - X1l/3EI
ϕ dx(B) = - ql³/24EI + X1l/3EI + X2l/6EI
=> ql³/24EI - X1l/3EI + ql³/24EI - X1l/3EI - X2l/6EI = 0
• Δϕ(C) = 0
ϕ sx(C) = ql³/24EI - X2l/3EI - X1l/6EI
ϕ dx(C) = - ql³/24EI + X2l/3EI + X3l/6EI
=> ql³/24EI - X2l/3EI - X1l/(6EI ) + ql³/24EI - X2l/3EI - X3l/6EI = 0
• Δϕ(D) = 0
ϕ sx(D) = ql³/24EI - X3l/3EI - X2l/6EI
ϕ dx(D) = - ql³/24EI + X3l/3EI
=> ql³/24EI - X3l/3EI - X2l/6EI + ql³/24EI - X3l/3EI = 0
4. Risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche
ql³/12EI - 2X1l/3EI - X2l/6EI = 0
ql³/12EI - X1l/(6EI ) - 2X2l/3EI - X3l/6EI = 0
ql³/12EI - X2l/6EI - 2X3l/3EI = 0
=> RISOLVO IL SISTEMA =>
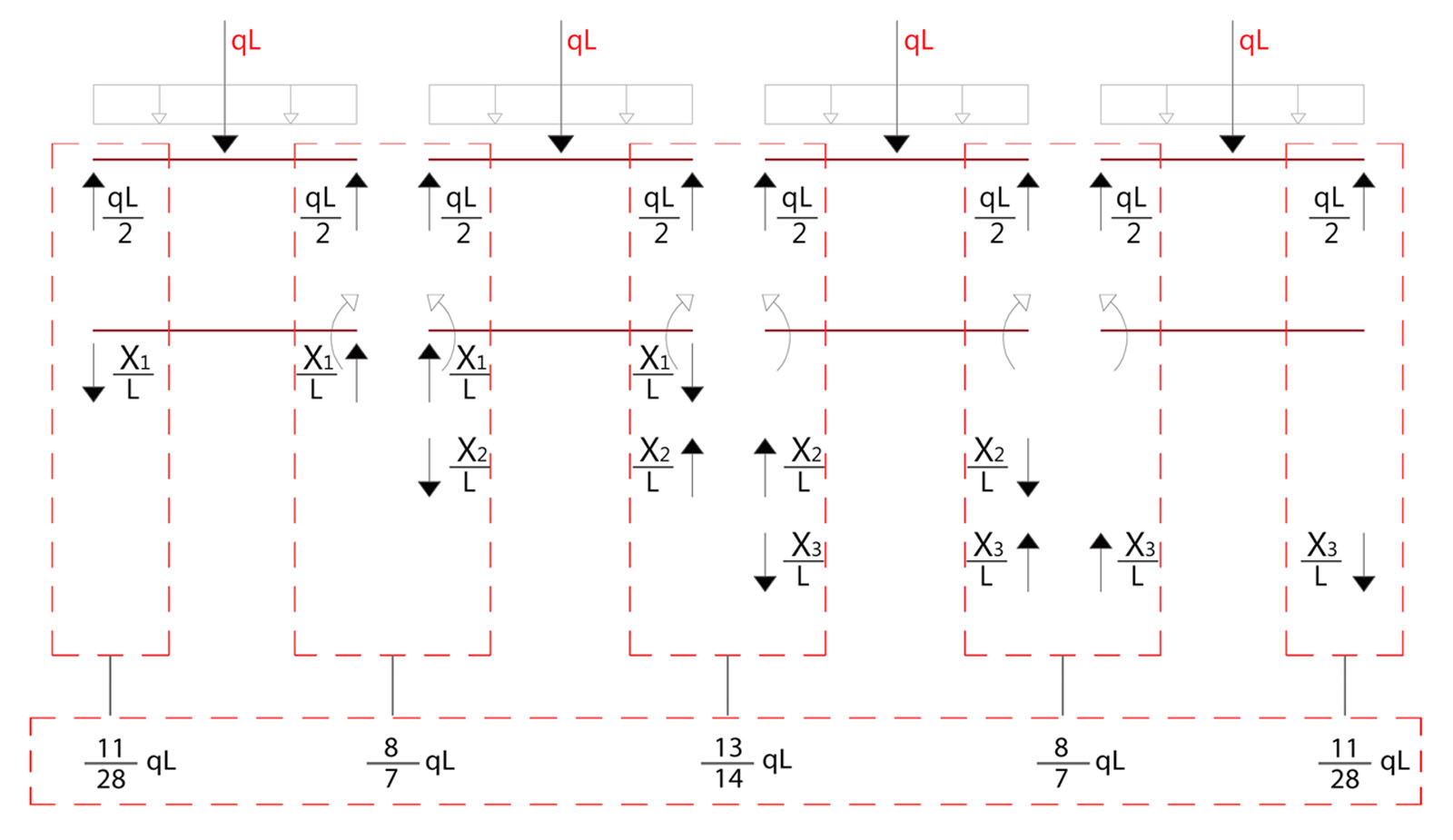
X1 = 3/28 ql²
X2 = 1/14 ql²
X3 = 3/28 ql²
5.Applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica
6.Diagramma del taglio e del momento e reazioni vincolari
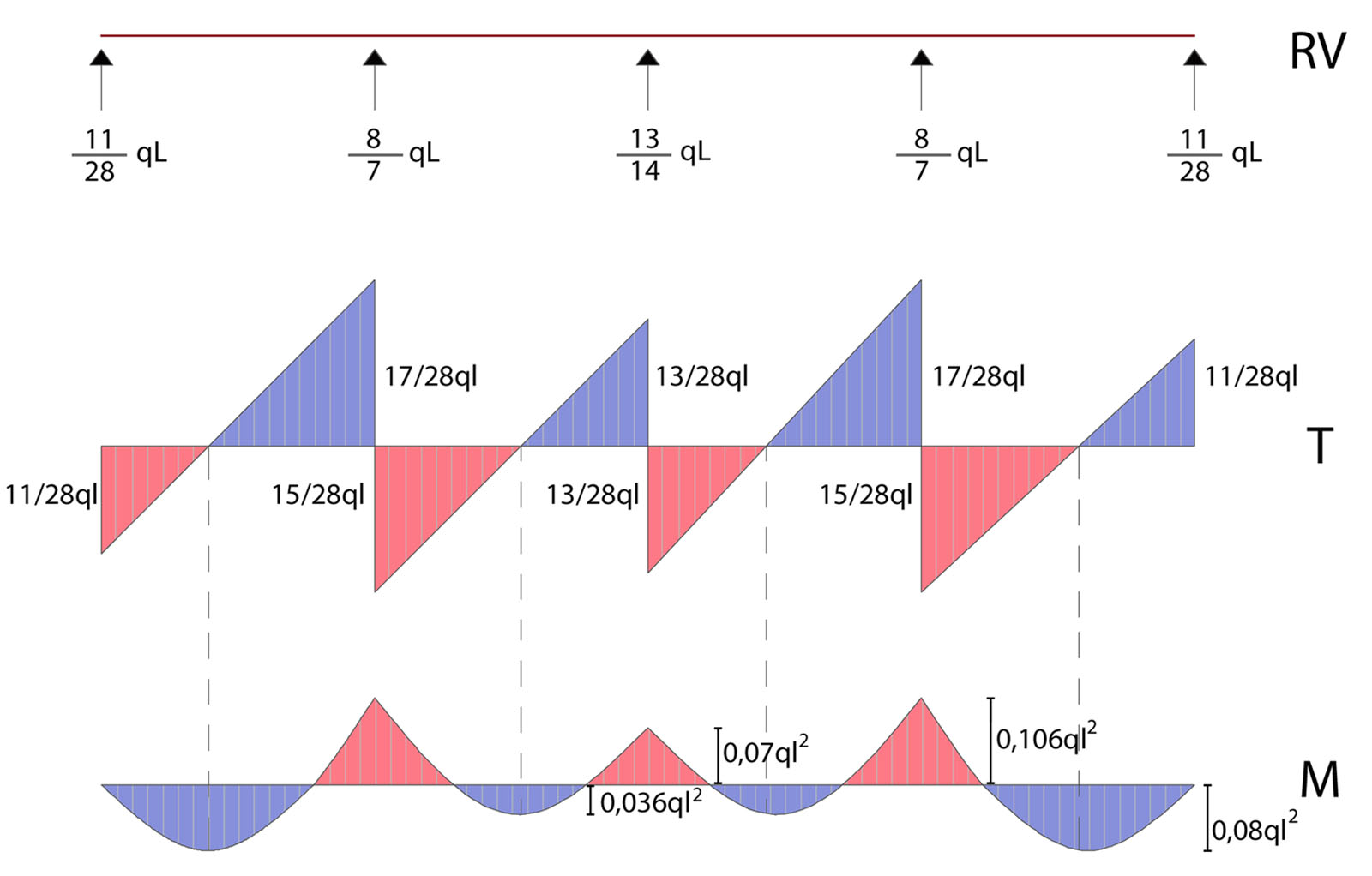
M max(11/28l) = 11/28 ql . 11/28 l- (q(11/28 l)^2)/2 = 0,08ql²
M max(11/28l) = 15/28 ql . 15/28 l- (q(15/28 l)^2)/2- 3/28 ql² = 0,036ql²
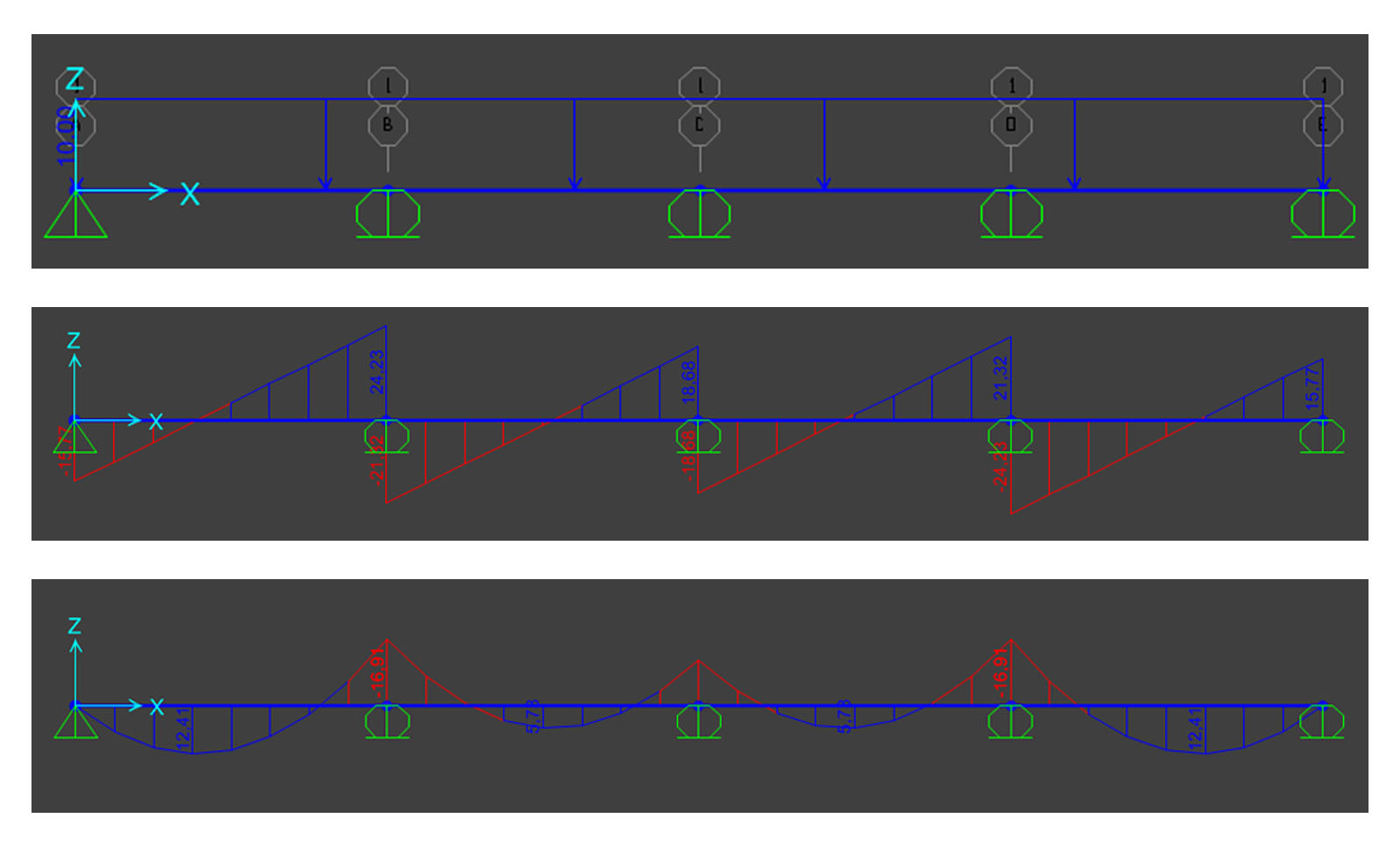
7.Verifica in SAP 2000
-Assegnando una luce pari a 4m ed un carico distribuito pari a 10KN/m otterremo i seguenti diagrammi di taglio e momento