esercitazione 6_Mensola Vierendeel

Inviato da erica.agnelli il Mar, 07/05/2013 - 15:30

Esercitazione 6

Metodo delle rigidezze – Mensola Vierendeel

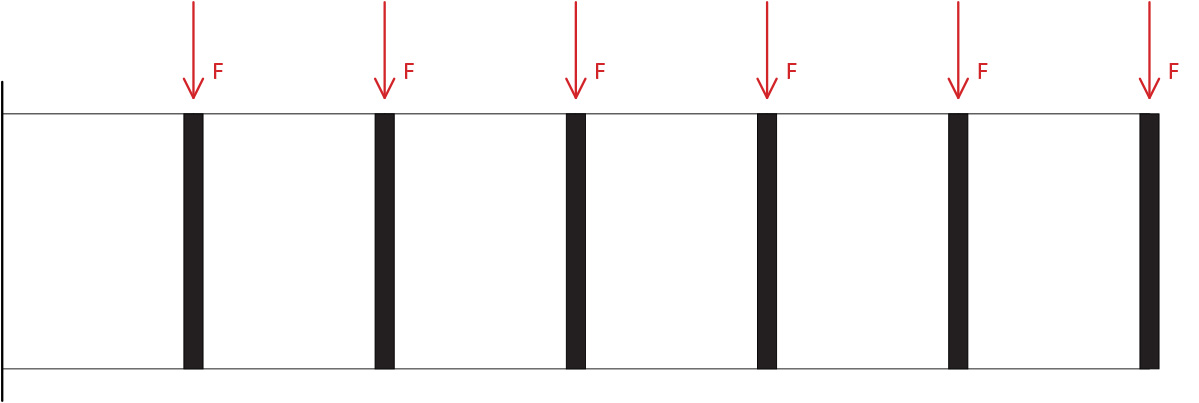
Lo schema di mensola Vierendeel qui sopra disegnato presenta un’analogia  (come già sottolineato nel caso della trave Vierendeel doppiamente incastrata) con il telaio shear type, progettato a forze orizzontali.

Fatta questa premessa e ipotizzando che il corrente inferiore e quello superiore abbiano pari rigidezza, risulta chiaro che questi sopportino in egual misura i carichi verticali a cui la trave è soggetta, da cui  si ottengono le seguenti reazioni vincolari ed i conseguenti valori del taglio:

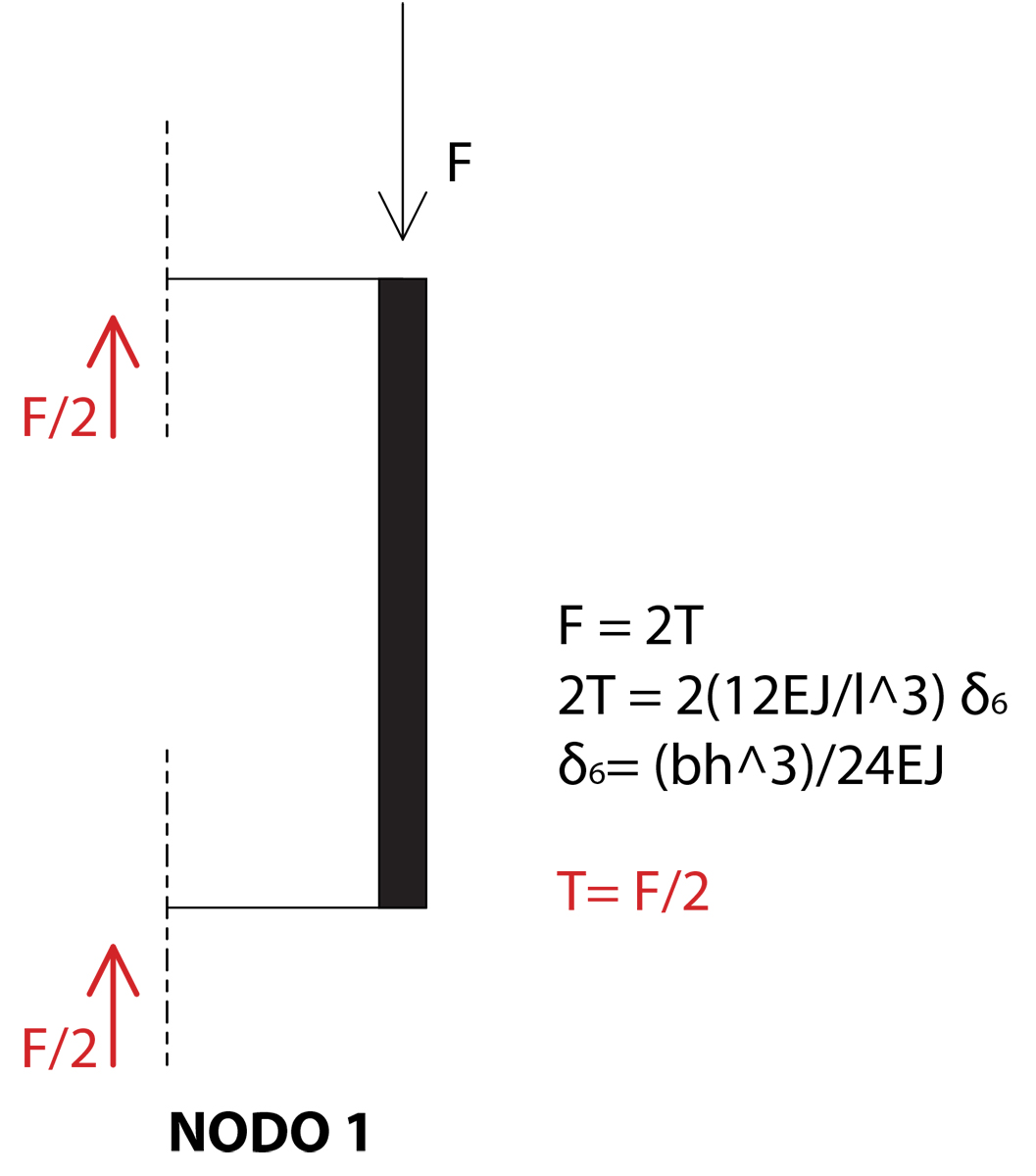
Sempre per analogia con il telaio shear type, possiamo aspettarci che il diagramma del momento abbia un nullo a metà dei traversi e che abbia un andamento lineare. Troviamo quindi un altro valore che ci permetta di disegnare la retta “passante per due punti” che costituisce la legge del momento. Troviamo così il valore del momento con polo in L/2 per capire il valore del momento in 0 ed L.

M(0) = (F/2)*l/2 = Fl/4

Lo stesso calcolo viene effettuato per tutti i tratti, essendo così finalmente in grado di disegnare il seguente diagramma del momento:

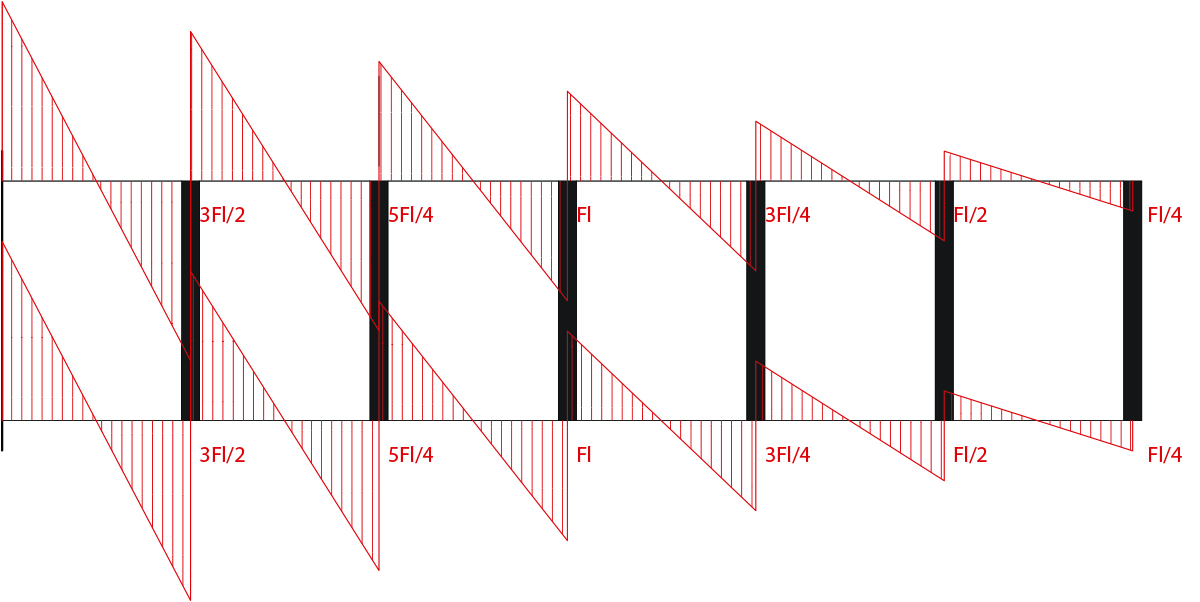
Tramite l’analisi dell’equilibrio dei nodi possiamo poi arrivare a definire i diagrammi del momento dei ritti:

Una volta ottenuti tali valori, si può arrivare anche quelli del taglio, tramite l’analogia fra momento applicato e coppia di forze posta a opportuna distanza.

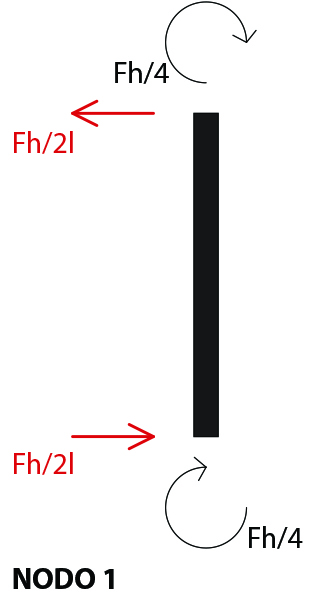
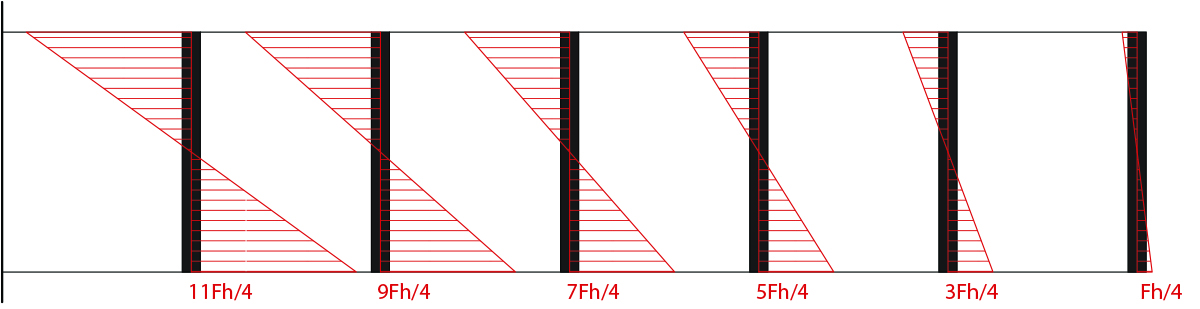
Si può così disegnare il seguente grafico del taglio:

Osservando poi che in un corpo continuo gli sforzi di taglio in un tratto diventano sforzi normali per i tratti ortogonali adiacenti, possiamo disegnare anche la legge dello sforzo normale per i traversi:

Possiamo infine ricavare gli spostamenti verticali dei ritti tramite la relazione T=(12EJ/l3)δ

F/2 = T = ((12*E*J)/L³)*δ1

δ1= (F*L³) / (1/24*E*J)

 

F = T = ((12*E*J)/L³)*δ2

 δ2= (F*L³) / (1/12*E*J)

 

F*3/2 = T = ((12*E*J)/L³)*δ3

δ3= (F*L³) / (1/8*E*J)

 

F*2 = T= ((12*E*J)/L³)*δ4

δ4= (F*L³) / (1/6*E*J)

 

F*5/2 = T = ((12*E*J)/L³)*δ5

δ5= (F*L³) / (1/24*E*J)

 

F*3 = T= ((12*E*J)/L³)*δ6

δ6= (F*L³) / (1/4*(E*J)