Costruzione del nodo del British Museum

Riepilogo i ragionamenti fatti sul nodo in questione.

Le braccia del nodo variano facendo variare anche l'angolo di direzione delle aste che ospitano, ho modellato il nodo in 2d avente come variabili solo le lunghezze delle 6 braccia. In questo modo posso ricavare la direzione delle aste che si incontrano nel nodo, sapendo che, è data dal segmento tra il centro del nodo e il punto medio della linea congiungente le due braccia.

seguendo questo procedimento per tutte le braccia si può notare che cambiando le lunghezze di queste automaticamente variano anche gli angoli delle direzioni delle aste.

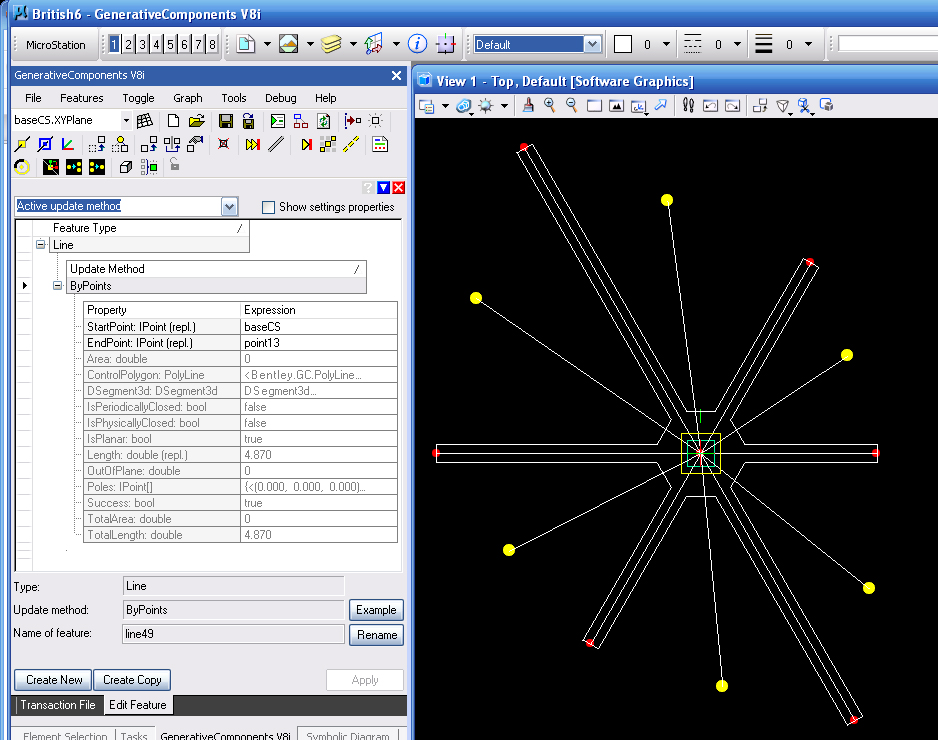
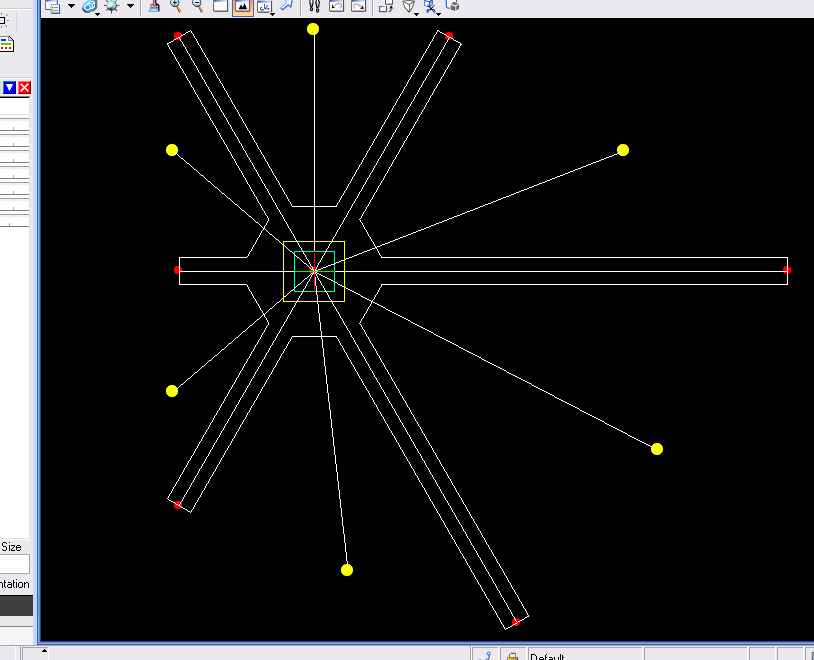
A questo punto però va fatto un ragionamento inverso. In teoria il punto di partenza non è il nodo ma la superficie alla quale vanno applicati i vari nodi con le aste. Le superfici infatti possono avere qualsiasi forma e quindi sta al nodo a modellarsi in base a questa. Attraverso GC è possibile "pannellare" una qualsiasi superficie con una griglia di punti su questa. Avendo in questo modo una serie di poligoni triangolari. Ogni spigolo dei poligoni corrisponde ad un'asta della struttura. Quindi le direzioni degli spigoli devono coincidere con le direzioni delle aste trovate dai nodi.

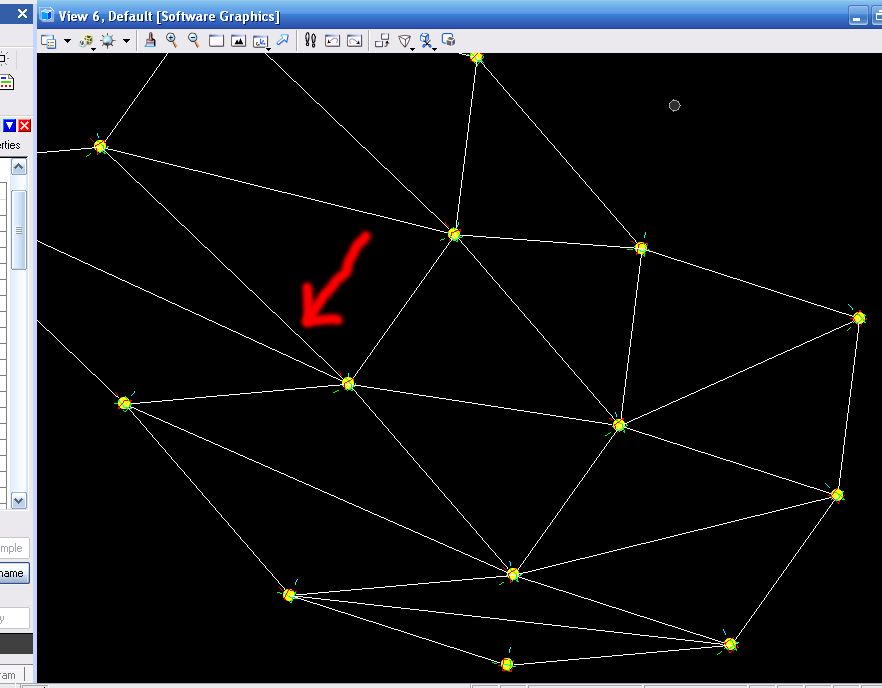
Detto ciò ho dovuto rimodellare il nodo poichè il punto di partenza deve essere la direzione delle aste ed il nodo deve trasformarsi di conseguenza variando automaticamente le lunghezze dei bracci. Il procedimento in questo caso non è stato molto semplice ed ho dovuto fare ulteriori studi sul piano geometrico del nodo.

Sono partito dalla considerazione che il nodo ha forma esagonale nel caso in cui tutte le braccia siano uguali. Gli angoli tra queste sono quindi di 60° e quindi l'angolo delle direzioni in riferimento ad un braccio è di 30°

α1 = α2 = 30°

in questo caso il triangolo formato dalle 2 braccia c ed il segmento che le unisce 2a è equilatero. Quindi conoscendo h:

c = h/cos(α2) 

inoltre posso calcolare l'area A del triangolo ahc:

A = (h*c*sen(α2))/2

ipotizzando ora che l'angolo α2 si riduce, il nodo assume una forma di questo tipo:

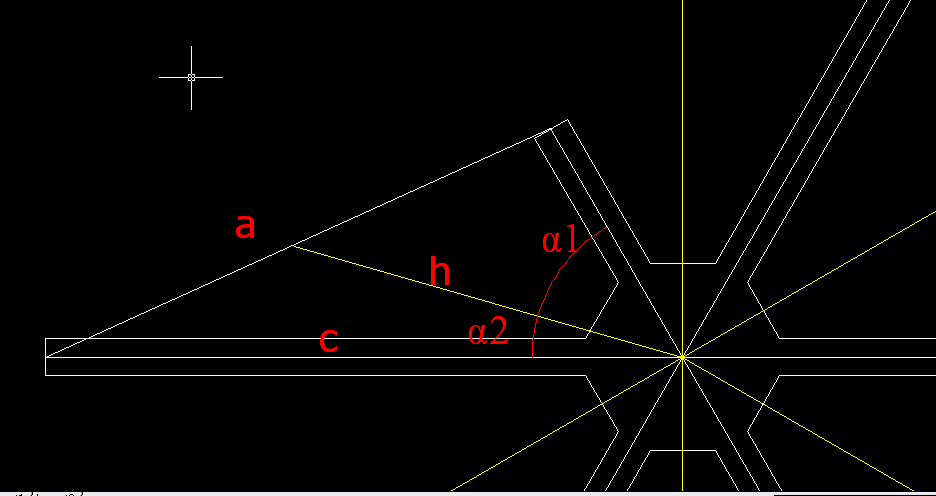
 h ed A rimangono uguali, bisogna calcolare la lunghezza di c conoscendo anche il nuovo angolo α2':

c' = (2*A)/(h*sen(α2'))

questo è quindi il nodo con le sue variabili e formule: