Tesi master theses
Devoto fabrication partner
CNC: real experiences | case studies
Acoustics projects | form | analisys
Custom Families Revit
Data Production model to data
Visual Basic scripting for Revit
Barrisol project for a conferece hall
Eccoci nella terza parte del tutorial.
Qui vedremo come generare una struttura reticolare attraverso la mappatura di una superficie.
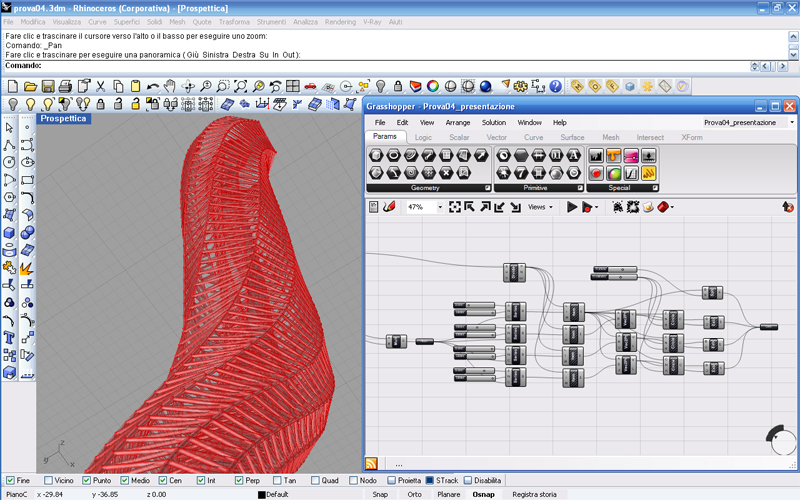
Eravamo rimasti alla nostra superficie Loft sopra la quale vogliamo adesso applicare la nostra struttura. Come prima cosa dobbiamo suddividere la nostra superficie orizzontalmente e verticalmente in modo da ottenere una griglia a maglia rettangolare (o quadrata se vogliamo) che sarà la nostra matrice per posizionare i nostri elementi metallici che semplificheremo con cilindri e sfere.
Per ottenere ciò inseriamo il comando Divide Interval2, un comando molto potente quanto semplice: presenta 3 entrate, la prima è la superficie di base da suddividere e le altre due sono le coordinate U V ossia il numero di divisioni lungo l’asse U e quello lungo l’asse V che praticamente sono le coordinate intrinseche di una superficie, come X e Y. Quindi nella prima inseriamo la nostra Loft e nelle altra due uno Slider con numeri a nostro piacimento. Un’accortezza: Per quanto riguarda le coordinate U (quelle che determinano lo sviluppo in verticale) c’è da considerare il fatto che normalmente una struttura esterna a un edificio segue quasi sempre i solai interni, cioè un nodo strutturale non sarà situato a caso suddividendo ad esempio l’altezza dell’edificio in 40 parti quando magari (come nel nostro caso) l’edificio ha 60 piani; questo equivarrebbe ad avere dei nodi tra le finestre e questo noi vogliamo evitarlo, quindi dobbiamo trovare un modo per parametrizzare la coordinata U in modo da essere un sottomultiplo del numero dei piani.
Ecco come:
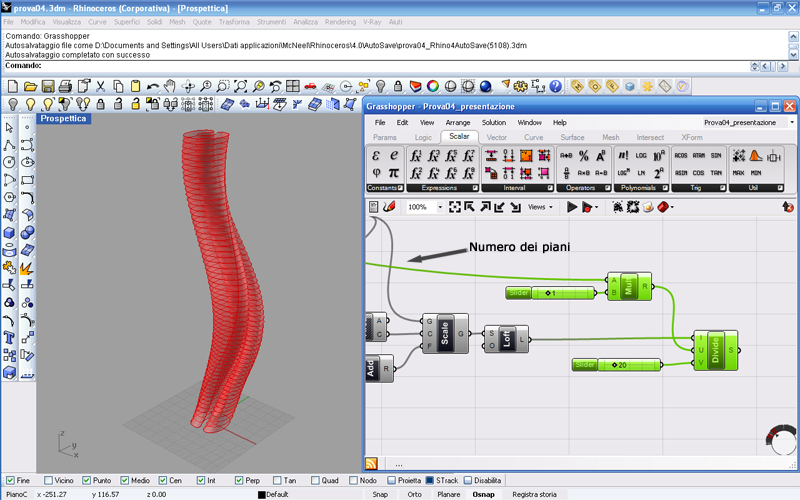
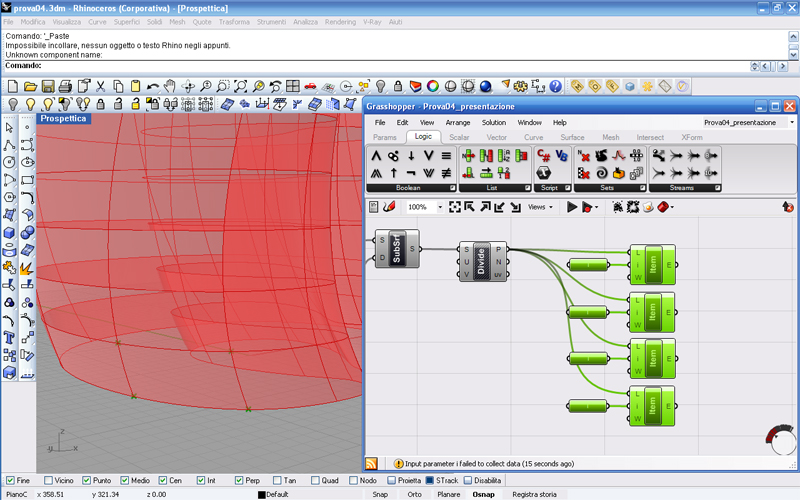
Come vediamo ho usato il moltiplicatore Multiple per moltiplicare il numero di piani a uno slider di numeri interi impostato su 1 in modo di avere una suddivisione per ogni piano; come suddivisione lungo V ho messo un numero a caso, 20.
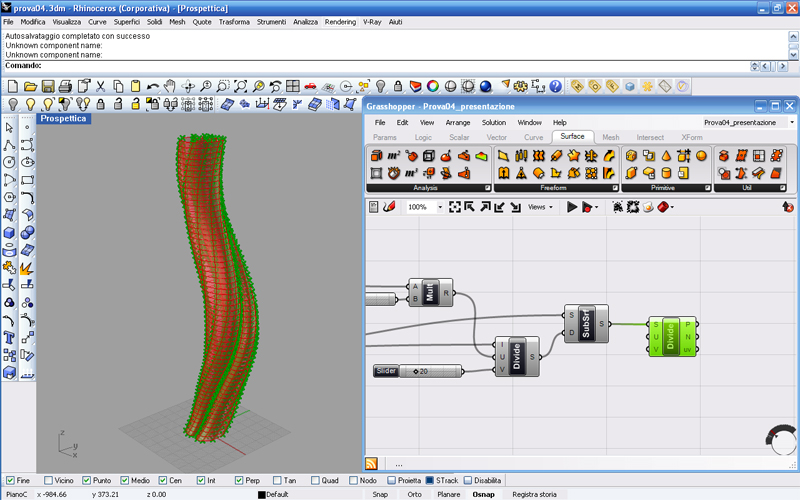
Ancora non vediamo niente perché abbiamo solo fatto una suddivisione teorica; quindi adesso utilizziamo l’Isotrim per generare una nuova superficie coincidente con la precedente, ma composta da tanti piccoli pezzettini corrispondenti alla nostra griglia.
Inserito l’Isotrim colleghiamo la prima entrata che come sempre mi chiede la geometria di base da suddividere con il nostro solito Loft, e la seconda entrata che vuole sapere il dominio di suddivisione con il comando Divide. Spegniamo i precedenti comandi ed avremo un risultato di questo tipo:

Abbiamo ottenuto una griglia 20x60 e adesso vogliamo che ad ogni incrocio ci sia una sfera e ogni segmento abbia un cilindro. Ma da bravi architetti sappiamo che una maglia quadrata non è molto resistente, quindi andiamo a posizionare un cilindro anche sulla diagonale. Il procedimento è un po' complicato, ma andiamo a vedere qual è!
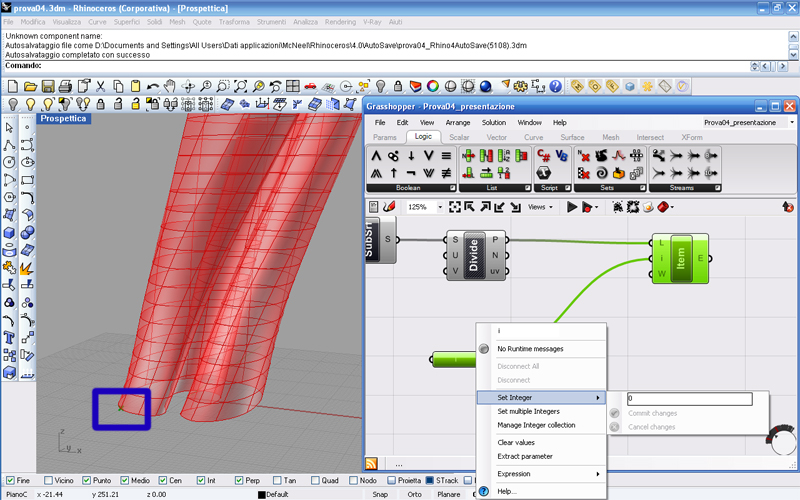
Cominciamo coll’individuare tutte le intersezioni della griglia e lo facciamo utilizzando il comando Divide Surface sotto il menu Surface. Colleghiamo l’uscita della nostra Isotrim con il comando nuovo ed avremo automaticamente tutti i punti della griglia segnati con una X.
Adesso però dobbiamo riuscire ad individuare il primo punto della griglia, pertanto inseriamo un nuovo comando: List Item, che in poche parole estrae un elemento specifico da una lista. Colleghiamo la prima uscita di Divide Surface, che mi da tutti i punti della lista, alla prima entrata di List Item, che richiede per l’appunto una lista di base. La seconda e la terza uscita di Divide Surface non ci interessa al momento, ma per conoscenza la seconda mi dà le normali dei punti e la terza le coordinate UV dei punti.
Togliamo l’anteprima da Divide Surface per trovare più facilmente il punto 0. Clicchiamo col destro sopra l’entrata “i” di List Item, che mi chiede proprio quale numero della lista prendere, ci apparirà il menu a tendina e clicchiamo su Extract Parameter. Automaticamente uscirà già collegato al comando un parametro di numeri interi che andremo a settare nel seguente modo: click col destro sopra al parametro appena spuntato, andiamo col cursore sopra Set integer ed inseriamo il numero 0, che sarebbe il primo numero della lista. Diamo invio e magicamente apparirà una sola X sul disegno che corrisponderà al nostro punto primo della griglia.
Allo stesso modo individuiamo il punto 2 copiando e incollando i comandi List Item e Integer e mettendo 1 al nuovo set integer 1.

Di nuovo altre due volte settando l’integer rispettivamente a 2 e a 3 e otterremo una cosa del genere:
Vediamo che quindi i primi 4 numeri della lista formano proprio un quadrato e noi per formare la nostra griglia andremo a collegare il punto 0 col punto 1, col punto 2 e col punto 3.
Per fare una prova colleghiamo questi punti con delle semplici linee, quindi inseriamo il comando Line, sotto il menu curve, e nel primo input A attacchiamo il punto 0, mentre nel secondo B il punto 1. Inseriamo una seconda linea e stavolta le colleghiamo il punto 0 e 2. Infine l’ultima linea col punto 0 e 3.

Vediamo che tutto funziona per il meglio, il che è importante perché bisogna sempre fare un passo per volta e vedere se quello che stiamo facendo funziona prima di fare passi più complicati. Infatti ora dovremo compiere passi più ardui!!!
Con questo metodo saremmo costretti per terminare la sequenza di linee a copiare e incollare 3600 volte il comando Item, cosa non molto pratica dal momento che stiamo usando un plug-in parametrico e quindi che sarebbe da sfruttare come tale. Pertanto dovremmo creare una serie che sia in grado di muoversi dentro la griglia in maniera sequenziale facendo il lavoro ripetitivo al posto nostro.
Per fare ciò ovviamente inseriamo il comando Series e lo sostituiamo al vecchio integer. Il comando Series lo avevamo già visto nel tutorial precedente, ma adesso lo utilizzeremo in una maniera un po' più spinta: la prima entrata S come sapevamo mi chiede il primo numero della serie e noi immettiamo uno slider di numeri interi che vanno da 0 a 3 e lo impostiamo su 0; poi sulla seconda entrata N che vuole sapere il passo per ogni numero successivo inseriamo sempre uno slider di numeri interi che vanno da 0 a 4 e lo impostiamo su 4; nell’ultima entrata C che mi chiede quanti sono i numeri totali della serie metteremo uno slider sempre di numeri interi settato su 1200. Facciamo questo per tutti i List Item, con l’unica accortezza di cambiare il primo valore rispettivamente in 1, 3 e 2.
Otterremo una cosa di questo tipo:

Ma cosa abbiamo fatto? In poche parole abbiamo suddiviso virtualmente la griglia in step di 4 punti, infatti il secondo slider della serie era proprio impostato su 4, dopodiché abbiamo detto che per ogni step bisognava disegnare una linea da 0 a 1, da 0 a 2 e da 0 a 3; questo l’abbiamo fatto assegnando il primo valore della serie una volta a 0, poi a 1, 2 e 3. Quindi ogni serie di ogni List Item ha un’identità, come l’aveva prima, solo che adesso l’identità vale per ogni step fino a quello finale che è impostato su 1200 che sono i punti totali della griglia (60x20).
A tal proposito vorrei precisare che l’aver messo uno slider a 1200 non è stata una scelta intelligente, ma solo rapida. Infatti come ho già detto il 1200 si riferisce al totale dei punti presenti nella griglia 60x20, ma questa griglia è determinata da due parametri che potrò modificare a mio piacimento in un secondo momento. Quindi il loro prodotto potrà modificarsi nel tempo e tale modifica non ricadrà nello slider 1200. Quindi andiamo a correggere questa imprecisione sostituendo allo slider una moltiplicazione Multiplication, dove al primo membro metteremo il parametro 60, però quello che abbiamo usato per la griglia, quindi quello che esce dalla moltiplicazione col fattore 1 e al secondo membro mettiamo il parametro 20. Bene, ma questo non basta, perché se collegassimo la moltiplicazione direttamente alla serie troveremmo un errore perché l’uscita della moltiplicazione non è un numero, quindi la faremo filtrare dal parametro Number.
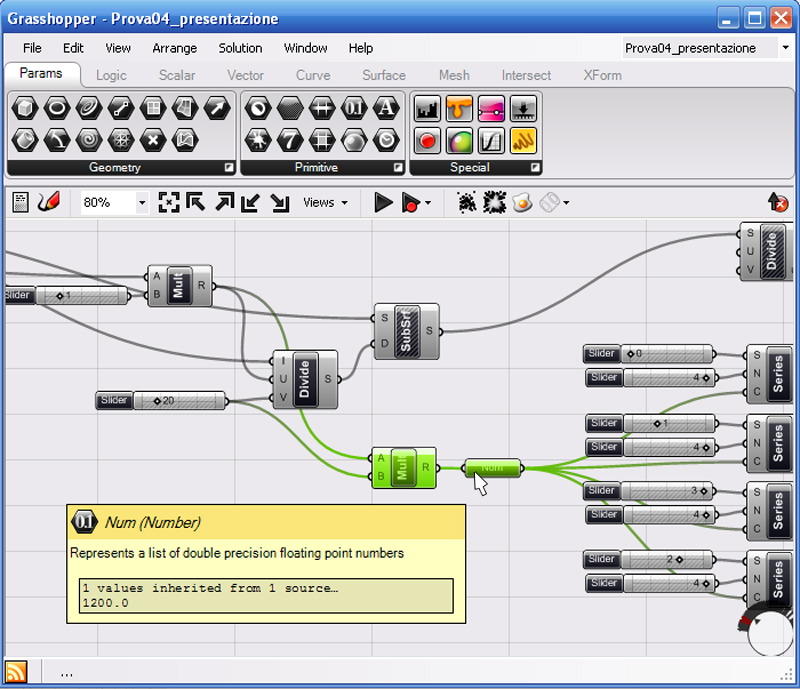
Notiamo anche che passando col cursore sopra il parametro Number si aprirà temporaneamente un pop-up che ci informerà che il numero di uscita sarà proprio il nostro 1200.
Tornando a noi… ora però, noi non vogliamo delle linee, ma delle sfere e dei cilindri.
Per cominciare eliminiamo le linee e togliamo l’anteprima dei List Item. Poi ci creiamo subito i parametri per il raggio della sfera e quello dei cilindri inserendo due slider.

A questo punto sorge un piccolo problema: non esiste un comando cilindro che mi permetta di dargli 2 punti estremi e il raggio. Infatti se vediamo il comando Cylinder sotto il menu surface, notiamo di aver bisogno del piano di base, del raggio e dell’altezza, quando noi abbiamo solo uno dei tre, ossia il raggio. Non conosciamo per ogni punto il piano di base necessario per generare un cilindro che vada da un punto a un altro in una superficie tanto complessa, e per determinare l’altezza di ogni elemento servirebbe un lavoro molto lungo e tempi di calcolo molto elevati. Quindi è stato necessario trovare un’alternativa migliore e vincente, la seguente: invece di generare un cilindro possiamo banalmente disegnare un cerchio e successivamente estruderlo. Questo ci permetterà di aver bisogno solamente di un vettore che vada da punto a punto, cosa ben più semplice di ciò di cui si parlava prima.
Quindi, cominciamo col determinare i vettori principali andando sotto al menu Vector e trascinando l’icona di Vector2Pt (vettore passante per due punti) nell’area di lavoro. Il comando è molto semplice, basta inserire in A il primo punto e in B il secondo, sapendo che il vettore avendo una direzione terrà in considerazione l’ordine dell’immissione dei punti. In realtà c’è un altro parametro da poter settare in Vector2Pt, sarebbe U (Unitize Output) che praticamente può essere impostato su true o su false per ottenere un risultato unificato o differenziato, una sorta di unione booleana; di default è impostato su false e lasciamolo così.
Ne dobbiamo inserire 3, perché abbiamo bisogno di 3 vettori, da 0 a 1, da 0 a 2 e da 0 a 3. Molto semplicemente colleghiamo i rispettivi Item con le apposite entrate del vettore.
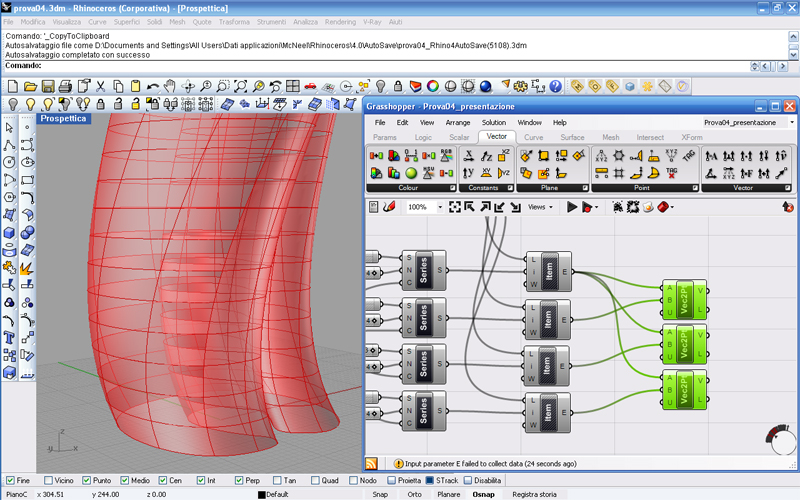
Non vediamo nessun risultato perché Grasshopper non ci fa vedere i vettori. Ma adesso andiamo a inserire i primi cilindri.
Andiamo nel menu Curve e trasciniamo l’icona del Circle CNR (cerchio definito dal centro, vettore normale e raggio) nell’area di lavoro. Come centro gli diamo il primo Item, come normale il primo vettore e come raggio il parametro precedentemente creato.
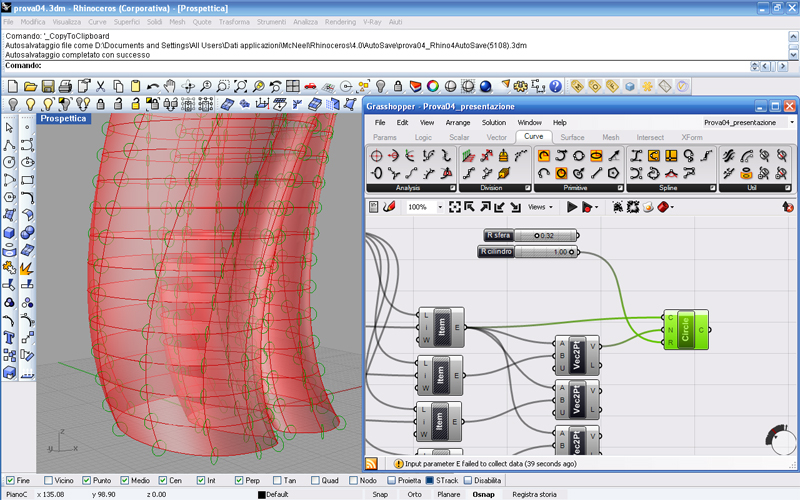
Vediamo che abbiamo creato un cerchio per ogni punto orientato secondo il primo vettore che andando dal punto 0 al punto 1 sarà un vettore parallelo al terreno, quindi il risultato ottenuto è giusto.
Adesso dobbiamo estrudere questi cerchi usando il comando Extrude sotto Surface. Inseriamo la curva da estrudere e il vettore d’estrusione e il risultato sarà il seguente:
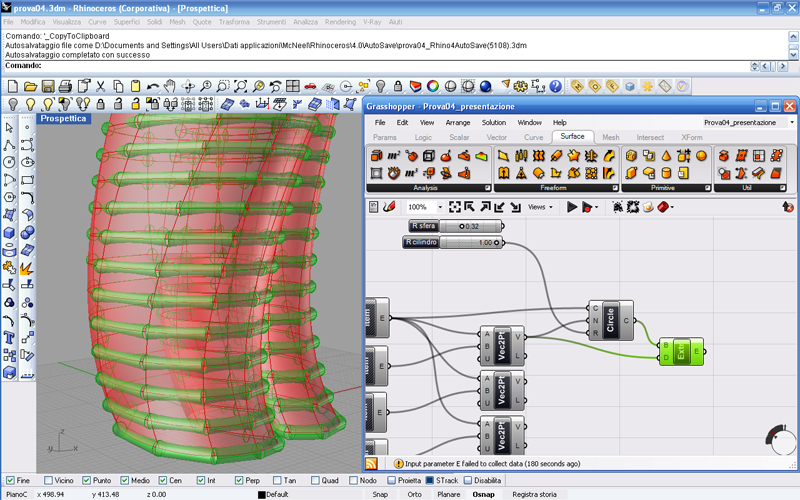
Riduciamo un po' il raggio dei cilindri evidentemente troppo grandi.
Ripetiamo il procedimento inserendo un altro cerchio con centro sempre in 0, quindi il primo Item, come vettore normale adesso prendiamo il secondo vettore e il raggio resta sempre sempre lo stesso.
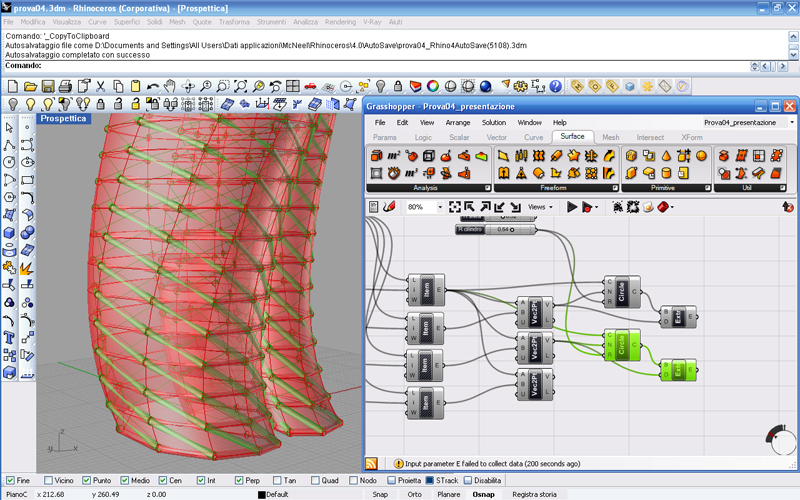
Di nuovo, stavolta mettendo l’ultimo vettore sia al cerchio che all’estrusione.

Ora invece andiamo a mettere le sferette leggermente più grandi dei cilindri. Questo passaggio sarà davvero facilissimo.
Inseriamo il comando Sphere una volta sola, colleghiamo la prima entrata che mi chiede il centro della sfera con l’Item 0, poi colleghiamo la seconda entrata che mi chiede il raggio col parametro apposito.
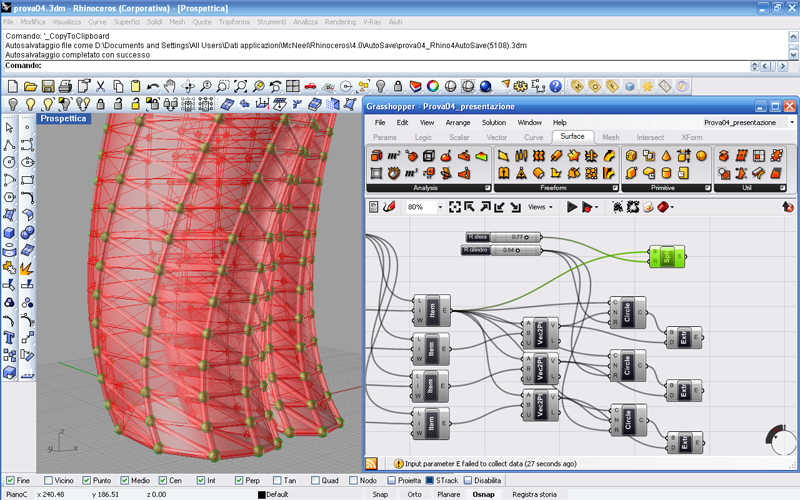
Adesso andiamo a nascondere il nostro Isotrim iniziale per ammirare la struttura nella sua totalità, poi regoliamo bene i raggi dei cilindri e delle sfere e otteniamo una struttura completamente parametrizzata.
A questo punto mi verrebbe da unire tutte le geometrie in una unica. Per fare questo spegniamo le anteprime di tutto ciò che vediamo, quindi i cerchi, le estrusioni, le sfere, etc. ed uniamo i cilindri e la sfera al nuovo parametro geometry.
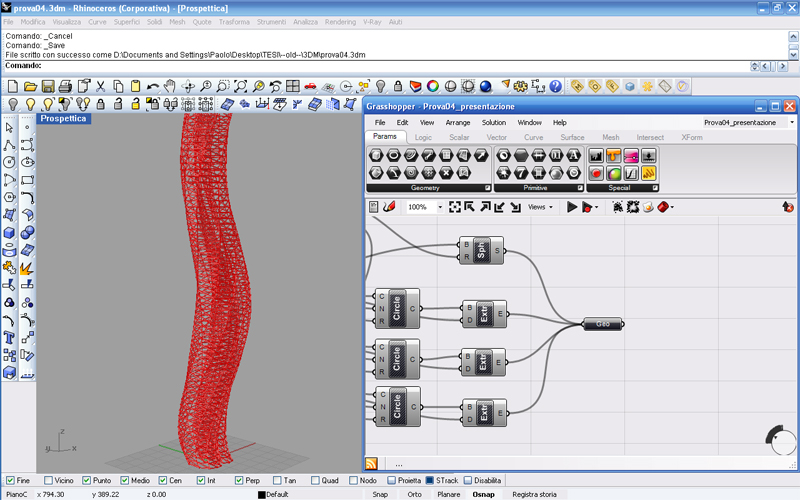
Commenti recenti