
- Progetto un impalcato di riferimento come in figura: posiziono travi, pilastri e scelgo le orditure dei solai.
- Calcolo le aree di influenza per ogni trave principale, sapendo che il solaio posto sopra scarica il peso perfettamente sulle due travi principali dalle quali è sorretto.
- Riconosco la trave mensola maggiormente sollecitata con area di influenza pari al prodotto tra la luce e l’ interasse. (3mx6m= 18m2)
A questo punto bisogna trovare il peso totale che il solaio scarica su un m2 di trave tenendo in considerazione i 3 carichi che agiscono: Qs carico strutturale, dato dal peso della struttura, Qp sovraccarico permanente, dato da quegli elementi che permanentemente compongono il solaio (incidenza impianti, incidenza tramezzi, intonaco, pavimento ecc..) e Qa sovraccarico accidentale valore fisso in base alla destinazione d’uso dell’ efidicio, dato dalla norma NTC (d.m. 14.01.2008).
Adesso andiamo a calcolare la nostra struttura con i tre materiali:
CALCESTRUZZO ARMATO
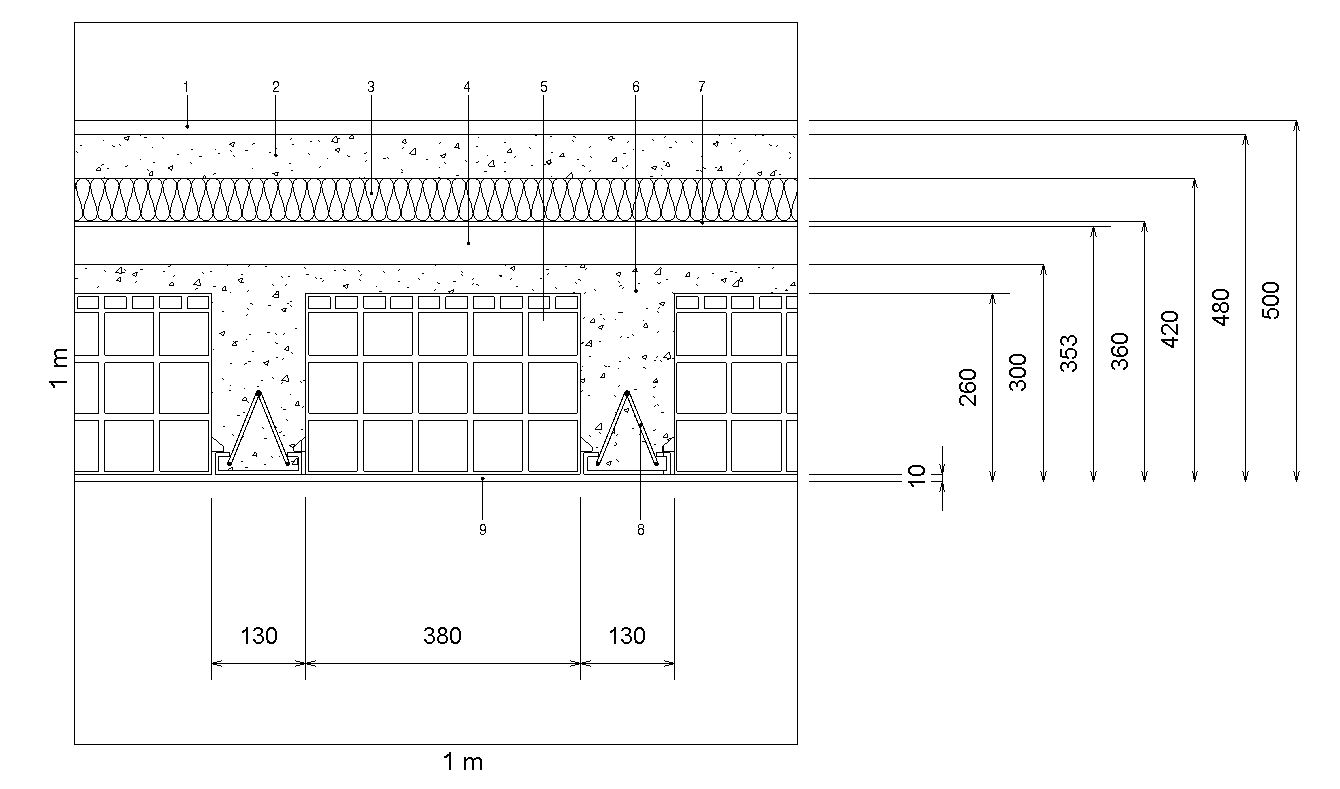
- Pavimentazione - 2cm
- Malta di allettamento - 4cm
- Isolante - 6cm
- Guaina impermeabile – 0,7cm
- Caldana - 4cm
- Piagnatta - 26x38x20cm
- travetti - 13cm
1- CARICO STRUTTURALE (Qs)
Calcolo il carico strutturale in un m2 di solaio dato dalla somma del carico dato dai travetti, elementi strutturali del solaio e dalle pignatte, di alleggerimento.
I(travetti)= interasse= 0,50m
I(pignatte)= 0,38m
Numero di travetti in un metro2 = 1/i = 2
Numero di pignatte in un metro2 = 1/i = 2,63
Calcolo il peso dei singoli materiali moltiplicando il Volume con il proprio peso e con il numero di elementi in un metro2:
Caldana = γ * V = 25 kN/m3 * (0,04*1*1)m = 1 kN/m2
Travetti = 25 kN/m3 * 2* (0,26*0,13*1)m = 1,69 kN/m2
Pignatte = 5,5 kN/m3 * 2,63* (0,26*0,38*1)m = 1,42 kN/m2
Qs tot = 1 kN/m2 + 1,69 kN/m2 + 1,42 kN/m2 = 4,11 kN/m2
2- CARICO PERMANENTE (Qp)
Calcolo il sovraccarico permamente in un m2 di solaio dato dalla somma del peso degli elementi portati permamentemente:
Intonaco = 15 kN/m3 * (0,01*1*1)m = 0,15 kN/m2
Malta di allettamento = 20 kN/m3 * (0,04*1*1)m = 0,8 kN/m2
Isolante =
Pavimento = 28 kN/m3 * (0.01*1*1)m = 2,28 kN/m2
Incidenza impianti = 0,5 kN/m2
Incidenza tramezzi = 1 kN/m2
Qs tot = 0,15 kN/m2 + 0,8 kN/m2 + 0,03 kN/m2 + 2,28 kN/m2 + 0,5 kN/m2 + 1 kN/m2 = 4,76 kN/m2
3- CARICO ACCIDENTALE (Qa)
2,00 kN/m2 à valore tabellato da normativa, dipendente dalla destinazione d’uso dell’ambiente architettonico preso in esame, in questo caso ho scelto di immaginare il solaio come interpiano di un edificio residenziale.
4- CALCOLO IL CARICO ULTIMO (Qu)
Qu = (1,3*qs + 1,5*qp + 1,5*qa)* i = (1,3 * 4,11 + 1,5 * 4,76 + 1,5 * 2)* 6 = 92,80 kN/m2
5- CALCOLO DEL MOMENTO MASSIMO
Poichè si sta prendendo in considerazione una mensola e non una trave appoggiata, il momento massimo sarà uguale a qL2/2
Mmax= 4,76 * 5^2/8= 290,31 KN*m
6- SCELGO LA CLASSE DI RESISTENZA DELL’ ACCIAIO
Per l’acciaio da calcestruzzo armato sono previste solo due categorie B450A e B450C che hanno lo stesso valore di tensione di snervamento fyk=450 N/mm2 ma una differente duttilità cioè si rompono a seguito di due diverse deformazioni e perciò sono associate a due diversi coefficienti di sicurezza.
Scelgo l’acciaio B450C più duttile ammesso in zona sismica che ha un coefficiente di sicurezza più basso pari 1,15.
7- TENSIONE DI PROGETTO DELL’ ACCIAIO
fyd= fy/γs= 450/1,15 = 391,30 N/mmq
dove 1,75 è il coefficiente di sicurezza del calcestruzzo armato.
8- TENSIONE DI PROGETTO DEL CALCESTRUZZO
Le classi più usate sono la C20/25, C60/75 e la C40/50 come nel nostro caso. Inserisco il valore di resistenza cilindrica del calcestruzzo armato fck= 50N/mmq
fcd = 50/1,75= 22,67 N/mmq
dove 1,75 è il coefficiente di sicurezza del calcestruzzo armato.
9- ALTEZZA UTILE
A questo punto date le 2 incognite, trovo l’altezza della mia trave fissando un valore alla base b =30 cm, otteniamo così il valore di altezza utile hu che corrisponde alla distanza tra il lembo compresso della sezione e l’asse dell’armatura tesa.
Tramite il foglio Excel trovo prima il valore α e il valore r per determinare l’altezza utile:
β= fd_c/ (fd_c+fd_s/15)= 0.46 (numero puro); r = ( 2/( α ( 1- α/3)))^0.5= 2.26 (numero puro)
hu= r √(M/ fD_c x b) = 46,62 cm
L’altezza totale H=hu+δ = 46,62 +5 = 51,62 cm
dove δ è la misura del copriferro che di solito misura 5cm.
10- DEFORMABILITA’: STATI LIMITE D’ESERCIZIO (SLE)
Ci troviamo nel campo elastico, quindi dovremmo verificare che il rapporto tra la luce della mensola ed il suo spostamento sia maggiore di 250 come imposto dalla normativa. Per fare ciò, bisogna calcolare il momento di inerzia (b*h3)/12, bisogna ricalcolare il carico allo stato limite d’ esercizio [(Qs +Qp + 0.5*Qa) * interasse] + peso della trave in c.a. ed infine lo spostamento verticale massimo della mensola che come sappiamo è (qL4)/8EI. A questo momento verifico se il rapporto L/Vmax sia inferiore a 250 per accertarmi che la trave superi la prova a deformabilità a stato limite d’esercizio.
11- VERIFICA
Infine sommo al peso totale dei carichi il peso proprio della sezione della trave (2,00 kN/m2) e verifico se il profilo 20x40cm va bene o se ho bisogno di uno con un’ altezza maggiore.
La sezione 20x40 in c.a. è verificata.

ACCIAIO

1- CARICO STRUTTURALE (Qs)
Calcolo il carico strutturale in un m2 di solaio dato dalla somma del carico dato dalla lamiera gregata e dal getto di completamento
Calcolo il peso dei singoli materiali moltiplicando il Volume con il proprio peso e con il numero di elementi in un metro2:
Lamiera gregata = γ * V = 0,10 kN/m3 * (1*1*1)m = 0,10 kN/m2
Getto di completamento = 25 kN/m3 * (0,12*1*1)m = 3 kN/m2
Qs tot = 0,10 kN/m2 + 3 kN/m2 = 3,10 kN/m2
2- CARICO PERMANENTE (Qp)
Calcolo il sovraccarico permamente in un m2 di solaio dato dalla somma del peso degli elementi portati permamentemente:
Malta di allettamento = 20 kN/m3 * (0,03*1*1)m = 0,6 kN/m2
Rete elettrosaldata =
Pavimento = 28 kN/m3 * (0.01*1*1)m = 2,28 kN/m2
Incidenza impianti = 0,5 kN/m2
Incidenza tramezzi = 1 kN/m2
Qs tot = 0,6 kN/m2 + 0,54 kN/m2 + 2,28 kN/m2 + 0,5 kN/m2 + 1 kN/m2 = 4,92 kN/m2
3- CARICO ACCIDENTALE (Qa)
3,00 kN/m2 à valore tabellato da normativa, dipendente dalla destinazione d’uso dell’ambiente architettonico preso in esame, in questo caso ho scelto di immaginare il solaio come interpiano di un edificio per uffici.
4- CALCOLO IL CARICO ULTIMO
Qu = (1,3*qs + 1,5*qp + 1,5*qa)* i = (1,3 * 3,10 + 1,5 * 4,92 + 1,5 * 3)* 6 = 92,80 kN/m2
5- SCELGO LA CLASSE DI RESISTENZA
L’ acciaio scelto è del tipo FE430/ S375, il foglio excell mi calcola che il modulo di resisitenza minimo è Wx= 410,04 cm2 quindi devo necessariamente sceglie un profilato con modulo di resistenza maggiore:
IPE270 (Wx= 429cm2)
6- DEFORMABILITA’: STATI LIMITE D’ESERCIZIO (SLE)
Ci troviamo nel campo elastico, quindi dovremmo verificare che il rapporto tra la luce della mensola ed il suo spostamento sia maggiore di 250 come imposto dalla normativa. Per fare ciò, bisogna calcolare il momento di inerzia dato dalle tabelle delle IPE, bisogna ricalcolare il carico allo stato limite d’ esercizio [(Qs +Qp + 0.5*Qa) * interasse] + peso della trave in acciaio ed infine lo spostamento verticale massimo della mensola che come sappiamo è (qL4)/8EI. A questo momento verifico se il rapporto L/Vmax sia inferiore a 250 per accertarmi che la trave superi la prova a deformabilità a stato limite d’esercizio.
La trave di acciaio di tipo IPE 270 è verificata.

LEGNO
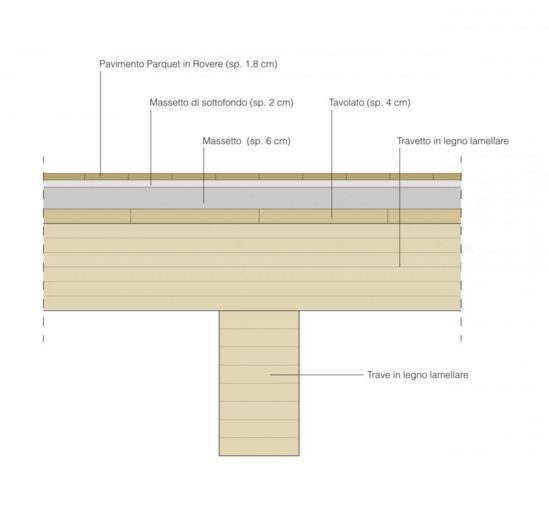
1- CARICO STRUTTURALE (Qs)
Calcolo il carico strutturale in un m2 di solaio dato dalla somma del carico dato dai travetti in legno e dal tavolato in legno
Calcolo il peso dei singoli materiali moltiplicando il Volume con il proprio peso e con il numero di elementi in un metro2:
travetti = γ * V = 5 kN/m3 * (0,20*0,40*1)m = 0,40 kN/m2
tavolato in legno = 6 kN/m3 * (0,04*1*1)m = 0,24 kN/m2
Qs tot = 0,40 kN/m2 + 0,24 kN/m2 = 0,64 kN/m2
2- CARICO PERMANENTE (Qp)
Calcolo il sovraccarico permamente in un m2 di solaio dato dalla somma del peso degli elementi portati permamentemente:
Caldana in cls = 20 kN/m3 * (0,04*1*1)m = 0,8 kN/m2
Malta di allettamento = 18 kN/m3 * (0,06*1*1)m = 1,08 kN/m2
Massetto di sottofondo =
Pavimento = 7,5 kN/m3 * (0,01*1*1)m = 0,07 kN/m2
Incidenza impianti = 0,5 kN/m2
Incidenza tramezzi = 1 kN/m2
Qs tot = 0,8 kN/m2 + 1,08 kN/m2 + 0,36 kN/m2 + 0,07 kN/m2 + 0,5 kN/m2 + 1 kN/m2 = 3,81 kN/m2
3- CARICO ACCIDENTALE (Qa)
2,00 kN/m2 à valore tabellato da normativa, dipendente dalla destinazione d’uso dell’ambiente architettonico preso in esame, in questo caso ho scelto di immaginare il solaio come interpiano di un edificio per uffici.
4- CALCOLO IL CARICO ULTIMO
Qu = (1,3*qs + 1,5*qp + 1,5*qa)* i = (1,3 * 0,64 + 1,5 * 3,81 + 1,5 * 2)* 6 = 57,282 kN/m2
5- SCELGO LA CLASSE DI RESISTENZA
Si sceglie di realizzare il solaio con un legno lamellare GL24C (fm,k = 24 N/mm2), con una classe di servizio 2 (lunga), quindi il kmod = 0,70.
Il foglio excell si calcola poi la resistenza di progetto, definita dal prodotto della resistenza caratteristica del legno fm,k per il coefficiente di degrado nel tempo kmod diviso il coefficiente di sicurezza γm (1,45 da normativa)
6- DIMENSIONAMENTO TRAVE
Si imposta la base della trave di 20 cm e si ricava l’altezza.
Si inseriscono i dati nella tabella Excel per dimensionare la trave.
L’altezza minima della trave deve essere di 40,85 cm infatti:
Wx= Mx/fd
Per una sezione rettangolare omogenea Wx = 1/6*b*h
h = √[(6Mx)/(b*fd)] = l*α
Si prende una sezione di 20x45 cm.
7- DEFORMABILITA’: STATI LIMITE D’ESERCIZIO (SLE)
Ci troviamo nel campo elastico, quindi dovremmo verificare che il rapporto tra la luce della mensola ed il suo spostamento sia maggiore di 250 come imposto dalla normativa. Per fare ciò, bisogna calcolare il momento di inerzia dato da (b*h3)/12, bisogna ricalcolare il carico allo stato limite d’ esercizio (Qs +Qp + 0.5*Qa) * interasse (si può trascurare il peso della trave in legno) ed infine lo spostamento verticale massimo della mensola che come sappiamo è (qL4)/8EI. A questo momento verifico se il rapporto L/Vmax sia inferiore a 250 per accertarmi che la trave superi la prova a deformabilità a stato limite d’esercizio.
La trave di legno 20x45 è verificata.

Commenti recenti