Lo scopo è il dimensionamento di una mensola in tre tecnologie costruttive: acciaio, legno e calcestruzzo armato.
La mensola presa in analisi si presenta in questo schema strutturale:
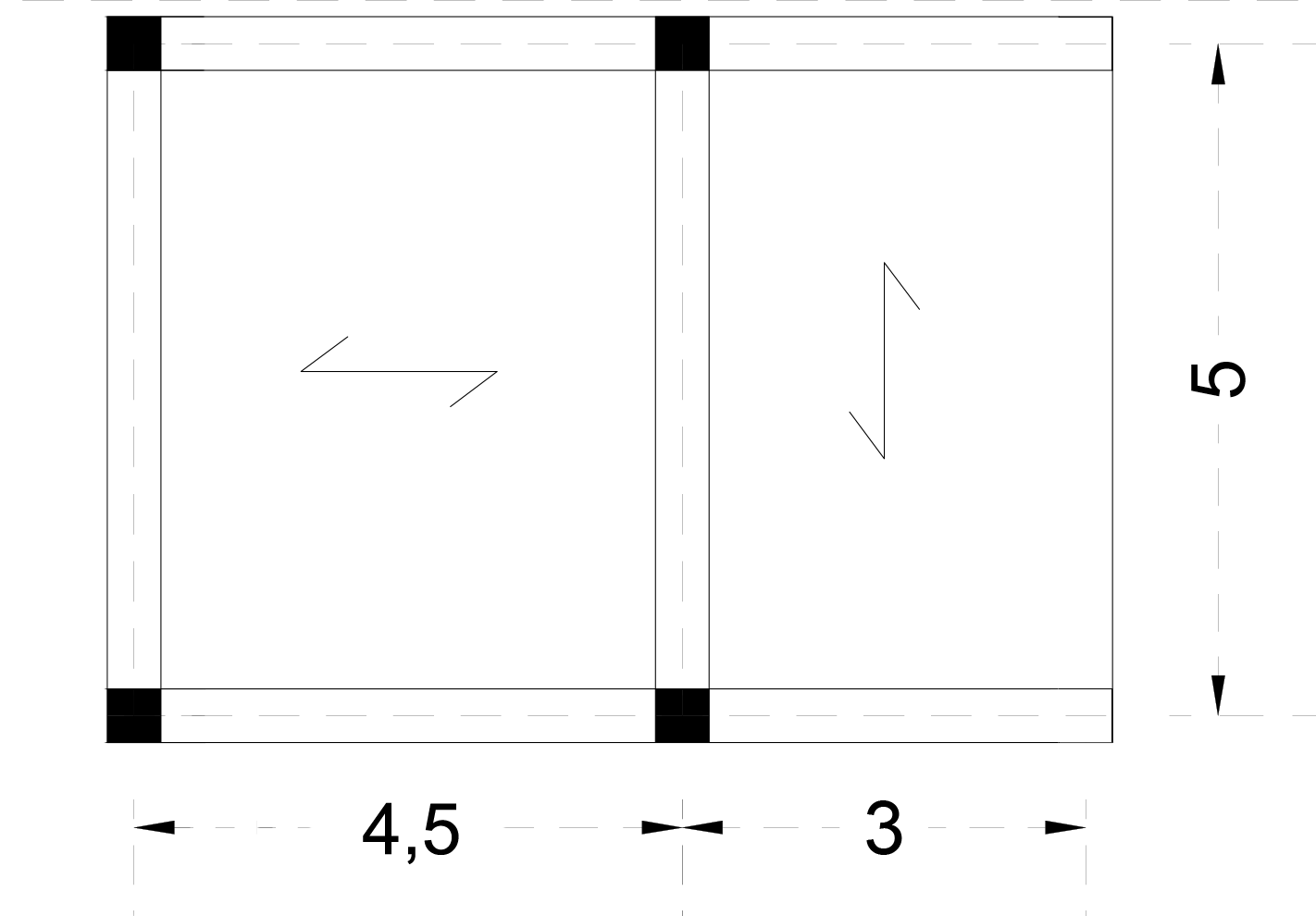 Si procede quindi con l'analisi dei carichi e il dimensionamento nei tre diversi casi.
Si procede quindi con l'analisi dei carichi e il dimensionamento nei tre diversi casi.
ANALISI E DIMENSIONAMENTO DELLA MENSOLA IN ACCIAIO CON SOLAIO IN LAMIERA GRECATA
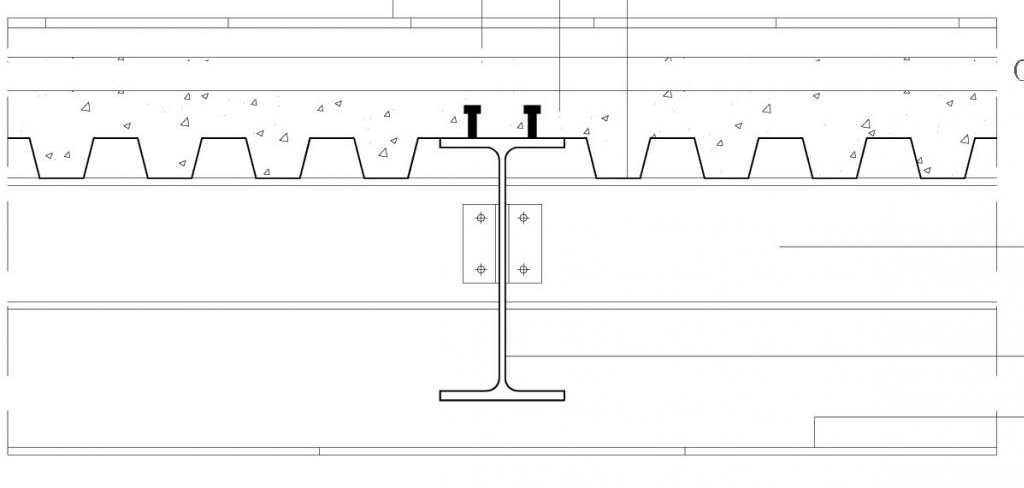
Elementi che compongono il solaio in lamiera grecata:
Getto di calcestruzzo: spessore 3,5 cm + 7 cm nella lamiera grecata; peso specifico: 25 KN/mc
Lamiera grecata: altezza 7 cm, spessore 0,088 cm; peso areale: 0,11 KN/ mq
Massetto: spessore 5 cm; peso specifico: 19 KN/mc
Pavimento: spessore 2 cm; peso specifico: 20 KN/mc
Isolante in poliuretano a bassa densità: spessore 4 cm; peso specifico: 1,8 KN/mc
Calcolo dei carichi strutturali qs
Getto di calcestruzzo : 0,035 m x 25 KN/mc = 0,875 KN/mq + [0,07 m x 25 KN/mc] x 0,5 = 0,875 KN/mq per cui in tot. =1,75 KN/mq
Lamiera grecata : 0,11 KN/mq
qs= 0,875 KN/mq + 0,11 KN/mq= 1,86 KN/mq
Calcolo dei carichi permanenti non strutturali qp
Massetto: 0,05 m x 19 KN/mc = 0,95 KN/mq
Isolante: 0,04 m x 1,8 KN/mc = 0,072 KN/mq
Pavimento: 0,02 m x 20 KN/mc = 0,4 KN/mq
Tramezzi: 1 KN/mq
Impianti: 0,5 KN/mq
qp= 0,4 KN/mq + 0,95 KN/mq + 0,072 KN/mq + 1 KN/mq + 0,5 KN/ mq = 2,92 KN/mq
Calcolo dei carichi accidentali qa
qa= 2 KN/mq da normativa per edifici residenziali
Dimensionamento della mensola con tabella Excel
Nella tabella inserisco il dato dimensionale dell'interasse e i valori dei carichi qs, qp e qa: questo mi fornirà il valore del carico qu che, insieme alla lunghezza della luce permette di calcolare il momento massimo (qxl quadro/2). La scelta del materiale (acciaio per carpenterie S275) e quindi l'inserimento del dato della sua tensione di snervamento fyk renderà possibile stabilire la tensione di progetto fyd e di conseguenza anche il modulo di resistenza a flessione Wx minimo (841,74 cm cubi). Sui profilari, scelgo una IPE 360 con un Wx di 903,6 cm cubi, un momento d'inerzia Ix di 16270 cm alla quarta ed un peso di 0,571 KN/m. Questi dati mi forniranno il carico qe che tiene in considerazione anche il peso del profilo; inserendo il modulo elastico E del materiale, la tabella finalmente calcolerà l'abbassamento massimo e il suo rapporto con la lunghezza, stabilendo (secondo la normativa dev'essere ≥ 250) che il profilo scelto è valido.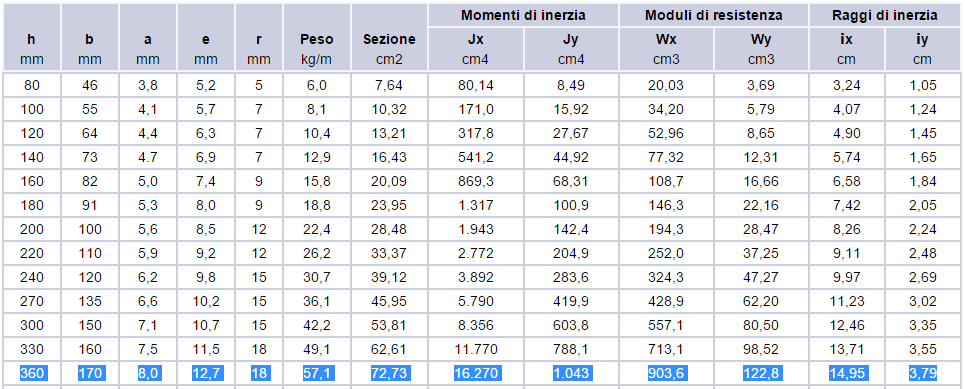

ANALISI E DIMENSIONAMENTO DELLA MENSOLA IN LEGNO CON SOLAIO IN TRAVETTI E TAVOLATO
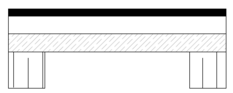
Elementi che compongono il solaio in legno:
Travetti in abete rosso: 10 x 20 cm; peso specifico: 4 KN/mc
Tavole in abete rosso: spessore 4 cm; peso specifico : KN/mc
Massetto: spessore 5 cm; peso specifico: 19 KN/mc
Pavimento: spessore 2 cm; peso specifico: 20 KN/mc
Calcolo dei carichi strutturali qs
Travetti: interasse di 40 cm (2,5 travetti per mq): (0,02 mc x 4 KN/mc)/mq x 2,5 = 0,2 KN/mq
Tavole: 0,04 m x 4 KN/mc = 0,16 KN/mq
qs= 0,2 KN/mq + 0,16 KN/mq = 0,36 KN/mq
Calcolo dei carichi permanenti non strutturali qp
Massetto: 0,05 m x 19 KN/mc = 0,95 KN/mq
Pavimento: 0,02 m x 20 KN/mc = 0,4 KN/mq
Tramezzi: 1 KN/mq
Impianti: 0,5 KN/mq
qp= 0,4 KN/mq + 0,95 KN/mq + 1 KN/mq + 0,5 KN/ mq = 2,85 KN/mq
Calcolo dei carichi accidentali qa
qa= 2 KN/mq da normativa per edifici residenziali
Dimensionamento della mensola con tabella Excel
Nella tabella inserisco il dato dimensionale dell'interasse e i valori dei carichi qs, qp e qa: questo mi fornirà il valore del carico qu che, insieme alla lunghezza della luce permette di calcolare il momento massimo (qxl quadro/2). La scelta del materiale (legno di abete rosso) e quindi l'inserimento dei dati della sua tensione di snervamento fmk, e dei coefficienti di sicurezza renderà possibile stabilire la tensione di progetto fdc e di conseguenza inserendo la misura della base della trave (30 cm da progetto) calcolare la dimensione minima dell'altezza che poi sarà ingegnerizzata (da 60,25 a 65 cm). Inserendo il modulo elastico E del materiale, la tabella finalmente calcolerà prima il momento d'inerzia e il carico dovuto al peso della trave, quindi l'abbassamento massimo e il suo rapporto con la lunghezza, stabilendo (secondo la normativa dev'essere ≥ 250) che il profilo scelto è valido.

ANALISI E DIMENSIONAMENTO DELLA MENSOLA IN CLS CON SOLAIO IN TRAVETTI E PIGNATTE
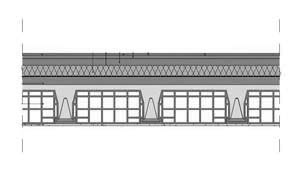
Elementi che compongono il solaio in laterocemento:
Calcestruzzo armato: spessore 4 cm + 25x10 cm dei travetti (2 per ogni metro); peso specifico: 25 KN/mc
Pignatte: 12x50x25 cm; peso areale con travetti d’interasse 60 cm: 1,05 KN/mq
Massetto: spessore 5 cm; peso specifico: 19 KN/mc
Pavimento: spessore 2 cm; peso specifico: 20 KN/mc
Isolante in poliuretano a bassa densità: spessore 4 cm; peso specifico: 1,8 KN/mc
Calcolo dei carichi strutturali qs
Calcestruzzo armato : 0,04 m x 25 KN/mc = 1 KN/mq + (0,025 mc x 25 KN/mc)/mq x 2 = 1,25 KN/mq per cui in tot. = 2,25 KN/mq
Pignatte: 1,05 KN/mq
qs=2,25 KN/mq + 1,05 KN/mq = 3,3 KN/mq
Calcolo dei carichi permanenti non strutturali qp
Massetto: 0,05 m x 19 KN/mc = 0,95 KN/mq
Isolante: 0,04 m x 1,8 KN/mc = 0,072 KN/mq
Pavimento: 0,02 m x 20 KN/mc = 0,4 KN/mq
Tramezzi: 1 KN/mq
Impianti: 0,5 KN/mq
qp= 0,4 KN/mq + 0,95 KN/mq + 0,072 KN/mq + 1 KN/mq + 0,5 KN/ mq = 2,92 KN/mq
Calcolo dei carichi accidentali qa
qa= 2 KN/mq da normativa per edifici residenziali
Dimensionamento della trave con tabella Excel
Nella tabella inserisco il dato dimensionale dell'interasse e i valori dei carichi qs, qp e qa: questo mi fornirà il valore del carico qu che, insieme alla lunghezza della luce permette di calcolare il momento massimo (qxl quadro/2). La scelta dei materiali (acciaio per armature B450c e calcestruzzo C30) e quindi l'inserimento dei dati delle loro tensioni di snervamento fyk e fck, renderà possibile stabilire le tensioni di progetto fyd e fcd e di conseguenza inserendo la misura della base della trave (25 cm da progetto) e del copriferro (5 cm da progetto) si potrà calcolare la dimensione minima dell'altezza che poi sarà ingegnerizzata (da 65,05 a 70 cm). La tabella calcolerà il peso della sezione e il carico qe che dipende da esso, e una volta inserito il valore del modulo elastico E anche il momento d'inerzia Ix e quindi l'abbassamento massimo e il suo rapporto con la lunghezza, stabilendo (secondo la normativa dev'essere ≥ 250) che il profilo scelto è valido.

Commenti recenti