ESERCITAZIONE 4_RIPARTIZIONE DELLE FORZE SISMICHE SU UN IMPALCATO IN C.A.

Si vuole calcolare la rigidezza di un impalcato costituito da sette telai di cemento armato basati sul modello teorico "shear-type", osservare la collocazione del suo centro delle rigidezze rispetto al centro di massa, e la sua capacità di rispondere alle sollecitazioni orizzontali (in particolar modo, quelle sismiche). L'impalcato è il seguente:

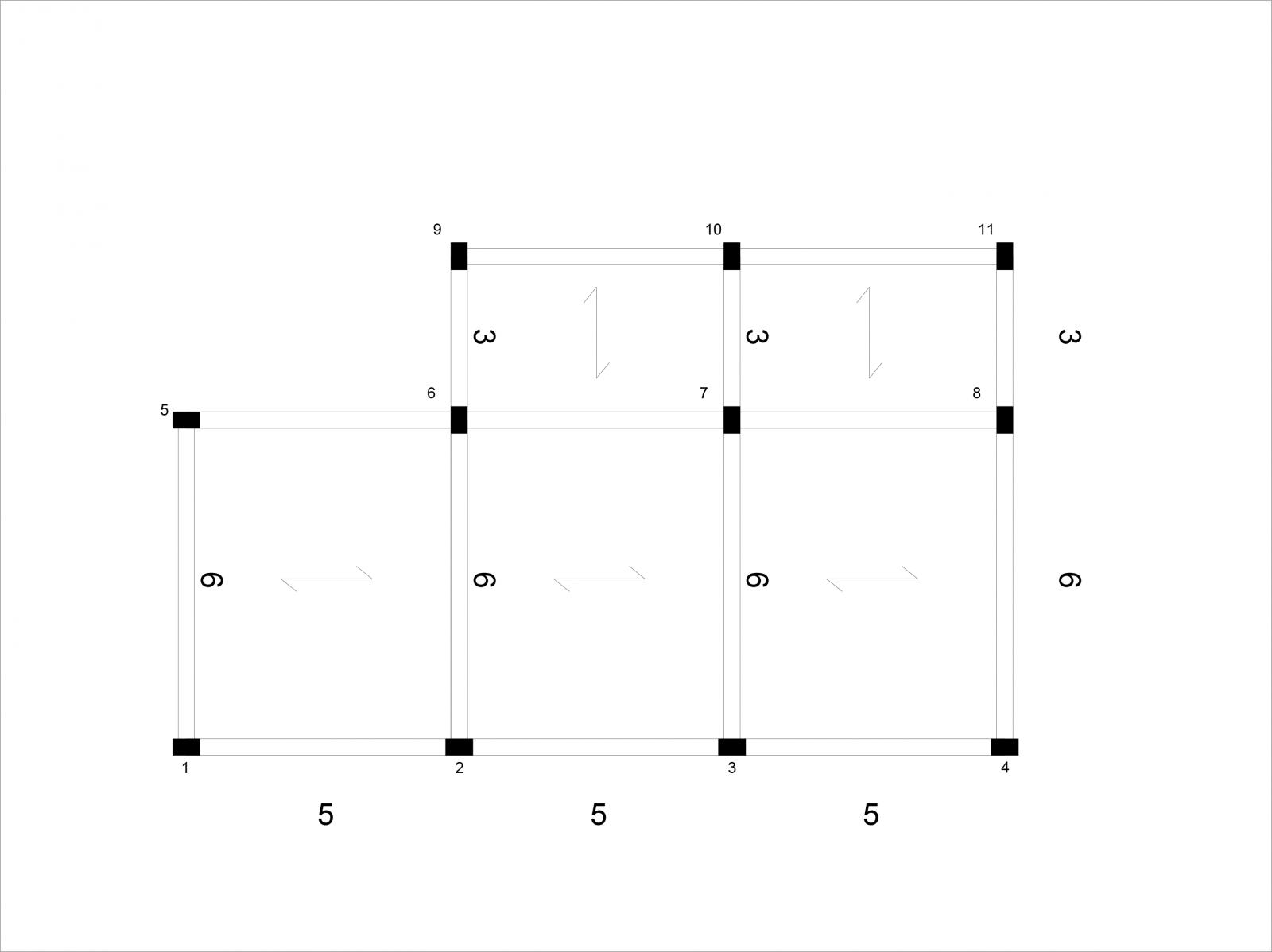I pilastri sono tutti di sezione rettangolare 30x50 cm, alcuni disposti lungo x, altri lungo y, come si piò osservare dalla pianta, e la loro altezza è di 300 cm.

Nel primo step della tabella Excel, vengono richiesti i dati riguardanti la geometria e i materiali dei vari telai: l'altezza h, il modulo plastico E (da materiale, 21000 N/mmq) e i momenti d'inerzia I (per la sezione rettangolare bh³/12, quindi 312500 cm⁴ quello maggiore, 112500 cm⁴ quello minore).

La tabella è quindi in grado di  calcolare la rigidezza traslante di ogni telaio , che si ottiene dalla formula: 

Questo perché si assume il modello "shear-type", nel quale ogni pilastro ha una rigidezza pari a 12EI/h³.

Ogni telaio è in grado di opporsi a sforzi orizzontali paralleli al suo sviluppo (possiamo quindi rappresentare ogni telaio con una molla che ostacola gli spostamenti):

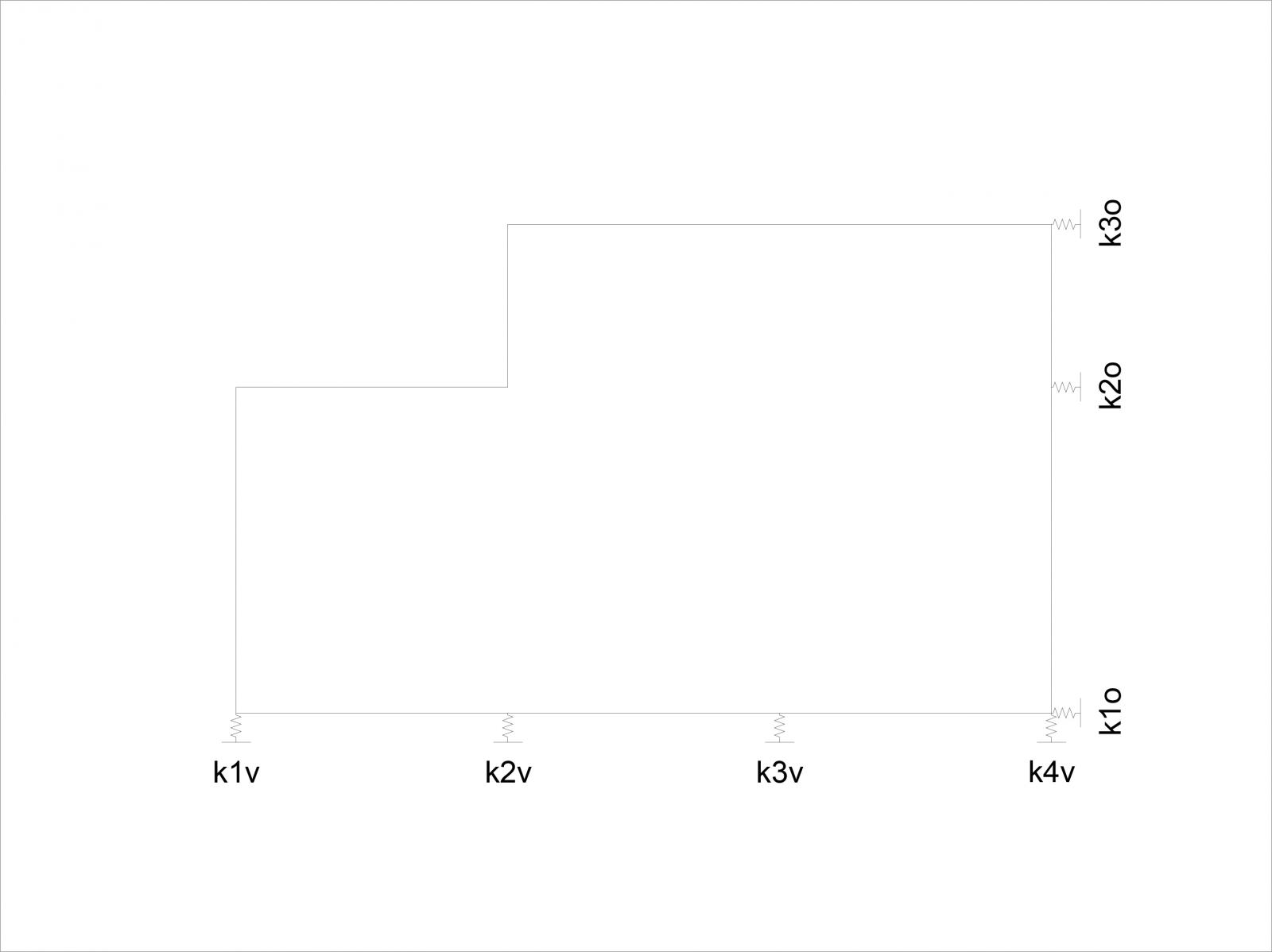
E' ora necessario calcolare le coordinate X e Y del centro di massa G, che si calcolano tenendo conto dei due centri G1 e G2 dei due rettangoli (si decide di far coincidere il centro di massa con quello d'area), ed inserendoli nella formula per il centro di un sistema di vettori paralleli:

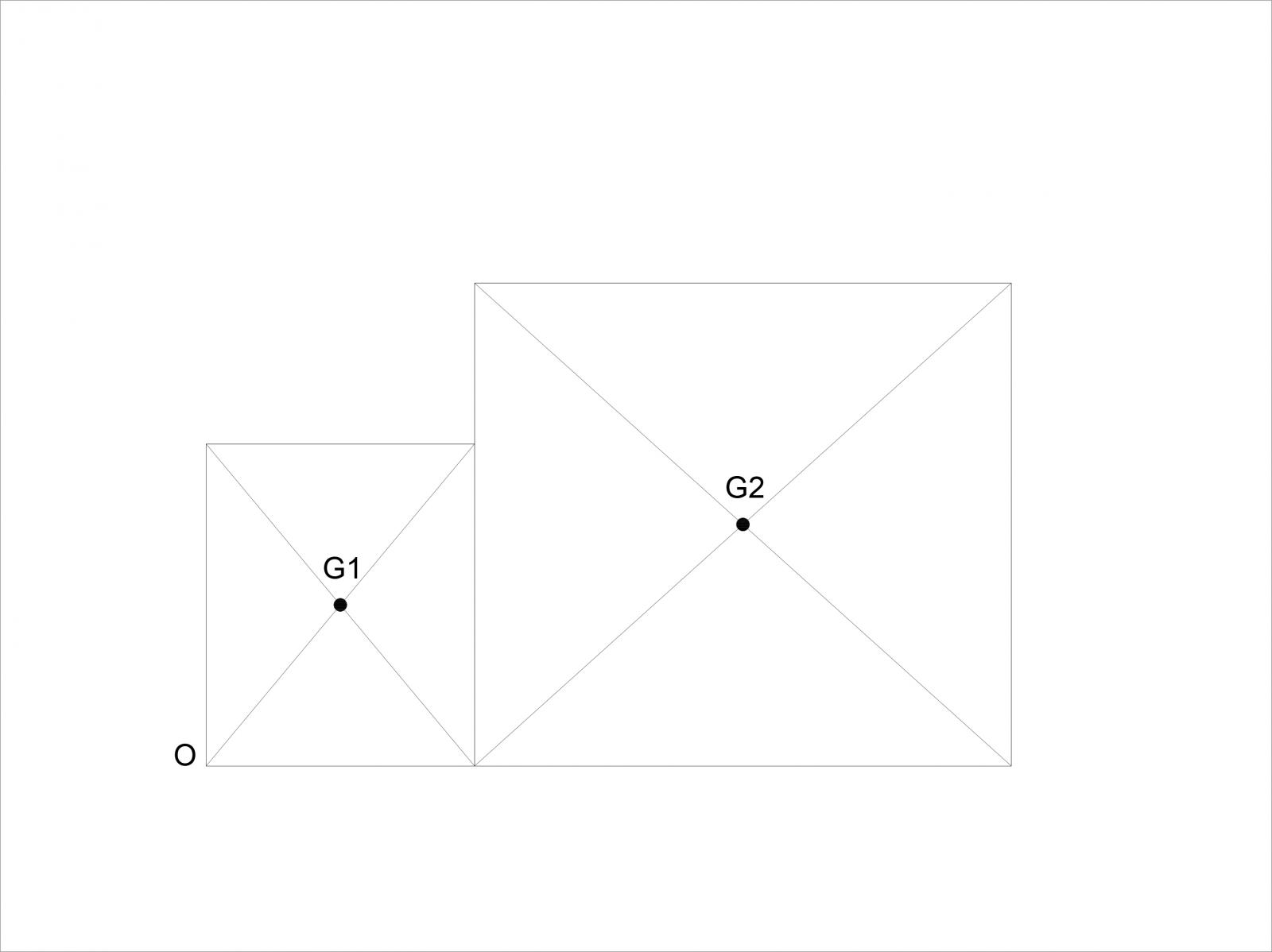
Il centro di massa risulta quindi di coordinate (8,13 m ; 4,13 m)

Dopo aver trovato G, serve trovare anche il centro delle rigidezze C, con la stessa formula del centro del sistema di vettori paralleli, i cui dati vengono raccolti nella tabella dello step 2 di cui sopra:

Il centro delle rigidezze C risulta avere coordinate (9,08 m; 2,94 m). In seguito viene mostrata la reciproca posizione di G e C nell'impalcato:

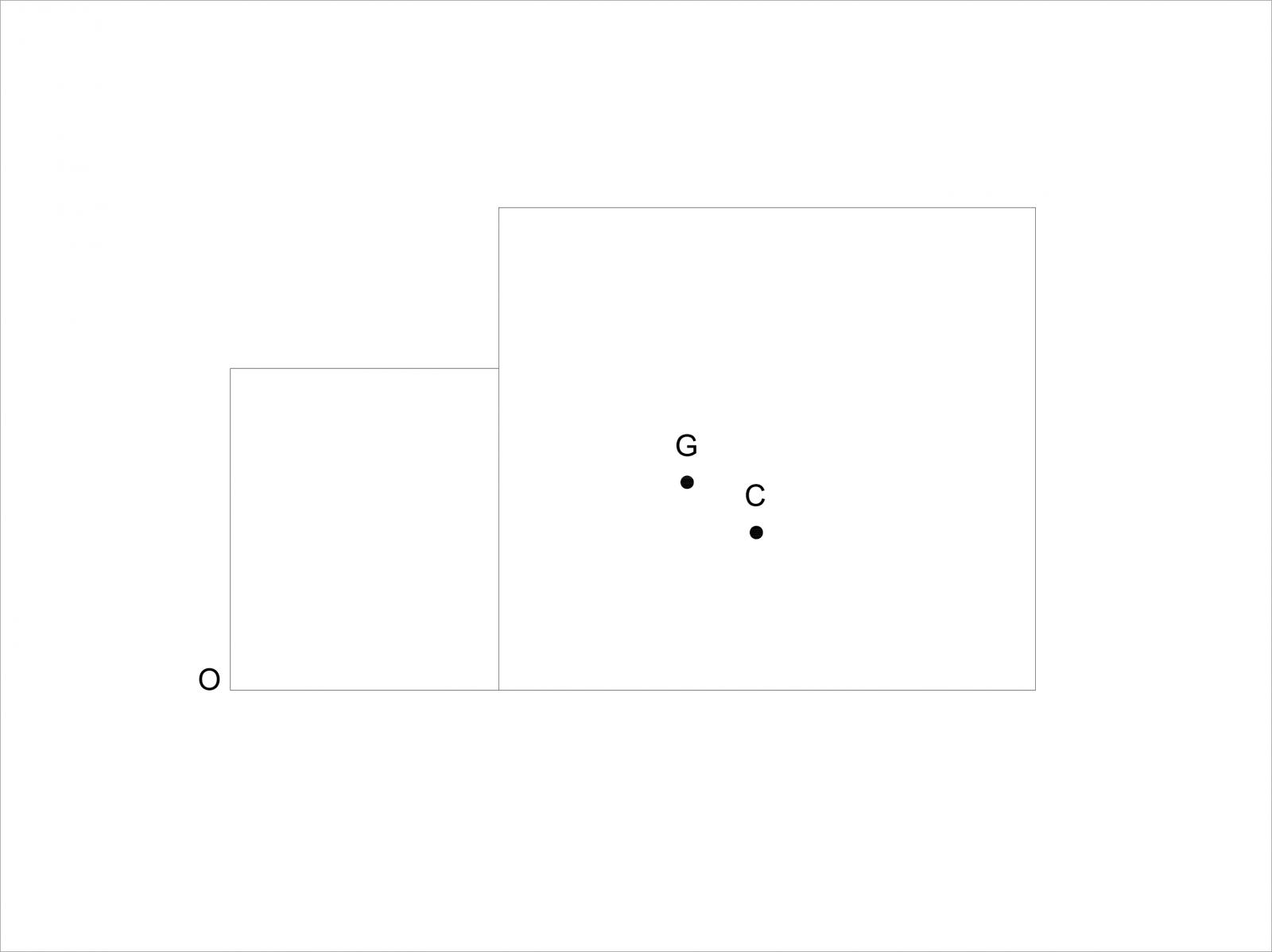
Una buona progettazione impone che i due centri non abbiano una distanza troppo elevata, onde limitare (o addirittura, annullare) la rotazione rigida dell'impalcato, e di conseguenza momenti torcenti sui pilastri, sottoponendo la struttura a sola traslazione pura. In questo caso la distanza è accettabile, anche se l'impalcato tende comunque a ruotare: è necessario allora calcolare la sua rigidezza torsionale come mostrato nella tabella dello step 4 di cui sopra.

Il foglio Excel calcola quindi prima le distanze dei controventi dal centro delle rigidezze, in modo da poter applicare la formula seguente:

La rigidezza torsionale totale risulta quindi 7877467,28 KNm.

Lo step 5 riguarda il calcolo dell'entità del carico sismico dell'impalcato, per il quale è necessario conoscere i carichi strutturali qs, i carichi permanenti non strutturali qp ed i carichi accidentali qa: si considera un solaio in laterocemento (vedere esercitazioni 2 e 3 per dettagli) ad uso residenziale, ovvero:

qs=1,86 KN/mq, qp=1,91 KN/mq, qa=2 KN/mq.

Essi devono essere moltiplicati per l'area dell'edificio in modo da ottenere  i carichi totali G = 452,4 KN e Q = 240 KN, a loro volta sommati e moltiplicati per il coefficiente di contemporaneità 0,8 per avere il valore del peso sismico W = 644,4 KN; infine è necessario moltiplicare per il coefficiente d'intensità sismica c, che dipende dall'area geografica e dalla sua sismicità (in questo caso vale 0,1) fino ad ottenere lo sforzo sismico orizzontale F =64,44 KN.

Gli step 6 e 7 calcolano i valori degli spostamenti orizzontali e verticali e della rotazione dell'impalcato applicando la forza F sul centro di massa G, rispettivamente lungo l'asse X e lungo l'asse Y, con le formule qui riportate:

Il momento torcente M che appare nella formula ha come forza la forza sismica F e come braccio la distanza tra centro di massa e centro delle rigidezze, e vale quindi -61,34 KNm.

La tabella quindi calcola la forza sui singoli controventi (sempre una volta per Fx e una per Fy) e per fare ciò utilizza le seguenti formule nel caso della forza lungo X: 

rispettivamente per i controventi orizzontali e quelli verticali;  Lo stesso principio si applica con la forza lungo Y: