blog di tommaso.spagnuolo

Ipotizzata la struttura in figura, la trave che mi accingo a dimensionare è quella maggiormente sollecitata, ossia quella evidenziata d’arancione, in quanto interessata dalla maggiore area di influenza - 15 m² (dove 3 m = luce, 5 m = interasse).

 

TRAVE IN LEGNO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 0,438 kN/m²

      q_p = 2,69 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel (scaricabile dalla sezione Download del Portale di Meccanica), ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (0.438 kN/m²), di q_p (2.69 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco i seguenti valori:

• resistenza a flessione caratteristica f_m,k = 24 MPa (dipendente dal tipo di legno, ovvero lamellare GL 24h)
• coefficiente della durata del carico k_mod = 0,8 (fornito dalla normativa)
• coefficiente parziale di sicurezza del materiale γ_m = 1,45 (legno lamellare)

e ottengo la tensione ammissibile f_d [N/mm²], secondo la formula seguente:

      f_d = f_m,k x k_mod / γ_m

Ipotizzo il valore della base b (40 cm) e ricavo l’altezza minima h_min che la trave deve avere, secondo la seguente formula:

      h_min = (interasse x M_max x 1000 / b x f_d) ^ 0,5

Assegno quindi alla sezione una h = 60 cm.

Definisco poi il valore del modulo elastico E = 8000 N/mm², e ottengo il momento d’inerzia I_x, i carichi incidenti q_e, l’abbassamento massimo v_max  e il rapporto tra la luce e l’abbassamento massimo della trave l/v_max, rispettivamente secondo le seguenti formule

      I_x = b x h³ / 12

      q_e = (q_s + q_p + 0.5 x q_a) x i

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250, trascurando il peso proprio della trave a causa della sua leggerezza:

Essendo l/v_max (606.49) > 250 la sezione 40 x 60 cm è verificata.

 

TRAVE IN ACCIAIO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 2,01 kN/m²

      q_p = 2,84 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel, ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2.01 kN/m²), di q_p (2.84 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco il seguente valore:

• tensione di snervamento f_y,k = 275 MPa (dipendente dal tipo di acciaio, ovvero Fe 430/ S275)

e ottengo il modulo di resistenza elastico minimo W_x,min [cm³], secondo la formula seguente:

      W_x,min = M_max / f_d x 1000

Quindi, sul sagomario, scelgo il profilo IPE 450 con W_x = 1500 cm³, I_x = 33740 cm⁴ e peso = 77.6 kg/m = 0.776 kN/m e ottengo q_e, secondo la seguente formula:

      q_e = (q_s + q_p + 0.5 x q_a) x i + p_trave

Infine definisco il valore del modulo elastico E = 210000 N/mm², e il foglio di calcolo mi fornisce il valore dell’abbassamento massimo v_max e il suo rapporto con la luce l/v_max, rispettivamente secondo le formule seguenti:

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250.

Essendo l/v_max (559.446) > 250 il profilo IPE 450 è verificato.

 

TRAVE IN CALCESTRUZZO ARMATO

1| Analisi dei carichi

I carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare sono gli stessi dell'Esercitazione 2.

      q_s = 2,368 kN/m²

      q_p = 2,654 kN/m²

      q_a = 5,00 kN/m²

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel, ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2.368 kN/m²), di q_p (2.654 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (3 m) e ottengo il momento massimo della stessa – intesa come una mensola, secondo la formula M_max = ql²/2

Poi fornisco il seguente valore:

• tensione di snervamento dell’acciaio f_yk = 450 MPa (dipendente dal tipo di acciaio, ovvero B450C)

e ottengo la tensione di progetto dell’acciaio f_yd [MPa], secondo la formula seguente:

      f_yd = f_yk / γ_s, dove γ_s = 1,15

Mentre, per la tensione di progetto del calcestruzzo (cls) f_cd, fornisco la resistenza caratteristica a compressione R_ck (40 N/mm²) e il foglio Excel me lo calcola, secondo la formula seguente:

      f_cd = 0,85 x R_ck / γ_c, dove γ_c = coefficiente parziale di sicurezza = 1,5 

oltre a calcolarmi β (0.46) e r (2.26).

Ipotizzo il valore della base b (40 cm) e ricavo prima l’altezza utile minima h_u,min, secondo la seguente formula:

      h_u,min = r x (M_max x 1000 / (f_cd x b)) ^ 0,5

e poi l’altezza minima H_min, secondo la formula seguente:

      H_min = h_u,min + Δ, dove Δ = copriferro = 5 cm

Assegno quindi alla sezione una H = 50 cm, e il foglio di calcolo mi fornisce q_e secondo la formula seguente:

      q_e = (q_s + q_p + 0.5 x q_a) x i + p_trave

Infine definisco il valore del modulo elastico E = 21000 N/mm² e ottengo il momento d’inerzia I_x, l’abbassamento massimo v_max e il rapporto tra la luce e l’abbassamento massimo l/v_max, rispettivamente secondo le seguenti formule:

      I_x = b x h³ / 12

      v_max = q_e x 10 x (l x 100)⁴ / (8 x E x 100 x I_x)

3| Verifica

A questo punto, come fatto per la trave in legno e in acciaio, verifico che il rapporto tra la luce e l’abbassamento massimo della trave sia maggiore o uguale a 250, ossia l/v_max ≥ 250.

Essendo l/v_max (1594.73) > 250 la sezione 40 x 50 cm è verificata.

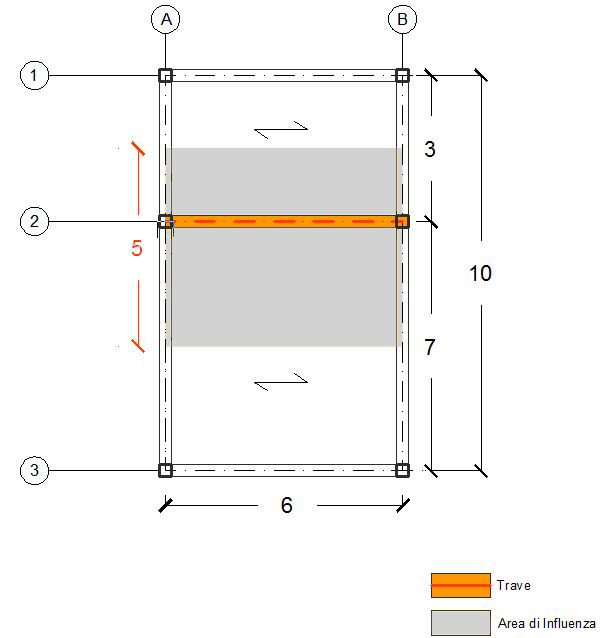
Ipotizzata la struttura in figura, la trave che mi accingo a dimensionare - in legno, acciaio e calcestruzzo armato - è quella maggiormente sollecitata, ovvero interessata dalla maggiore area di influenza - 30 m², dove 5 m = interasse e 6 m = luce.

 

TRAVE IN LEGNO

1| Analisi dei carichi

Come prima cosa, calcolo i carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare.

*Carichi strutturali

Travetto con sezione 12x22 cm e peso specifico 6 kN/m³

      q₁= (0,12 x 0,22 x 1) m³/m² x 6 kN/m³ = 0,158 kN/m²

Tavolato con spessore 4 cm e peso specifico 7 kN/m³

      q₂= (0,04 x 1 x 1) m³/m² x 7 kN/m³ = 0,28 kN/m²

quindi calcolo il carico strutturale q_s trascurando il peso proprio della trave:

      q_s = q₁ + q₂ = 0,158 kN/m² + 0,28 kN/m² = 0,438 kN/m²

*Carichi permanenti

Caldana con spessore 4 cm e peso specifico 0,28 kN/m²

      q₁ = 0,28 kN/m²

Isolante con spessore 3,5 cm e peso specifico 30 Kg/m³ =  0,3 kN/m³

      q₂ = (0,035 x 1 x 1) m³/m² x 0,3 kN/m³ = 0,0105 kN/m²

Sottofondo con spessore 3 cm e peso specifico 0,54 kN/m²

      q₃ = 0,54 kN/m²

Pavimento in cotto con spessore 2 cm e peso specifico pari a 18 kN/m³

      q₄ = (0,02 x 1 x 1) m³/m² x 18 kN/m³ = 0,36 kN/m²

quindi calcolo il carico permanente q_p aggiungendo l’incidenza degli impianti e dei tramezzi:

      q_p = q₁ + q₂ + q₃ + q₄ = 0,28 kN/m² + 0,0105 kN/m² + 0,54 kN/m² + 0,36 kN/m² = 1,19 kN/m² + 0,5 kN/m² +

      + 1 kN/m² = 2,69 kN/m²

*Carichi accidentali 

Ipotizzo che l’edificio di cui la trave fa parte sia adibito a uso commerciale, in particolare a libreria:

      q_a = 5,00 kN/m² (fornito dalla normativa – NTC 2008)

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel (scaricabile dalla sezione Download del Portale di Meccanica), ricavo il carico totale q_u. Quindi inserisco i valori dell’interasse (5 m), di q_s (0.438 kN/m²), di q_p (2.69 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale_, secondo la formula seguente:

      q_u = ((q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)) x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (6 m) e ottengo il momento massimo M_max della stessa – intesa come semplicemente appoggiata, secondo la seguente formula: 

      M_max = ql² / 8

Poi fornisco i seguenti valori:

• resistenza a flessione caratteristica f_m,k = 24 MPa (dipendente dal tipo di legno, ossia lamellare GL 24h)
• coefficiente della durata del carico k_mod = 0,8 (fornito dalla normativa - NTC 2008)
• coefficiente parziale di sicurezza del materiale γ_m = 1,45 (dipendente dal tipo di legno, ossia lamellare)

e ottengo la tensione ammissibile f_d [N/mm²], secondo la formula seguente:

      f_d = f_m,k x k_mod / γ_m

Infine, ipotizzo il valore della base b (40 cm) e ricavo l’altezza minima h_min che la trave deve avere, secondo la seguente formula:

      h_min = (interasse x M_max x 1000 / b x f_d) ^ 0,5

Assegno quindi alla sezione una h = 60 cm, che come si può notare non è il valore immediatamente maggiore di h_min (per esempio 55 cm). Questo per tenere in conto il fatto che ho, per il momento, trascurato il peso proprio della trave.

3| Verifica

A questo punto, scelto il valore di h, verifico la trave considerando il suo peso proprio p.p. [kN/m]:

      p.p. = (0,40 x 0,60 x 1) m³/m x 6 kN/m³ = 1,44 kN/m

che, moltiplicato per 1,3, va a sommarsi ai carichi strutturali q_s in parte già calcolati,:

      q_s = q₁ + q₂ + p.p. x 1,3 = (0,438 + 1,44 x 1,3) kN/m² = 2,31 kN/m²

Quindi, inserisco il nuovo valore di q_s e il foglio di calcolo mi fornisce la nuova h_min, che deve essere minore dell’altezza scelta h affinché la trave sopporti – senza rompersi – il suo carico.

Essendo h_min (59,74 cm) < h (60 cm) la sezione 40 x 60 cm è verificata.

 

TRAVE IN ACCIAIO

1| Analisi dei carichi

Per prima cosa, calcolo i carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare.

*Carichi strutturali

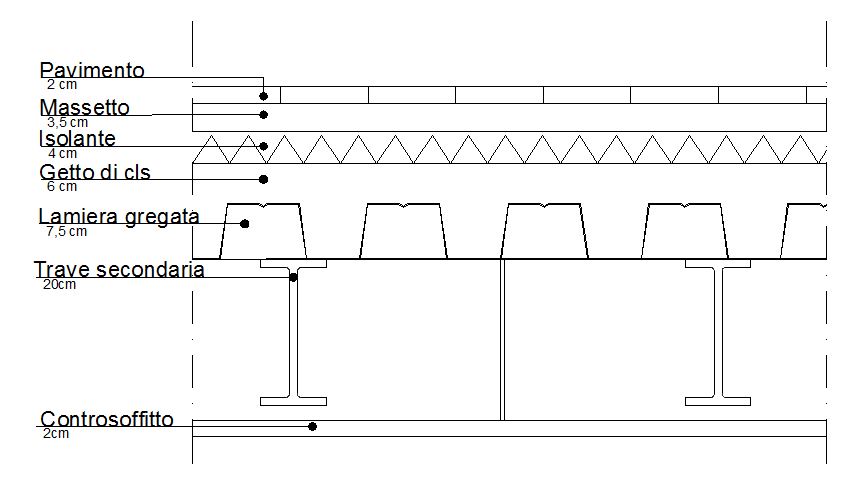
Trave secondaria - IPE 200 - con area della sezione 0,00285 m² e peso specifico 78,5 kN/m³

      q₁ = (0,00285 m² x 1 m) x  78,5 kN/m³ = 0,224 kN/m²

Lamiera gregata con altezza 7,5 cm e peso specifico 11 Kg/m² = 0,11 kN/m²

      q₂ = 0,11 kN/m²

Getto di cls con volume 0,07 m³ e peso specifico 24 kN/m³

      q₃ = 0,07 m³/m² x  24 kN/m³ = 1,68 kN/m²

quindi calcolo il carico strutturale q_s trascurando il peso proprio della trave:

      qs = q₁ + q₂  +q₃ = 0,224 kN/m² + 0,11 kN/m² +  1,68 kN/m² = 2,01 kN/m²

*Carichi permanenti

Controsoffitto con peso specifico 0,3 kN/m²

      q₁ = 0,3 kN/m²

Isolante con altezza 4 cm e peso specifico 35 Kg/m³ =  0,35 kN/m³

      q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto con spessore 3,5 cm e peso specifico 18 kN/m³

      q₃ = (0,035 x 1 x 1) m³/m² x 18kN/m³ = 0,63 kN/m²

Pavimento in ceramica con peso specifico 0,4 kN/m²

      q₄ = 0,4 kN/m²

quindi calcolo il carico permanente q_p aggiungendo l’incidenza degli impianti e dei tramezzi:

      qp = q₁ + q₂ + q₃ + q₄ = 0,3 kN/m² + 0,014 kN/m² + 0,63 kN/m² + 0,4 kN/m² = 1,34 kN/m² + 0,5 kN/m² + 

      + 1 kN/m² = 2,84 kN/m²

*Carichi accidentali

Ipotizzo che l’edificio di cui la trave fa parte sia adibito a uso commerciale, in particolare a libreria:

      q_a = 5,00 kN/m² (fornito dalla normativa – NTC 2008)

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel (scaricabile dalla sezione Download del Portale di Meccanica), ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2,01 kN/m²), di q_p (2,84 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = ((q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)) x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (6 m) e ottengo il momento massimo M_max della stessa – intesa come semplicemente appoggiata, secondo la seguente formula: 

      M_max = ql² / 8

Poi fornisco il seguente valore:

• tensione di snervamento f_y,k = 275 MPa (dipendente dal tipo di acciaio, ossia Fe 430/S275)

e ottengo il modulo di resistenza elastico minimo W_x,min [cm³], secondo la formula seguente:

      W_x,min = M_max / f_d x 1000

Quindi, sul sagomario, scelgo il profilo IPE 450 con W_x = 1500 cm³.

3| Verifica

A questo punto, scelto il profilo, lo verifico considerando il suo peso proprio p.p. [kN/m]:

      p.p. = (0,00988 x 1) m³/m x 78,5 kN/m³ = 0,77 kN/m

che, moltiplicato per 1,3, va a sommarsi ai carichi strutturali q_s in parte già calcolati:

      q_s = q₁ + q₂ + q₃ + p.p. x 1,3 = (2,01 + 0,77 x 1,3) kN/m² = 3.01 kN/m²

Quindi, inserisco il nuovo valore di q_s e il foglio di calcolo mi fornisce il nuovo W_x,min, che deve essere minore del modulo di resistenza elastico associato al profilo scelto W_x, affinché la trave sopporti – senza rompersi – il suo carico.

Essendo W_x,min (1421,24 cm³) < W_x (1500 cm³) il profilo IPE 450 è verificato.

 

TRAVE IN CALCESTRUZZO ARMATO

1| Analisi dei carichi

Come fatto per il legno e per l'acciaio, calcolo innanzitutto i carichi - strutturali, permanenti e accidentali - che la trave dovrà sopportare.

*Carichi strutturali

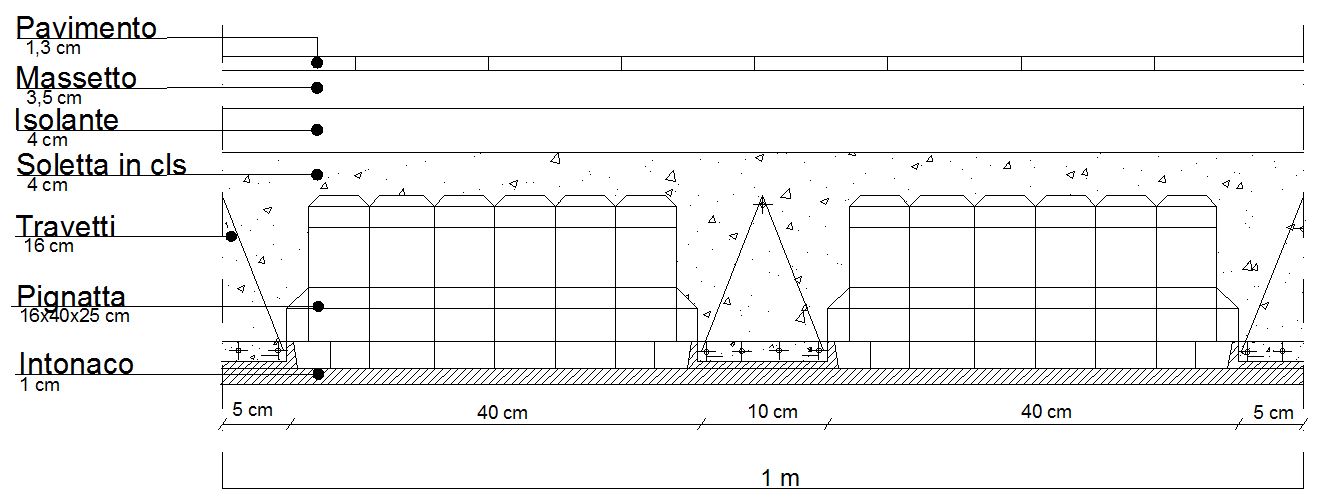
8 Pignatte con peso specifico ognuna di 8 Kg

      q₁ = 8 x 8 Kg/m² = 64 Kg/m² = 0,64 kN/m²

Soletta in cls con altezza 4 cm e peso specifico 24 kN/m³

      q₂ = (0,04 x 1 x 1) m³/m² x 24 kN/m³ = 0,96 kN/m²

Travetti con altezza 16 cm e peso specifico 24 kN/m³

      q₃ = 2 x(0,16 x 0,1 x1)m³/m² x  24 kN/m³ = 0,768 kN/m²

quindi calcolo il carico strutturale q_s trascurando il peso proprio della trave:

      q_s = q₁ + q₂  +q₃ = 0,64 kN/m² + 0,96 kN/m² +  0,768 kN/m² = 2,368 kN/m²

*Carichi permanenti

Intonaco con spessore 1 cm e peso specifico 16 kN/m³

      q₁ = (0,01 x 1 x 1)m³/m² x 16 kN/m³ = 0,16 kN/m²

Isolante con altezza 4 cm e peso specifico 35 Kg/m³ = 0,35 kN/m³

      q₂ = (0,04 x 1 x 1) m³/m² x 0,35 kN/m³ = 0,014  kN/m²

Massetto con spessore 3,5 cm e peso specifico 2000 Kg/m³ =  20 kN/m³

      q₃ = (0,035 x 1 x 1) m³/m² x 20 kN/m³ = 0,7 kN/m²

Pavimento in cotto con peso specifico 28 Kg/m²

      q₄ = 0,28 kN/m²

quindi calcolo il carico permanente q_p aggiungendo l’incidenza degli impianti e dei tramezzi:

      q_p = q₁ + q₂ + q₃ + q₄ = 0,16 kN/m² + 0,014 kN/m² + 0,7 kN/m² + 0,28 kN/m² = 1,154 kN/m² + 0,5 kN/m² +

      + 1 kN/m² = 2,654 kN/m²

*Carichi accidentali

Ipotizzo che l’edificio di cui la trave fa parte sia adibito a uso commerciale, in particolare a libreria:

      q_a = 5,00 kN/m² (fornito dalla normativa – NTC 2008)

**Carico totale

A questo punto, tramite il foglio di calcolo – Excel (scaricabile dalla sezione Download del Portale di Meccanica), ricavo il carico totale. Quindi inserisco i valori dell’interasse (5 m), di q_s (2,368 kN/m²), di q_p (2,654 kN/m²) e di q_a (5 kN/m²) e il foglio di calcolo mi fornisce il valore del carico totale q_u, secondo la formula seguente:

      q_u = [(q_s x 1,3) + (q_p x 1,3) + (q_a x 1,5)] x interasse

2| Progetto

Come seconda cosa, servendomi sempre del foglio di calcolo – Excel, inserisco la luce della trave (6 m) e ottengo il momento massimo M_max della stessa – intesa come semplicemente appoggiata, secondo la seguente formula: 

      M_max = ql² / 8

Poi fornisco il seguente valore:

• tensione di snervamento dell’acciaio f_yk = 450 MPa (dipendente dal tipo di acciaio, ossia B450C)

e ottengo la tensione di progetto dell’acciaio f_yd [MPa], secondo la formula seguente:

      f_yd = f_yk / γ_s, dove γ_s = coefficiente parziale di sicurezza = 1,15

Mentre, per la tensione di progetto del calcestruzzo f_cd, fornisco la resistenza caratteristica a compressione R_ck (40 N/mm²) e il foglio Excel me lo calcola, secondo la formula seguente:

      f_cd = 0,85 x R_ck / γ_c, dove γ_c = coefficiente parziale di sicurezza = 1,5

oltre a calcolarmi α e r.

Infine, ipotizzo il valore della base b (40 cm) e ricavo prima l’altezza utile minima h_u,min, secondo la seguente formula:

      h_u,min = r x (M_max x 1000 / (f_cd x b)) ^ 0,5

e poi l’altezza minima H_min, secondo la formula seguente:

      H_min = h_u,min + Δ, dove Δ = copriferro = 5 cm

Assegno quindi alla sezione una H = 65 cm, che come si può notare non è il valore immediatamente maggiore di H_min (per esempio 50 cm). Questo per tenere in conto il fatto che ho, per il momento, trascurato il peso proprio della trave.

3| Verifica

A questo punto, definita la sezione, la verifico considerando il peso proprio della trave p.p. [kN/m]:

      p.p. = (0,40 x 0,65 x 1) m³/m² x 25 kN/m³ = 6,5 kN/m²

che, moltiplicato per 1,3, va a sommarsi ai carichi strutturali q_s già in parte calcolati:

      q_s = q₁ + q₂ + q₃ + p.p. x 1,3 = (2,368 + 6,5 x 1,3) kN/m² = 10,818 kN/m²

Quindi, inserisco il nuovo valore di q_s e il foglio di calcolo mi fornisce la nuova H_min, che deve essere minore dell’altezza scelta H, affinché la trave sopporti – senza rompersi – il suo carico.

Essendo H_min (61,21 cm) < H (65 cm) la sezione 40 x 65 cm è verificata.

Softwares utilizzati: SAP2000 17, Excel 2013.

 

1| Griglia su cui disegnare la struttura

File > New Model (KN, m, C; Grid Only) > Quick Grid Lines (Number of Grid Lines: X=4, Y= 7, Z= 2; Grid Spacing (X= 3, Y= 3, Z= 3); First Grid Line Location (X= Y= Z= 0) > OK

2| Disegno di un modulo della struttura

Frame > disegno la base quadrata superiore e la controvento con un'asta >> Draw Special Joint > fisso il punto in A1 > lo seleziono col tasto destro del mouse e mi si apre la finestra Object Model_Point Information (Location: X= 1.5, Y= 1.5) > OK >> Frame > completo il modulo

3| Reiterazione del modulo fino ad ottenere la struttura complessiva

Set Select Mode > seleziono il modulo tranne l'asta tra i punti A1 e B1 > ctrl+c > ctrl+v > Paste Coordinates (Delta X= 0, Delta Y= 3, Delta Z= 0) > OK >> seleziono i due moduli tranne l'asta tra i punti A1 e B1 > ctrl+c > ctrl+v > Paste Coordinates (Delta X= 0, Delta Y= 6, Delta Z= 0) > OK >> seleziono solo gli ultimi due moduli tranne l'asta tra i punti A3 e B3 > ctrl+c > ctrl+v > Paste Coordinates (Delta X= 0, Delta Y= 6, Delta Z= 0) > OK >> seleziono tutti e sei i moduli tranne tutte le aste lungo A > ctrl+c > ctrl+v > Paste Coordinates (Delta X= 3, Delta Y= 0, Delta Z= 0) > OK >> seleziono i sei i moduli compresi fra A e B tranne tutte le aste lungo A > ctrl+c > ctrl+v > Paste Coordinates (Delta X= 6, Delta Y= 0, Delta Z= 0) > OK >> Frame > collego tutti i vertici inferiori fra di loro

4| Vincoli esterni (cerniere)

Set Select Mode > seleziono i quattro vertici inferiori-perimetrali della struttura > Assign > Joint > Restraints > Joint Restraints (Fast Restraints: seleziono il simbolo della cerniera esterna) > OK

 5| Vincoli interni (cerniere)

Set Select Mode > seleziono l'intera struttura > Assign > Frame > Releases/Partial Fixity... > Assign Frame Releases > spunto Moment 22 e Moment 33 sia in Start sia in End > OK

6| Materiale e sezione delle aste

Set Select Mode > seleziono l'intera struttura > Assign > Frame > Frame Section > Frame Properties (Add New Property... > Add Frame Section Property (Steel > Pipe > Pipe Section (in Section Name scrivo Pipe) > OK > OK

7| Carico (concentrato sui nodi superiori) 

Define > Load Patterns... > Define Load Patterns (in Load Pattern Name scrivo F e in Self Weight Multipler scrivo 0 > Add New Load Pattern) > OK >> seleziono tutti i nodi superiori della struttura > Assign > Joint Loads > Forces... > Joint Forces (Load Pattern Name: F, Loads: Force Global Z: -50) > OK

8| Analisi

Run Analysis > Set Load Cases to Run (seleziono Dead e Modal, ossia i carichi da trascurare nell'analisi, e clicco su Run/Do Not Run Case) > Run Now

Dall'analisi osservo che la struttura è soggetta soltanto a sforzo normale N, di trazione (blu) e di compressione (rosso).

9| Tabelle analisi 

Display > Show Tables > Choose Tables for Display: spunto su ANALYSIS RESULTS > OK >> Assembled Joint Masses: seleziono Element Forces - Frames, File > Export Current Table To Excel > cancello tutte le colonne dopo quella E (perché non necessarie) > inserisco una nuova colonna per la luce delle aste > individuo in rosso le aste diagonali che valgono 3√2 e in arancione le aste diagonali spaziali che valgono 3√(3/2) > cancello i doppioni delle aste con Rimuovi duplicati secondo Frame > ordino la tabella secondo lo sforzo normale P dal più grande al più piccolo (dai positivi-trazione ai negativi-compressione)

10| Foglio di calcolo Excel per il dimensionamento delle aste

Apro il Foglio di calcolo_pilastri scaricabile dal Portale di Meccanica nella sezione Download > elimino il contenuto delle colonne che precedono quella relativa allo sforzo normale N > copio dalla Tabella-Sap tutti i valori dello sforzo normale e delle luci delle aste e gli incollo nelle relative colonne del Foglio di calcolo > definisco f_yk= 275 MPa e γ_m= 1.05 e il foglio di calcolo mi fornisce l’A_min > per ogni asta tesa, scelgo sul sagomario il profilo con l’A immediatamente superiore ad A_min; per ogni asta compressa, invece, definisco E= 210'000 MPa e β= 1 e il foglio di calcolo mi fornisce λ*, ρ_min e I_min, quindi sul sagomario scelgo il profilo che abbia ρ > ρ_min, I > I_min e A > A_min

11| Raggruppamento dei profili

Seleziono la colonna dei profili adottati e faccio ordina i dati dal valore più basso al più alto, in modo da raggruppare i profili uguali, quindi evidenzio con colori diversi i vari gruppi.