Nella figura sottostante è mostrata una struttura a telaio (struttura composta da un sistema di elementi verticali, pilastri, ed elementi orizzontali, travi) e successivamente verrà dimensionata la trave più caricata con 3 materiali e tecniche costruttive diverse: Cemento Armato (CA), Acciaio e Legno.
DIMENSIONAMENTO DELLA TRAVE IN CEMENTO ARMATO:
ANALISI DEI CARICHI
Prendiamo in considerazione in 1 mq di solaio in laterocemento.
- Pavimento in Greso Porcellanto
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,4 kN/mq
- Massetto in Calcestruzzo alleggerito
dimensioni: (1m x 1m x 0,04m) densità = 18 Kn/mc
Q/mq = 0,72 kN/mq
- Isolante in pannelli di Fibra di Legno 140 SD
dimensioni: (1m x 1m x 0,04m) densità = 1,4 kN/mc
Q/mq = 0,056 kN/mq
- Soletta in cemento armato
dimensioni: (1m x 1m x 0,04m) densità = 25 kN/mc
Q/mq = 1 kN/mq
- Pignatte in laterizio
dimensioni: (40cm x 16cm x 2) densità = 5,5 kN/mc
Q/mq = 0,7 kN/mq
- Travetti in cemento Armato
dimensioni: (10cm x 16cm x 1m) densità = 25 kN/mc (x2 travetti)
Q/mq = 0,8 kN/mq
- Intonaco
dimensioni: (1m x 1m x 0,015m)
Q/mq = 0,3 kN/mq
sono stati utilizzati un calcestruzzo C 60/75 con una resistenza caratteristica fck =60 MPa ( Mpa = Mega Pascal)
e barre d'acciaio FeB 450C con una resistenza caratteristica di 450 MPa
che risultano avere resistenze di progetto di fcd = 19,83 Mpa e fyd = 391,30 MPa
Qs = Q travetti + Q soletta + Q pignattE
Qs = 0,8 kN/mq + 1 kN/mq + 0,7 kN/mq = 2,44 kN/mq
Qp = Q intonaco + Q isolante + Q massetto + Q pavimento + Q muri interni + Q impianti
Qp = 0,3 kN/mq +0,056 kN/mq +0,72 kN/mq +0,4 kN/mq +1 Kn/mq* +0,5 kN/mq* = 3,076 KN/mq = 2,98 kN/mq
Qa = 3 kN/mq
il carico ultimo risulta quindi essere:
Qu = (2,44 kN/mq * 1,3 + 2,98 kN/mq * 1,5 + 3 kN/mq * 1,5) x 6 (interasse) = 73,32 kn/mq
Per il dimensionamento della trave è stato utilizzato un foglio elettronico che considera:
- la struttura come una isostatica appoggiata - appoggiata
- Sollecitazione massima a Momento Flessionale in mezzeria della trave pari a q l^2/8
- resistenze caratteristiche e di progetto di calcestruzzo e acciaio
- la dimensione fissa della base della trave principale (b)
. Il Calcestruzzo e l’acciaio hanno un comportamento meccanico diverso, ma la deformazione di un punto della trave deve essere la stessa per via della Omogeneizzazione
ε(P)cls = ε(P)s
σ(P)cls x Ecls = σ(P)s x Es
dato che i Moduli elastici di acciaio e Cls sono diversi, viene introdotto un coefficiente di omogeneizzazione che è definito come il rapporto dei moduli elastici dei due materiali.
σ(P)cls = n σ(P)s
n viene considerato uguale a 15.
Per via dell’omogeneizzazione le tensioni di cls
Yn : hu = fcd : fyd
Dove:
Yn è l’asse neutro
hu è l’altezza utile. È il punto della sezione in cui si trovano le armature di acciaio.
Per l’omogeneizzazione fyd = come (fcd + fyd/n)
Yn : hu = fcd : (fcd + fyd/n)
Yn = hu x fcd/((fcd + fyd/n))
Consideriamo β come Il rapporto tra le resistenze cosi che la posizione dell’asse neutro risulti
Yn = β X hu
Quando una trave è soggetta a un carico perpendicolare al suo asse, si generano delle sollecitazioni di Momento. A causa del Momento si generano delle tensioni in ogni punto della sezione della trave. Una parte della sezione si comprime mentre una parte si tende.
Facendo l’equilibrio del momento possono presentarsi due possibiltà:
M = T x B M = C x B
Dalla risultante di Compressione è possibile determinare l’area di calcestruzzo, mentre dalla risultante di Trazione è possibile determinare l’area minima di Acciaio.
Il foglio di calcolo utilizzato di sotto dimensiona l’area di calcestruzzo.
Dando un valore fisso alla base della sezione e considerando la hu come incognita possiamo trovare l’altezza minima dalla trave H = hu + δ dove δ è il copriferro
Risulta una trave con altezza utile alte 43,79 cm e considerando un copriferro di 5 cm si ha un totale di 48,79 cm.
La sezione viene ingegnerizzata, e scelgo una trave con un altezza di 55 cm. Se guardiamo la seconda riga di calcolo,dove vengono rieseguiti i calcoli considerando nel carico ultimo l'aggiunta del peso della trave, l'aggiunta al carico strutturale di peso della trave, la sezione ingegnerizzata deve essere superiore di 50,37 cm.
DIMENSIONAMENTO DELLA TRAVE IN LEGNO LAMELLARE (PLATFORM FRAME):
ANALISI DEI CARICHI
Prendiamo in considerazione in 1 mq di solaio in PLATFORM FRAME che moltiplicato per la luce e l'interasse della trave Principale ci darà il carico dell'Area di influenza.
La figura mostra una sezione perpendicolare all'orditura dei travetti di OSB
- Pavimento in parquet in rovere
dimensioni: (1m x 1m x 0,02m) densità = 7,2 Kn/mc
Q/mq = 0,144 kN/mq
- Massetto in Calcestruzzo alleggerito
dimensioni: (1m x 1m x 0,04m) densità = 18 Kn/mc
Q/mq = 0,72 kN/mq
- Isolante in pannello EPS
dimensioni: (1m x 1m x 0,06m) densità = 0,25 kN/mc
/mq = 0,015 kN/mq
- Boarding panels OSB
dimensioni: (1m x 1m x 0,025m) densità = 8 kN/mc
Q/mq = 0,2 kN/mq
- Travetti
dimensioni: (0,12m x 0,05m x 1m) x 1,61 densità = 3,80 kN/mc
Q/mq = 0,037 kN/mq
Qs = Q travetti + Q boarding panels
Qs = 0,037 kN/mq + 0,2 kN/mq = 0,237 kN/mq
Qp = Q isolante + Q massetto + Q pavimento + Q muri interni + Q impianti
Qp = 0,015 kN/mq + 0,72 kN/mq + 0,144 kN/mq + 1 Kn/mq + 0,5 kN/mq
= 2,379 kN/mq
Qa = 3 kN/mq
il carico ultimo risulta quindi essere:
Qu = 50,26
il legno OSB ha una resistenza di 24 MPa
Il dimensionamento della sezione della trave avviene con lo stesso procedimento utilizzato per la sezione di acciaio.
Partendo dalla Formula di Navier
σ(y) = Mmax
Wx
Considerando che il Modulo di resistenza geometrica della trave W per una sezione rettangolare risulta essere
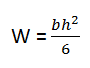
E fissando il valore della base della sezione b, risulta che l’altezza minima della sezione è
Il risultato ottenuto mostra che l'altezza minima devo essere di 59,52 cm, che ingegnerizzato danno un'altezza della trave di 60 cm.
DIMENSIONAMENTO DELLA TRAVE IN ACCIAIO:
ANALISI DEI CARICHI
Prendiamo in considerazione in 1 mq di solaio con lamiera grecata che moltiplicato per la luce e l'interasse della trave Principale ci darà il carico dell'Area di influenza.
- Pavimento in Greso Porcellanto
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,4 kN/mq
- Massetto in Calcestruzzo alleggerito
dimensioni: (1m x 1m x 0,04m) densità = 18 Kn/mc
Q/mq = 0,72 kN/mq
- Isolante in pannelli di Fibra di Legno 140 SD
dimensioni: (1m x 1m x 0,04m) densità = 1,4 kN/mc
Q/mq = 0,056 kN/mq
- Getto di completamento in il cemento armato
dimensioni: (1m x 1m x 0,04m) densità = 25 kN/mc
Q/mq = 1 kN/mq
- Lamiera Grecata Zincata
dimensioni: (10cm x 16cm x 1m)
Q/mq = 0,157 kN/mq
- IPE 100
dimensioni: (0,00103m^2 x 1m) densità = 78,5 kN/mc
Q/mq = 0,081 kN/mq
- Intonaco in cartongesso
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,078 kN/mq
Si progetta la trave Principale con un acciaio S275 con una resistenza carattestica fyk di 275 MPa con un coefficiente
γm0 = 1,05. La resistenza di progetto fyd = 261,90 MPa.
Qs = Q getto di completamento + Q lamieera + Q IPE100
Qs = 1 kN/mq + 0,157 kN/mq + 0,081 kN/mq = 1,238 kN
Qp = Q controsoffitto + Q isolante + Q massetto + Q pavimento + Q muri interni + Q impianti
Qp = 0,078 kN/mq + 0,056 kN/mq + 0,72 kN/mq + 0,4 kN/mq + 1 Kn/mq* + *0,5 kN/mq = 2,75 KN/mq
Qa = 3 kN/mq
il carico ultimo risulta quindi essere:
Qu = (1,24 kN/mq * 1,3 + 2,75 kN/mq * 1,5 + 3 kN/mq * 1,5) x interasse = 61,44 kn/mq
Formula di Navier
σ(y) = Mmax y
Ix
Per il dimensionamento della trave d'acciaio, si considera al posto di σ(y) la resistenza di progetto, per determinare sezione minima della trave. dove Mmax è il valore del Momento massimo, Ix è il momento di Inerzia della sezione e y è la distanza dall'asse neutro della sezione.
Per stabilire la Geometria della trave è importante ricordare che Wx = Ix/y dove Wx è un modulo di resistenza geometrico della trave

Il risultato del calcolo mostra come il Wx minimo della trave debba essere 1436,91 cm^3 dunque la sezione minima della trave risulta essere un IPE 450 con un Wx di 1500 cm^3.
Con l’ausilio di un foglio Excel vado ora a dimensionarmi la sezione del pilastro ed a ingenierizzarla conoscendo ora come trovare l’area minima e il momento di inerzia che mi servivano per dimensionare questo elemento strutturale soggetto a compressione nelle tre diverse tecnologie.
Sulla pianta di carpenteria, individuo il pilastro più sollecitato che sarà quello centrale e inquadro la sua area di influenza. Considero quindi la pianta di carpenteria del piano terra, poiché è quello più compressa dovendo supportare i carichi dei piani superiori, di un edificio tipo di 3 piani.
CEMENTO ARMATO
Per dimensionare la sezione del pilastro in cemento armato procedo come farò per il legno dal momento che entrambe hanno sezione piena rettangolare dunque posso trovare la base minima della sezione tramite il raggio di inerzia e secondo perché li tratto come materiali omogenei essendo molto reagenti a compressione. Unica differenza, nel C.A. ci sarà un passaggio in più che tiene conto del fatto che il pilastro in cemento armato è soggetto a presso-flessione e non a solo sforzo di compressione.
AREA DI INFLUENZA
In cui L1 e L2 sono le due luci della pianta
SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dal passaggio precedente e mi trovo il carico dovuto al peso proprio delle travi qtrave che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro
Trave principale = (0.30 x 0.55)m2 x 25 KN/m3 =4.125 KN/m
Trave secondaria= (0.30 x 0.55)m2 x 25 KN/m3=4.125 KN/m
Qtravi=(4.125x7) + (4.125x6) = 53.625 KN
Carichi strutturali qs = 2.50KN/m2
Carichi permanenti qp= 2.98 KN/m2
Carichi accidentali qa= 3 KN/m2
Qpiano: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza più l’aggiunta del contributo del peso delle travi
Qpiano = Qtravi+Qsolaio x area influenza = 566,8 KN
Numero piani= 3
Nmax= la forza di compressione N è dovuto al carico delle travi Qtravi più il carico del solaio Qsolaio per il numero di piani.
Nmax= 1700,595 KN
AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima.
fck è la resistenza caratteristica a compressione del calcestruzzo data dal tipo di cls scelto in questo caso 60 N/mm2. αcc è un coefficiente riduttivo pari a 0.85 e γc è il coefficiente di sicurezza per il cls pari a 1.5 .
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione : Fcd= αcc(fck/ γc) = 0.85(50/1.5)= 34 MPa
Amin= N/ Fcd=500,2 cm2
RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Grazie al raggio di inerzia minima e al fatto che la sezione del pilastro è rettangolare e piena posso trovarmi la base minima della sezione del pilastro.
E= modulo di elasticità 21000Mpa
β = 1 il pilastro è vincolato a terra tramite un incastro e nel nodo trave pilastro tramite sempre un incastro.
l= altezza del pilastro 3.5m
Con le formule che abbiamo dimostrato in classe il foglio di Excel mi calcola: λ max = ∏ √E/fcd ρmin= l0 /λ max
bmin= ρmin 2√3=14.18cm ingenierizzo a b=50cm
hmin=b/Amin =16.56 cm ingenierizzo a h=50cm
Una volta che ho base e altezza ingenierizzate della sezione del pilastro trovo l’area di design e il momento di inerzia di design
Adesign= bxh = 2500 cm2 Idesign= hxb3/12 =520833cm4
La sezione del pilastro più sollecitato è di 50cmx50cm ed è VERIFICATA avendo Adesign>Amin ed essendo h≥b
VERIFICA A PRESSO-FLESSIONE
Il pilastro essendo collegato alla trave con un incastro, in quel nodo trasmette un momento il quale potrebbe sottoporre il pilastro alla presso-flessione.
Per far si chè il pilastro non sia soggetto a presso flessione la tensione massima deve essere minore uguale alla tensione di progetto σmax ≤ fcd
- calcolo l’inerzia massima Imax= hxb3/12 =520833cm4
- calcolo il modulo di resistenza a flessione per le sezioni rettangolari
Wmax= bxh2/6=20833.33 cm3
- calcolo il carico distribuito sulla trave qt= qsolaio x Ls =73,32 KN/m
- calcolo il momento in testa al pilastro che è collegato alla trave
Mt= qt x L12 /12 = 299,39 KNxm
- infine trovo la tensione massima la quale deve essere minore di quella di progetto:
σmax=(N/A) +(Mt/Wmax) x 1000 =21,17 Mpa
VERIFICATA σmax ≤ fcd 21,17 < 34 Mpa
LEGNO
AREA DI INFLUENZA
Nuovamente L1 e L2 sono le due luci della pianta
SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dall’esercizio precedente e mi trovo il carico dovuto al peso proprio delle travi qtravi che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro x il numero delle travi che confluiscono nel nodo.
Trave principale = (0.35 x 0.60)m2 x 3,8 KN/m3 =0.798 KN/m
Trave secondaria= (0.35 x 0.60)m2 x 3,8 KN/m3=0.798 KN/m
Qtravi=(0.798x7) + (0.79x6) = 10,374 KN
Carichi strutturali qs = 0.24KN/m2
Carichi permanenti qp= 2.38 KN/m2
Carichi accidentali qa= 3 KN/m2
Qsolaio: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza
Qpiano = Qtravi+Qsolaio x area influenza = 362,418 KN
Numero piani= 3
Nmax = 1087, 25 kN
AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima.
Ho scelto un legno lamellare GL28h il mio coefficiente parziale di sicurezza γm=1.45.
Kmod: è un coefficiente che riduce i valori della resistenza che tiene conto della durata del carico e delle condizioni di umidità e cambia a seconda del materiale prescelto , nel mio caso: classe di servizio 2, classe di durata del carico media =0.80. Fc0,k è la resistenza a flessione caratteristica del legno = 28 Mpa
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione:
Fc0d= Kmod x Fc0,k / γm = 15.45 MPa
Amin= N/ Fc0d=703,8 cm2
RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Grazie al raggio di inerzia minima e al fatto che la sezione del pilastro è rettangolare e piena posso trovarmi la base minima della sezione del pilastro.
E= modulo di elasticità 8800Mpa
β = 1 il pilastro è vincolato a terra tramite un incastro e nel nodo trave pilastro tramite una cerniera/carrello
l= altezza del pilastro 3.5m
Con le formule che abbiamo dimostrato prima il foglio di Excel mi calcola: λ max = ∏ √E/fcd ρmin= l0 /λ max
bmin= ρmin 2√3=16.18cm ingenierizzo a b=30cm
hmin=b/Amin =23.46 cm ingenierizzo a h=50cm
Una volta che ho base e altezza ingenierizzate della sezione del pilastro trovo l’area di design e il momento di inerzia di design
Adesign= bxh = 1500 cm2 Idesign= hxb3/12 =112500cm4
La sezione del pilastro più sollecitato è di 30cmx50cm ed è VERIFICATA avendo Adesign>Amin ed essendo h>b
ACCIAIO
Per dimensionare un pilastro in acciaio con una sezione HEA si procede inizialmente come per il legno e per il c.a. in questo caso però non ho necessità di ricavarmi la base ma una volta trovato il raggio di inerzia mi calcolo l’inerzia minima e dopo di che posso andare sulle tabelle dei profilati e scegliere quello che ha l’inerzia maggiore di quella da me ottenuta.
AREA DI INFLUENZA
L1 e L2 sono di nuovo le due luci della pianta
Area influenza= 42 cm2
SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dall’esercizio precedente e mi trovo il carico dovuto al peso proprio delle travi qtravi che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro x il numero delle travi che confluiscono nel nodo.
La trave che avevo dimensionato nella parte precedente è un IPE 450 che ha un peso specifico di 78,5 KN/m3
Qtravi= 10,1 KN
Carichi strutturali qs = 1.24 KN/m2
Carichi permanenti qp= 2.75 KN/m2
Carichi accidentali qa= 3 KN/m2
Q1piano: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza e poi aggiungo il peso delle travi = 440,04 KN
Numero piani= 3
Nmax= la forza di compressione N è dovuto al carico Qsolaio per il numero di piani. Nmax= (440,04) x 3 = 1320,1 KN
AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima.
fyK è valore caratteristico di snervamento per l’acciaio che mi individua la classe di resistenza del materiale , in questo caso scelgo un acciaio medio (classe Fe430/s275) di resistenza 275 Nmm2.
γm coefficienti di sicurezza per la resistenza delle membrature e la stabilità pari a 1.05 .
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione:
Fyd= fyk/ γm = 275/1.05= 261.90 MPa
Amin= N/ Fyd=50.4 cm2
RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Trovo l’ Inerzia minima per poter cercare il mio profilato sulla tabella non prima di aver trovato dei valori importanti quali la snellezza e il raggio di inerzia.
E= modulo di elasticità 21000Mpa
β = 1 il pilastro è incernierato sia a terra che nel nodo trave pilastro.
l= altezza del pilastro 3.5m
λ max = ∏ √E/fcd ρmin= l0 /λ max Imin= A x ρmin2=780 cm4
Una volta che ho l’inerzia minima vado sulle tabelle dei profilati HEA e scelgo il profilato che abbia un Inerzia maggiore dell’ inerzia minima.
Una volta scelto il profilato ho l’area di design e il momento di inerzia di design.
Adesign= 53.8 cm2 Idesig=3692cm4 ρdesign=8.28 cm
Il profilato adatto per il pilastro è un HEA 200 VERIFICATO avendo Adesign>Amin
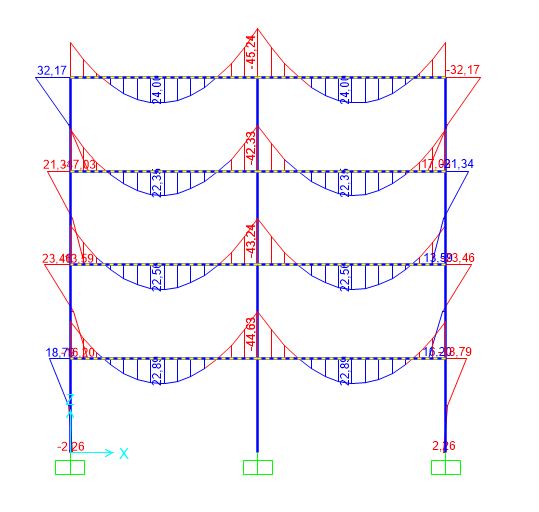
VERIFICA CON SAP
CLS
LEGNO
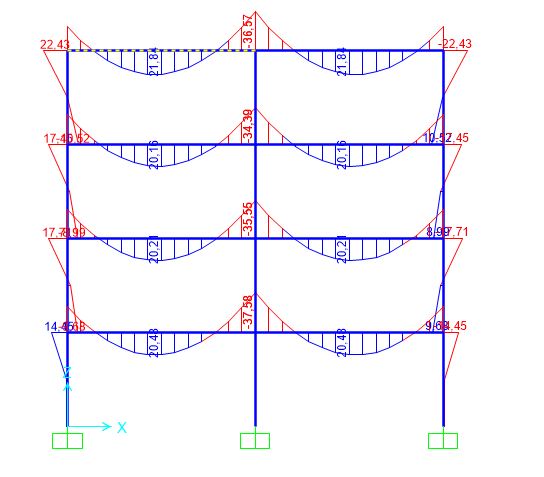
ACCIAIO
Commenti recenti