blog di Emanuele.Pizzi

CENTRO DELLE RIGIDEZZE

L’obiettivo dell’esercitazione è quello di studiare un piano dell’edificio di progetto e trovare la posizione del centro delle rigidezze e confrontarla con la posizione del centro delle masse.

Per avere un buon progetto strutturale i due centri devono essere coincidenti o più vicini possibile in modo che, in caso di sisma, vengano evitate rotazioni dell’impalcato.

Il piano è articolato secondo un telaio regolare in calcestruzzo armato nel quale si trovano due corpi scale/ascensore.

Su SAP definisco la griglia e disegno i pilastri, le travi e le superfici dei corpi scale/ascensori, attribuendo ad ogni elemento la corrispondente sezione in calcestruzzo armato. Assegno a tutti i punti di base dei pilastri e delle superfici il vincolo di incastro.

Traccio le diagonali della pianta e trovo, nell’intersezione, il centro geometrico che assumiamo come centro delle masse. In corrispondenza di questa intersezione inserisco un punto alla quota delle travi. Seleziono il punto e tutti gli altri punti che si trovano alla quota delle travi ed assegno la condizione di corpo rigido in modo che tutti i punti facciano parte dell’impalcato e che quest’ultimo non presenti al suo interno spostamenti e rotazioni relative.

Imposto una condizione di carico per calcolare il peso proprio dell’edificio ed effettuo l’analisi. Dalle tabelle di SAP ricavo tutte le reazioni vincolari verticali e sommandole ottengo il peso proprio, 3830,5 kN.

Definisco i carichi sismici come percentuali del peso proprio: essendo Roma una zona a basso rischio utilizzo il coefficiente 0,2 ed ottengo un valore di 766,1 kN.

Assegno 2 carichi concentrati orizzontali di valore 766,1 kN nel punto trovato come centro delle masse, uno in direzione x ed uno in direzione y: questi sono i carichi sismici.

Avvio l’analisi e osservo le deformate dell’impalcato prima per la forza in direzione x e poi per la forza in direzione y.

La deformata dovuta alla forza sismica lungo y non provoca rotazioni dell’impalcato.

La deformata dovuta alla forza sismica lungo x provoca una lieve rotazione dell’impalcato.

Spostando il centro delle masse verso il basso, quindi verso il centro di rotazione dell’impalcato, e riavviando l’analisi, cerco di trovare il punto in cui la rotazione si annulla. Questo punto è a soli 0,7 m dal centro delle masse.

GRATICCIO IN CALCESTRUZZO ARMATO

Progetto il graticcio in calcestruzzo armato per coprire uno spazio di 14x18 m appoggiandolo (tramite incastri) sui lati corti e avendo, quindi, una luce di 18 m. Le travi avranno tutte la stessa sezione poiché non ci sono gerarchie all’interno della struttura.

Al di sopra del graticcio avrò un solo piano occupato quasi interamente da una piccola biblioteca, per cui il sovraccarico accidentale q_a sarà di 5 kN/m² come da normativa (Categoria D2).

Definisco la stratigrafia di solaio e calcolo con il foglio Excel i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²).

Imposto una combinazione di carico assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali ed ottengo il carico totale q_u (kN/m²) di un piano.

Su Rhino disegno il graticcio con un interasse di 1 m tra le travi in entrambe le direzioni e lo importo su SAP.

Assegno ad ogni nodo dei due lati perimetrali lunghi 14 m il vincolo di incastro e assegno una sezione approssimativa di 30x70 cm a tutte le travi, utilizzando un calcestruzzo di classe C40/50.

In questo modo tengo subito conto, approssimativamente, del peso proprio delle travi che, trattandosi di calcestruzzo armato, è molto rilevante.

Assegno il carico q_u (kN/m²) suddividendolo tra le travi in entrambe le direzioni, quindi moltiplicandolo per 0,25 m per le travi di bordo e per 0,5 m per tutte le altre travi. I carichi distribuiti che avrò saranno, quindi, di 4,00625 kN/m per le travi di bordo e di 8,0125 kN/m per tutte le altre travi.

Avvio l’analisi e mi appare il graticcio nella configurazione deformata.

Osservando il diagramma dei momenti flettenti noto che corrisponde a quello di una trave doppiamente incastrata e dalla tabella degli sforzi trovo che il momento massimo si ha nella trave centrale e, precisamente, in corrispondenza dei due incastri e vale 701,952 kNm.

Sul foglio Excel inserisco il valore del momento flettente trovato per dimensionare correttamente la sezione della trave e, scegliendo un calcestruzzo di classe C40/50 e una base di 30 cm, ottengo un’altezza di 70 cm. È la sezione 30x70 cm usata già nel predimensionamento, è quindi verificata.

Stavolta osservo la deformata e dalla tabella degli spostamenti trovo che l’abbassamento massimo δ si ha nella trave centrale e, precisamente, al centro della campata e misura 0,024 m.

L’abbassamento deve essere inferiore all’abbassamento massimo ammissibile definito come un duecentesimo della luce: data la luce di 18 m, δ_max misura 0,09 m e quindi è verificato.

TELAIO IN CALCESTRUZZO ARMATO

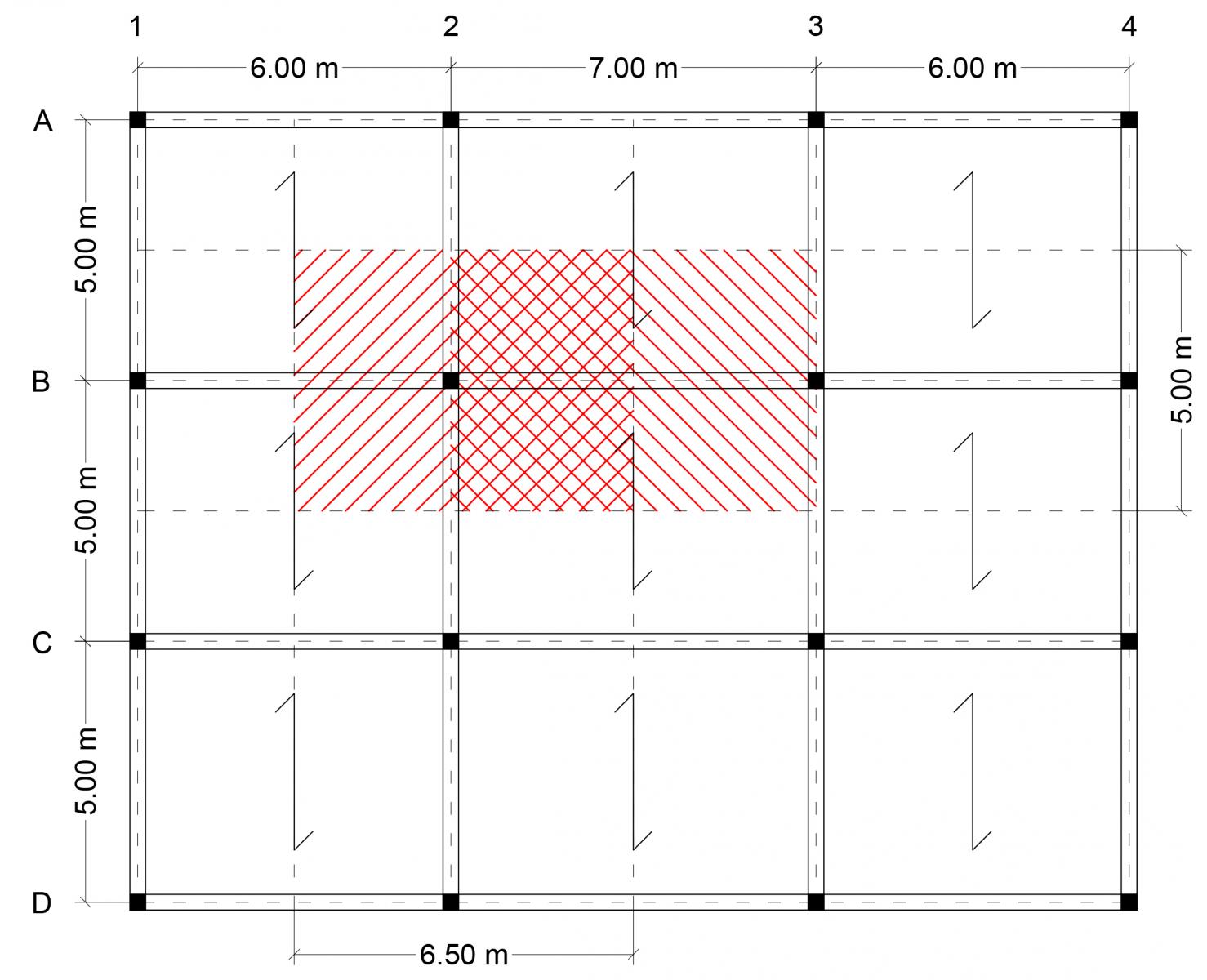
Progetto il telaio in calcestruzzo armato in Categoria B2 (Uffici aperti al pubblico) definendo la stratigrafia di solaio e andandone a calcolare con il foglio Excel i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²); il sovraccarico accidentale q_a è di 3 kN/m² come da normativa.

Dopo aver definito i carichi utilizzo il foglio Excel per dimensionare la trave maggiormente sollecitata a flessione, ovvero la trave di luce 7 m nella campata centrale, utilizzando lo schema statico della trave doppiamente appoggiata. Il momento flettente massimo in mezzeria è di 398,89 kNm e, scegliendo un calcestruzzo di classe C40/50 con una base di 30 cm, ottengo un’altezza della trave di 55 cm. Aggiungendo al carico strutturale q_s il peso proprio (kN/m) della trave ho verificato che la sezione 30x55 cm è adeguata a portare il carico q_u (kN/m).

Proseguo calcolando con il foglio Excel lo sforzo normale alla base (kN), utilizzando il modello della pilastrata, prendendo in considerazione il pilastro più sollecitato, ovvero quello centrale con area di influenza 6,5x5 m. Lo sforzo normale di un piano, dovuto al peso del solaio e delle travi che influiscono sul pilastro, è di 470,75 kN. L’edificio si eleva per 5 piani, quindi lo sforzo normale alla base è di 2353,75 kN.

Progetto il pilastro per un carico di 2353,75 kN utilizzando sempre un calcestruzzo di classe C40/50 e prendendo 3,5 m per l’altezza del pilastro e β=2 come condizioni di vincolo (asta incastrata ad una estremità e libera nell’altra). Per avere un raggio di inerzia minimo (cm) sufficientemente alto da impedire l’instabilità scelgo una base di 30 cm, per cui avrò un’altezza di 30 cm.

Disegno il telaio piano su SAP assegnando alla base dei pilastri del piano terra il vincolo di incastro. Assegno le sezioni 30x30 cm ai pilastri e 30x55 cm alle travi. Assegno a tutte le travi i carichi lineari q_s (kN/m), q_p (kN/m) e q_a (kN/m) e ai pilastri su un lato esterno il carico da vento preso come 0,7xinterasse kN/m; imposto una combinazione di carico q_u (kN/m) assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali e ai carichi da vento.

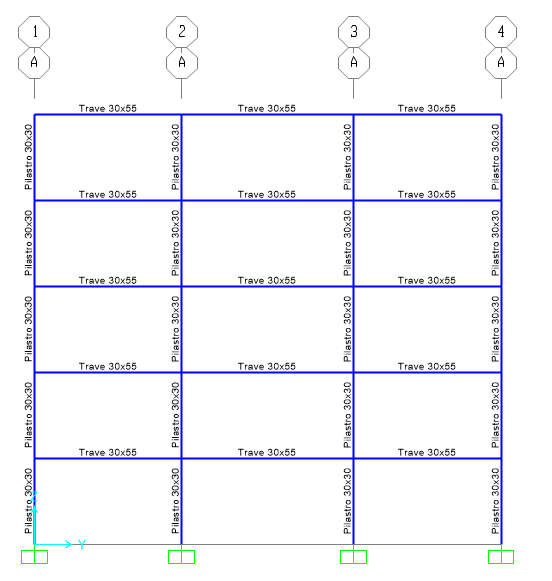
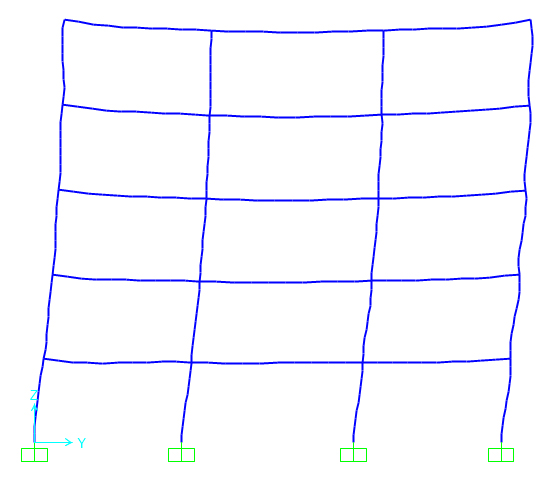
Avvio l’analisi e mi appare il telaio nella configurazione deformata.

Osservando i momenti flettenti sulle travi trovo che il momento massimo si ha nella campata centrale del piano terra e vale 285,43 kNm, quindi devo riprogettare la trave perché sovradimensionata. Sul foglio Excel imposto il nuovo momento flettente e, mantenendo la stessa base, trovo la nuova altezza per la trave pari a 45 cm.

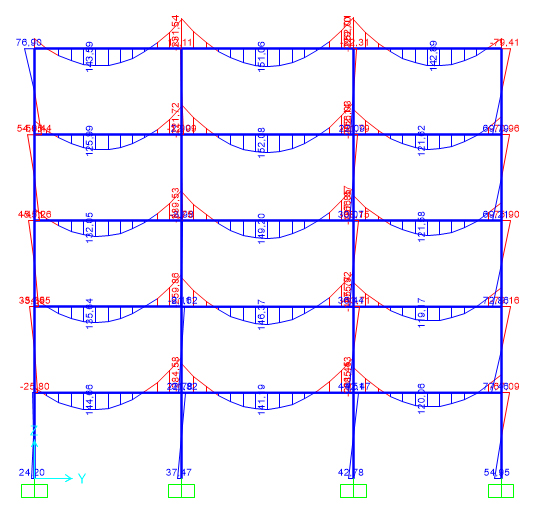
Su SAP sostituisco la sezione delle travi con la nuova sezione 30x45 cm e riavvio l’analisi. Stavolta osservo i pilastri del piano terra (che sono i più sollecitati poiché portano il carico di tutto l’edificio) tenendo conto sia dello sforzo normale (costante) sia del momento flettente (prendo il valore massimo), verificando quindi a pressoflessione. Calcolo, sul foglio Excel, le tensioni σ=(N/A)+(M/W) e noto che sono superiori alla tensione di progetto f_cd=28,33 MPa: aumentando la sezione dei pilastri da 30x30 cm a 35x35 cm e, quindi, aumentando l’area A (cm²) e il modulo di resistenza a flessione W (cm³), le tensioni σ nei pilastri scendono al di sotto della tensione di progetto f_cd e sono verificati.

TELAIO IN LEGNO

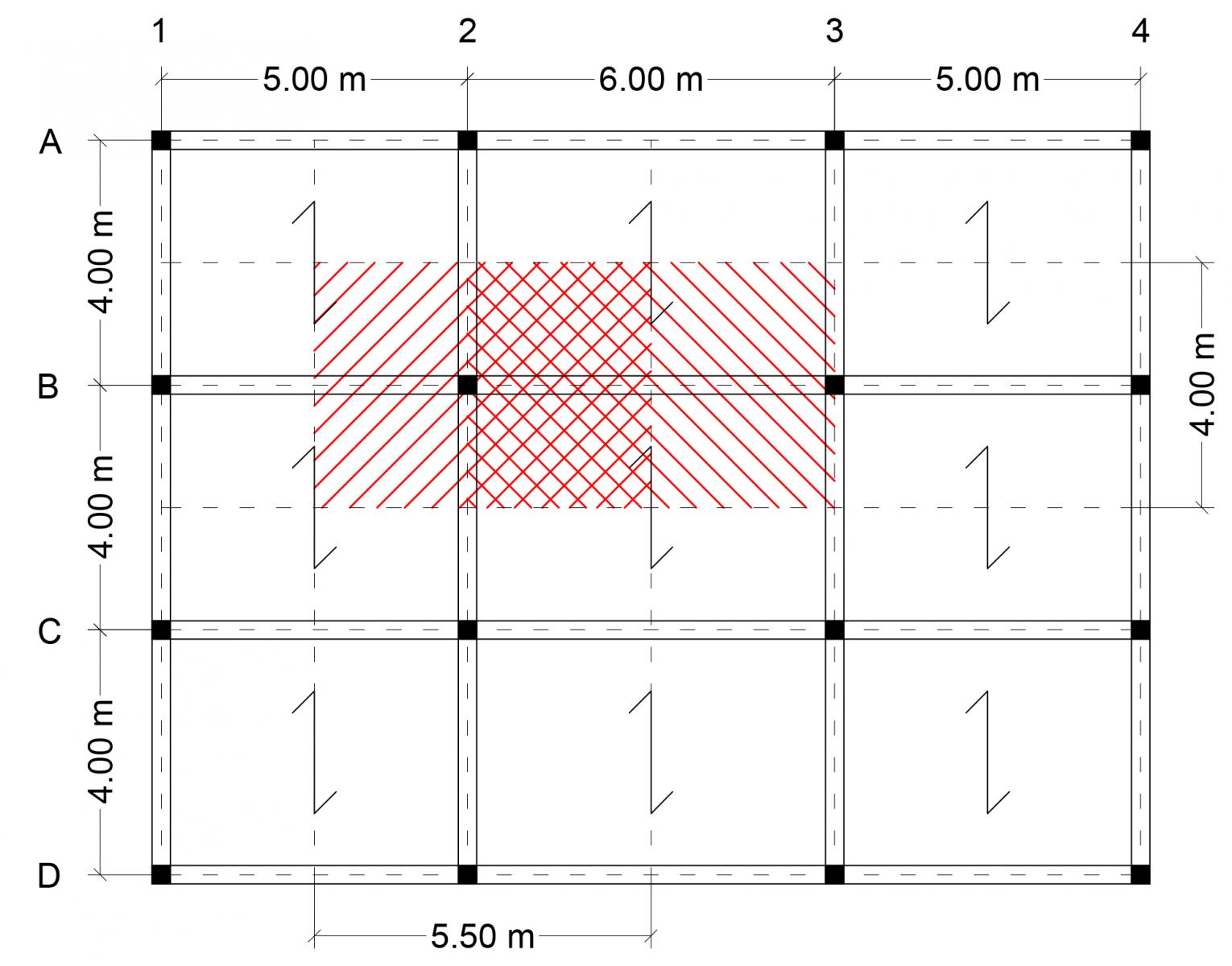
Progetto il telaio in legno in Categoria A (Ambienti ad uso residenziale) definendo la stratigrafia di solaio e andandone a calcolare con il foglio Excel i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²); il sovraccarico accidentale q_a è di 2 kN/m² come da normativa.

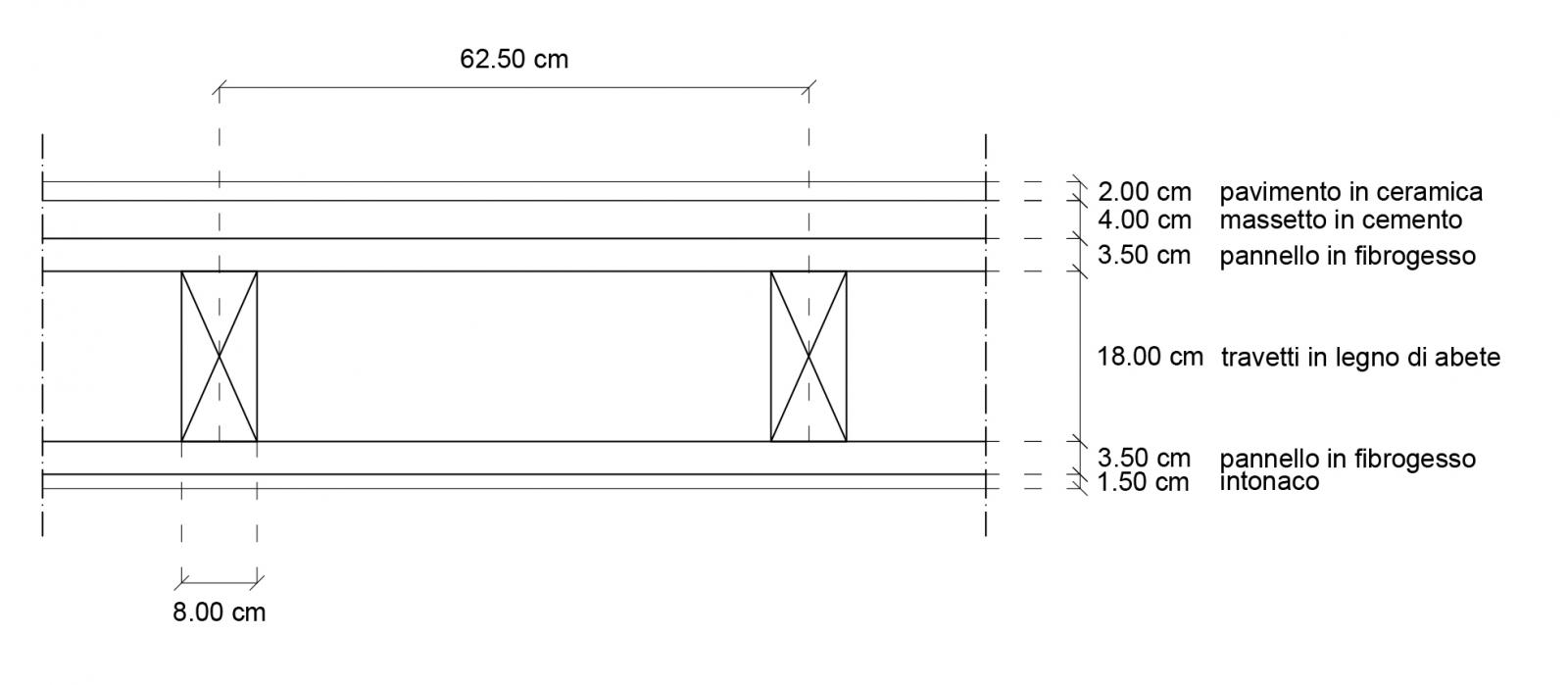
Dopo aver definito i carichi utilizzo il foglio Excel per dimensionare la trave maggiormente sollecitata a flessione, ovvero la trave di luce 6 m nella campata centrale, utilizzando lo schema statico della trave doppiamente appoggiata. Il momento flettente massimo in mezzeria è di 144,65 kNm e, scegliendo un legno d’abete di classe C24 con una base di 30 cm, ottengo un’altezza della trave di 50 cm. Aggiungendo al carico strutturale q_s il peso proprio (kN/m) della trave ho verificato che la sezione 30x50 cm è adeguata a portare il carico q_u (kN/m).

Proseguo calcolando con il foglio Excel lo sforzo normale alla base (kN), utilizzando il modello della pilastrata, prendendo in considerazione il pilastro più sollecitato, ovvero quello centrale con area di influenza 5,5x4 m. Lo sforzo normale di un piano, dovuto al peso del solaio e delle travi che influiscono sul pilastro, è di 185,347 kN. L’edificio si eleva per 5 piani, quindi lo sforzo normale alla base è di 926,734 kN.

Progetto il pilastro per un carico di 926,734 kN utilizzando sempre un legno d’abete di classe C24 e prendendo 3,2 m per l’altezza del pilastro e β=2 come condizioni di vincolo (asta incastrata ad una estremità e libera nell’altra). Per avere un raggio di inerzia minimo (cm) sufficientemente alto da impedire l’instabilità scelgo una base di 30 cm, per cui avrò un’altezza di 30 cm.

Disegno il telaio piano su SAP assegnando alla base dei pilastri del piano terra il vincolo di incastro. Assegno le sezioni 30x30 cm ai pilastri e 30x50 cm alle travi. Assegno a tutte le travi i carichi lineari q_s (kN/m), q_p (kN/m) e q_a (kN/m) e ai pilastri su un lato esterno il carico da vento preso come 0,7xinterasse kN/m; imposto una combinazione di carico q_u (kN/m) assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali e ai carichi da vento.

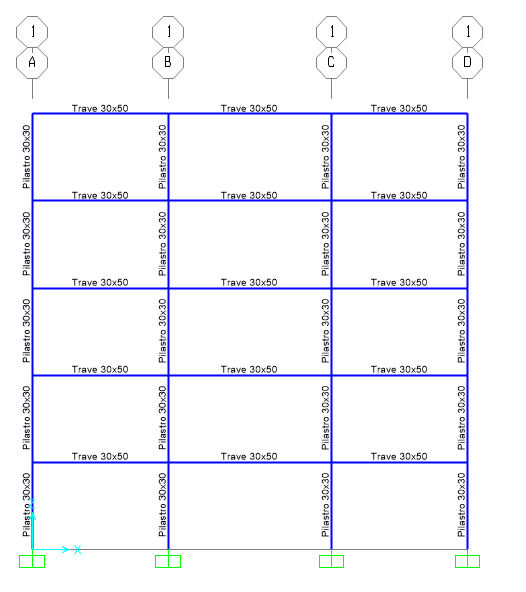
Avvio l’analisi e mi appare il telaio nella configurazione deformata.

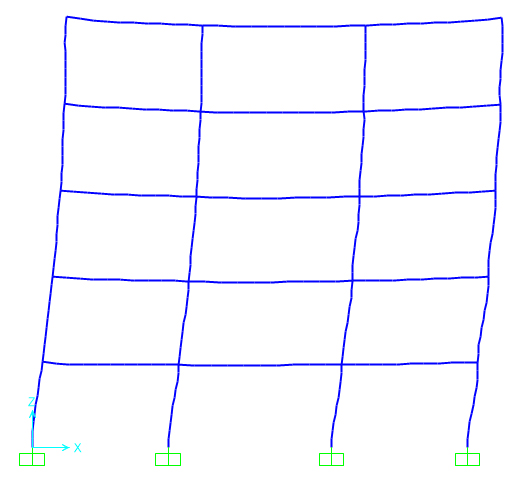
Osservando i momenti flettenti sulle travi trovo che il momento massimo si ha nella campata centrale del piano terra e vale 110,95 kNm, quindi devo riprogettare la trave perché sovradimensionata. Sul foglio Excel imposto il nuovo momento flettente e, mantenendo la stessa base, trovo la nuova altezza per la trave pari a 45 cm.

Su SAP sostituisco la sezione delle travi con la nuova sezione 30x45 cm e riavvio l’analisi. Stavolta osservo i pilastri del piano terra (che sono i più sollecitati poiché portano il carico di tutto l’edificio) tenendo conto sia dello sforzo normale (costante) sia del momento flettente (prendo il valore massimo), verificando quindi a pressoflessione. Calcolo, sul foglio Excel, le tensioni σ=(N/A)+(M/W) e noto che sono superiori alla tensione di progetto f_md=13,24 MPa: aumentando la sezione dei pilastri da 30x30 cm a 35x35 cm e, quindi, aumentando l’area A (cm²) e il modulo di resistenza a flessione W (cm³), le tensioni σ nei pilastri scendono al di sotto della tensione di progetto f_md e sono verificati.

TELAIO IN ACCIAIO

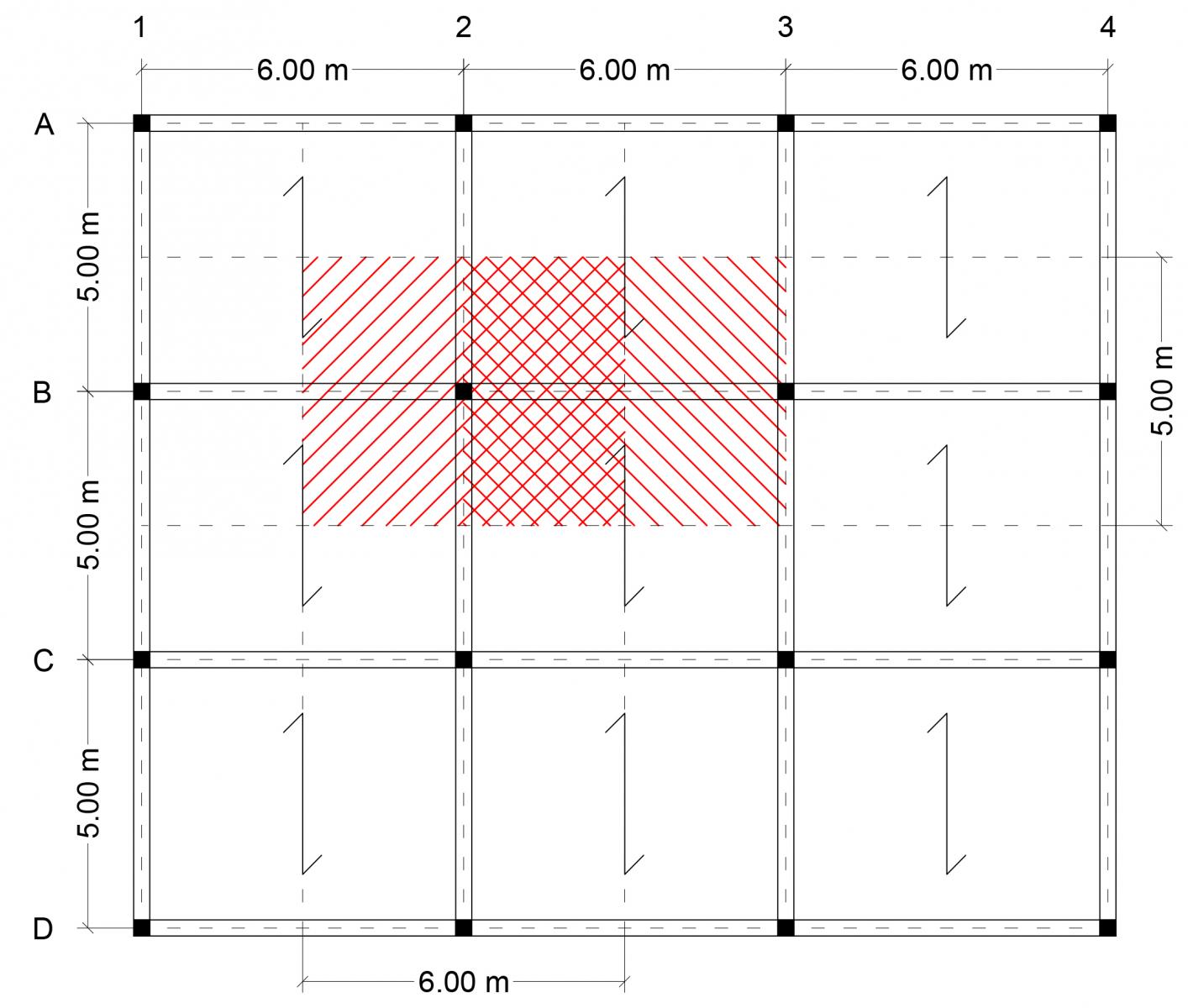
Progetto il telaio in acciaio in Categoria B2 (Uffici aperti al pubblico) definendo la stratigrafia di solaio e andandone a calcolare con il foglio Excel i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²); il sovraccarico accidentale q_a è di 3 kN/m² come da normativa.

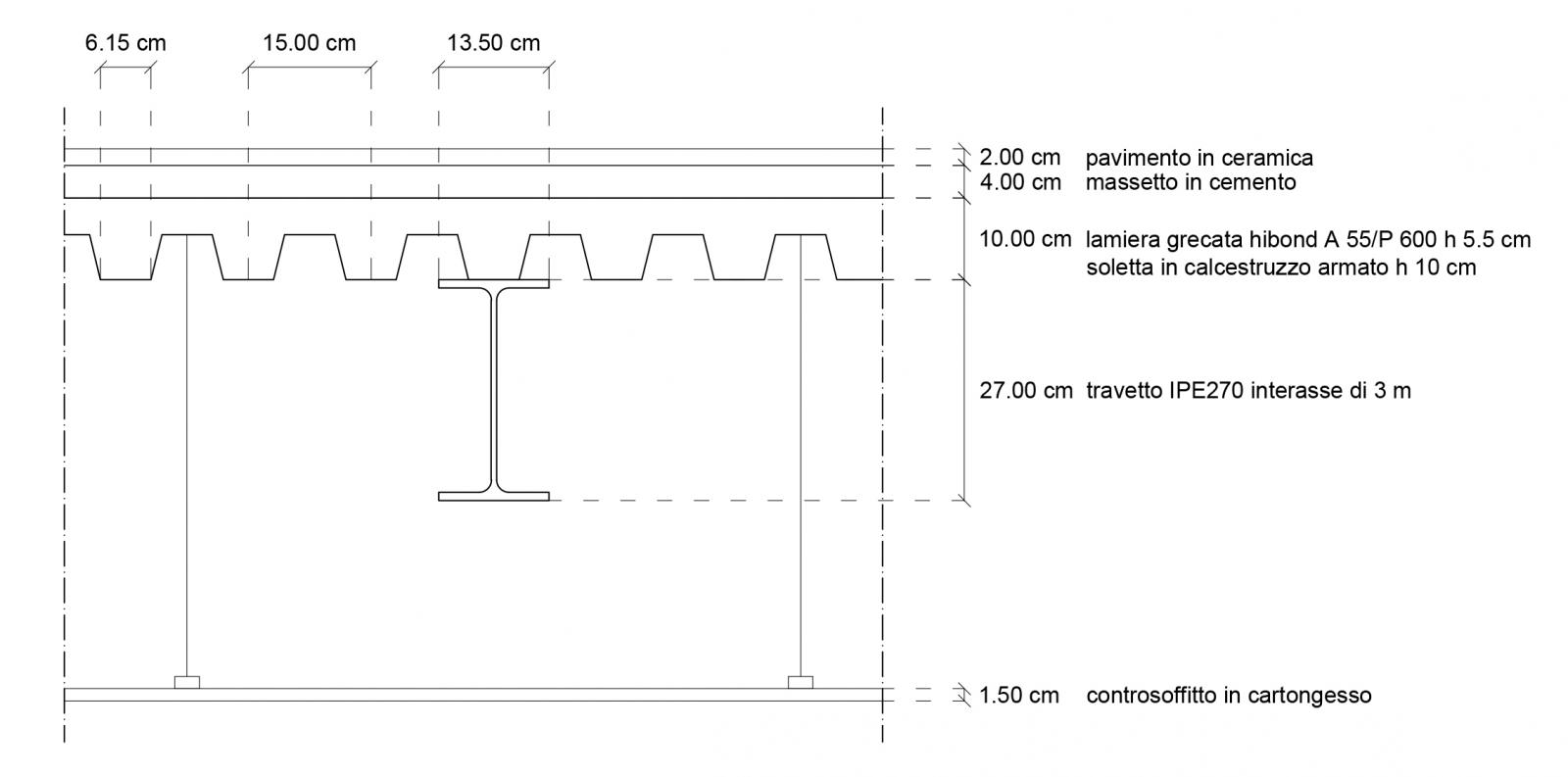
Dopo aver definito i carichi utilizzo il foglio Excel per dimensionare la trave maggiormente sollecitata a flessione, ovvero la trave di luce 6 m nella campata centrale, utilizzando lo schema statico della trave doppiamente appoggiata. Il momento flettente massimo in mezzeria è di 259,93 kNm e, scegliendo un acciaio di classe S275 ottengo un modulo di resistenza a flessione minimo W=992 cm³. Scelgo, quindi, un profilo IPE400 con W=1156 cm³. Aggiungendo al carico strutturale q_s il peso proprio (kN/m) della trave ho verificato che il profilo IPE400 è adeguata a portare il carico q_u (kN/m).

Proseguo calcolando con il foglio Excel lo sforzo normale alla base (kN), utilizzando il modello della pilastrata, prendendo in considerazione il pilastro più sollecitato, ovvero quello centrale con area di influenza 6x5 m. Lo sforzo normale di un piano, dovuto al peso del solaio e delle travi che influiscono sul pilastro, è di 353,87 kN. L’edificio si eleva per 7 piani, quindi lo sforzo normale alla base è di 2477,08 kN.

Progetto il pilastro per un carico di 2477,08 kN utilizzando sempre un acciaio di classe S275 e prendendo 3,2 m per l’altezza del pilastro e β=2 come condizioni di vincolo (asta incastrata ad una estremità e libera nell’altra). Per avere un raggio di inerzia minimo (cm) sufficientemente alto da impedire l’instabilità e un’area minima (cm²) per resistere alla rottura del materiale scelgo un profilo HEB300.

Disegno il telaio piano su SAP assegnando alla base dei pilastri del piano terra il vincolo di incastro. Assegno le sezioni HEB300 ai pilastri e IPE400 alle travi. Assegno a tutte le travi i carichi lineari q_s (kN/m), q_p (kN/m) e q_a (kN/m) e ai pilastri su un lato esterno il carico da vento preso come 0,7xinterasse kN/m; imposto una combinazione di carico q_u (kN/m) assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali e ai carichi da vento.

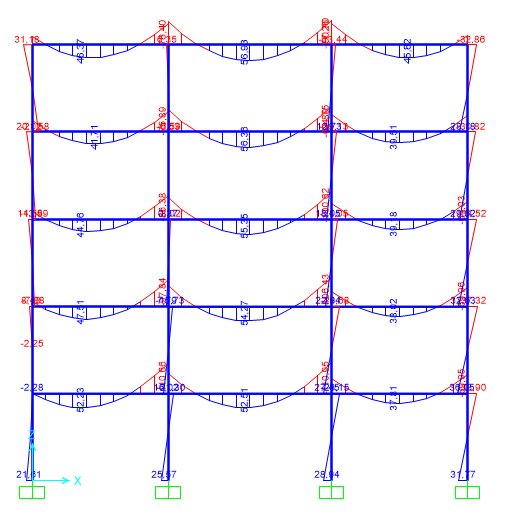
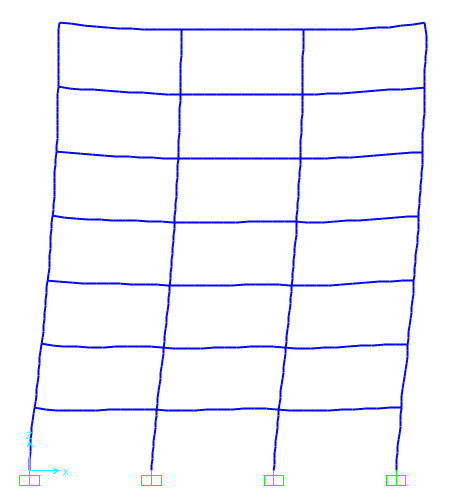
Avvio l’analisi e mi appare il telaio nella configurazione deformata.

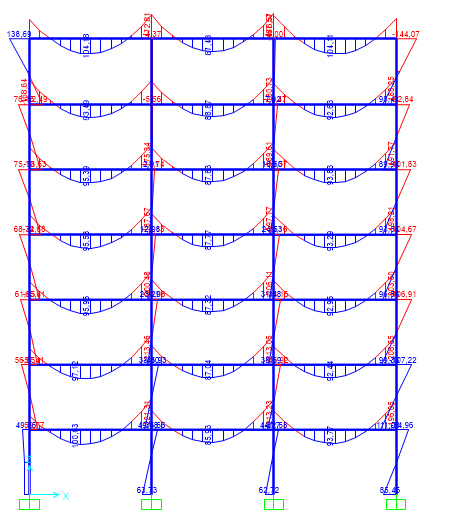
Osservando i momenti flettenti sulle travi trovo che il momento massimo si ha nella campata laterale (esposta all’azione del vento) del piano terra e vale 221,31 kNm, quindi devo riprogettare la trave perché sovradimensionata. Sul foglio Excel imposto il nuovo momento flettente e trovo il nuovo modulo di resistenza a flessione minimo W=845 cm³ e scelgo un profilo IPE360 con W=903,6 cm³.

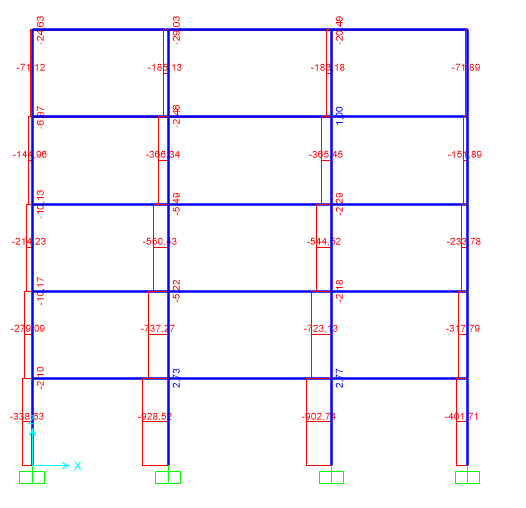
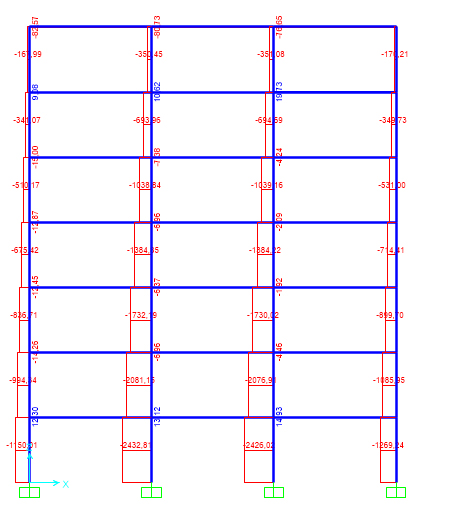
Su SAP sostituisco la sezione delle travi con la nuova sezione IPE360 e riavvio l’analisi. Stavolta osservo i pilastri del piano terra (che sono i più sollecitati poiché portano il carico di tutto l’edificio) tenendo conto sia dello sforzo normale (costante) sia del momento flettente (prendo il valore massimo), verificando quindi a pressoflessione. Calcolo, sul foglio Excel, le tensioni σ=(N/A)+(M/W) e noto che sono inferiori alla tensione di progetto f_yd=261,90 MPa; i pilastri sono verificati.