blog di jessica.sordi

La terza esercitazione consiste nell’analisi di un telaio di un piano di un edificio, in questo caso il nostro, in particolare individuando il centro di massa e il centro delle rigidezze. Un buon progetto strutturale prevede che i due centri siano coincidenti o più vicini possibile in modo che, all'agire di forze orizzontali, vengano evitate rotazioni dell’impalcato.

Per realizzare il piano tipo ho importato da autocad una griglia di riferimento in cui ho incluso gabbie ascensori e corpi scala.

Realizzato un sistema di travi e pilastri, ho disegnato delle aree poligonali lì dove dovevo definire dei setti.  Alla base di ogni pilastro e di ogni punto appartenente ai setti ho posto un incastro.

Sezioni degli elementi in calcestruzzo :

• pilastri circolari → d = 60 cm
• travi → 70x45 cm
• setti → 30x30 cm

Per determinare il centro di massa (o centro d'area) ho suddiviso il trapezio in due triangoli, posizionando i due centri d’area nei baricentri. Ottenute le coordinate dei due centri ho trovato, tramite le formule seguenti, le coordinate del centro dell’intera figura:

                                                       G_x = (A₁x₁ + A₂x₂ ) / (A₁+A₂)

                                                       G_y = (A₁y₁ + A₂y₂) / (A₁+A₂)

Posizionato il centro di massa, al piano z=3, ho assegnato una condizione di vincolo interno Diaphragm per imporre la rigidezza del telaio, incluso il centro di massa che deve far parte dell’impalcato riproducendo la condizione di impalcato rigido.

Per impostare l’analisi devo conoscere il valore delle forze orizzontali che devo applicare al centro di massa e per farlo devo considerare il peso totale dell’edificio e moltiplicarlo per un coefficiente sismico di massima pari a 0,2.

Per trovare il peso dell’edificio eseguo l’analisi dell’impalcato considerando esclusivamente il peso proprio, dalle tabelle di analisi trovo il valore della forza verticale che, sommata in tutte le sue componenti, mi fornisce il peso totale dell’edificio 44712,35 kN; moltiplicato per 0,2 da 942,47 kN, ovvero l’intensità della forza orizzontale che devo applicare. 

Avvio l’analisi e osservo le deformate dell’impalcato prima per la forza in direzione x e poi per la forza in direzione y.

La deformata dovuta alla forza orizzontale provoca una rotazione dell’impalcato direzione x.

La deformata dovuta alla forza orizzontale provoca una rotazione dell’impalcato anche in direzione y.

La rotazione mette in evidenza il fatto che il centro di massa non coincide con quello delle rigidezze.

Sposto il centro di massa verso il basso e riavviando l’analisi cerco di trovare il punto in cui la rotazione si annulla. Si abbassa in totale di 5,80 m.  

Risultato direzione x

Risultato direzione y

In collaborazione con Veronica Stefanelli.

Graticcio

Progetto un graticcio in CA, dimensioni 10x15 m, maglia 1x1 m. Incastrato,in appoggio, lungono i lati corti mi darà una luce libera di 15 m. Le travi avranno tutte la stessa sezione, poichè lo schema a graticcio non prevede gerarchia tra di esse.

La stratrigrafia del solaio mi darà i carichi strutturali q_s (kN/m²) e i sovraccarichi permanenti q_p (kN/m²), il carico accidentale è definito dalla destinazione d'uso,in questo caso uffici e sarà q_a=3 kN/m²

q_s = 3,58 kN/m²            q_p = 2,264 kN/m²      q_a=3 kN/m²

La combinazione di carico si otterrà assegnando i coefficienti di sicurezza 1,3 al carico strutturale e 1,5 ai sovraccarichi permanenti e accidentali.

                                                                q_u = 12,414 kN/m²   (1 piano)

Una volta definita la geometria e il carico importo il disegno fatto su Autocad in SAP.

Assegno i vincoli di incastro ai nodi nei lati corti (10m) e una sezione approssimativa a tutte le travi di 25x50 cm, considerando un cls di classe C 40/50.

Assegno poi il carico distribuito alle travi. Le travi ai bordi avranno metà del carico quindi 6,20 kN/m e le travi centrali il carico pieno 12,414 kN/m.

Avvio l'analisi e mi compare la configurazione indeformata.

Il diagramma dei momenti flettenti corrisponde a quello di una trave doppiamente incastrata. 

Estraggo dalle tabelle il valore del momento massimo che corrisponde a 260,58 kN·m e lo inserisco nella tebella per il dimensionamento corretto della sezione. Verifico, in questo caso che la sezione scelta è corretta. 

Dalla deformata trovo che l’abbassamento massimo δ si ha nella trave centrale e misura 0,0576 m. L’abbassamento deve essere inferiore all’abbassamento massimo ammissibile definito come 1/200 della luce: data la luce di 15 m, δ_max misura 0,075 m e quindi è verificato.

Per la prima esercitazione abbiamo fatto l’analisi di un telaio a pilastrata con tecnologia in cemento armato, acciaio e legno. Le immagini che seguono descrivono il telaio preso in esame: 

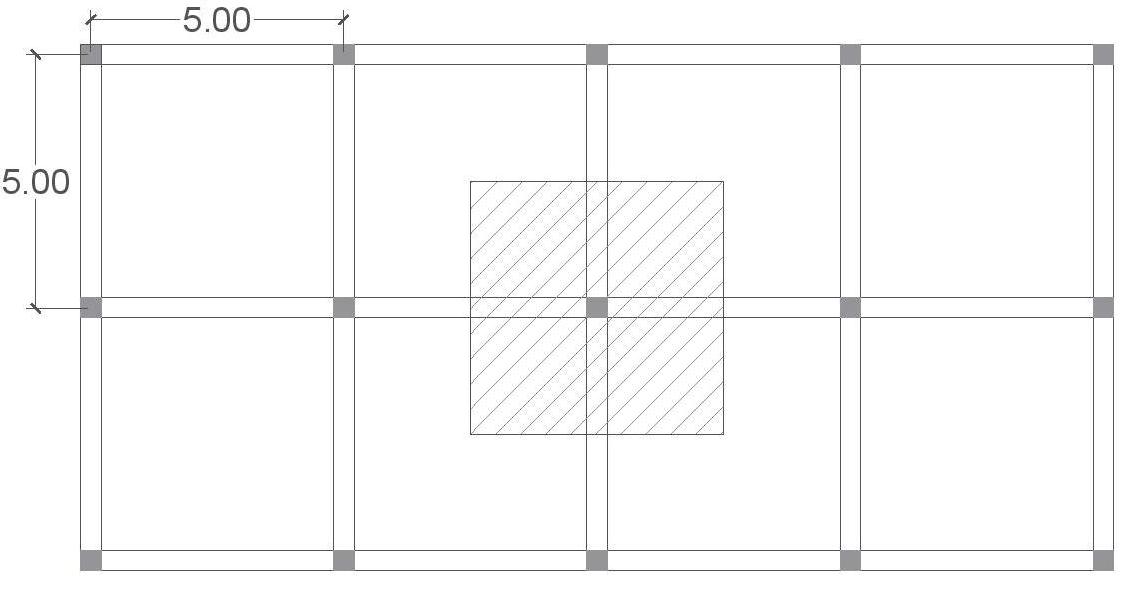
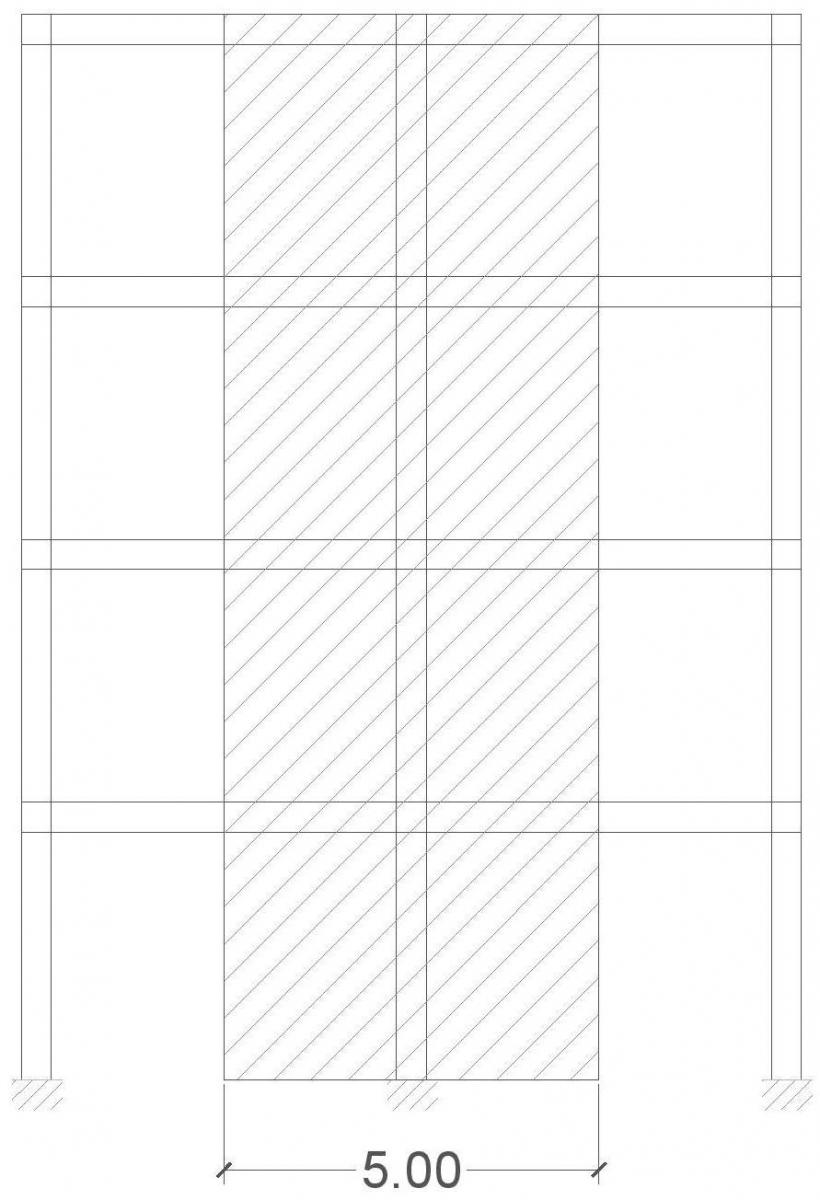
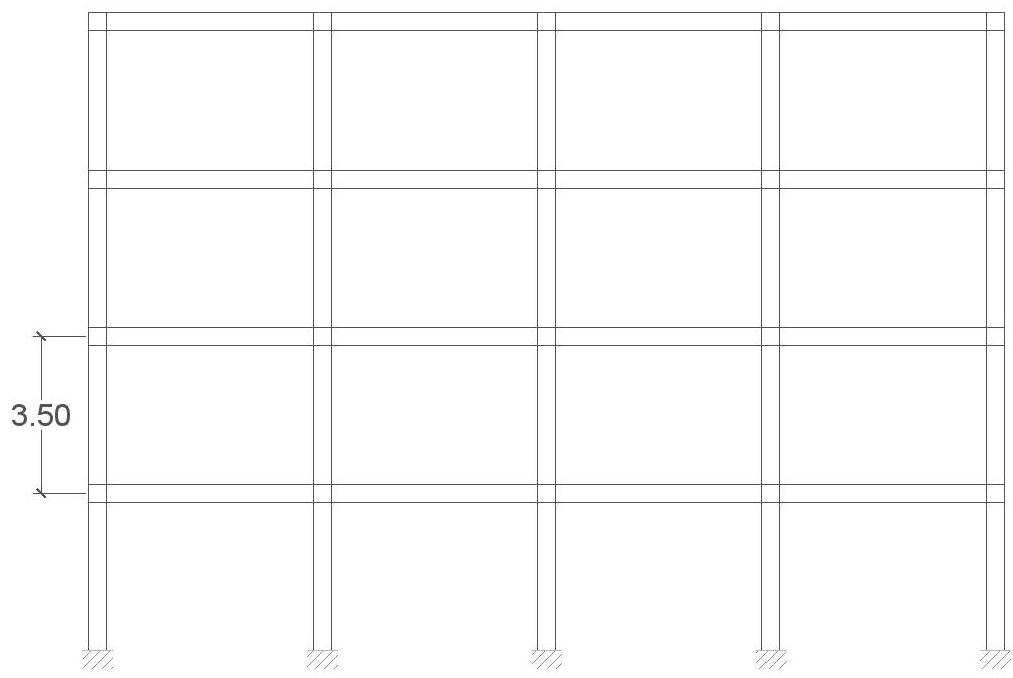
Abbiamo realizzato due analisi parallele, tramite i fogli Excel, una sul progetto della trave e una sul progetto del pilastro. Definito l’interasse, abbiamo analizzato la combinazione di carico q_u, ottenuta come somma delle singole componenti di carico q_s, q_p e q_a, che sono rispettivamente il peso della struttura a m² (che dipende dalla tecnologia usata), il peso dei sovraccarichi permanente e il carico accidentale dovuto alla destinazione d’uso (nel nostro caso uffici), ognuno di essi moltiplicato per un fattore di sicurezza.

Solai scelti divisi per tecnologia:

LATERO-CEMENTO

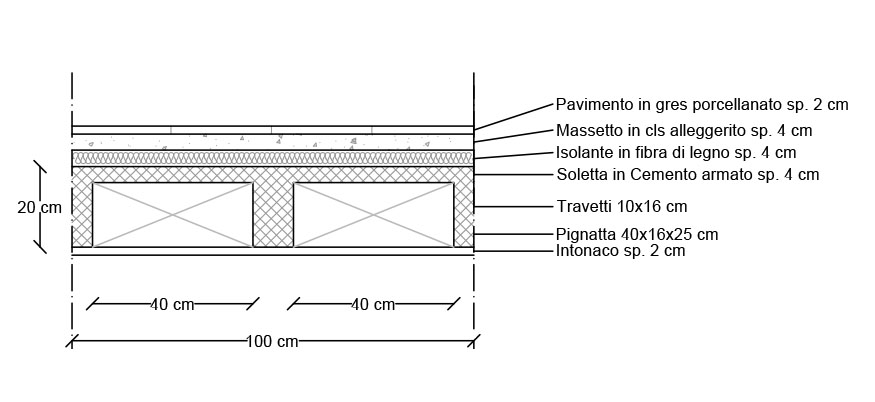
ACCIAIO

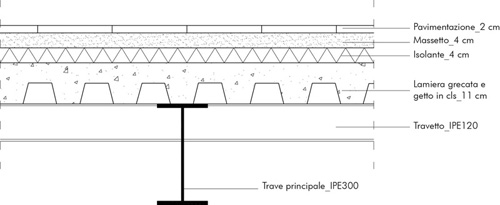
LEGNO

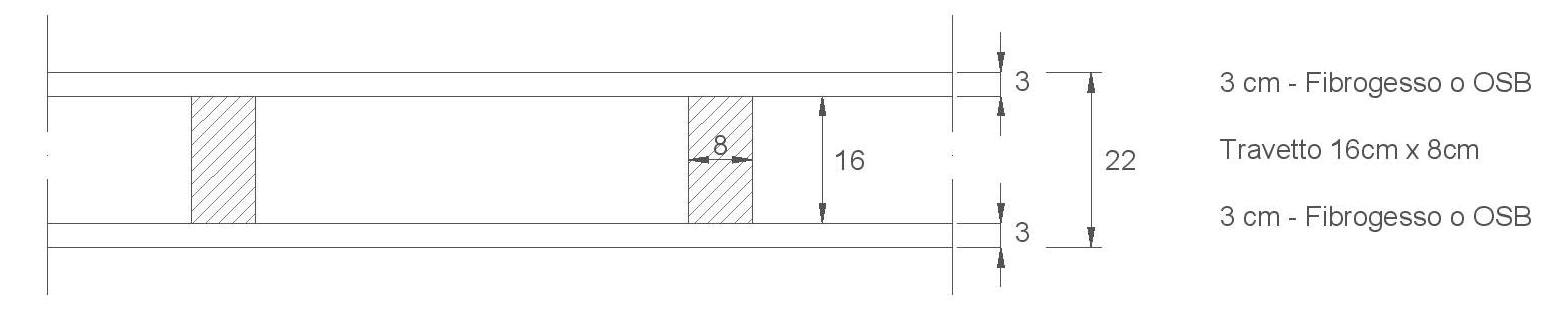
TRAVE

Nel primo foglio Excel di calcolo della trave abbiamo portato parallelamente l’analisi delle tre tecnologie per arrivare alla combinazione di carico:

                                                 q_{u =} q_sγ_s·q_pγ_p·q_aγ_a

                                                           γ_s=1.3

                                                           γ_p=1.5

                                                           γ_a=1.5

Questa operazione ci fornisce un dato al m². Per effettuare l’analisi lungo la trave moltiplichiamo per l’interasse per ottenere quindi una grandezza espressa in kN/m. L'obiettivo questo primo foglio é trovare il momento massimo  che agisce sulla trave, per cui aggiungiamo l’informazione relativa alla luce e, ipotizzando il modello di funzionamento di trave appoggiata, calcoliamo il valore di M_max con la seguente formula: 

                                                          M_{max =} q·l²/8

Con questo dato di partenza abbiamo sviluppato le tre pagine per le tre tecnologie, per quanto riguarda il predimensionamento della trave ed abbiamo ottenuto come dato in uscita il valore di base e altezza, quindi definito la sezione.

In particolare per il calcestruzzo abbiamo stabilito una tensione caratteristica f_y,k di 450 MPa, l’abbiamo moltiplicata per il coefficiente di sicurezza per ottenere la tensione di progetto f_y,d per i tondini di acciaio; abbiamo preso f_c,k per la tensione caratteristica del calcestruzzo che va moltiplicata per un coefficiente αα che tiene conto dell’interazione del tempo e dell’ambiente con la struttura, e diviso per il coefficiente γ di sicurezza per ottenere f_c,d di progetto. 

Per la definizione della sezione effettuiamo i seguenti passaggi:

• calcoliamo il valore di β come:      β = f_c,d /(f_c,d+(f_y,d/15))
• calcoliamo il valore di r come:       r = (2 / β (1-β/3))^^0.5
• ipotizziamo una base:                   b = 30 cm
• calcoliamo l’altezza utile:              h_u= r (M_max/ f_c,d·b)^^0.5
• inseriamo un copri ferro:               δ = 5 cm
• calcoliamo l’altezza effettiva della sezione sommando l’altezza utile con la dimensione del copri ferro ed otteniamo un’altezza ingegnerizzata pari a 40 cm.
• Calcoliamo l’area della sezione della trave e il suo peso unitario moltiplicando l’area per il peso specifico del calcestruzzo (30 x 40 cm). 

Per l’acciaio abbiamo stabilito f_y,k pari a 275 MPa, la tensione caratteristica di snervamento, da dividere per il coefficiente di sicurezza pari a 1.05 che ci permette di ottenere la tensione di progetto dell’acciaio, f_y,d. Abbiamo poi calcolato il modulo di resistenza a flessione:                                

                                                            W_x,min= M_max / f_y,d

Con questo dato andiamo nel sagomario e prendiamo una IPE che ne abbia uno maggiore (nel nosto caso IPE 330).

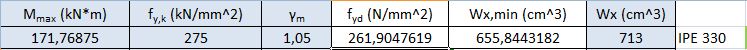
Allo stesso modo per il legno abbiamo stabilito la tensione caratteristica f_m,k (C30), moltiplicando questa per il coefficiente di sicurezza k_mod ,che tiene conto dell’umidità e dell’effetto della durata del carico, e dividendolo per un coefficiente di sicurezza pari a 1.50 otteniamo la tensione di progetto f_{d :}

                                                           f_d = f_m,k / γm · k_mod

Ipotizziamo anche in questo caso una base e calcoliamo l’altezza utile con la seguente formula:             

                                                            h_u= (6·M_max/(b· f_d)

Ingegnerizzando questo valore otteniamo il valore finale dell’altezza della sezione (30 x 45 cm).

PILASTRO

Come prima analisi abbiamo realizzato una pagina per il calcolo dello sforzo normale agente sul pilastro che poi diventa nelle successive tre pagine il dato di partenza per la definizione della sezione. In particolare abbiamo definito:

area di influenza A_{inf :}                  A_inf = (L_a + L_b/2)+(L_c+L_d/2)

Fissiamo i tre γ pari a 25 kN/m³ per il calcestruzzo, 78.5 kN/m³ per l’acciaio e  6 kN/m³ per il legno.Calcoliamo l’area della trave e quindi il loro peso, moltiplicando l’area della trave per una luce (per ottenere il peso delle travi principali) e la stessa area per l’altra luce (per ottenere il peso delle travi secondarie), questa somma moltiplicata per il peso specifico ci fornisce il peso delle travi su un m² di solaio.

Calcoliamo la combinazione di carico, come abbiamo fatto precedentemente nelle travi con la formula:

                                                      q_u = q_sγ_s·q_pγ_p·q_aγ_a

Calcoliamo il valore di sforzo normale agente su un piano moltiplicando l’area di influenza per la combinazione di carico allo stato limite ultimo e lo sommiamo al peso delle travi, ottenendo il valore concentrato di N (kN):

                                                       N = (Ainf · q_u ) + q_t

Stabilito il numero dei piani (per noi 4) otteniamo il valore di massima sollecitazione a compressione agente sul pilastro più sollecitato moltiplicando l’N agente su un piano per il numero di piani. Con questo dato entriamo nella progettazione dei pilastri nelle tre tecnologie.

La progettazione della sezione di un pilastro in calcestruzzo prevede oltre la progettazione a compressione anche una verifica a pressoflessione che aggiungiamo alla fine di questa analisi a differenza delle altre tecnologie. 

Stabiliamo la classe di resistenza del calcestruzzo (C50/60) e ottengo il valore della resistenza di compressione di progetto moltiplicando il valore della resistenza caratteristica per un coefficiente αα (0.85), che tiene conto degli effetti del tempo, e dividendolo per il coefficiente di sicurezza che tiene conto del processo produttivo γ_m pari a 1,5. 

Calcoliamo l’area minima considerando la formula inversa di σ = N/A quindi:

                                                                        A_min = N_max/f_c,d

Stabiliamo il modulo elastico E, l’altezza del pilastro L e il coefficiente β che tiene conto della condizione di vincolo della struttura, che abbiamo ipotizzato pari ad 1.

Abbiamo calcolato la snellezza:                       λ = ( π² · E/ f_c,d)

Il raggio giratore d’inerzia:                                ρ_min = L·β / λ

Base minima:                                                    b_min =  ρ_min (12)^{^0.5}

Quindi otteniamo l’altezza minima dividendo l’area minima per la base minima; ingegnerizziamo le dimensioni ottenute, calcoliamo l’area della sezione, il momento d’inerzia I e il modulo di resistenza W pari a:

                                                                          W_max=b·h²/6

Per la sezione in calcestruzzo effettuiamo la verifica a pressoflessione confrontando la σ_max  con la tensione di progetto: 

                                                                          σ_max = (N_max/A) + (M_max/W)

Il valore di M_max è calcolato come                  Mt = q_t·L_p²/12

 dove q_t è il valore uscente dal progetto della trave in calcestruzzo e che è pari alla combinazione di carico per l’interasse principale.

La verifica è soddisfatta se questo valore di tensione massima è minore di quella di progetto. 

Per quanto riguarda il progetto del pilastro in acciaio abbiamo definito la classe di resistenza f_y,k (235 MPa), che moltiplicato per il coefficiente di sicurezza (1.05) ci consente di calcolare la tensione di progetto f_y,d. Successivamente: 

• Calcoliamo l’area minima dividendo lo sforzo N massimo per la tensione di progetto
• Stabiliamo il modulo elastico E (210000 MPa), il β che descrive i vincoli e l’altezza del pilastro (3.50 m).
• Calcoliamo la snellezza minima 

                                                             λ_min=( π² · E/ f_y,d)

• Calcoliamo il ρ_min

                                                             ρ_min= L·β / λ

A differenza del calcestruzzo, nell’acciaio non calcoliamo l’altezza utile ma cerchiamo il valore d’inerzia minimo che possiamo andare a trovare nei sagomari delle HEA con la condizione  che il valore dell'inerzia della sezione scelta sia maggioredi quella di progetto.

                                                             I_min =Aρ_min

Stabilito il profilo HEA (200) inseriamo nella tabella i valori che ne descrivono la sezione, quindi l’area, l’inerzia e il raggio giratore d’inerzia. Verifichiamo poi che la snellezza che otteniamo sia minore della snellezza minima che abbiamo calcolato precedentemente.

Il progetto del pilastro in legno segue le seguenti fasi.

• Scegliamola classe di resistenza (C24)
• Riportiamo il valore della tensione caratteristica, che moltiplicata per il coefficiente k_mod  che tiene conto dell’umidità e dell’effetto della durata del carico,e divisa per il coefficiente di sicurezza γ_m, ci da la tensione di progetto.
• Dividiamo lo sforzo normale agente per la tensione di progetto otteniamo l’area minima della sezione.
• Stabiliamo il modulo elastico E, il coefficiente β e l’altezza del pilastro L.
• Calcoliamo quindi la snellezza massima λ_max, il ρ_min e otteniamo 

                                                                         b_min =  ρ_min (12)^{^0.5}

Stabiliamo una base ingegnerizzata, ricaviamo dividendo l’area minima per quest’ultima base ed ingegnerizziamo anch’essa. Stabilita quindi la sezione otteniamo l’area di progetto e il valore dell’inerzia. 

Finita la fase di calcolo su Excel abbiamo impostato questo stesso telaio, nelle tre tecnologie, nel software SAP2000, che ci consente di poter confrontare le sezioni progettate e i relativi diagrammi delle sollecitazioni con ciò che abbiamo ottenuto dai fogli di calcolo.

Diagrammi calcestruzzo:

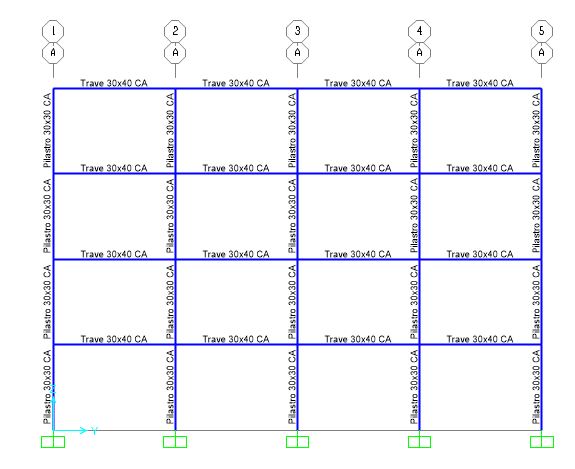
Schema strutturare CA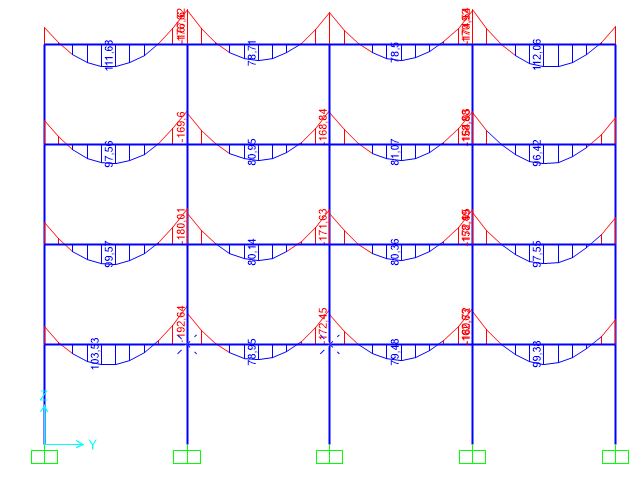

Diagramma del momento sulla travi(con vento)

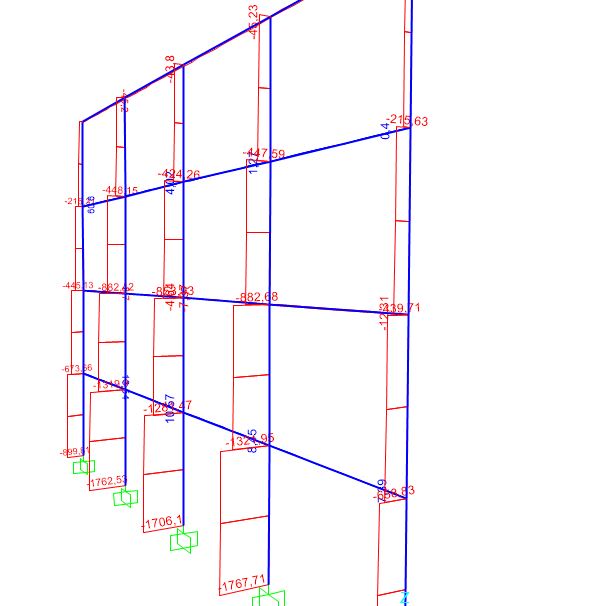
Diagramma della normale sui pilastri (con vento)

Diagrammi acciaio:

Schema strutturale

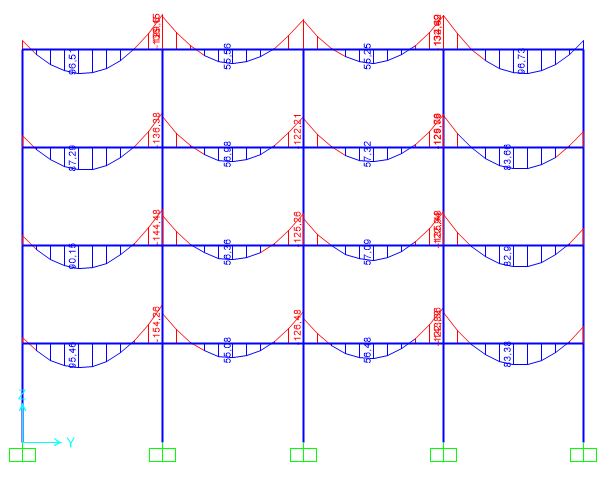Diagramma del momento sulle travi (con vento)

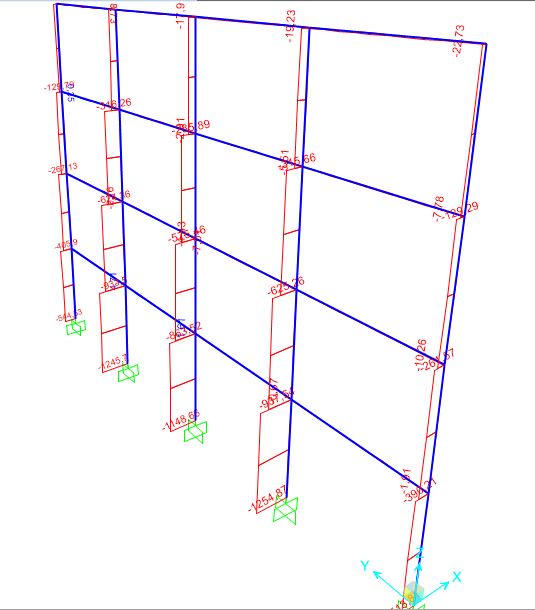
Diagramma della normale sui pilasti (con vento)

Diagrammi legno:

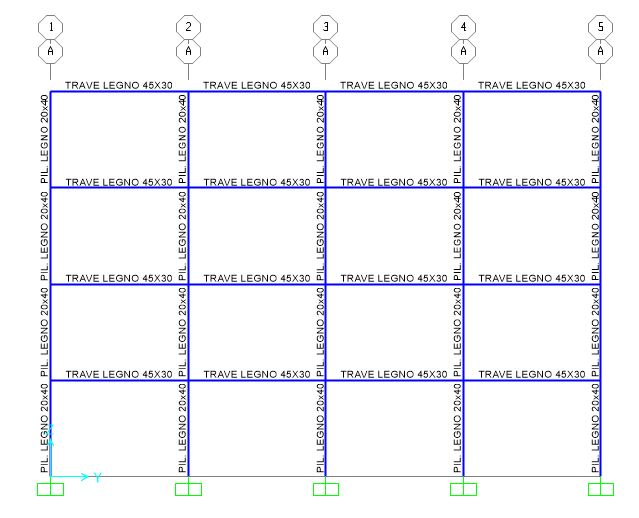Schema strutturale

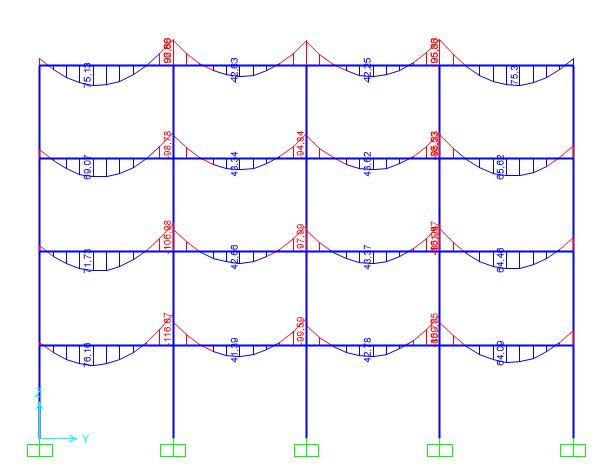Diagramma del momento sulle travi (con vento)

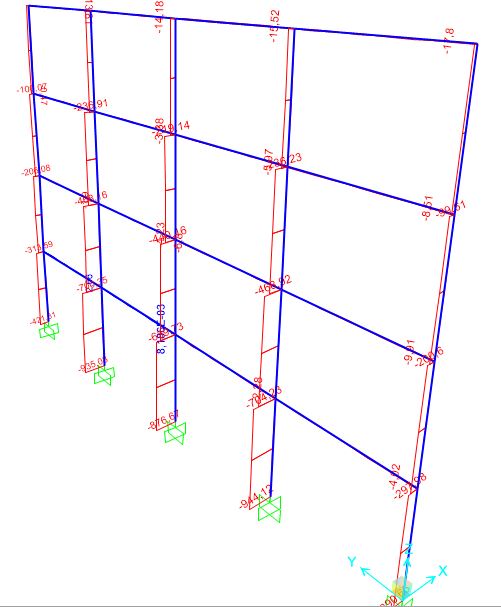
Diagramma della normale sui pilastri (con vento)

Le immagini precedenti mostrano la combinazione di carico che include anche la componente di carico orizzontale dovuta alla presenza del vento, che  aggiungiamo su SAP200 come carico orizzontale nella direzione Y (perpendicolare alla struttura) pari a:

F_vento = 0.70 ·i

Dove i è l’interasse sul prospetto minore (dimensione di una pressione kN/m, carico lineare).

Aggiungiamo alla relazione le sollecitazioni di momento e compressione per le tre tecnologie in assenza di vento. In questo caso i valori che otteniamo si avvicinano di più a quelli che risultano dal foglio di calcolo Excel, soprattutto per il legno e l’acciaio. Un'altra differenza è l'approssimazione che sul foglio di calcolo consideriamo per definire i vincoli che su SAP diventano più rigorosi.

Esercitazione eseguita con Veronica Stefanelli.