blog di emanuela.sforza

Per questa esercitazione dobbiamo trovare il centro delle rigidezze e verificare che sia coincidente o vicino al centro delle masse, così da evitare rotazioni della struttura in caso di sisma.

Abbiamo preso in considerazione un piano dell'edificio. Il telaio è in cemento armato, con una griglia strutturale di 6m per 5m.

Dopo aver disegnato la griglia possiamo inserire i setti (sempre in cemento armato) in cui andranno posizionati i corpi scala.

Poi assegnamo le sezioni alle travi ed ai pilastri, troviamo il centro delle masse e assegniamo la condizione di corpo rigido a tutti i punti che si trovano sulla quota delle travi (compreso il centro delle masse).

A questo punto avviamo l'analisi per ricavare il peso proprio della struttura, tramite le tabelle. Si moltiplica il peso per il coefficiente 0,2 (Roma è a basso rischio sismico).

 Assegniamo un carico concentrato del valore trovato in direzione X e poi in direzione Y e avviamo di nuovo l'analisi e verifichiamo che ci sia solo una traslazione e non una rotazione.

In conclusione il nostro centro delle masse coincide con il centro delle rigidezze.

Nella progettazione di una trave reticolare spaziale si inizia realizzando un modulo 3x3x3 che si ripete nelle direzioni X Y.

Successivamente si assegnano tutti i vincoli, i nodi sono delle cerniere interne che impediscono il passaggio del momento, assign > frame > release/partial fixity > nella finestra si selezionano le caselle start e end di moment 22 e moment 33, impostando come valore 0. 

Nei punti in cui la trave poggia sul pilastro inseriremo cerniere esterne. 

Poi si assegna la sezione in acciaio con profilato tubolare.

Il passo successivo è quello di stabilire i carichi che gravano su questa trave reticolare spaziale:

il carico dato dal solaio in acciaio è q=8,65 kN/m² 

l’area di un singolo piano è A=30*12=360 m², quindi ogni piano ha un carico totale qᵤ=8.65*360=3114 kN

l’edificio si eleva per cinque piani, q=5*3114=15570 kN

Suddividendo il carico totale sui nodi avremo una forza concentrata in ogni nodo di Q= 15570/55=283 kN.

Avviando l’analisi si otterrà la deformata della struttura.

Nell'analisi otterremo anche i valori di sforzo normale, che vengono estratti in una tabella Excel. 

 Nella tabella si nota come i valori del momento sono tutti uguali a 0.

Da questa tabella generale si estraggono i dati utili per il dimensionamento delle aste soggette a trazione e di quelle soggette a compressione, si dividono i valori di segno positivo (aste tese) da quelli di segno negativo (aste compresse).

Per il dimensionamento delle aste tese trovo Amin=N/fyd e scelgo un profilo con area maggiore.

Nel dimensionamento delle aste compresse oltre all’area minima bisogna tener conto sia dell’inerzia che del raggio d’inerzia per evitare fenomeni di instabilità.

Esercitazione 1

Nella prima esercitazione dobbiamo progettare e verificare un telaio in calcestruzzo armato,  in acciaio e in legno.

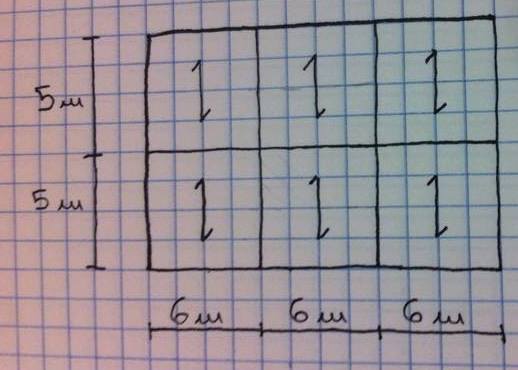
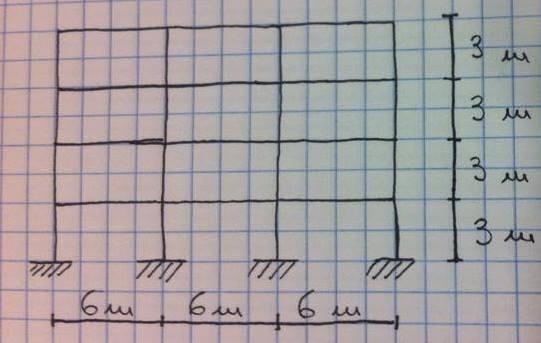
Calcestruzzo armato

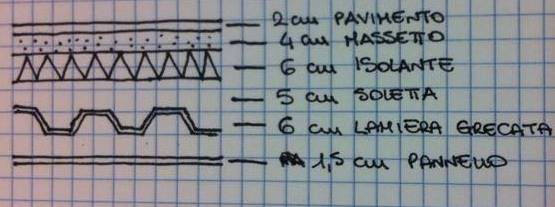
Occorre effettuare innanzitutto un'analisi dei carichi, calcolando i carichi del solaio qs (strutturale permanente), qp (portato) e qa (accidentale).

Attraverso la combinazione di carichi trovo il carico ultimo qu= (1,3*qs+1,5*qp+1,5*qa)*i

Per il progetto della trave ho innanzitutto il momento massimo Mmax=(ql^2)/8.

Scelgo fyk dell'acciaio delle armature e fck del calcestruzzo. Da queste mi ricavo le tensioni di progetto fyd e fcd. Ottengo poi l'altezza utile hu scegliendo una determinata base b. Aggiungo all'altezza utile la distanza δ, cioè la lunghezza dello spazio tra l'armatura e il bordo della sezione. Trovo l'altezza minima Hmin e la ingegnerizzo tenendo conto che per una buona resistenza a flessione l'altezza deve essere ben più grande della base.

Effettuo poi la verifica calcolando l'area della trave e il suo peso proprio, che aggiungo al carico ultimo. Ora ricalcolo il momento massimo e l'altezza minima. Se questa è minore dell'altezza di design allora è verificata.

A questo punto posso passare al progetto dei pilastri. Scelgo il pilastro più sollecitato del telaio. Calcolo la sua area di influenza, poi il peso delle travi e il carico ultimo del solaio che influisce sul pilastro. Trovo lo sforzo normale N e lo moltiplico per il numero di piani ottenendo Nmax

Poi scelgo fck da cui ricavo la tensione di progetto fcd. Mi calcolo l'area minima e trovo il valore minimo del raggio d'inerzia minimo ρ min. Ora posso ricavarmi la base minima b e l'altezza minima h. Ingegnerizzo entrambe le dimensioni, considerando che per i pilastri è ottimale una sezione quadrata.

Occorre ora verificare i pilastri. Calcolo l'area di design e il momento d'inerzia minimo. Poi mi ricavo il modulo di resistenza a flessione Wmax e ottengo infine il momento massimo Mmax. Da questo posso calcolarmi la tensione massima σmax. Se questa è inferiore a fcd trovata prima allora è verificato.

Acciaio

Effettuo l'analisi dei carichi come fatto per il calcestruzzo e trovo il momento massimo.

Scelgo fyk e ricavo la tensione di progetto fyd. A questo punto calcolo Wmin (modulo di resistenza a flessione). Una volta calcolato Wmin devo scegliere l'IPE che sui profilari ha un valore del modulo di resistenza a flessione maggiore di quello calcolato (IPE400).

Ora bisogna progettare i pilastri e anche qui eseguo gli stessi calcoli iniziali fatti anche per il calcestruzzo. Mi calcolo Nmax, scelgo fyk e trovo la tensione di progetto fyd. Calcolo l'area minima e poi il valore minimo del  raggio d'inerzia minimo. A questo punto trovo il momento d'inerzia minimo Imin, lo confronto con quelli nella tabella dei profilati metallici e scelgo l'HE con il momento d'inerzia più grande di quello calcolato (HEA260).

Legno

Anche in questo caso inizio effettuando l'analisi dei carichi e calcolando il momento massimo Mmax.

Scelgo fmk e kmod (0,7). Mi calcolo la tensione di progetto fd. Poi decido la base b e trovo l'altezza minima utilizzando la formula hmin= radq(Mmax/b)*radq(6/fd).

Ingegnerizzo anche qui l'altezza arrotondandola per eccesso e ottengo la sezione della trave.

Nel progettare il pilastro inizio sempre calcolandomi i carichi e Nmax. Scelgo fc0k e kmod e calcolo la tensione di progetto fc0d. Mi calcolo l'area minima, la snellezza e il valore minimo del raggio d'inerzia minimo. Dopodichè mi trovo la base minima bmin e l'altezza minima hmin. Le ingegnerizzo e calcolo l'area e il momento di inerzia minimo.