1. ANALISI DEI CARICHI
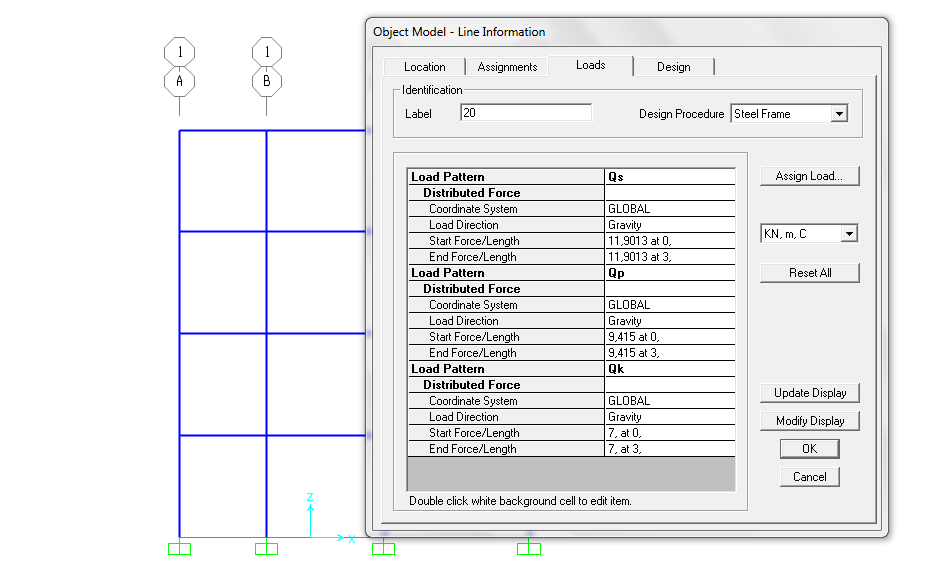
1.1 CARICO DEL SOLAIO
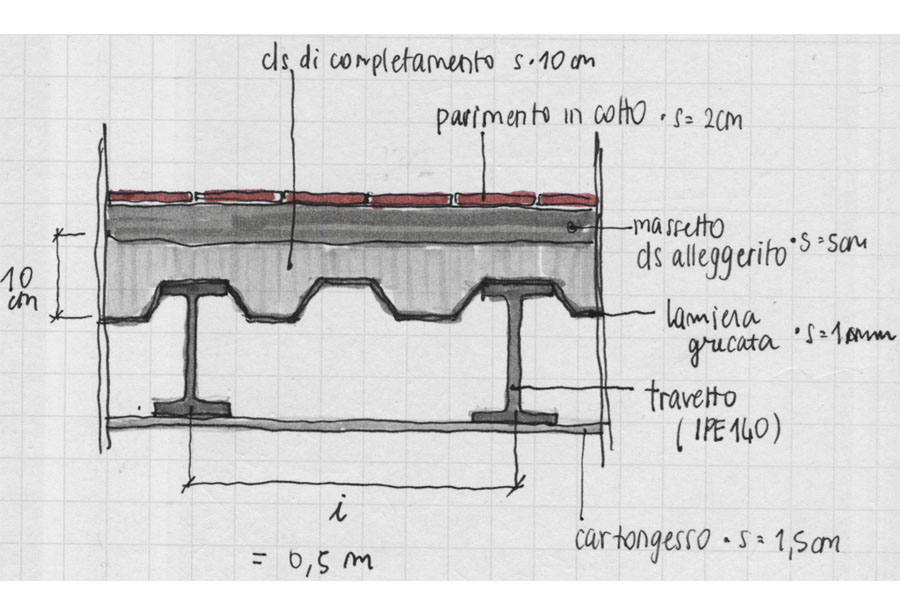
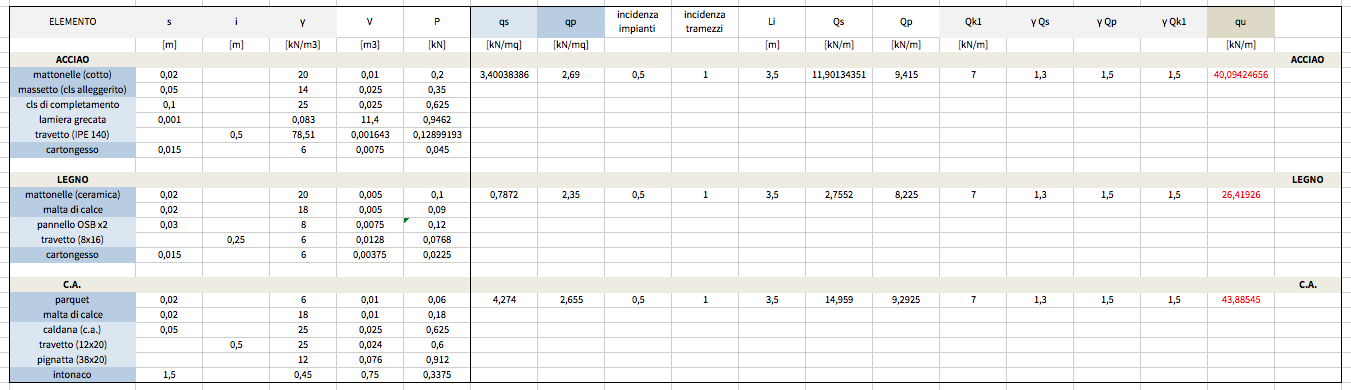
Individuo i valori del peso specifico di ogni materiale (gamma) à [kN/m3]
Calcolo il peso al mq degli elementi, suddividendo tra carico strutturale (qs) e carico permanente portato (qp)
qx [kN/mq] = [(V [m3] / 1 mq) * gamma + ... ] * (1/i)
in cui V= volume elemento calcolato rispetto all’interasse (in questo caso 0,5 m) = spessore*0,5*1m; gamma= peso specifico; i= interasse.
Per il calcolo del cls di completamento ho arrotondato considerando lo spessore pari a 5 cm.
Per il travetto (IPE 140) ho preso dal sagomario il peso in kg/m
Peso IPE140 = 12,9 Kg/m *1m Volume IPE140 = area*1m =0,001643 [m3]
Peso specifico = peso / volume = 12,9 Kg / 0,001643 m3 = 129*10^(-3) [kN] /0,001643 [m3] =78,51 kN/m3
Calcolo i carichi al metro lineare
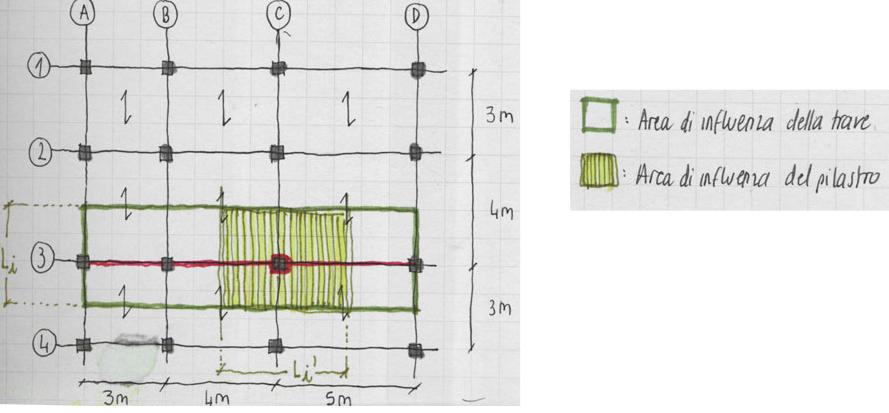
Qs [kN/m] = qs*Li
Qp [kN/m] =(qp + incidenza tramezzi + incidenza impianti )*Li
in cui Li= lunghezza dell’area di influenza (indicata in figura); varia a seconda della trave considerata
incidenza tramezzi = 1 kN/mq; incidenza impianti= 0,5 kN/mq
Calcolo la combinazione di carico frequente per un edificio di civile abitazione
qu [kN/m] = Qs*gamma qs+Qp*gamma qp+Qk1*gamma qk1+ Qk2*gamma qk2* psi 02 + ...
in cui Qk= (carico accidentale da NTC, per civile abitazione=2kN/mq àsto considerando il carico di persone come carico accidentale dominante)

1.2 PESO PROPRIO della TRAVE
* da aggiungere dopo averla dimensionata ma prima di dimensionare il pilastro
2. PREDIMENSIONAMENTO DELLA TRAVE PRINCIPALE Più SOLLECITATA (trave 2) à flessione pura S450
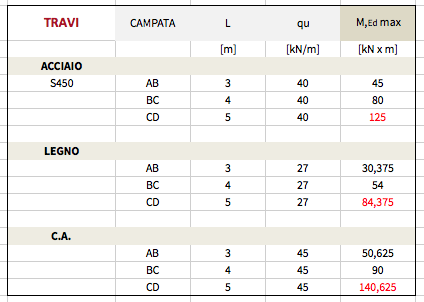
Calcolo delle sollecitazioni in mezzeria
(tralascio in questo momento il contributo del taglio, che però potrebbe contribuire a ridurre la resistenza della trave influenzando il momento!!)
Mmax [kN*m] = qu*(L^2)/8
In cui Mmax= momento in mezzeria e L= campata CD
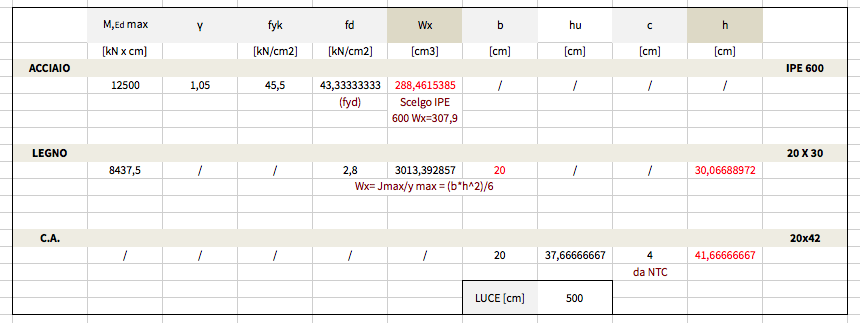
Calcolo il modulo di resistenza a flessione (hp. sezione in classe 1: no instabilità flesso-torsionale)
Dalla formula di Navier so che sigma(y) = (Mx / Ix)* y à sigma max= (Mx/Ix)*ymax à Ix/ymax = Wx
Wx [cm^3] = Mmax/sigma max = Mmax/ fyd
In cui sigma max= fyd per imposizione di progetto; fyd= resistenza di progetto = fyk/gamma à gamma =1,05 coef. di sicurezza: riduce la resistenza caratteristica del materiale (fyk).
Arrotondo per eccesso e scelgo dal sagomario una trave con Wx >= a quello ottenuto.
Scelgo trave IPE 600
3. PREDIMENSIONAMENTO PILASTRO Più SOLLECITATO (pilastro C3) à presso-flessione HEA
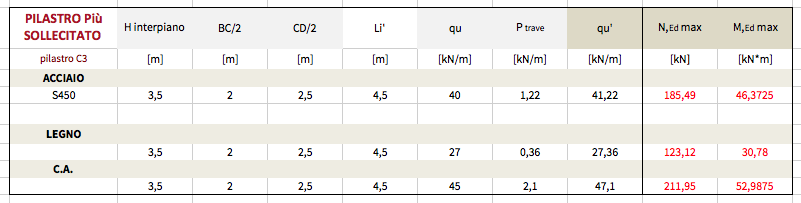
Calcolo il peso proprio della trave e lo sommo a qu à ottengo qu’
Calcolo le sollecitazioni all’incastro
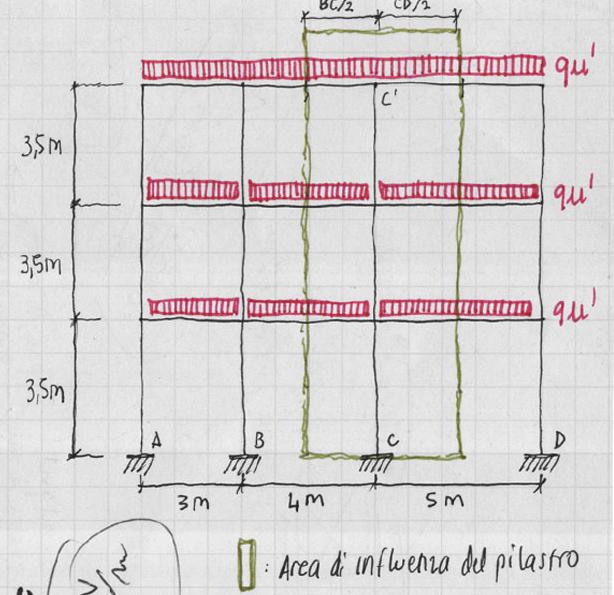
Mmax [kN*m] = P1*(a/2) – P2* (b/2)
N max [kN] = qu’ * Li’
In cui Li’= lunghezza di influenza del pilastro C3; a= campata CD/2; b=campata BC/2
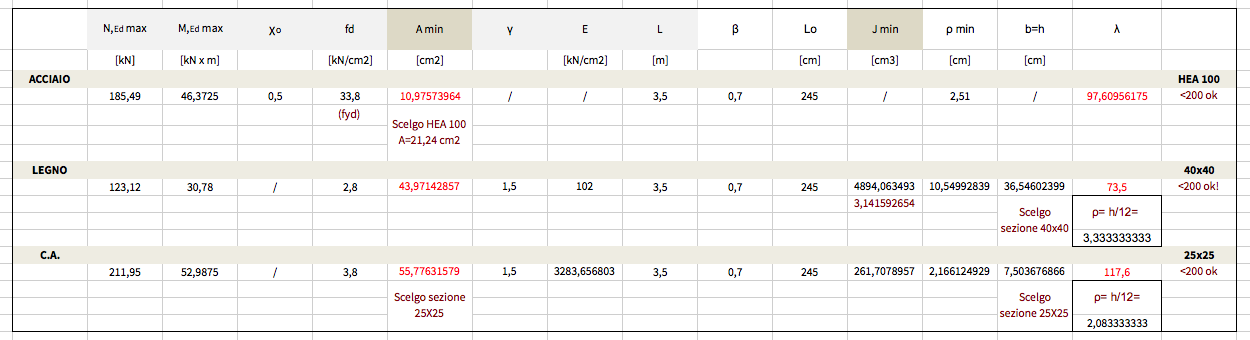
Calcolo l’area minima
A minima [cm2] = Ned/(fyd*Xo)
In cui Xo= X di primo tentativo <1 à coef. che tiene conto preventivamente della possibile insorgenza di instabilità.
Scelgo dal catalogo un profilato con sezione di area >= a quella ottenuta
Scelgo HEA100
3.1 VERIFICO LA SNELLEZZA DEL PILASTRO
Ottengo il ro min dai dati nel sagomario
ro minore= 2,51 cm
lambda [adim] = lo/ro min = 400*0,7/2,51=111,55 ok se <=200
in cui lo=L*beta con beta=0,7 (varia a seconda dei vincoli agli estremi)
4. VERIFICA SU SAP
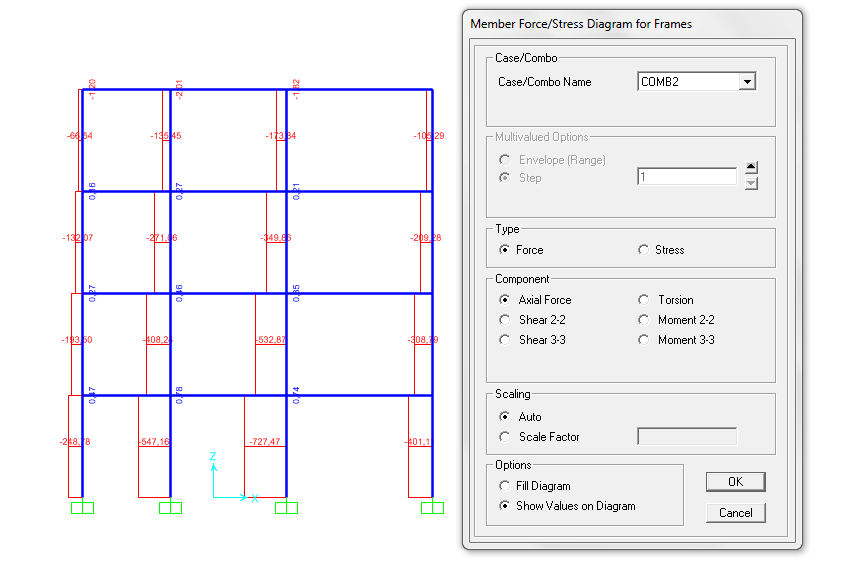
! Dall’analisi su SAP è evidente come il progetto del pilastro non sia adatto a sostenere il carico che arriva al piano terra, infatti nel predimensionamento ho considerato solo il peso di un solaio invece di moltiplicare il peso qu’ per il numero di piani del telaio E aggiungere inoltre il peso proprio del pilastro!!
Questo stesso errore/incompiutezza è ripetuto per tutti i telai (c.a. e legno); è necessario quindi riprogettare il pilastro tenendo conto dell’aumento dei carichi mano a mano che si scende verso le fondazioni.
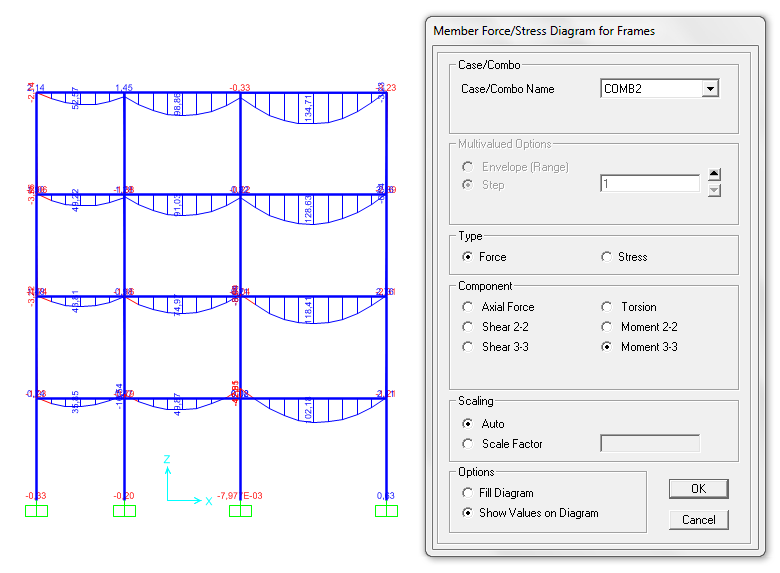
Oltre a questo ho notato che il progetto del pilastro e della trave che ho eseguito con EXCEL (che sono quindi il pilastro e la trave dell’ultimo piano) sono da rivedere, essendo le sollecitazioni di SAP leggermente maggiori di quelle ottenute su EXCEL.
Commenti recenti