blog di carlotta.avenali1

 

L'esercitazione è svolta in coppia con Fabrizio Pontico.

 

Lo scopo dell’esercitazione è quello di verificare che l’impalcato resista alle forze sismiche:tali forze agiscono nel centro di massa,quindi è necessario che il centro di massa coincida il più possibile con il centro delle rigidezze della struttura. Una struttura può essere resa più rigida attraverso l’utilizzo di controventi,che sono elementi verticali collegati orizzontalmente che portano il carico fino a terra,che possono essere per esempio i vani ascensori,le scale o anche un semplice telaio.

Il nostro impalcato è formato da una struttura semplice a telaio,formato da travi e pilastri. Per motivi di progetto e di struttura abbiamo deciso già dalle prime fasi di considerare i blocchi scale e gli ascensori come una struttura autonoma,collegata al telaio attraverso un giunto strutturale.

L’impalcato ha una struttura in cemento armato con classe di resistenza C40/50 formato da travi 35x50 cm e pilastri 50x50 cm.

Dopo aver disegnato la struttura su Sap passiamo ad assegnare ai vicoli esterni il vincolo di incastro. Si disegna inoltre il centro di massa,corrispondente al centro geometrico della struttura partendo dall’intersezione delle due diagonali.

Selezionando il punto del centro di massa e tutti i punti nel piano xy alla stessa quota delle travi e’ possibile assegnare la condizione di corpo rigido: in questo modo tutti i punti fanno parte dell’impalcato e non possono esserci spostamenti o rotazioni relative. 

Per verificare che il centro di massa e quello di rigidezza coincidano prendiamo in considerazioni le due peggiori combinazioni di casi,ovvero quando la forza sismica è applicata lungo una direzione. Andiamo ad calcolare prima il peso specifico della struttura, imponendo una combinazioni di carico data esclusivamente dal peso proprio della struttura, poi importiamo la tabella su excell e sommando i valori delle reazioni  vincolari verticali otteniamo il peso proprio che è 1909,83 kN. Moltiplichiamo questo valore per 0,2,cioè il coefficiente di riferimento per le zone a basso rischio sisma come Roma, e otteniamo così il valore del carico sismico di 381,94 kN.

A questo punto è possibile applicare il carico sismico come un carico concentrato orizzontale prima nella direzione X e poi nella direzione Y per verificare che la deformata non sia una rotazione ma una traslazione (in entrambe le direzioni).

Da i risultati dell’analisi è evidente che non c’è nessuna rotazione ma due traslazioni,sull’asse X quando la forza è applicata lungo questa direzione, e sull’asse Y quando la forza è lungo quest’altra direzione, quindi è possibile dire che il centro di massa coincida con il centro delle rigidezze,pertanto non è necessario l’aggiunta di controventamenti come scale e ascensori.

Esercitazione di Avenali Carlotta e Pontico Fabrizio.

Il graticcio che andremo a studiare è in cemento armato e copre un’area di 12 m x 35 m,al di sopra ci sono tre piani ed è sorretto da una serie di setti sempre in cemento armato. La disposizione dei setti è casuale,perché la nostra intenzione è proprio quella di creare una serie di pilastri (o nel nostro caso setti) randomici, che non diano l’idea di una maglia strutturale rigida al piano terra.

La maglia del graticcio è di 1.5 m x 1.5 m e le travi che lo compongono hanno la stessa sezione in entrambe le direzioni poiché in questa tipologia strutturale non c’è gerarchia.

Prima di inserire la struttura su SAP è stata creata una combinazione di carico in cui sono stati moltiplicati i valori dei carichi strutturali,dei carichi permanenti e accidentali per i loro coefficienti di sicurezza

Qu=(qs*1.3+qp*1.5+qa*1.5)= 10.34 kN/m2

Ora moltiplichiamo il carico di un solo piano per il numero di piani che abbiamo,cioè 3 e risulta un Qu=31.02 kN/m2

Successivamente e’ stato assegnato il carico alle travi dividendolo per le due direzioni: in questo modo il carico e’ stato moltiplicato per l’area di influenza delle travi centrali pari 41.36 kN/m (con area di influenza 0,75 m) e un carico Qu=82.72 kN/m per le travi di bordo (con area di influenza 0,375 m).

A questo punto abbiamo importato il graticcio in SAP facendo attenzione che i singoli elementi fossero divisi  e abbiamo assegnato i valori di incastro in prossimità dei nostri setti

 

E’ stata ipotizzata una sezione di 30 cm x 140 cm con la classe del cemento di C30

Avviando l’analisi dei carichi è stato possibile osservare la deformata e i momenti flettenti

Importando i dati su un foglio Excell è stato possibile individuare il momento flettente massimo,pari a 208.18 kN*m e attraverso un altro foglio Excell verificare che la sezione ipotizzata fosse corretta. Il risultato,mantenendo la base pari a 30 cm è di un’altezza pari a 66.8 cm quindi la nostra sezione è verificata.

Successivamente siamo passati a verificare la deformabilità,in particolar modo dell’abbassamento verticale del graticcio,che risulta essere 0.00006 m nell’estremo in alto a sinistra.

Sappiamo deve essere inferiore a 1/200 della luce che in questo caso è pari a 3.60 m,quindi 0.018 quindi anche in questo caso è verificato.

 

Per il progetto e verifica di una trave abbiamo disegnato un telaio (struttura composta da un sistema di elementi verticali, pilastri, ed elementi orizzontali, travi) e verrà progettata proprio la trave maggiormente sollecitata con tre diverse tipologie costruttive differenti,tra cui cemento armato,acciaio e legno.

 

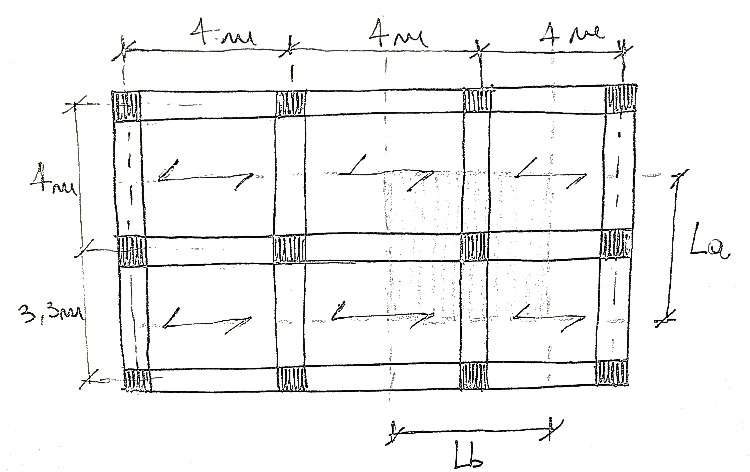
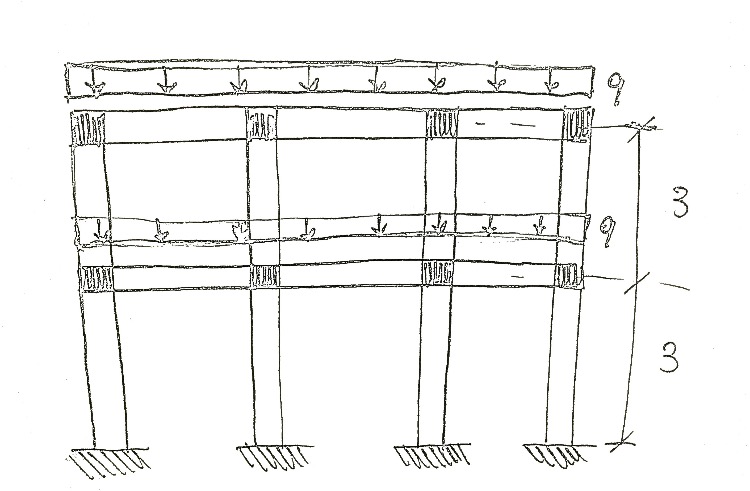
L’area di influenza delle travi è 14,6 m2.

Dimensioneremo la trave principale che risente di una maggiore area di influenza di carico.

Passiamo ora a fare l’analisi dei carichi del solaio:

 

Solaio in cemento armato:

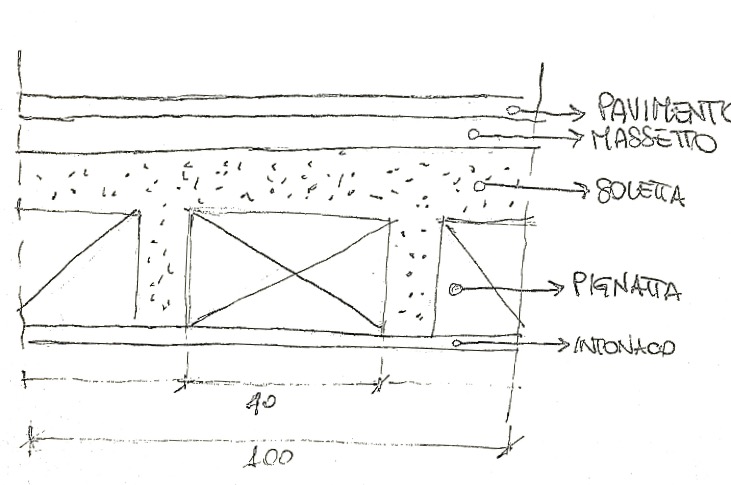
Qs:Carico strutturale permanente:

Travetti=0.16(m)*0.1*2(m)*25(kN/m3)=0.8(kN/m2)

Soletta=0.04(m)*1(m)*25(kN/m3)=1(kN/m2)

Pignatta=0.16(m)*0.4*2(m)*5.5(kN/m3)=0.7(Kn/m2)

Qs tot=2.5(kN/m2)

Qp:Carico non strutturale permanente:

Intonaco=0.015(m)*1(m)*20(kN/m3)=0.3(kN/m2)

Massetto=0.04(m)*1(m)*19(kN/m3)=0.76(kN/m2)

Pavimento in gress=0.02(m)*1(m)*1(m)=0.4(kN/m2)

Qp tot=2.73(kN/m2)

Qa:Carico variabile

Qa=2(kN/m2) per un ambiente ad uso residenziale

Qu:Carico ultimo

Qu:Qs*1.3+Qp*1.5+Qa*1.5=10.34(kN/m2)

Per trovare il carico ultimo al metro lineare basta dividerlo per la luce quindi diventa Qu*4=41.38(kN/m)

Possiamo fare riferimento al modello di trave doppiamente appoggiata e sappiamo che il suo momento flettente massimo,vale in mezzeria ql^2/8 quindi ci viene un Mmax=82.76(kN*m)

I dati mancanti sono il valore della resistenza caratterista del calcestruzzo e la resistenza di progetto del calcestruzzo e dell’acciaio.

La resistenza fcd è data da fck*0.8/1.5 mentre fck è il valore della classe di resistenza del calcestruzzo che desideriamo scegliere.

Sapendo i moduli elastici dei due materiali pari a Es=210000(N/mm2) e Ec=22000(N/mm2) possiamo ricavarci l’altezza minima della sezione partendo dalla scelta arbitraria della base.

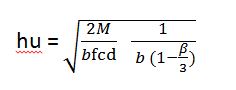
Inserendo i dati del carico risulta necessaria una trave con altezza utile alte 42,14 cm

considerando un copriferro di 5 cm per coprire le barre d'acciaio risulta necessaria una trave principale alta 47,14 cm.
Per una facilità di realizzazione della trave, la sezione viene ingegnerizzata, quindi verrà utilizzata una trave con un altezza di 55 cm.

 

Solaio in acciaio:

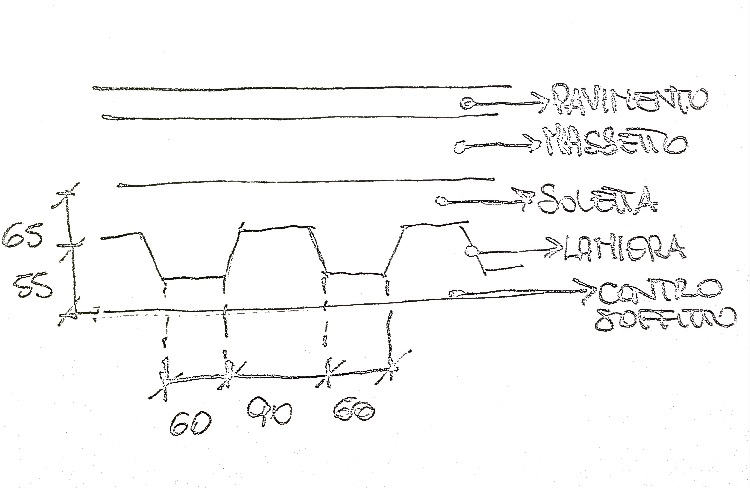
Qs:Carichi strutturali permanenti

Lamiera:tipo A55/P600 *0.8(m)=0.11(kN/m2)

Soletta:0.065(m)+0.55/2(m)*25=2.32(kN/m2)

Qs tot:2.43(kN/m2)

Qp:Carico permanente non strutturale

Massetto:0.1(m)*0.1(m)*20(kN/m3)=2(kN/m2)

Pavimento in gress: 0.02(m)*1(m)*1(m)=0.4(kN/m2)

Qp tot:4.16(kN/m2)

Qa:Carico variabile

Qa=2(Kn/m2) per un ambiente ad uso residenziale

Qu:Carico ultimo

Qu:Qs*1.3+Qp*1.5+Qa*1.5=12.39(kN/m2)

Per trovare il carico ultimo al metro lineare basta dividerlo per la luce quindi diventa Qu*4=49.59(kN/m)

 

Una volta scelto il tipo di acciaio che vogliamo utilizzare basta trovare la resistenza di progetto pari a Fyd=Fyk/1.05

Il momento flettente massimo è in mezzeria e vale ql^2/8 quindi 99.19(kN*m).

Ora per progettare la trave abbiamo bisogno del modulo di resistenza plastico,cioè il rapporto tra il momento massimo e la sua resistenza di progetto Wpl=Mmax/Fyd=320.46(cm3)

Ora basterà prendere un profilario con le sezioni IPE e scegliere la trave con un modulo di resistenza maggiore di quello calcolato,per essere sicuri di progettare in sicurezza e in modo che il momento flettente di calcolo sia minore di quello resistente. Scegliamo dunque un IPE 240

 

Solaio in legno:

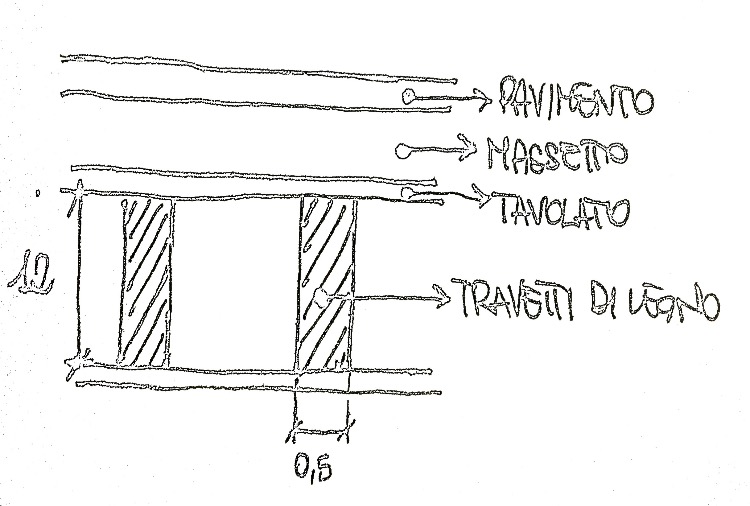
Qs:Carichi strutturali permanenti

Travetti in legno=0.1(m)* 0.2(m)* 1(m)*1.80(kN/m3)=0,078(kN/m2)

Tavolato in legno=1(m)* 1(m) *0.03(m)*7.2(kN/m3)=0.216( kN/m3)

Qs tot:0.38(kN/m2)

Qp:Carichi permanenti non strutturali

Isolante in pannelli di Fibra di Legno=1(m)* 1(m)* 0.04(m)=0.056 (kN/m2)

Massetto=1(m)*1(m)*04(m)*18 (Kn/m3) = 0.72 (kN/m2)

Pavimento in parquet=1(m) *1(m)*0.02(m)*7.2 (Kn/m3) = 0.144(kN/m2)

Qp tot:2.26(kN/m2)

Qa:Carico variabile

Qa=2(Kn/m2) per un ambiente ad uso residenziale

Qu:Carico ultimo

Qu:Qs*1.3+Qp*1.5+Qa*1.5=6.88 (kN/m2)

Per trovare il carico ultimo al metro lineare basta dividerlo per la luce quindi diventa Qu:27.55(kN/m)

Il momento flettente massimo è in mezzeria e vale ql^2/8 quindi 55.11(kN*m).

Possiamo scegliere ora la classe di resistenza del legno,pari a 34(N/mm2) e calcolarci la resistenza di progetto data dalla formula 

Con γm=1.45 e kmod=0.8 Fd risulta quindi 17.65(N/mm2)

Per poter determinare la sezione dobbiamo prima trovare il modulo di resistenza dato dal rapporto tra il Mmax e la resistenza di progetto Fd.

Una volta trovato il modulo di resistenza possiamo scegliere arbitrariamente una delle due lunghezze della sezione mancanti,in questo caso scegliamo la base pari a 16 cm e attraverso la formula 

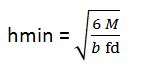
Possiamo determinare l’altezza utile pari a 34.21(cm) quindi scegliamo un altezza di 35(cm).

 

 

Passiamo alla progettazione del pilastro più sollecitato,sempre nelle tre diverse tipologie.

Cemento armato:

Come prima cosa dobbiamo determinare lo sforzo normale massimo che sollecita il pilastro.

Per trovare lo sforzo normale abbiamo bisogno del carico ultimo (dato dalla combinazione dei carichi precedente),il numero dei piani e l’area di influenza del pilastro e il peso della trave.

Ora avendo lo sforzo massimo possiamo determinare l’Area minima della sezione facendo il rapporto dello sforzo normale N e Fcd,pari a 264.30(cm2).

Con la formulazione del carico critico euleriano sappiamo che lo sforzo normale che manda in crisi il pilastro per il fenomeno di instabilità è ( π^2*E*Imin)/Lo^2 .

 

Da qui devo ricavarmi la Lo,cioè la lunghezza libera di inflessione del pilastro data L*β (Coefficiente di vincolo)

Ora occorre trovare λ cioè la snellezza  critica data dalla formula ((π^2*E)/Fcd)^0.5  cioè 123.44

Possiamo ricavarci dunque il raggio giratore d’inerzia cioè Lo/ λ pari a 2.43(cm).

Avendo una sezione rettangolare sappiamo che il momento d’inerzia è pari a B*H^3/12 quindi attraverso il raggio giratore d’inerzia possiamo ricavarci con la formula inversa I=A*ρ^2 la base e l’altezza della sezione.

Si sceglie così una sezione di  35 * 35 (cm)

 

Acciaio:

Partendo sempre dal calcolo dello sforzo normale come nel caso del cemento armato possiamo determinare lo sforzo normale agente sul pilastro più sollecitato e partire con il progetto del pilastro.

 Avendo determinato la sezione e scelto quindi un HEA 140 dobbiamo verificare inoltre che la snellezza critica sia minore della snellezza del pilastro,perché nell’acciaio non è solo lo sforzo normale che manda in crisi la sezione ma anche la snellezza,quindi possiamo determinare la snellezza con λ=Lo*ρ  che risulta pari a 85.22 e verificare che sia effettivamente minore di  λc cioè 96.23

 

Legno:

 Lo stesso procedimento è stato effettuato per la tipologia costruttiva in legno