blog di Lucia.Pietrofresa

AUTOCAD:

1) Con il nuovo layer "ASTE" si disegna il modulo di partenza (2x2) della struttura

2) Orbitando, si passa da una visualizzazione 2d a una 3d

3) Con il comando Array si duplica il modulo 2x2 e si costruisce la struttura completa

4) Si esplode tutto il disegno e lo si salva nel formato dxf 2000

SAP2000:

1) Si importa nel programma il disegno Autocad e alla voce "Telai" si seleziona il layer "ASTE" realizzato in precedenza

2) Si inseriscono i vincoli esterni (4 cerniere ai 4 vertici della base della struttura)

3) Si impone a tutte le aste la condizioni di momenti nulli sia all'inizio che alla fine

4) Dopo aver definito il materiale della struttura (acciaio) e le dimensioni della sezione (tubo di diametro 6 e spessore 0.25), si assegnano dei carichi concentrati di 40 KN

5) Infine, avviando il procedimento di calcolo, si ottengono le reazioni vincolari, il diagramma dello sforzo normale e il grafico della deformata

Reazioni

Diagramma Sforzo Normale

Deformata

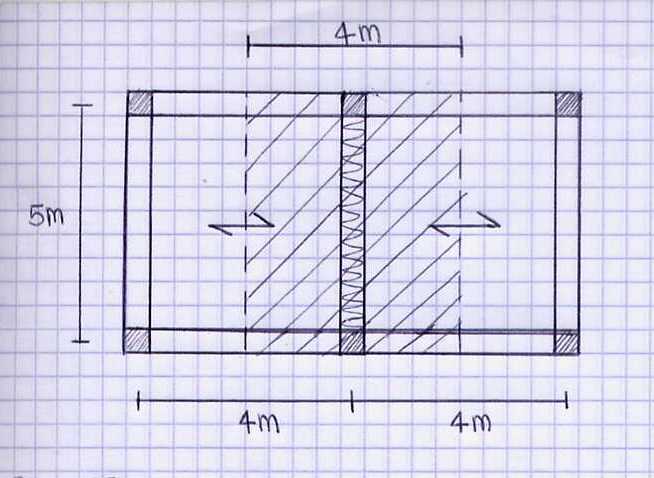
- DIMENSIONI SOLAIO:

interasse = 4m

luce = 5m

area d'influenza = 20mq

-CARICO ACCIDENTALE (qa)

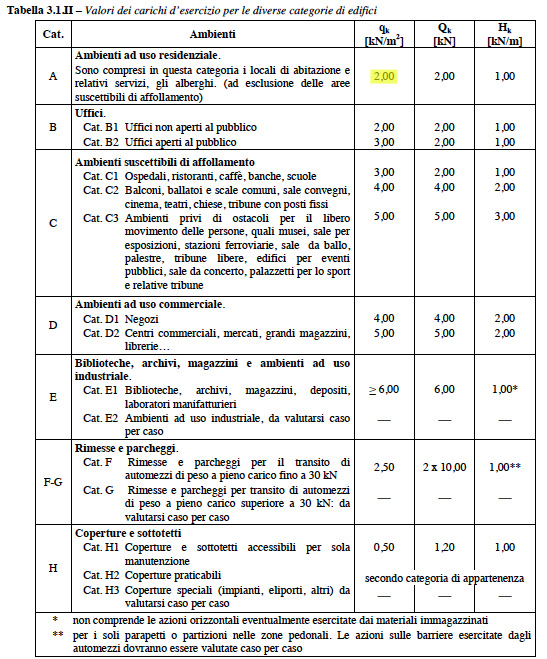
Ipotizzo che l'impalcato fa parte di un edificio residenziale. Osservando la seguente tabella, ricavo il valore del carico accidentale (qa = 2,00 KN/mq).

1) ACCIAIO

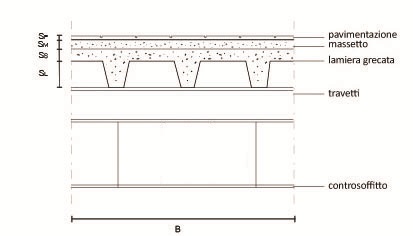
SP = 0,01 m

SM = 0,04 m

SS = 0,04 m

SL = 0,06 m

B = 1 m

- CARICO STRUTTURALE (qs)

soletta = ps*SS+ps*SL*0,5 = 25KN/mc*0,04m+25KN/mc*0,06m*0,5 = 1,75 KN/mq

lamiera grecata A55P600 = 1,15 KN/mq

travetti IPE160 = ps/B = 0,158KN/m/1m = 0,158 KN/mq

qs = soletta+lamiera+travetti = 3,058 KN/mq

- CARICO PERMANENTE NON STRUTTURALE (qp)

massetto = ps*SM = 18KN/mc*0,04m = 0,72 KN/mq

pavimento in ceramica = ps*SP = 40KN/mc*0,01m = 0,4 KN/mq

tramezzi = 1 KN/mq

impianti = 0,5 KN/mq

intonaco = ps*Si = 20KN/mc*0,02m = 0,4 KN/mq

controsoffitto in cartongesso = ps*SC = 0,08KN/mc*0,0125m = 0,1 KN/mq

qp = massetto+pavimento+tramezzi+impianti+intonaco+controsoffitto = 3,12 KN/mq

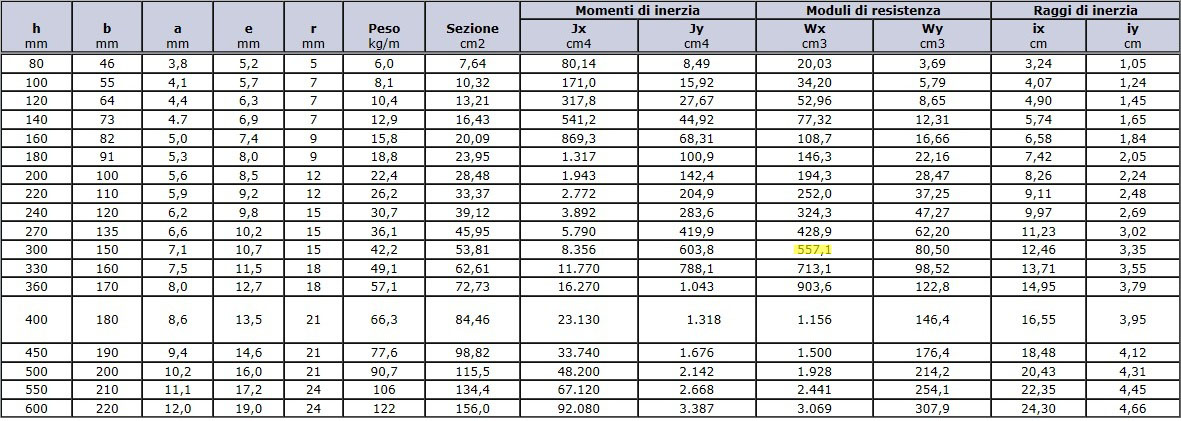
In base al valore del modulo di resistenza elastico (Wx) ottenuto nella tabella Exel, scelgo il profilato IPE300 dal sagomario:

2) LEGNO

SP = 0,01 m

SM = 0,04 m

ST = 0,02 m

B = 0,5 m

- CARICO STRUTTURALE (qs)

tavolato in rovere = ps*ST = 8KN/mc*0,02m = 0,16 KN/mq

travetto in rovere (9x10) = ps*Area/B = 8KN/mc*0,09m*0,10m/0,5m = 0,144 KN/mq

qs = tavolato+travetto = 0,304 KN/mq

- CARICO PERMANENTE NON STRUTTURALE (qp)

massetto = ps*SM = 18KN/mc*0,04m = 0,72 KN/mq

pavimento in ceramica = ps*SP = 40KN/mc*0,01m = 0,4 KN/mq

impianti = 0,5 KN/mq

tramezzi = 1 KN/mq

qp = massetto+pavimento+impianti+tramezzi = 2,62 KN/mq

3) CEMENTO ARMATO

SP = 0,01m

SM = 0,04m

SS = 0,04m

SL = 0,16m

Si = 0,02m

bt = 0,10m

bl = 0,40m

B = 1m

- CARICO STRUTTURALE (qs)

soletta = ps*SS = 25KN/mc*0,04m = 1KN/mq

travetto = ps*bt*SL*2/B = 25KN/mc*0,10m*0,16m*2/1m = 0,8 KN/mq

laterizi = ps*bl*SL*2/B = 8KN/mc*0,40m*0,16m*2/1m = 1,024 KN/mq

qs = soletta+travetto+laterizi = 2,824 KN/mq

- CARICO PERMANENTE NON STRUTTURALE (qp)

massetto = ps*SM = 18KN/mc*0,04m = 0,72 KN/mq

pavimento in ceramica = ps*SP = 40KN/mc*0,01m = 0,4 KN/mq

impianti = 0,5 KN/mq

tramezzi = 1 KN/mq

intonaco = ps*Si = 20KN/mc*0,02m = 0,4 KN/mq

qp = massetto+pavimento+impianti+tramezzi+intonaco = 3,02 KN/mq

1) Verifica dell'isostaticità

Affinchè una struttura reticolare sia isostatica, la somma dei vincoli esterni e del numero delle aste (condizioni di vincolo) deve essere uguale al numero dei nodi moltiplicati per due (gradi di libertà).

Ve + a = 2 n

2A + 1H + 11 = 2 * 7

14 = 14   (isostatica)

2) Equilibrio per Vincoli Esterni

La risultante delle due forze applicate è pari a 20KN e la sua retta d'azione incontra quella della reazione del carrello e quella della reazione della cerniera esterna in un punto; ciò vuol dire che la struttura è in equilibrio. Con il poligono delle forze otteniamo il verso delle reazioni dei vincoli esterni. Inoltre la reazione della cerniera esterna (RA) avrà una componente orizzontale (RuA) ed una verticale (RvA).

Poligono delle Forze

Componenti di RA

Riepilogo sulla Struttura

Risolvendo le equazioni di equilibrio otteniamo i valori delle reazioni incognite.

∑Fx=0       RuA-RH=0        RuA=RH

∑Fy=0       RvA-10KN-10KN=0      RvA=20KN

∑MA=0     -10KN*1-10KN*2+RH*1=0       RH=30KN

3) Metodo dei Nodi

Per conoscere il comportamento delle aste si utilizza il metodo dei nodi: si isola un nodo della struttura alla volta e poi si calcola il valore dello sforzo assiale di ogni asta, risolvendo le equazioni di equilibrio alla traslazione verticale e orizzontale.

∑Fx=0      NBC=0   (asta scarica)

∑Fy=0      NAB=0   (asta scarica)

∑Fx=0      30KN+NAD+NAC√2/2=0      NAD=-10KN   (asta compressa)

∑Fy=0      20KN+NAC√2/2=0       NAC=-20KN√2       (asta compressa)

∑Fx=0      10KN+NDG=0       NDG=-10KN       (asta compressa)

∑Fy=0      NCD=0      (asta scarica)

∑Fx=0      NCE+NCG√2/2+20√2KN*√2/2=0      NCE=-30KN      (asta compressa)

∑Fy=0      -10KN+20KN-NCG√2/2=0       NCG=10KN√2       (asta tesa)

∑Fx=0      30KN+NEH=0     NEH=-30KN     (asta compressa)

∑Fy=0      -10KN-NEG=0     NEG=-10KN     (asta compressa)

∑Fx=0      -NGH√2/2=0       NGH=0       (asta scarica)

4) Diagramma dello Sforzo Normale

Quando le strutture reticolari sono caricate solo sui nodi, le aste sono sollecitate solo a sforzo normale. Dove lo sforzo normale è positivo, l'asta lavora a trazione e viene chiamata tirante, mentre dove è negativo l'asta lavora a compressione e viene denominata puntone.

5) SAP 2000

Per avere conferma dei risultati ottenuti, risolviamo l'intera struttura con il programma SAP 2000.

Grafico della Deformata

Diagramma dello Sforzo Normale

1) Verifica dell'isostaticità

Affinchè una struttura reticolare sia isostatica, la somma dei vincoli esterni e del numero delle aste (condizioni di vincolo) deve essere uguale al numero dei nodi moltiplicati per due (gradi di libertà)

Ve + a = 2 n

3 + 11 = 2 * 7

14 = 14    (isostatica)

2) Equilibrio per Vincoli Esterni

La risultante delle tre forze applicate si trova proprio sull'asse di simmetria ed è pari a 60 KN. Le reazioni dei vincoli esterni saranno parallele alla risultante, di verso opposto e di valore dimezzato (30 KN).

3) Metodo di Ritter

Siccome la struttura è simmetrica se ne risolve solo una metà. Per conoscere il comportamento delle aste si utilizza il metodo di Ritter: si effettuano tre sezioni sulla struttura, tagliando tre aste non convergenti nello stesso punto, e successivamente si calcolano gli sforzi assiali delle aste attraverso l'equazione di equilibrio al momento del nodo preso in considerazione.

∑MB=0     -30KN*2+NAC*2=0     NAC=30KN   (asta tesa)

∑MC=0    -30KN*4-NAB2√2=0    NAB=-30√2KN   (asta compressa)

∑MC=0    -30KN*4+20KN*2-NBD*2=0      NBD=-40KN   (asta compressa)

∑MD=0   -30KN*6+20KN*4+30KN*2+NBC2√2=0     NBC=10√2KN   (asta tesa)

∑MD=0   -30KN*6+20KN*4+NCE*2=0   NCE=50KN   (asta tesa)

∑ME=0   -30KN*8+20KN*6+40KN*2-NCD2√2=0        NCD=-10√2KN    (asta compressa)

4) Diagramma dello Sforzo Normale

Quando le strutture reticolari sono caricate solo sui nodi, le aste sono sollecitate solo a sforzo normale. Dove lo sforzo normale è positivo, l'asta lavora a trazione e viene chiamata tirante, mentre dove è negativo l'asta lavora a compressione e viene denominata puntone.

5) SAP 2000

Per avere conferma dei risultati ottenuti, risolviamo l'intera struttura con il programma SAP 2000.

Grafico Deformata

Diagramma dello Sforzo Normale