STRUTTURA RETICOLARE SIMMETRICA

1) Verifica dell'isostaticità

Affinchè una struttura reticolare sia isostatica, la somma dei vincoli esterni e del numero delle aste (condizioni di vincolo) deve essere uguale al numero dei nodi moltiplicati per due (gradi di libertà)

Ve + a = 2 n

3 + 11 = 2 * 7

14 = 14    (isostatica)

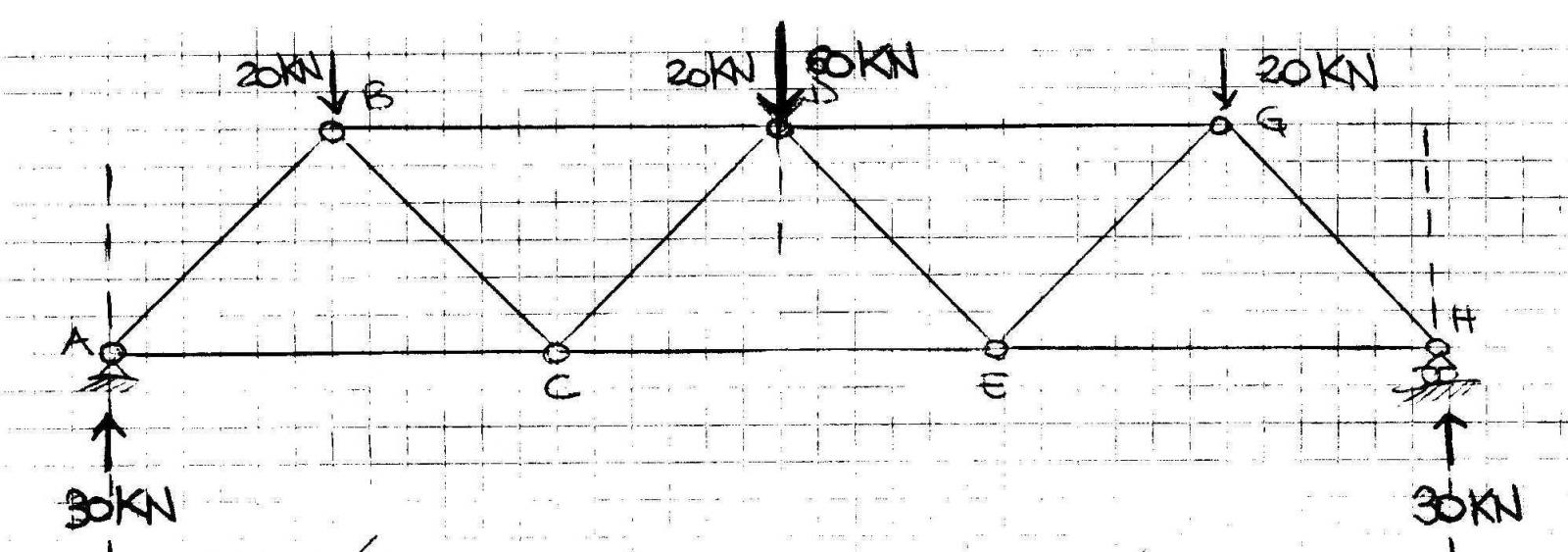
2) Equilibrio per Vincoli Esterni

La risultante delle tre forze applicate si trova proprio sull'asse di simmetria ed è pari a 60 KN. Le reazioni dei vincoli esterni saranno parallele alla risultante, di verso opposto e di valore dimezzato (30 KN).

3) Metodo di Ritter

Siccome la struttura è simmetrica se ne risolve solo una metà. Per conoscere il comportamento delle aste si utilizza il metodo di Ritter: si effettuano tre sezioni sulla struttura, tagliando tre aste non convergenti nello stesso punto, e successivamente si calcolano gli sforzi assiali delle aste attraverso l'equazione di equilibrio al momento del nodo preso in considerazione.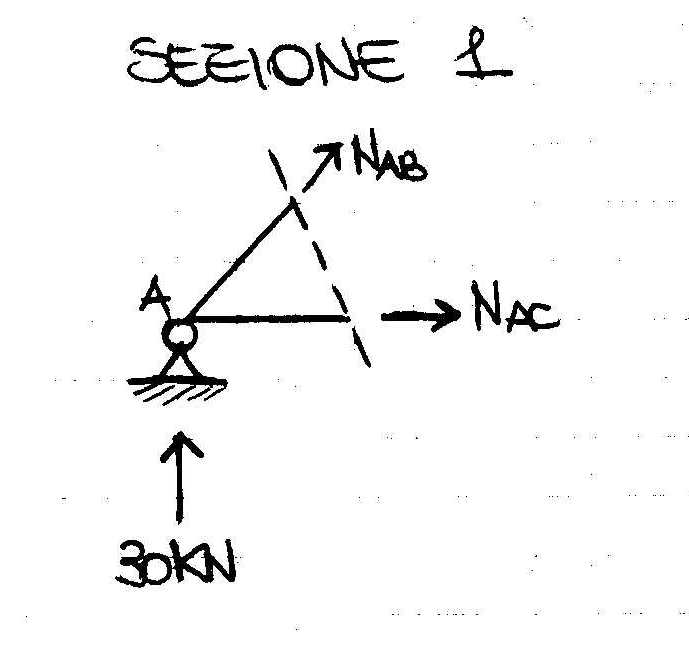

∑MB=0     -30KN*2+NAC*2=0     NAC=30KN   (asta tesa)

∑MC=0    -30KN*4-NAB2√2=0    NAB=-30√2KN   (asta compressa)

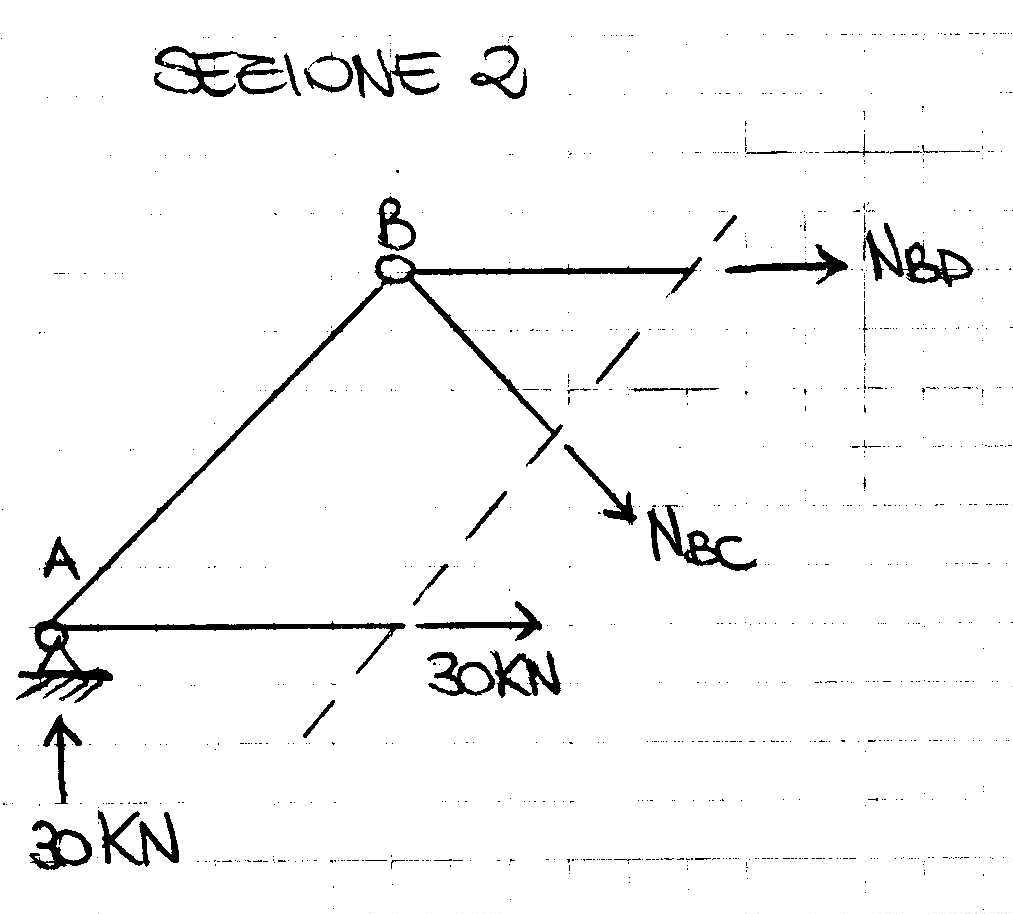
∑MC=0    -30KN*4+20KN*2-NBD*2=0      NBD=-40KN   (asta compressa)

∑MD=0   -30KN*6+20KN*4+30KN*2+NBC2√2=0     NBC=10√2KN   (asta tesa)

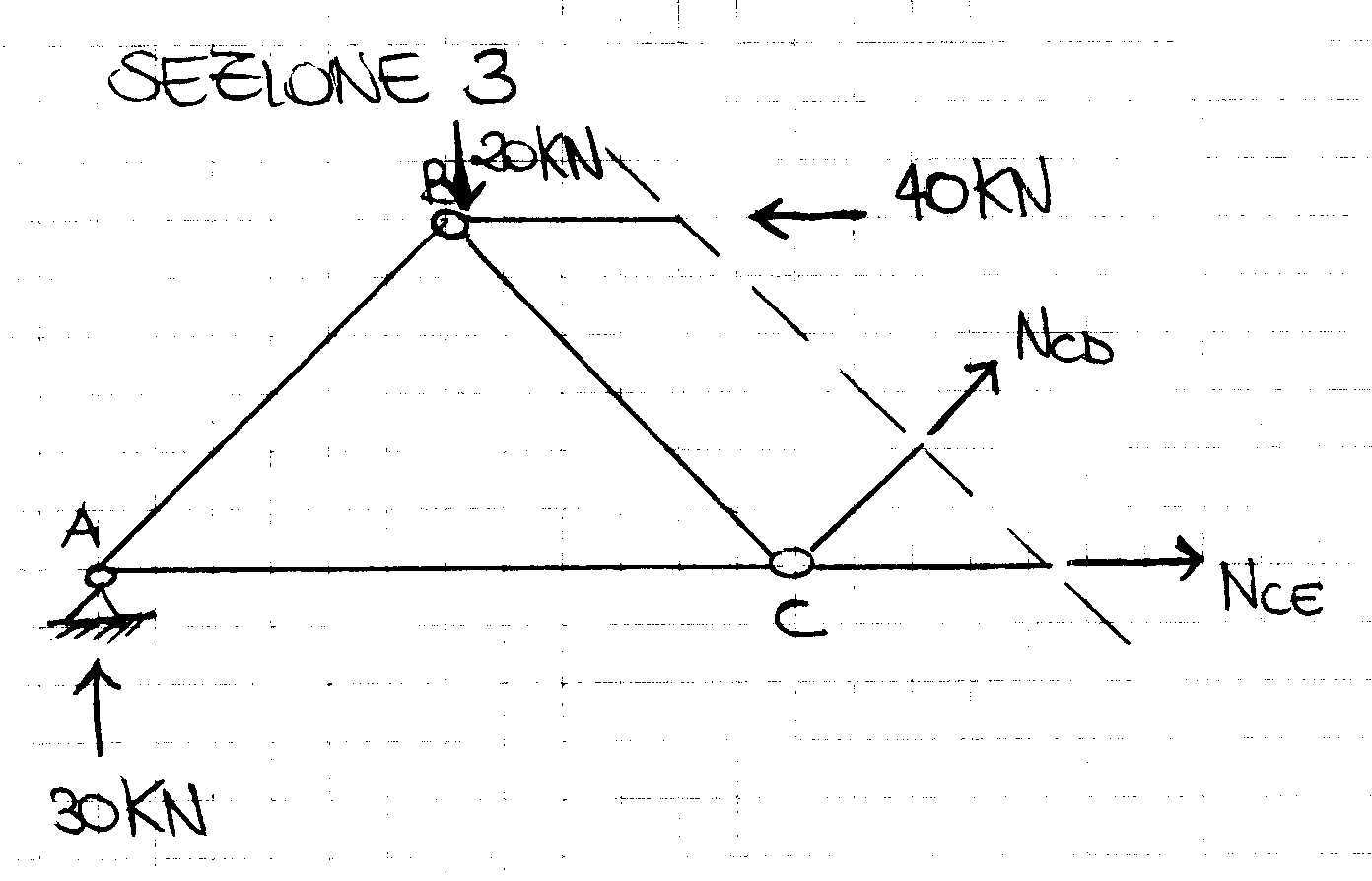
∑MD=0   -30KN*6+20KN*4+NCE*2=0   NCE=50KN   (asta tesa)

∑ME=0   -30KN*8+20KN*6+40KN*2-NCD2√2=0        NCD=-10√2KN    (asta compressa)

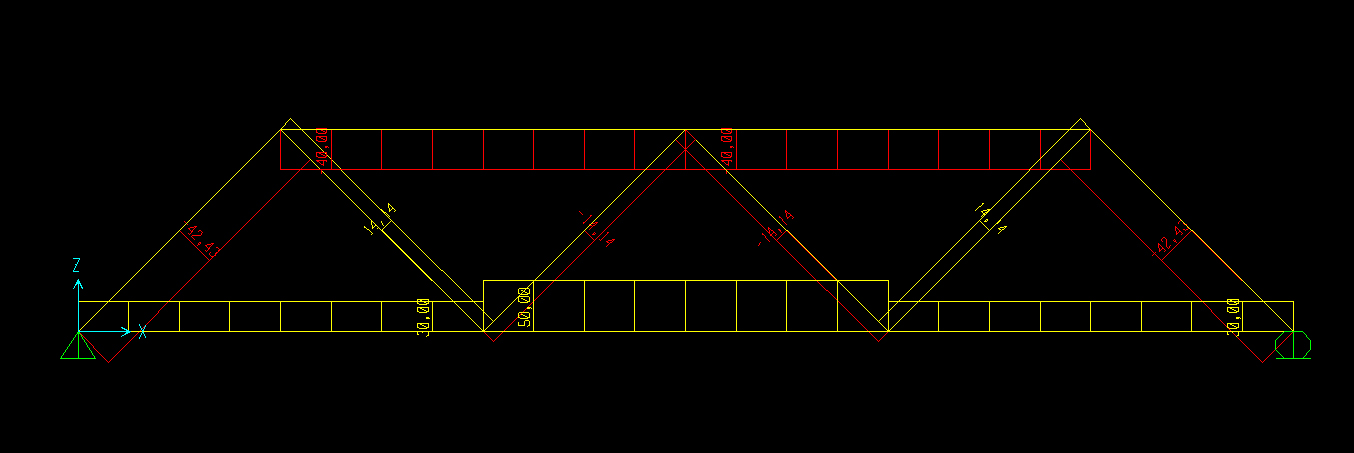
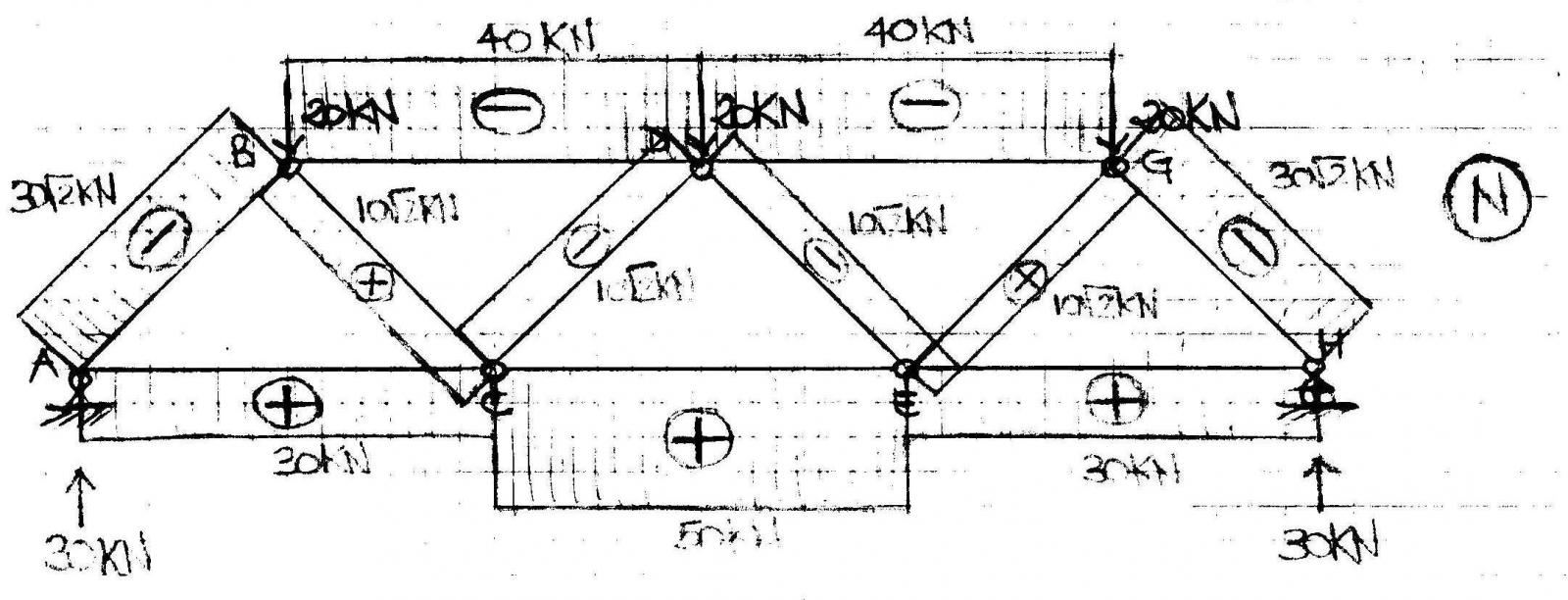
4) Diagramma dello Sforzo Normale

Quando le strutture reticolari sono caricate solo sui nodi, le aste sono sollecitate solo a sforzo normale. Dove lo sforzo normale è positivo, l'asta lavora a trazione e viene chiamata tirante, mentre dove è negativo l'asta lavora a compressione e viene denominata puntone.

5) SAP 2000

Per avere conferma dei risultati ottenuti, risolviamo l'intera struttura con il programma SAP 2000.

Grafico Deformata

Diagramma dello Sforzo Normale