STRUTTURA RETICOLARE ASIMMETRICA

1) Verifica dell'isostaticità

Affinchè una struttura reticolare sia isostatica, la somma dei vincoli esterni e del numero delle aste (condizioni di vincolo) deve essere uguale al numero dei nodi moltiplicati per due (gradi di libertà).

Ve + a = 2 n

2A + 1H + 11 = 2 * 7

14 = 14   (isostatica)

2) Equilibrio per Vincoli Esterni

La risultante delle due forze applicate è pari a 20KN e la sua retta d'azione incontra quella della reazione del carrello e quella della reazione della cerniera esterna in un punto; ciò vuol dire che la struttura è in equilibrio. Con il poligono delle forze otteniamo il verso delle reazioni dei vincoli esterni. Inoltre la reazione della cerniera esterna (RA) avrà una componente orizzontale (RuA) ed una verticale (RvA).

Poligono delle Forze

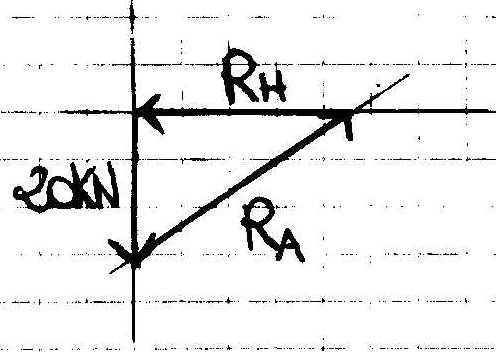
Componenti di RA

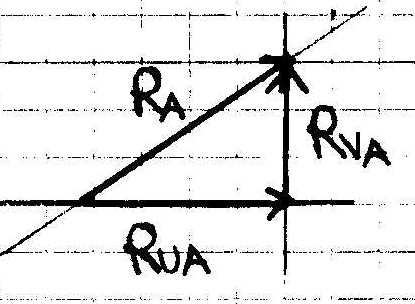
Riepilogo sulla Struttura

Risolvendo le equazioni di equilibrio otteniamo i valori delle reazioni incognite.

∑Fx=0       RuA-RH=0        RuA=RH

∑Fy=0       RvA-10KN-10KN=0      RvA=20KN

∑MA=0     -10KN*1-10KN*2+RH*1=0       RH=30KN

3) Metodo dei Nodi

Per conoscere il comportamento delle aste si utilizza il metodo dei nodi: si isola un nodo della struttura alla volta e poi si calcola il valore dello sforzo assiale di ogni asta, risolvendo le equazioni di equilibrio alla traslazione verticale e orizzontale.

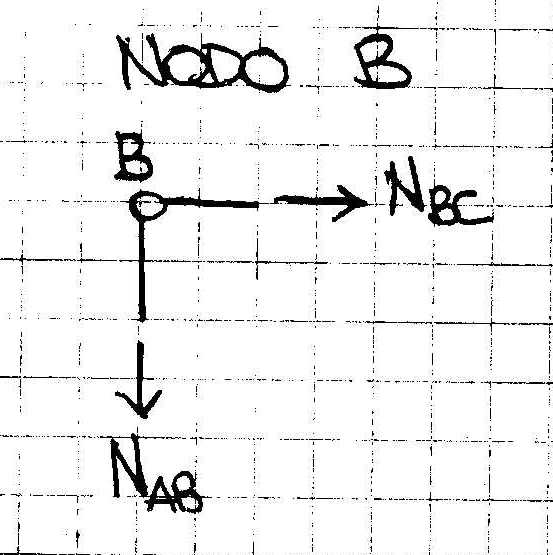
∑Fx=0      NBC=0   (asta scarica)

∑Fy=0      NAB=0   (asta scarica)

∑Fx=0      30KN+NAD+NAC√2/2=0      NAD=-10KN   (asta compressa)

∑Fy=0      20KN+NAC√2/2=0       NAC=-20KN√2       (asta compressa)

∑Fx=0      10KN+NDG=0       NDG=-10KN       (asta compressa)

∑Fy=0      NCD=0      (asta scarica)

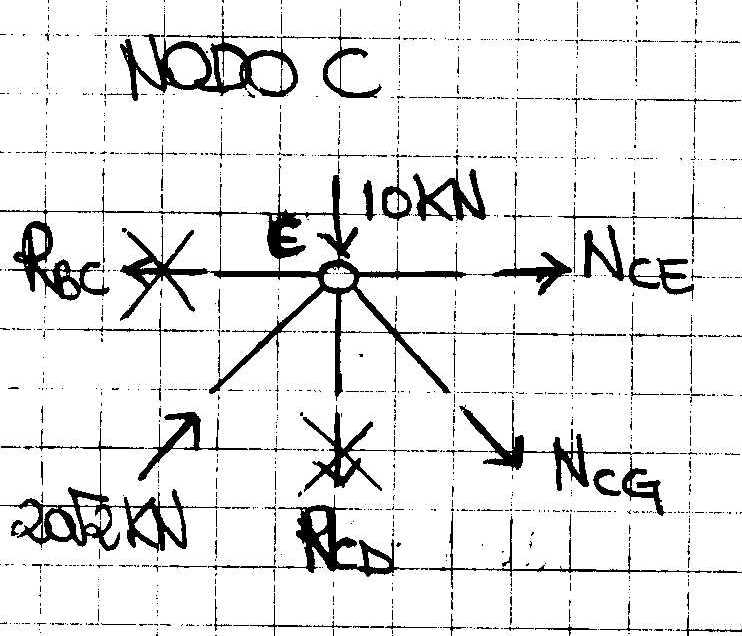
∑Fx=0      NCE+NCG√2/2+20√2KN*√2/2=0      NCE=-30KN      (asta compressa)

∑Fy=0      -10KN+20KN-NCG√2/2=0       NCG=10KN√2       (asta tesa)

∑Fx=0      30KN+NEH=0     NEH=-30KN     (asta compressa)

∑Fy=0      -10KN-NEG=0     NEG=-10KN     (asta compressa)

∑Fx=0      -NGH√2/2=0       NGH=0       (asta scarica)

4) Diagramma dello Sforzo Normale

Quando le strutture reticolari sono caricate solo sui nodi, le aste sono sollecitate solo a sforzo normale. Dove lo sforzo normale è positivo, l'asta lavora a trazione e viene chiamata tirante, mentre dove è negativo l'asta lavora a compressione e viene denominata puntone.

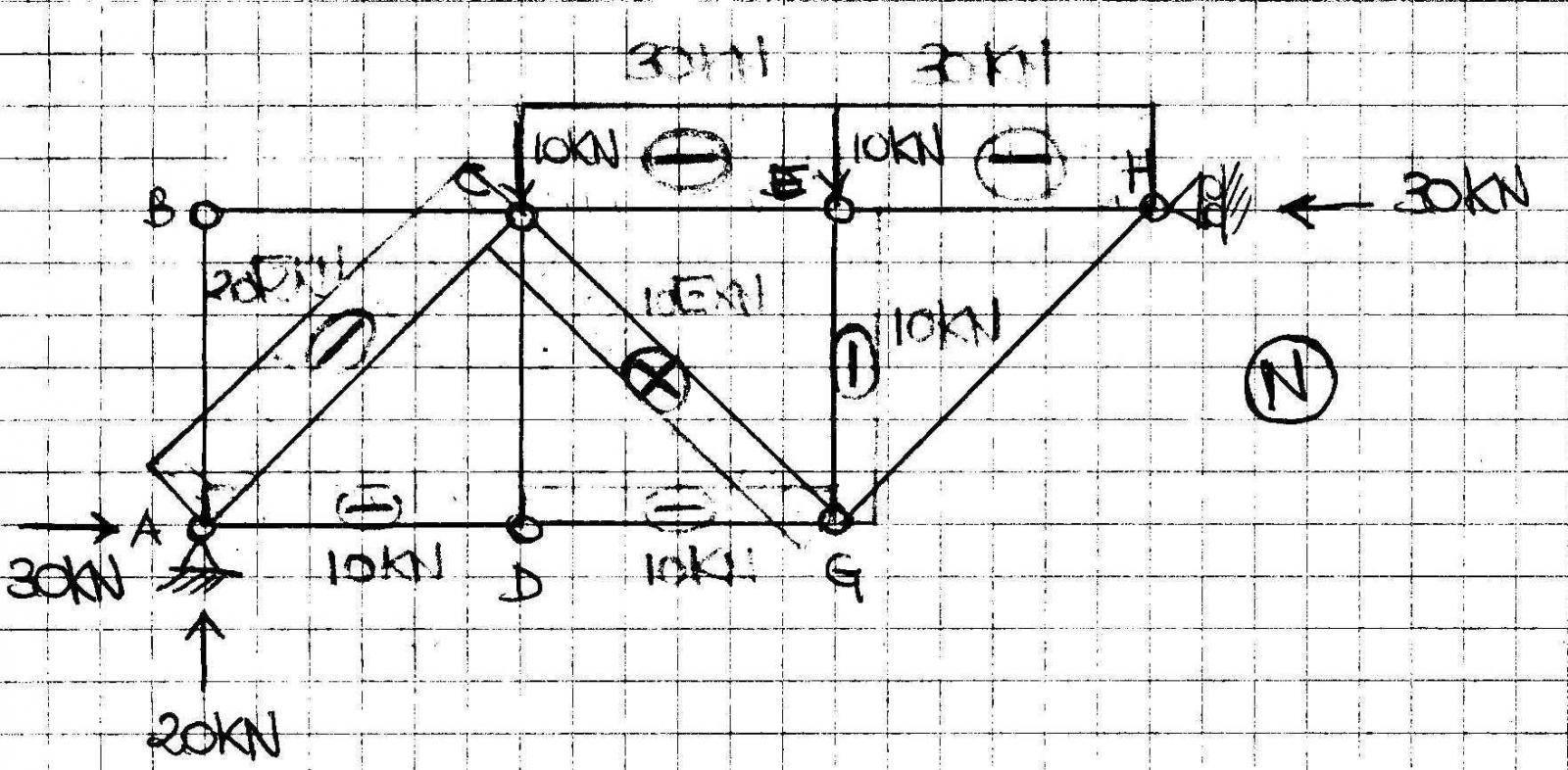
5) SAP 2000

Per avere conferma dei risultati ottenuti, risolviamo l'intera struttura con il programma SAP 2000.

Grafico della Deformata

Diagramma dello Sforzo Normale