blog di Mauro.Rocchi

In questa esercitazione analizzeremo un impalcato strutturale soggetto a spinte orizzontali (vento,sisma,ecc...). Se consideriamo una struttura compasta da soli travi e pilastri, oltre a resistere ai carichi verticali, se diposta correttamente può sopprtare anche i carichi orizzontali e quindi può agire da controvento.

Esaminiamo un impalcato tipo in cls armato, composto da 14 pilastri di sezione rettangolare 30x40 cm (2 momenti d'inerzia differenti uno lungo l'asse x e lungo l'asse y)

quindi:

E= 21000 N/mm²

I_x=bh³/12 = 90000,00 cm⁴ (pilastri A1,A2,B1,B2)

I_Y=hb³/12 = 160000,00 cm⁴ (pilastri C1,C2,C3,C4,C5,D1,D2,D3,D4,D5)

dato che i controventihanno un comportamento elastico, posso rappresentarli con delle molle.

 

 

1) Calcolo delle regidezze traslanti dei controventi dell'edificio

in queste tabelle riportiamo i valori del modulo elastico, l'altezza dei pilastri e i valori dei momenti d'inerzia.

2) Tabella sinottica controventi e distanze

sono riportate li distanze orizzontali e verticali dall'origine O

3) Calcolo del centro di massa

Per calcolare il centro di massa ho diviso la struttura in 2 aree, una di 168 m² e l'altra di 60 m². Successivamente ho inserito le distanze dei loro baricentri dall'origine O in manieta le da ricavarci le coordinate dell'impalcato.

4) Calcolo del centro delle rigidezze e delle rigidezze globali.

Nella tabella sono riportate le coordinate del centro delle rigidezze, le distanze di ogni controvento dal centro delle rigidezze e la rigidezza torsionale che si ottine attraverso la sommatoria di ogni rigidezza moltiplicata per la distanza al quadrato dal centro delle rididezze.

5) Analisi dei carichi sismici

6-7) Ripartizione della forza sismica lungo x e y

le 2 tabelle riportano i valori del momento torcente della struttura, le traslazioni e le rotazioni lungo x e y.

 

 

 

 

 

 

In questo esercizio analizziamo una trave vierendeel, composta da due correnti orizzontali collegati da montanti verticali, nel quale tutti i nodi sono ad incastro.

 

La trave può essere rappresentata come un modello Shear-Type, ovvero uno schema che si basa sul concetto di trave infinitamente rigida, la quale ha una rigidezza flessionale che ne impedisce la deformazione . Mentre i pilastri, collegati con nodi ad incastro, non si si deformano se sottoposti a qualsiasi sforzo assiale.

 

 

                          . 

 

 

Inizio a calcolare i valori del taglio grazie all'equazione di equilibrio alla traslazione analizzando ogni tratto (da 1 a 6) della struttura. 

 

 

 

Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:

 

 

Mentre per trovare il valore del momento agli estremi delle aste orizzontali mi basta moltiplicare il valore del taglio per metà della lunghezza (l/2).

 

 

 

deformata:

 

 

Possiamo notare dal diagramma della deformata, che la curvatura è nulla nel punto di flesso(in mezzeria) e di conseguenza anche il momento sarà nullo.

 

 

Ora mi calcolo momento e taglio delle aste verticali:

Per il momento faccio l'equilibrio alla traslazione:

 

 

alcolo i valori dei tagli, equilibrando ai momenti appena ricavati una coppia di forze:

 

 

 

 

Diagramma del Taglio

              

 

 

 

Diagramma del Momento

 

 

_____________________________________________________________________________________________________________________________________________________________

 

 

 

Abbiamo analizzato un' altro esempio di trave Vierendeel vincolata a entrambi i bordi e ne abbiamo calcolato gli spostamenti ed i diagrammi di taglio e momento sugli elementi orizzontali e verticali. Questa volta l'esercizio risulta semplificato perchè si può sfruttare la simmetria di questo schema strutturale.

 

 

 

Come fatto nell'esercizio precedente calcolo i valori di taglio partendo dall'asta centrale.

 

 

 

 

 

 

Disegno il diagramma del taglio per gli elementi orizzontali:

 

 

 

 

 

Per trovare i valori dei momenti, mi basta anche qui moltiplicare il valore del taglio per metà della

lunghezza (l/2).

 

 

Deformata:

 

 

 

Ora mi calcolo momento e taglio delle aste verticali 

 

Equilibrio dei nodi:

 

 

 

Equilibrio delle aste:

 

 

Diagramma del Taglio

 

 

 

 

Diagramma del Momento

 

 

 

 

 

 

L'esercizio consiste in una struttura 3 volte iperstatica. Per risoleverla la trasfomo in un sistema isostatico trasformando i carrelli B-C-D in cerniere interne, dividendo cosi la struttura in 4 corpi separati. Inoltre applico dei momenti flettenti X1, X2 e X3 in modo da ripristinare la rigidità della trave.

 

Trovo il valore dei tre momenti X₁,X₂ e X₃ (data la simmetria della struttura X₁ = X₃):

Sappiamo che ΔφB=ΔφD=0 e ΔφC=0

Uguaglio valori della rotazione di sinistra con quelli di destra e ricaviamo X1 e X2.

 

Dopo aver trovato le 2 incognite mi calcolo le reazioni vincolari:

 

                          +  

                                            

 

                          =

 

Infine disegno i diagrammi del taglio e del Momento trovando i valori nei diversi punti.

Taglio

Momento 

      

 

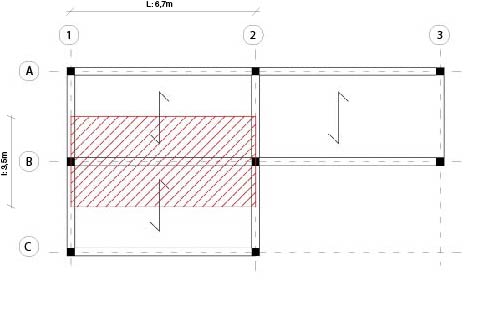
Disegno un solaio con una struttura in acciaio ipotizzando che la destinazione d’uso di questo edificio sia di tipo residenziale e prendo in analisi la trave sottoposta a maggiore sollecitazione (trace B):

 

L = 6,7 m

I= 3,35 m

 

 

 

ANALISI DEI CARICHI:

 

Qa (carichi accidentali) : 2,00 Kn/mq

 

Qp (carichi permanenti) : 3,02 Kn/mq

 

Isolante termoacustico (sp. 4cm): 7 Kn/mc = 0,28 KN/mq

 

Massetto (sp. 4cm): 21,00 KN/mc x 0,04 m = 0,84 KN/mq

Pavimento in gres porcellanato (sp. 2cm): 20 Kn/mq x 0,02 = 0,4 Kn/mq

Ipotesi d'incidenza impianti e tramezzi: 1,5 KN/mq

 

 

Qs (carichi strutturale) :

 

 

scelgo una lamiera grecata A55/P600 + getto in cls spesso 11 cm, con un peso totale della soletta di

 

1,15 Kn/mq

 

 

Dimensionameto travetto:

 

 

 

 

 

Mediate il foglio elettronico ottengo un modulo di resistenza del travetto tale da rendere necessario l'utilizzo di un IPE120 con Wx = 53,2 cm3.

Un IPE120 ha Peso = 10,4 Kg/m

Per trovare il valore in mq, lo divido per la lunghezza dell'interasse, quindi faccio: 0,104 Kn/m / 1m = 0,104 Kn/mq

 

 

Dimensionamento trave:

 

 

Trovato il peso del travetto, posso calcolarmi nuovamente Qs = 1,25 Kn/mq

 

Qs = 1,25 Kn/mq

Qp = 3,02 kn/mq

Qa = 2,00 Kn/mq

 

 

 

Ottenuto un modulo di resistenza pari a 492,88 cm3 mi ricavo dal profilario una IPE 300 con Wx = 557,0 cm3 e peso 42,2 Kg/m

Il peso al mq è pari a 0,12 KN/mq

A questo punto Qs(totale) = 1,25 + 0,12 = 1,37 Kn/mq

 

 

 

Verifico se Il modulo di resistenza così ottenuto non supera il valore di progetto indicato nel dimensionamento della trave (557 cm3).

502,31 cm3 < 557 cm3

La verifica è soddisfatta!

 

TRAVE RETICOLARE SPAZIALE

Per modellare la trave utilizziamo autocad. dopo di che importiamo il disegno su SAP salvato precentemente in DXF

Fatto ciò selezioni l'intero reticolo e clicco: edit > edit point > merge point > merge tollerance > 0,01 (per impostare una tolleranza di errore di 1 cm)

assegno 3 vincoli alla struttura: assign > joint restraint, utilizzando 2 carrelli e una cerniera che nn siano sullo stesso asse

 

assegno il materiale e una sezione alle aste: define > sections properties > frame sections, scegliendo un tubolare di acciaio di diametro 10 cm e spesso 0,5 cm

 

dopo aver assegnato un carico nullo alla struttura trasformo tutti i nodi in cerniere interne: assign > framerelease > moment 33=0

assegno un carico ai nodi superiori di 50 KN sull'asse z

lanciamo l'analisi con run now(considerando solo il peso nullo cliccando "do not run" su dead e modal)

per visualizzare le reazioni vincolari clicco su show forces/stresses > joint

 

per vedere quale numero è stato assegnato ad ogni asta clicco su: disply options for active window e spunto sulla voce labels.

per conoscere gli sforzi assiali delle aste faccio: display > show tables > element forces - frames