esercitazione 5_trave Vierendeel
In questo esercizio analizziamo una trave vierendeel, composta da due correnti orizzontali collegati da montanti verticali, nel quale tutti i nodi sono ad incastro.
La trave può essere rappresentata come un modello Shear-Type, ovvero uno schema che si basa sul concetto di trave infinitamente rigida, la quale ha una rigidezza flessionale che ne impedisce la deformazione . Mentre i pilastri, collegati con nodi ad incastro, non si si deformano se sottoposti a qualsiasi sforzo assiale.
. 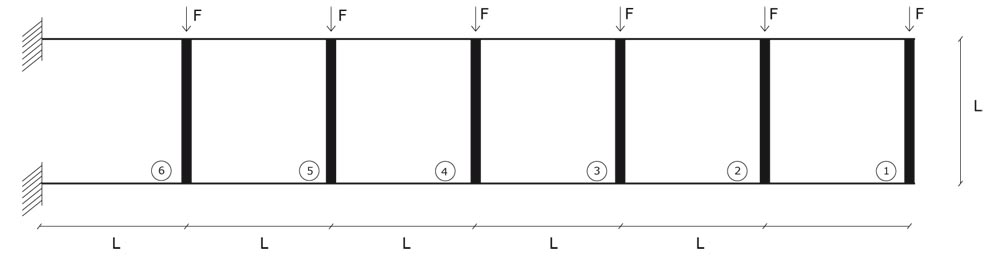
Inizio a calcolare i valori del taglio grazie all'equazione di equilibrio alla traslazione analizzando ogni tratto (da 1 a 6) della struttura.
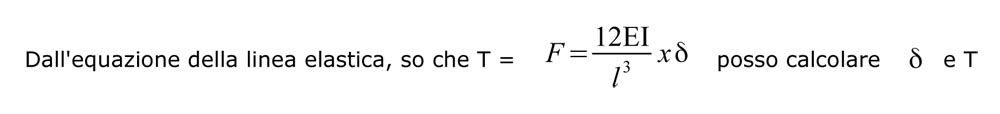

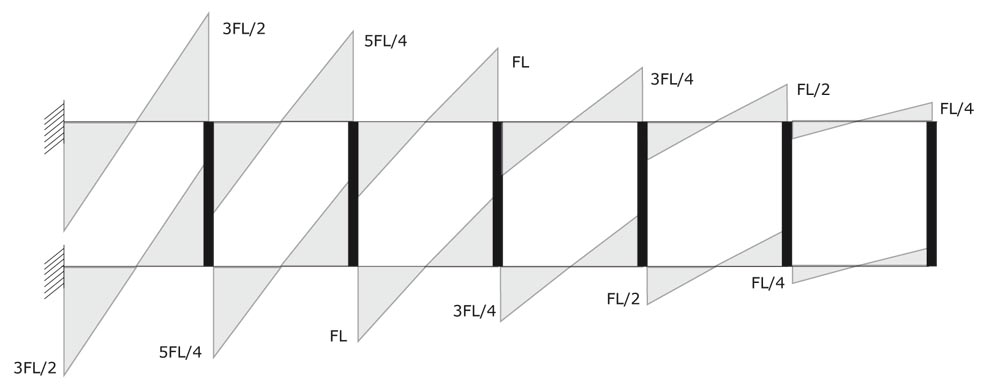
Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:
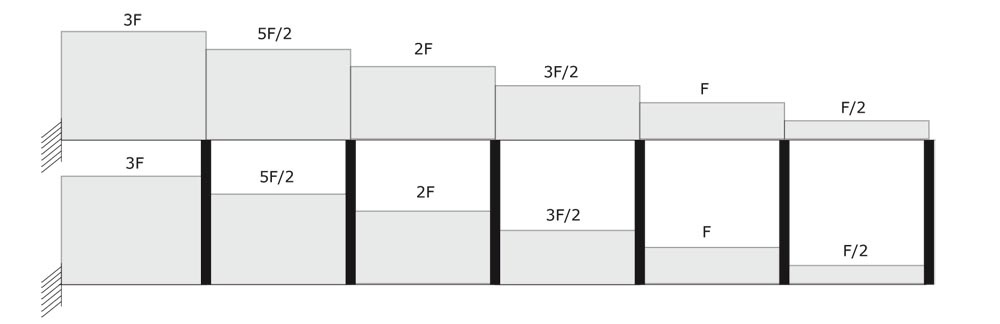
Mentre per trovare il valore del momento agli estremi delle aste orizzontali mi basta moltiplicare il valore del taglio per metà della lunghezza (l/2).
deformata:
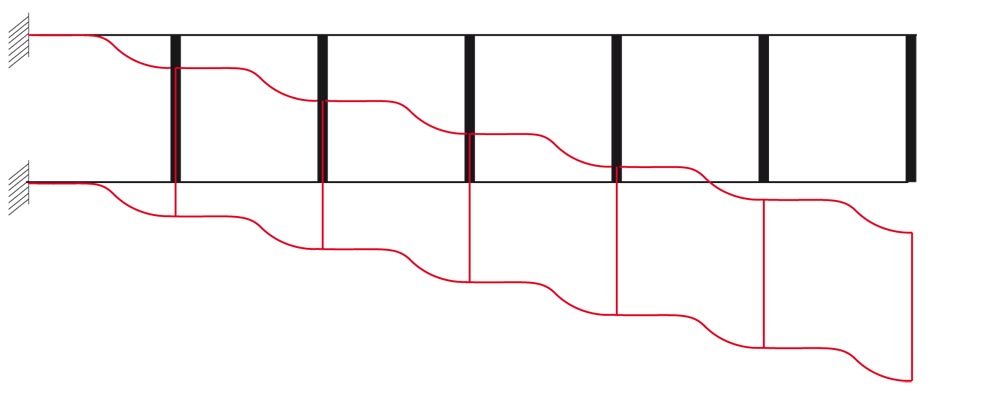
Possiamo notare dal diagramma della deformata, che la curvatura è nulla nel punto di flesso(in mezzeria) e di conseguenza anche il momento sarà nullo.
Ora mi calcolo momento e taglio delle aste verticali:
Per il momento faccio l'equilibrio alla traslazione:

alcolo i valori dei tagli, equilibrando ai momenti appena ricavati una coppia di forze:
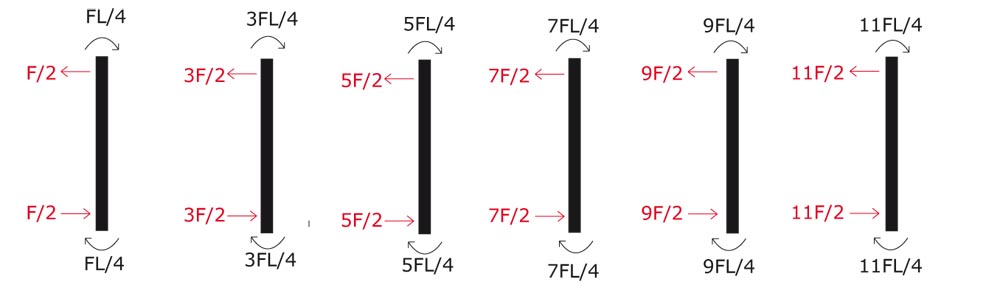
Diagramma del Taglio
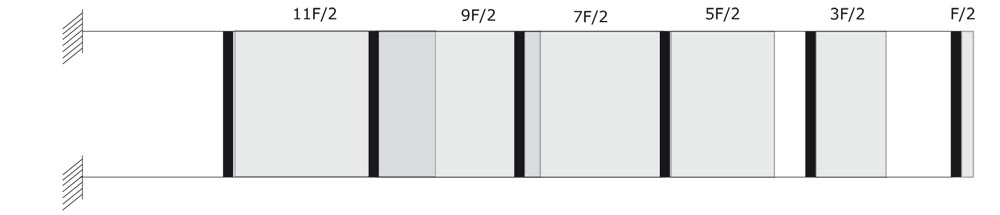
Diagramma del Momento

_____________________________________________________________________________________________________________________________________________________________
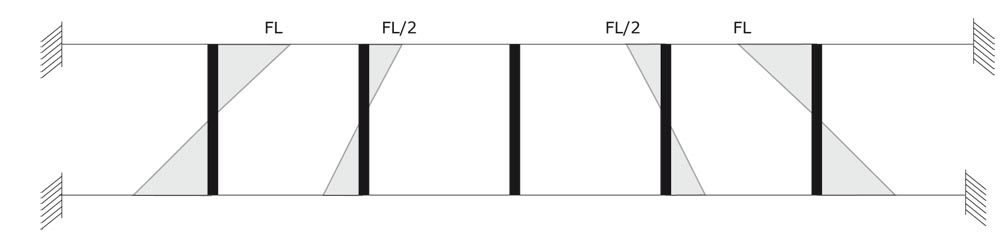
Abbiamo analizzato un' altro esempio di trave Vierendeel vincolata a entrambi i bordi e ne abbiamo calcolato gli spostamenti ed i diagrammi di taglio e momento sugli elementi orizzontali e verticali. Questa volta l'esercizio risulta semplificato perchè si può sfruttare la simmetria di questo schema strutturale.
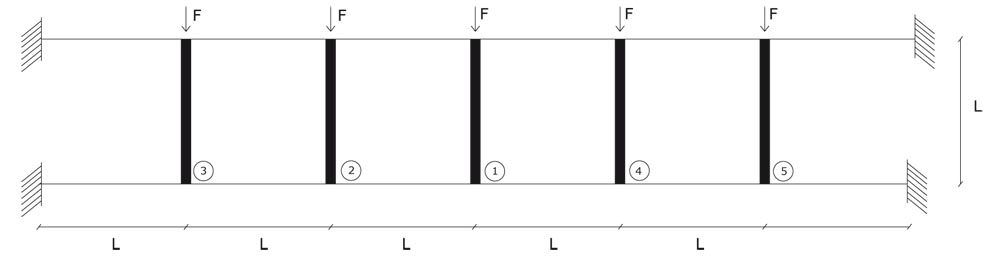
Come fatto nell'esercizio precedente calcolo i valori di taglio partendo dall'asta centrale.
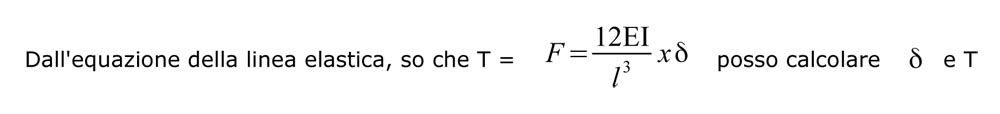

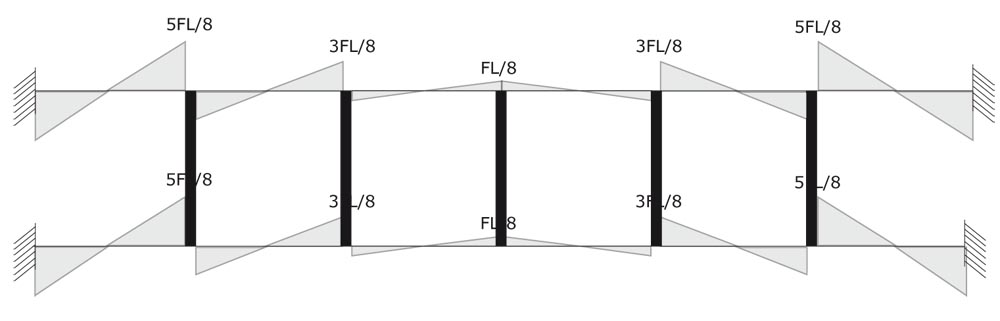
Disegno il diagramma del taglio per gli elementi orizzontali:

Per trovare i valori dei momenti, mi basta anche qui moltiplicare il valore del taglio per metà della
lunghezza (l/2).
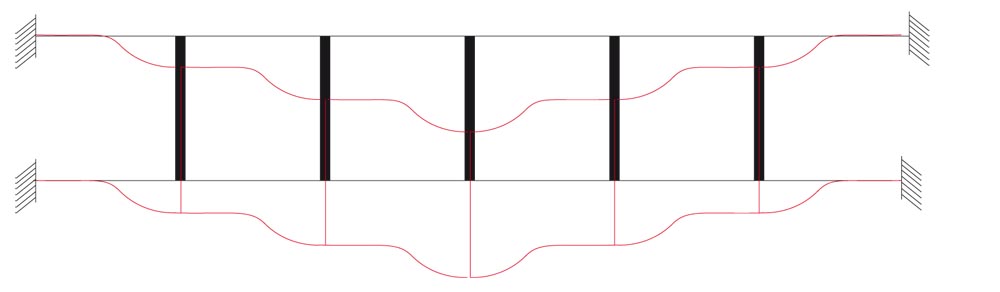
Deformata:
Ora mi calcolo momento e taglio delle aste verticali
Equilibrio dei nodi:
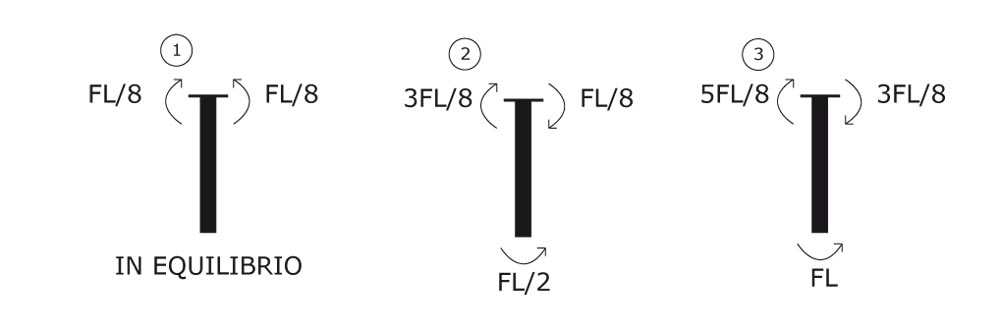
Equilibrio delle aste:
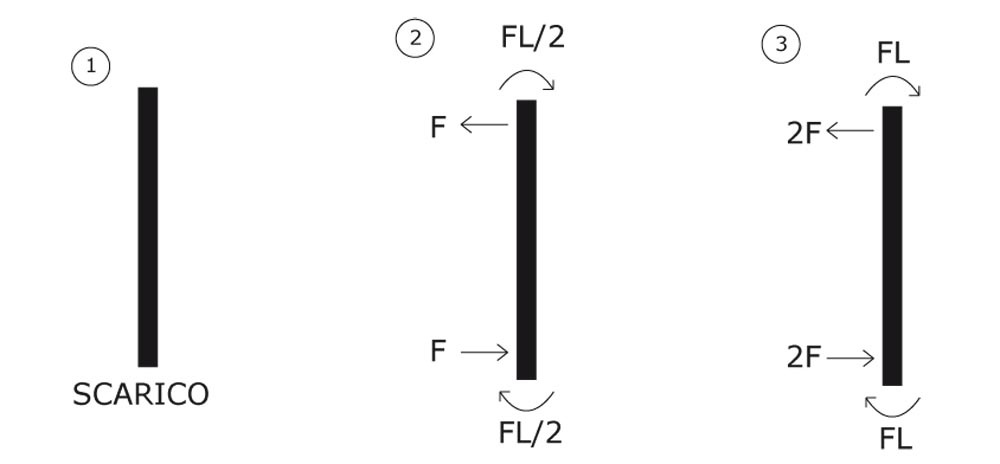
Diagramma del Taglio

Diagramma del Momento