blog di Luca.Meloni

Modelliamo i tre tipi di archi su rinoceros (da sinistra verso destra):
arco a tutto sesto (F=L)
arco ribassato (F<L)
arco parabolico (F>L)

Una volta importati su sap assegniamo il vincolo di cerniera ai punti di imposta e rilasciamo il momento in chiave cosi da creare una cerniera interna.

Assegniamo agli archi una sezione in cemento armato 30cmx40cm

Assegniamo un carico distribuito in direzione gravity projected, ovvero che agisce su una luce pari alla proiezione dell'arco.

Avviamo l'analisi.

Dai grafici delle sollecitazioni notiamo come nell'arco a tutto sesto e nell'arco ribassato siano presenti le sollecitazioni di taglio e momento, mentre nel'arco parabolico no.

Dalle reazioni vincolari è evidente la dipendenza della spinta dalla freccia (H=qL2/2F) infatti nell'arco ribassato, dove F<L la spinta è maggiore rispetto all'arco a tutto sesto e all'arco parabolico (la minore delle tre).

Definiamo un impalcato ad un piano e studiamone il comportamento a seguito dell'azione di una forza sismica. 

Indichiamo con Kv i controventi verticali e con Ko i controventi orizzontali.

Utilizzando un foglio di calcolo Excel ricaviamo le rigidezze traslanti di ogni controvento. Trattandosi di telai Shear-Type la rigidezza è calcolata con la formula [12E(I1+I2+I3+...+In)]/h3  dove E è il modulo di elasticità del materiale, (I1+I2+I3+...+In) è la somma dei momenti d'inerzia dei pilastri che compongono il controvento e h è l'altezza dei pilastri.

La seguente è una tabella di riepilogo che servirà per calcolare la posizione del centro delle rigidezze, ovvero il punto in cui si concentra la reazione dell'impalcato.

Dividendo l'impalcato in aree semplici possiamo calcolare la posizione del centro delle masse, ovvero il punto di applicazione delle forze esterne. Le coordinate del centro delle masse si trovano con le seguenti formule

XG= [A1Xg1 + A2Xg2 + A3Xg3]/Atot                 YG = [A1Yg1 + A2Yg2 + A3Yg3]/Atot

Calcoliamo la posizione del centro delle rigidezze facendo riferimento alla "tabella di riepilogo" utilizzando formule simili a quelle per il calcolo del centro delle masse

Xc = [Kv2dv2 + Kv3dv3 + Kv4dv4]/Ktot                 Yc = [Ko2do2 + Ko3do3 + Ko4do4]/Ktot

Procediamo con l'analisi dei carichi per ricavare la forza sismica orizzontale da applicare al centro delle masse. I pesi sismici sono la somma del carico totale permanente e il carico totale accidentale, quest'ultimo è ridotto dal coefficiente di contemporaneità che tiene conto delle poche probabilità che azioni diverse accadano contemporaneamente. Il peso sismico viene poi moltiplicato per un coefficiente di intensità sismica proprio della zona in cui ci troviamo.

Ricaviamo, infine, come sono ripartite le forze lungo X, Y e sui controventi orizzontali e verticali.

Verifichiamo la struttura su SAP

Modelliamo la struttura su SAP osservando i seguenti passaggi:

• assegnare alla base dei pilastri il vincolo "incastro"
• definire il centro delle masse e il centro delle rigidezze utilizzando le coordinate ricavate dal foglio Excel
• assegnare il vincolo interno "Diaphragm" a tutti i punti superiori dell'impalcato compresi il centro delle masse e il centro delle rigidezze (in questo modo facciamo si che tutti i punti si comportino come un unico oggetto) 
• assegnare la sezione rettangolare ai pilastri tenendo conto dell'orientamento di ognuno di essi
• assegnare la sezione delle travi

In SAP non è prevista la possibilità di definire un telaio Shear-Type poichè è un modello teorico. Rendiamo le travi degli elementi infinitamente rigidi aumentando di molto il loro momento d'inerzia per avere un comportamento che approssimi il più possibile quello del telaio Shear-Type.

Definiamo un nuovo caso di carico (trascurando il peso proprio) e assegniamo la forza sismica in direzione Y di intensità 67,20 Kn (come ricavato dal foglio Excel).

Avviamo l'analisi. Ci aspettiamo che l'impalcato ruoti dato che il centro delle masse e il centro delle rigidezze non coincidono.

Dalla deformata sulla destra possiamo notare come il modello creato in SAP approssimi bene il comportamento di un telaio Shear-Type. 

Analizzando gli spostamenti del centro delle rigidezze notiamo una rotazione trascurabile dato che lo spostamento massimo è di 4 decimi di millimetro in direzione Y. 

Per evitare che l'impalcato ruoti dovremmo intervenire irrigidendo i plastri nella zona sinistra, cercando di far coincidere (o avvicinare il più possibilie) il centro delle rigidezze al centro delle masse.

Individuo nel solaio la trave a sbalzo più sollecitata e la relativa area di influenza.

Utilizziamo gli stessi esempi di solai della seconda esercitazione e procediamo con il dimensionamento della trave. Affinchè il calcolo sia verificato è necessario che l'abbassamento (Vmax) dell'estremo della trave non superi 1/250 della luce. Questo rapporto è indicato sul foglio excel tramite questa formula L/Vmax > 250

SOLAIO IN LEGNO

Qs = 0,42 Kn/mq         Qp = 1,72 Kn/mq        Qa = 2,00 Kn/mq

Inseriamo i dati nel foglio di calcolo excel 

Un primo calcolo ci ha portato ad avere una trave di sezione 25 cm x 43,43 cm; scegliamo una trave di sezione 25 cm x 45 cm, ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti ad aumentare l'altezza della trave portandola a 50 cm.

Utilizzando una trave di sezione 25 cm x 50 cm il rapporto L/Vmax > 250 è verificato.

SOLAIO IN CLS

Qs = 1,8 Kn/mq        Qp = 2,4 Kn/mq        Qa = 2,00 Kn/mq

Un primo calcolo ci ha portato ad avere una trave di sezione 25 cm x 37,79 cm (32,79 cm + 5 cm di copriferro); scegliamo una trave di sezione 25 cm x 40 cm, ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti ad aumentare l'altezza della trave portandola a 45 cm.

Utilizzando una trave di sezione 25 cm x 45 cm il rapporto L/Vmax > 250 è verificato.

SOLAIO IN ACCIAIO

Qs = 2,50 Kn/mq        Qp = 1,04 Kn/mq        Qa = 2,00 Kn/mq

Un primo calcolo ci ha portato ad avere una trave che abbia Wx superiore a 669,62 cm3; scegliamo una trave IPE 330 (Wx 713,00 cm3 e Ix 11770 cm4), ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti a scegliere un profilo che abbia un momento d'inerzia Ix maggiore: IPE 360, Ix 16270 cm4.

Utilizzando una trave IPE 360 il rapporto L/Vmax > 250 è verificato.

Individuo nel solaio la trave più sollecitata e la relativa area di influenza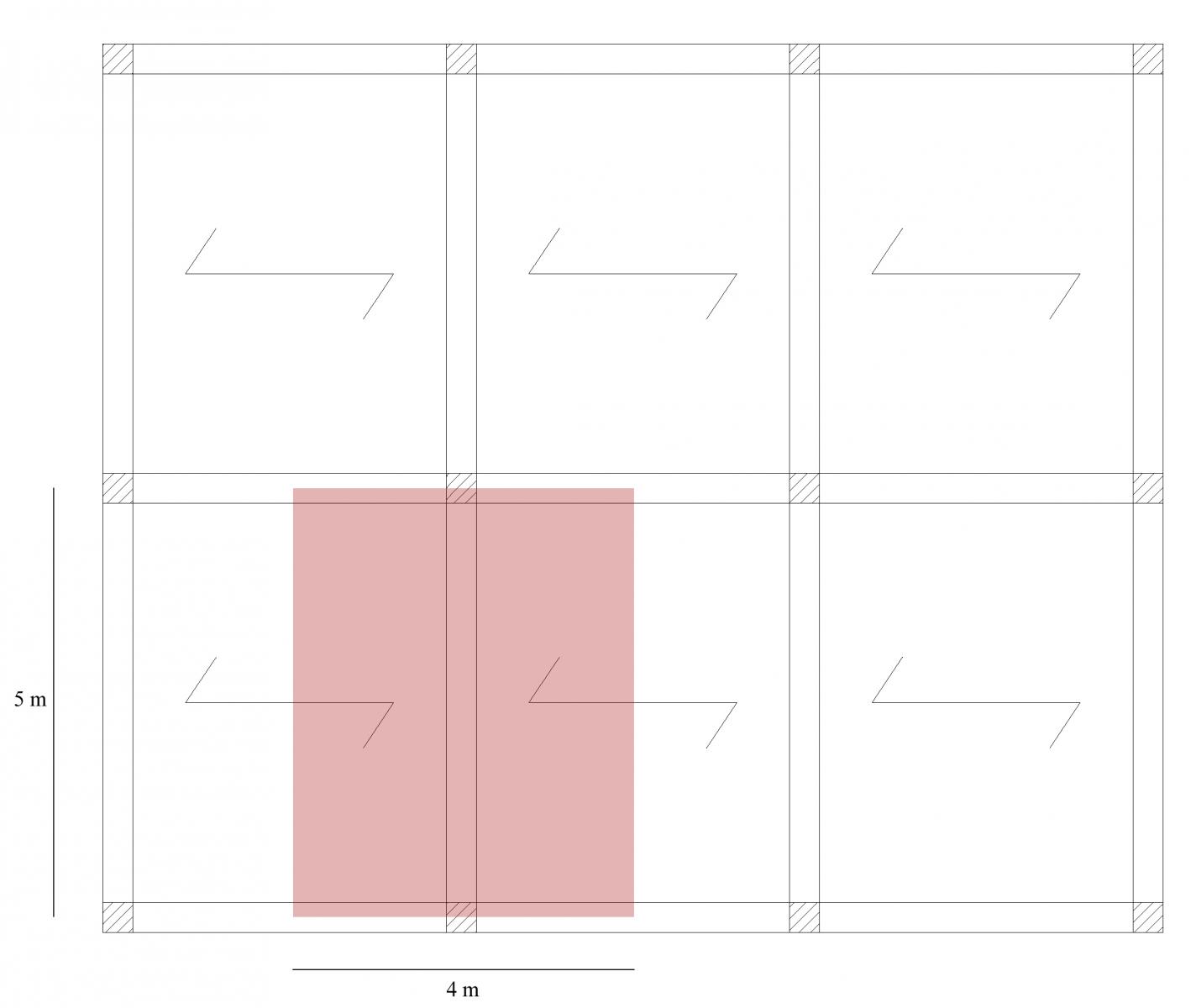

SOLAIO IN LEGNO

Procedo con il fare l'analisi dei carichi di un solaio in legno per dimensionare i travetti e successivamente le travi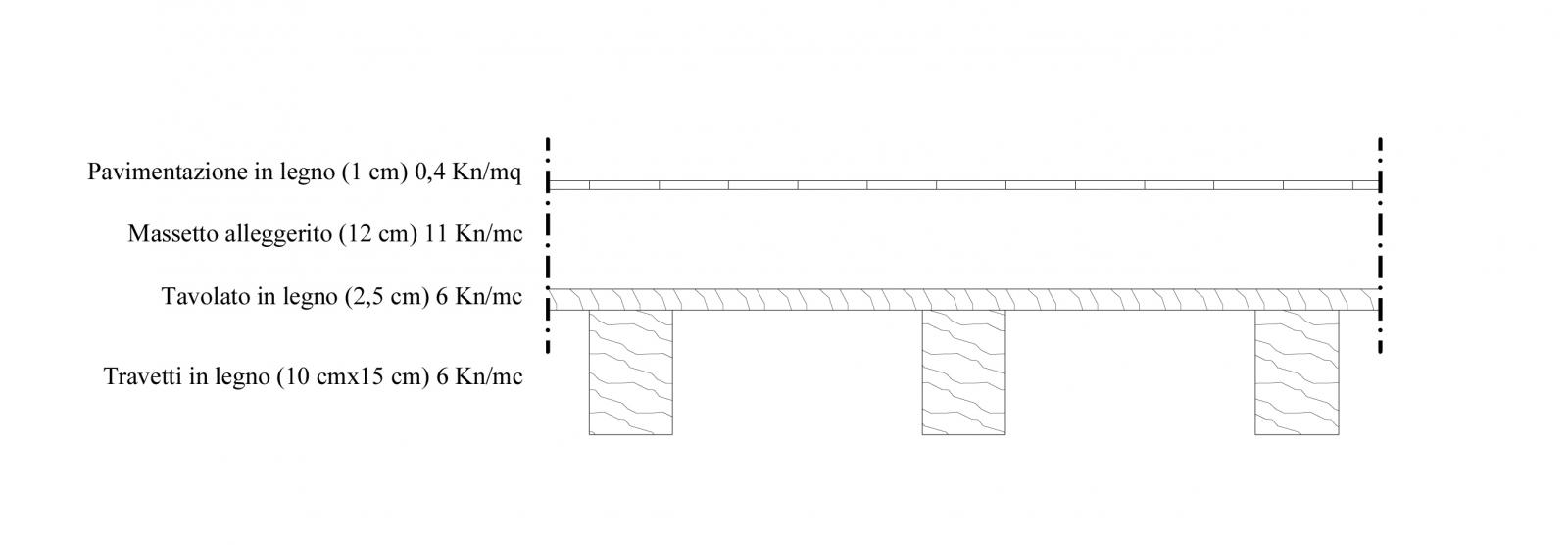

Qs = (0,025 m x 6 Kn/mc) = 0,15 Kn/mq

Qp = (0,12 m x 11 Kn/mc) + 0,4 Kn/mq = 1,72 Kn/mq

Qa = 2 Kn/mq (edificio per uffici)

Per il dimensionamento dei travetti considero un interasse di 0,4 m e una luce di 4 m

Scelgo un travetto di sezione pari a 10 cm x 15 cm. Per dimensionare la trave aggiungo il Qs dei travetti (3 in un m) al Qs precedentemente calcolato.

Qs = [(0,1 m x 0,15 m)x3]m/mq x 6 Kn/mc + 0,15 Kn/mq = 0,42 Kn/mq

Qp = 1,72 Kn/mq

Qa = 2 Kn/mq

Per il dimensionamento della trave considero un interasse di 4 m e una luce di 5 m

L'area minima della sezione della trave deve essere di 25 cm x 36, 19 cm. Scelgo quindi una Trave di 25 cm x 40 cm.

SOLAIO IN CLS

Procedo con il fare l'analisi dei carichi di un solaio in CLS per il dimensionamento della trave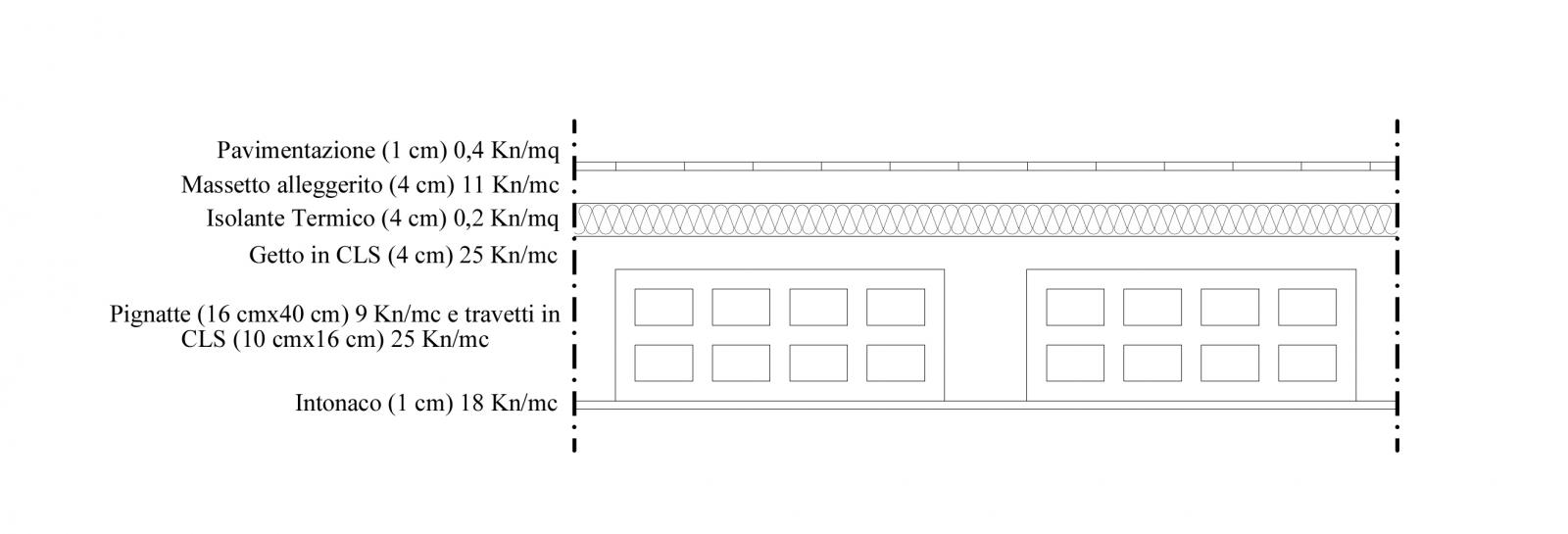

Qs = [(0,1 m x 0,16 m) x 2]m/mq x 25 Kn/mc + (0,04 m x 25 Kn/mc) = 1,8 Kn/mq

Qp = [(0,40 m x 0,16 m) x2]m/mq x 9 Kn/mc + 0,4 Kn/mq + (0,04 m x 11 Kn/m) + 0,2 Kn/mq + (0,01 m x 18 Kn/mc) = 2,4 Kn/mq

Qa = 2 Kn/mq

Ipotizzando la base della sezione di 25 cm l'altezza utile della trave è di 30,82 cm a cui vanno aggiunti 5 cm di copriferro, ovvero 35,82 cm di altezza totale. Scelgo una trave con sezione di 25 cm x 40 cm.

SOLAIO IN ACCIAIO

Procedo con il fare l'analisi dei carichi di un solaio in legno per dimensionare i travetti e successivamente le travi

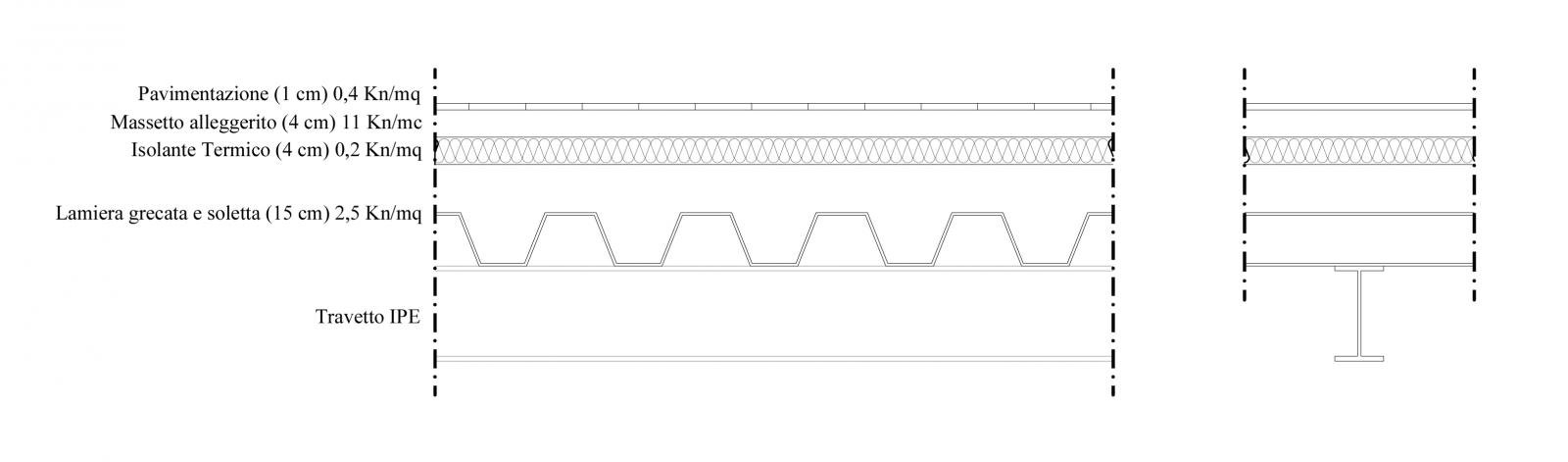
Qs = 2,5 Kn/mq (pacchetto lamiera gracata, valori in tabella)

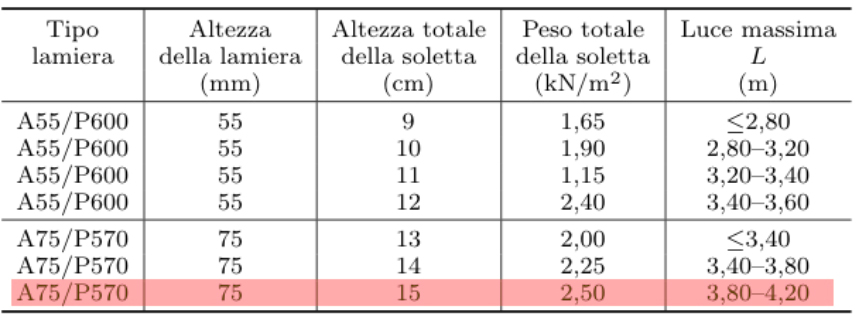
Qp = 0,4 Kn/mq + 0,2 Kn/mq + (0,04 m x 11 Kn/mc) = 1,04 Kn/mq

Qa = 2 Kn/mq

Per il dimensionamento dei travetti IPE considero un interasse di 1 m e una luce di 4 m. L'acciaio scelto è della classe Fe 360/S235

Ottenuto il modulo di resistenza minimo Wx = 74,40 cm3 lo confronto con i valori riportati sul profilario scegliendo un travetto con Wx immediatamente superiore a quello ricavato: IPE 140, Wx = 77,3 cm3

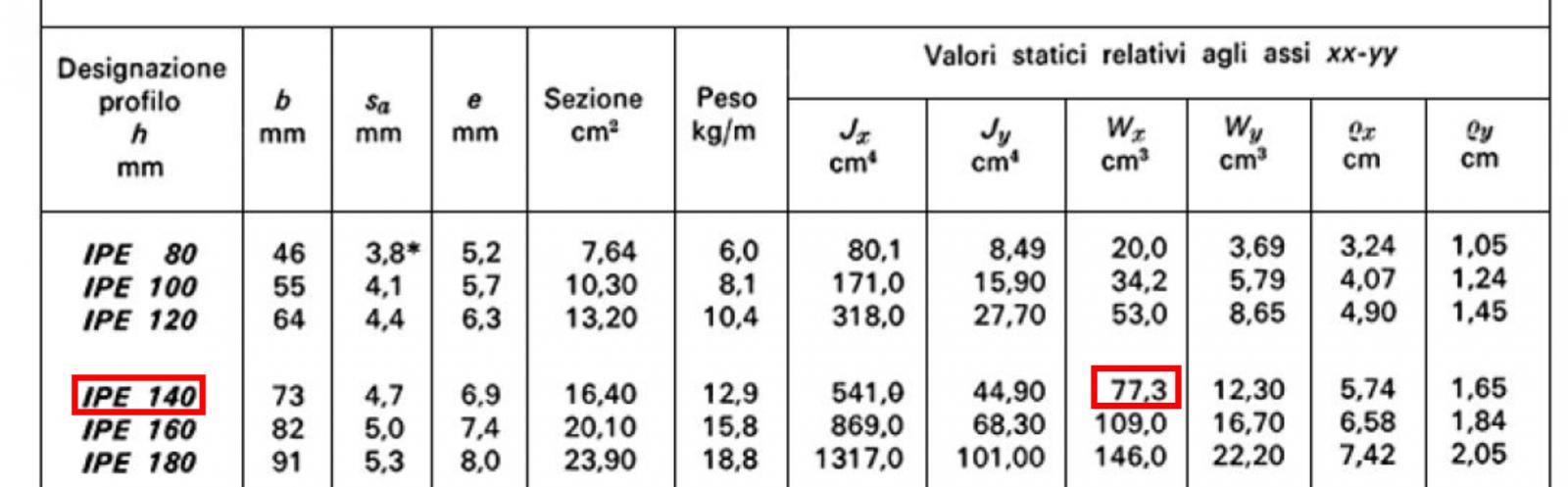
Dimensionato il travetto aggiungo il Qs del travetto in 1 m al Qs precedentemente calcolato

Qs = 2,5 Kn/mq + 0,13 Kn/mq = 2,63 Kn/mq

Qp = 1,04 Kn/mq

Qa = 2 Kn/mq

Per il dimensionamento della trave l'interasse è di 4 m e la luce di 5 m

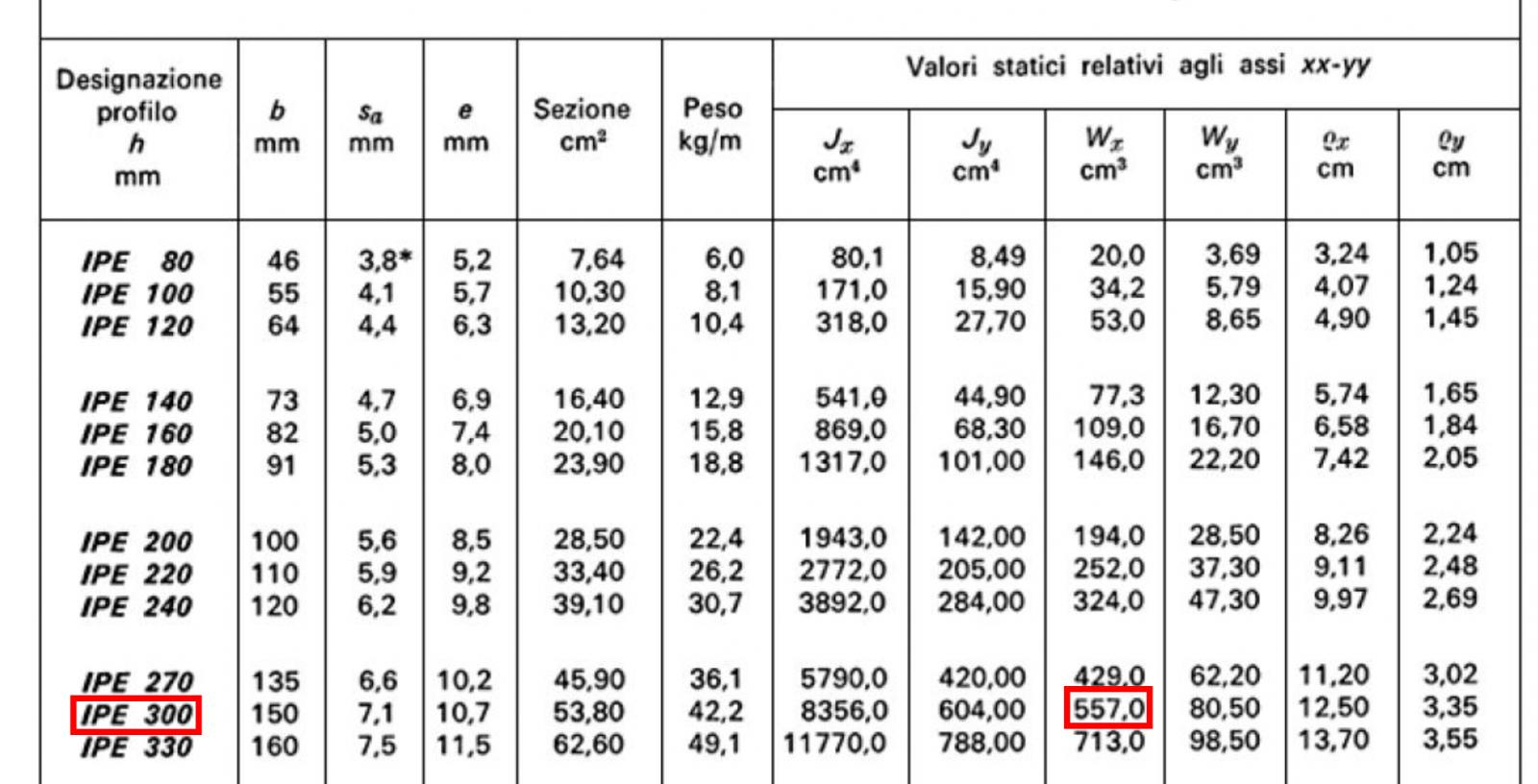
Ottenuto il Wx = 475,35 cm3 scelgo il Wx da tabella immediatamente superiore, IPE 300 Wx = 557 cm3

TRAVE RETICOLARE 2D

La prima esercitazione prevede la modellazione di una trave reticolare in 2D tramite il software SAP. Tale software ha dei modelli preimpostati di vari tipi di strutture che è possibile adattare alle proprie esigenze, nel caso della trave reticolare possiamo definire l'altezza della trave, il numero di divisioni e l'ampiezza di queste ultime.

Impostati i parametri la trave si presenta cosi:

Per rendere i nodi delle cerniere dobbiamo far si che il momento in essi sia nullo, in questo caso selezioniamo il momento 3-3 poichè è quello che agisce sul piano XZ

Definiamo una sezione in acciaio mantenendo le dimensioni predefinite da SAP e la attribuiamo a tutte le aste

Definiamo uno schema di carico che trascuri il peso proprio delle aste (peso proprio moltiplicatore=0) e lo applichiamo nei nodi scelti inserendo un valore negativo della forza (il segno meno indica la direzione lungo l'asse Z)

Adesso possiamo avviare l'analisi cosi da ricavare la deformata e i grafici delle sollecitazioni della trave

SAP ci permette di avere i valori delle sollecitazioni in forma tabellare e di esportarli su programmi esterni (Excel)

Una volta esportata la tabella su Excel possiamo identificare le aste più sollecitate e individuarle sul modello di SAP

STRUTTURA RETICOLARE 3D

Per la modellazione di un sistema reticolare in 3D iniziamo con la realizzazione di un modulo (in questo caso piramidale) per poi copiarlo nelle due direzioni X e Y fino ad ottenere la struttura desiderata.

Selezioniamo la struttura creata e tramite il comando "unisci punti" uniamo tutte le singole aste ai nodi. Il valore di tolleranza serve al programma per identificare tutte le aste entro una certa distanza (in questo caso 0,1) che devono essere unite.

Anche in questo caso dobbiamo rendere il momento nei nodi nullo, non solo nel piano XZ (momento 3-3), ma anche nel piano Y-Z (momento 2-2)

Inseriamo i vincoli, la sezione e i carichi agenti utilizzando le stesse procedure per la trave in 2D

Avviamo l'analisi ricavando la deformata, i grafici delle sollecitazioni e individuando nella tabella esportata su excel le aste più sollecitate

Salve a tutti!