blog di marco.moni

Nel seguente intervento cercherò di spiegare come sia possibile dimensionare una trave portante in tre materiali differenti (Acciao, Legno e Calcestruzzo armato), avendo a disposizione un pacchetto di solaio predefinito e velocizzando i calcoli mediante un foglio di calcolo Excel.

Prima di tutto definisco un telaio (fig.01)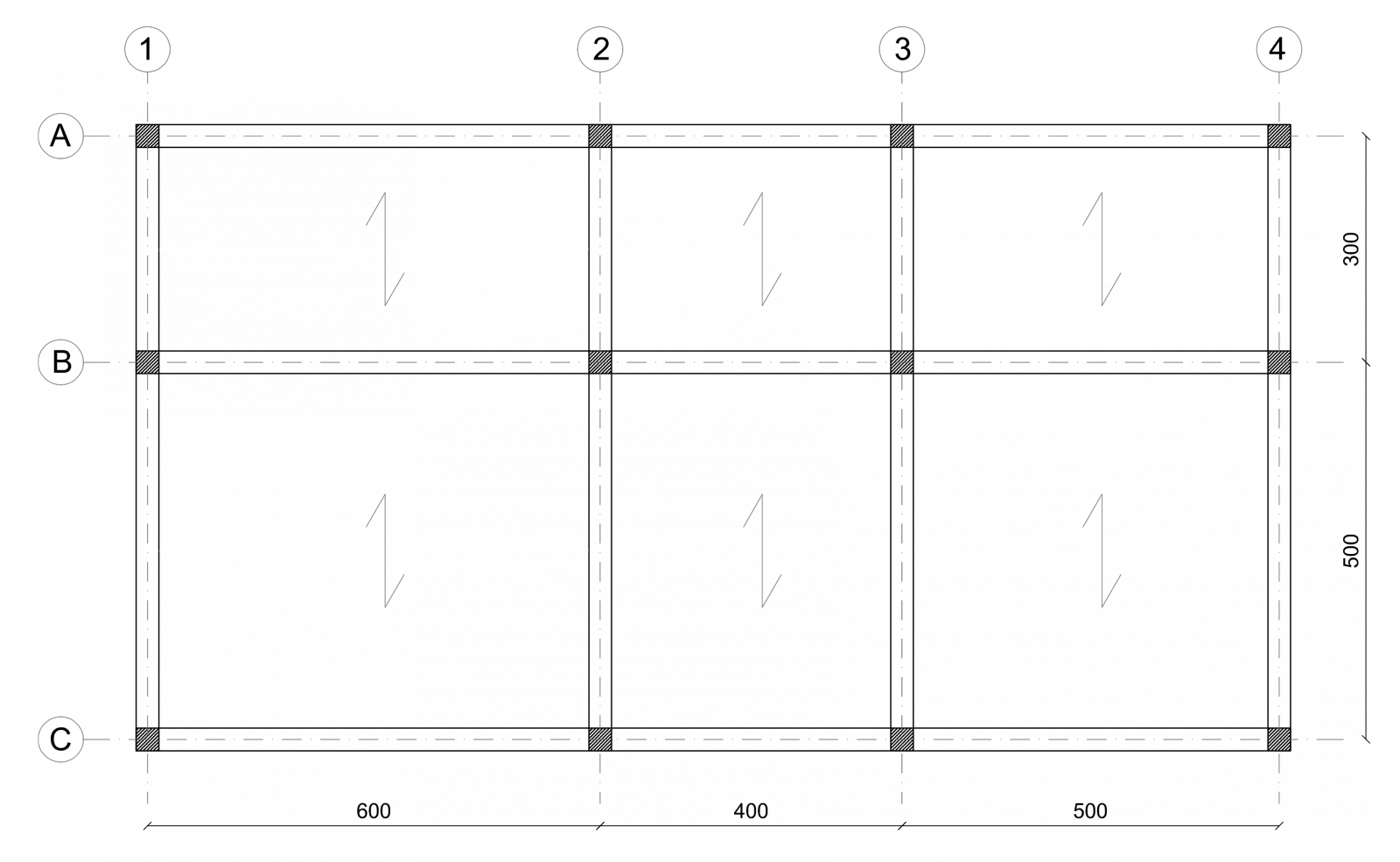

.01

Per il dimensionamento delle travi sarà sufficiente studiare l'elemento maggiormente sollecitato, ossia quello che porta la maggior porzione di solaio, in questo caso la trave B evidenziata in figura .02, la cui area di influenza è pari a 4m x 6m = 24m²

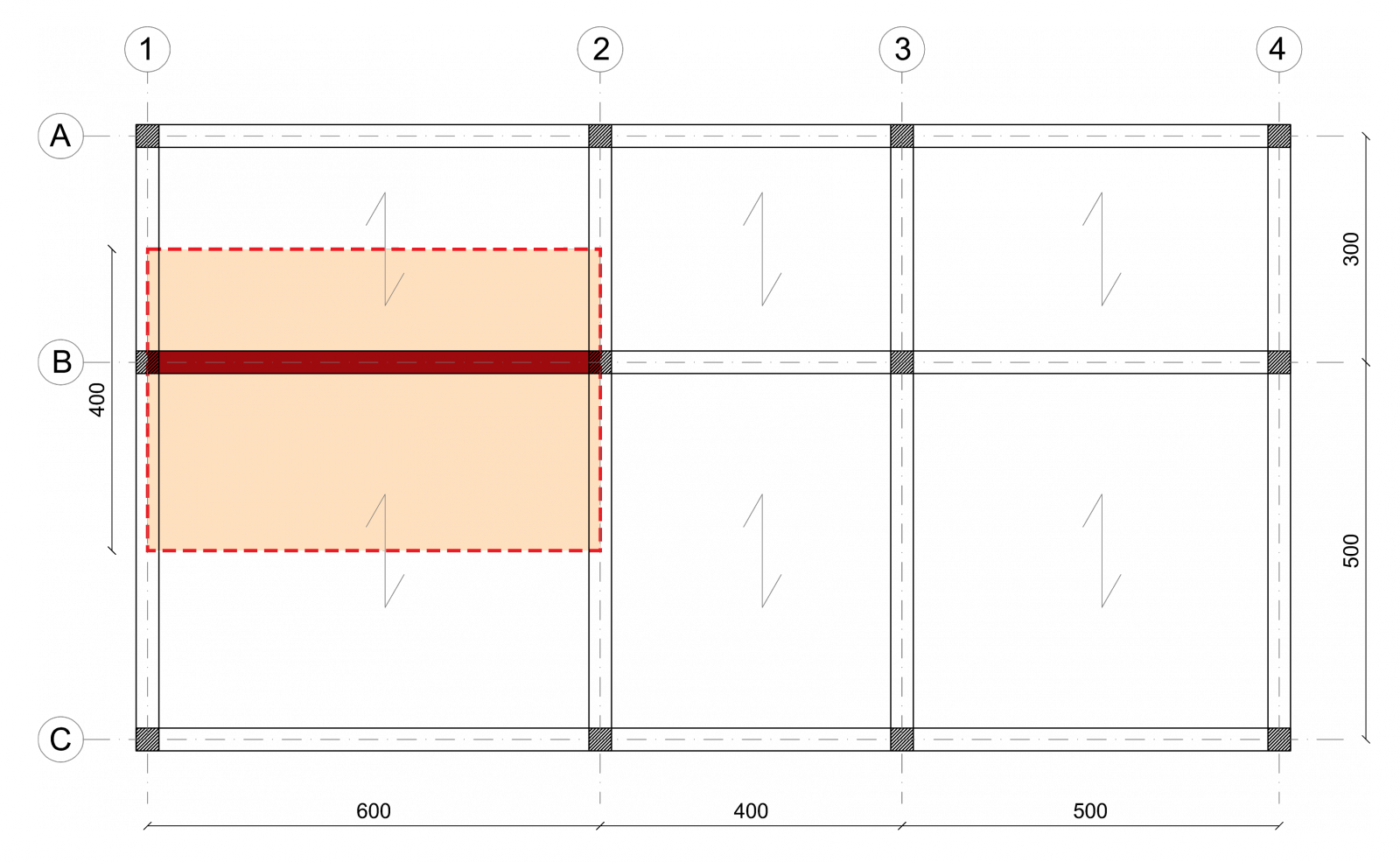.02

Devo ora differenziare il solaio a seconda della tipologia di materiale impiegato.

Solaio in ACCIAIO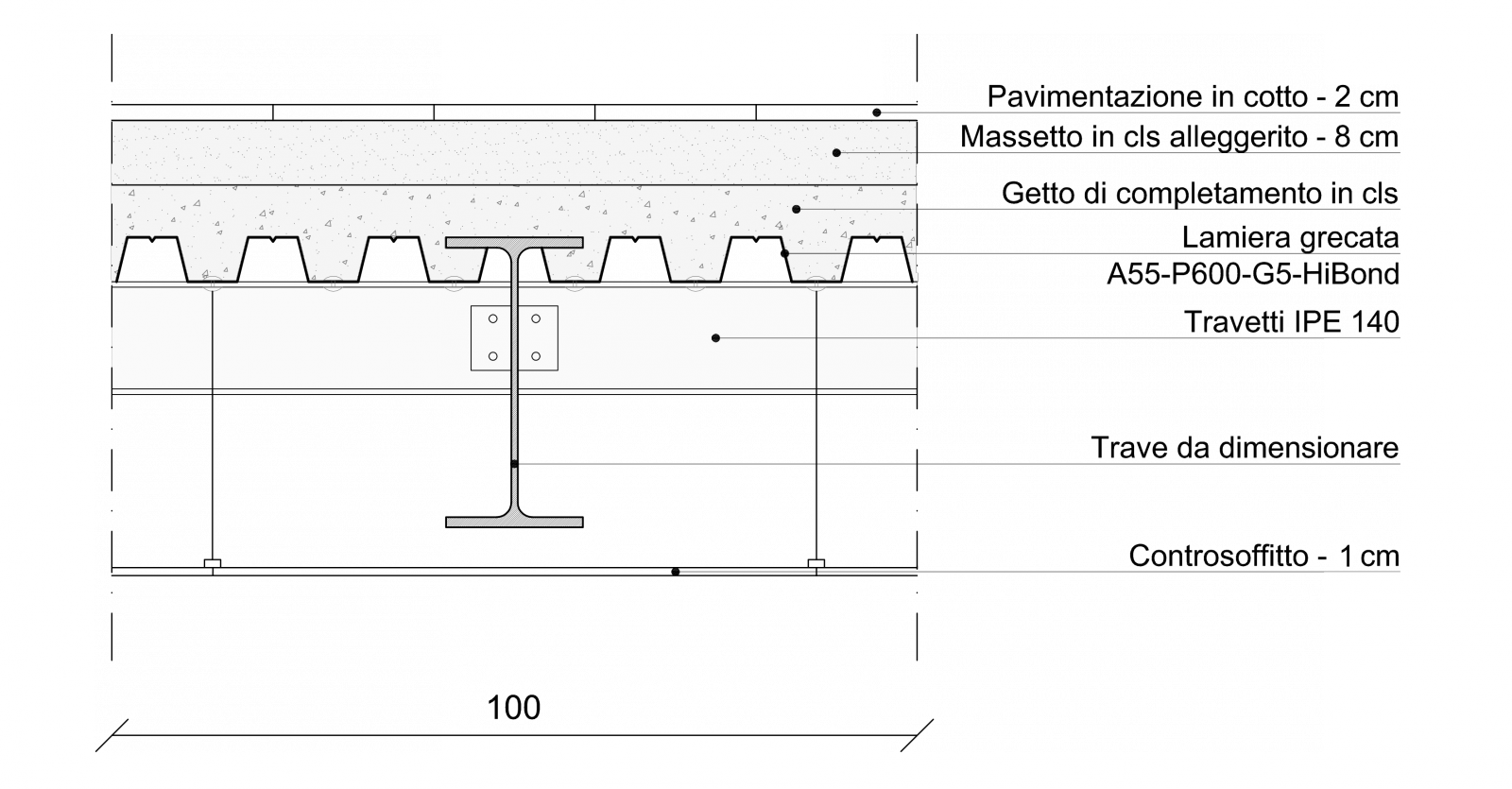

.03

Ipotizzo di avere un solaio così costituito:

Pavimentazione in cotto spessa 2 cm con un peso pari a 0,4 kN/m²

Massetto in cls alleggerito spesso 8 cm con un peso specifico di 18 kN/m³

Getto di completamento in cls di area pari a 911 cm² con un peso specifico di 25 kN/m³ 

Lamiera grecata A55-P600-G5-HiBond (fig.04) spessa 1 mm con un peso di 0,13 kN/m²

Travetti IPE 140 di area 16,4 cm² e peso specifico di 78,5 kN/m³

Controsoffitto spesso 1 cm con un peso specifico di 13 kN/m³

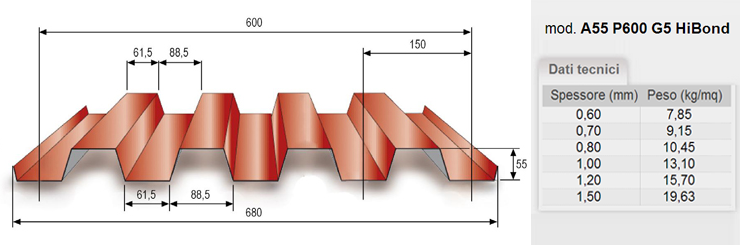
.04

Per poter dimensionare la trave devo anzitutti effettuare un'analisi dei carichi, suddividendoli in carichi strutturali, carichi permanenti e carichi accidentali che andranno poi moltiplicati per i corrispettivi coefficienti di riduzione (1,3 per i c.strutturali e permanenti, 1,5 per i c. accidentali).

Carichi strutturali (q_s):

- 2 Travetti IPE 140: 2 x 0,00164 m³/m² x 78,5 kN/m³ = 0,258 kN/m²

- Lamiera grecata: 0,13 kN/m²

- Getto di completamento in cls: 0,0911 m³/m² x 25 kN/m³ = 2,27 kN/m²

Q_Stot= 2,658 kN/m²

Carichi permanenti (q_p):

- Pavimentazione in cotto: 0,4 kN/m²

- Massetto in cls alleggerito: 0,08 m³/m² x 18 kN/m³ = 1,44 kN/m²

- Controsoffitto: 0,01 m³/m² x 13 kN/m³ = 0,13 kN/m²

A questi carichi si aggiungono poi prendendo i dati dalla normativa:

- Tramezzi: 1 kN/m²

- Impianti: 0,5 kN/m²

Q_Ptot= 3,47 kN/m²

Carichi accidentali (q_a)

I carichi accidentali sono dati dalla normativa e variano a seconda della destinazione d'uso dell'edificio. Nel nostro caso, ipotizzando un uso residenziale, si prende un valore di 2 kN/m².

Si procede quindi a tabellare i valori ottenuti nel foglio di calcolo opportunamente preimpostato, si assegna una classe di resistenza dell'acciaio pari a 275 MPa, ottenendo il momento M e  un valore Wx, pari al modulo di resistenza minimo necessario affinchè la trave possa continuare a lavorare in campo elastico (fig.05).

.05

Avendo ottenuto un W_x pari a 825,47 cm³ si po' adottare un profilo IPE 360 con modulo di resistenza pari a 904 cm³

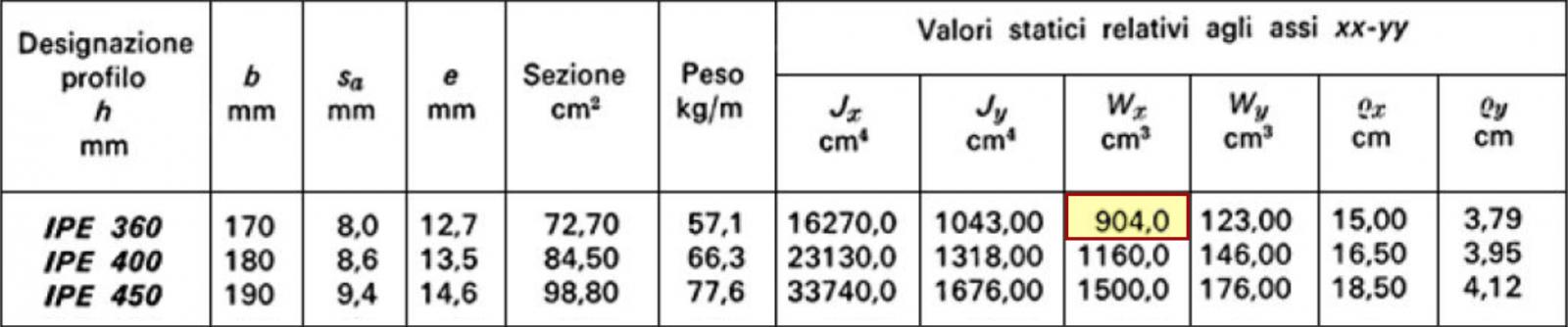
.06

Avendo inizialmente tralasciato nell'analisi dei carichi il peso proprio della trave, si può adesso ovviare alla mancanza ricavandosi il suo peso e aggiungendolo ai carichi agenti sulla struttura, ricordando che anche in questo caso il valore va moltiplicato per il coefficiente di sicurezza 1,3 (ma non per l'interasse).

Trave IPE 360 (Area = 72,7 cm²): 0,00727m³/m² x 78,5 kN/m³ = 0,571 kN/m²

Q_tot = 43,8656 + (1,3 x 0,571) = 44,6079 kN/m

.07

Come si evince dalla fig.07 il nuovo W_x rimane sempre al di sotto dei 904 cm³ del modulo di resistenza dell'IPE 360. Tale profilo risulta pertanto idoneo.

Solaio in LEGNO 

.08

Il solaio ligneo preso in esame è così composto:

Pavimentazione in cotto spessa 2 cm con un peso pari a 0,4 kN/m²

Sottofondo in cls alleggerito spesso 3 cm con un peso specifico di 18 kN/m³

Isolante in fibre di legno pressate spesso 4 cm con un peso specifico di 0,5 kN/m³

Caldana in cls spessa 4 cm con un peso specifico di 25 kN/m³ 

Tavolato in olmo spesso 3,5 cm con un peso 6 kN/m³

Travetti in olmo 10x15 cm e peso specifico di 6 kN/m³ 

Anche i questo caso si procede con l'analisi dei carichi suddividendoli in carichi strutturali, permanenti non strutturali e accidentali.

Carichi strutturali (q_s):

- 2 Travetti in olmo: 2 x 0,015 m³/m² x 6 kN/m³ = 0,18 kN/m²

- Tavolato in pioppo: 0,035 m³/m² x 6 kN/m³ = 0,21 kN/m²

Q_stot= 0,39 kN/m²

Carichi permanenti (q_p):

- Pavimentazione in cotto: 0,4 kN/m²

- Sottofondo in cls alleggerito: 0,03 m³/m² x 18 kN/m³ = 0,54 kN/m²

- Isolante in fibre di legno pressate: 0,04 m³/m² x 0,5 kN/m³ = 0,02 kN/m²

- Caldana in cls: 0,04 m³/m² x 25 kN/m³ = 1 kN/m²

A questi carichi si aggiungono poi sempre:

- Tramezzi: 1 kN/m²

- Impianti: 0,5 kN/m²

Q_Ptot= 3,46 kN/m²

Carichi accidentali (q_a)

Si prende nuovamente un carico accidentale pari a 2 kN/m².

Si inseriscono quindi i valori ottenuti nella tabella excel che provvederà a moltiplicare ciascun carico per il proprio coefficiente di sicurezza, a restituire il carico complessivo e, tenendo in considerazione la luce di 6 m, a calcolare il momento agente. 

Impostando ora come materiale per la trave un legno lamellare GL24H con resistenza a flessione caratteristica pari a 24 Mpa, si fissa una base di 30 cm e si ricava un altezza minima.

.09

Essendo necessaria un'altezza minima della trave pari a 46,65 cm, si decide di adottare un sezione 30x50 cm.

Si calcola ora il peso proprio della trave al fine di verificarla

Trave in legno lamellare GL24H (Area = 1500 cm², Peso specifico = 3,8kN/m³): 0,15m³/m² x 3,8 kN/m³ = 0,57 kN/m²

Q_tot = 32,02 + (1,3 x 0,57) = 32,761 kN/m

.10

L'altezza minima necessaria è inferiore a quella presa, quindi la trave risulta verificata anche al peso proprio.

Solaio in CLS ARMATO

.11

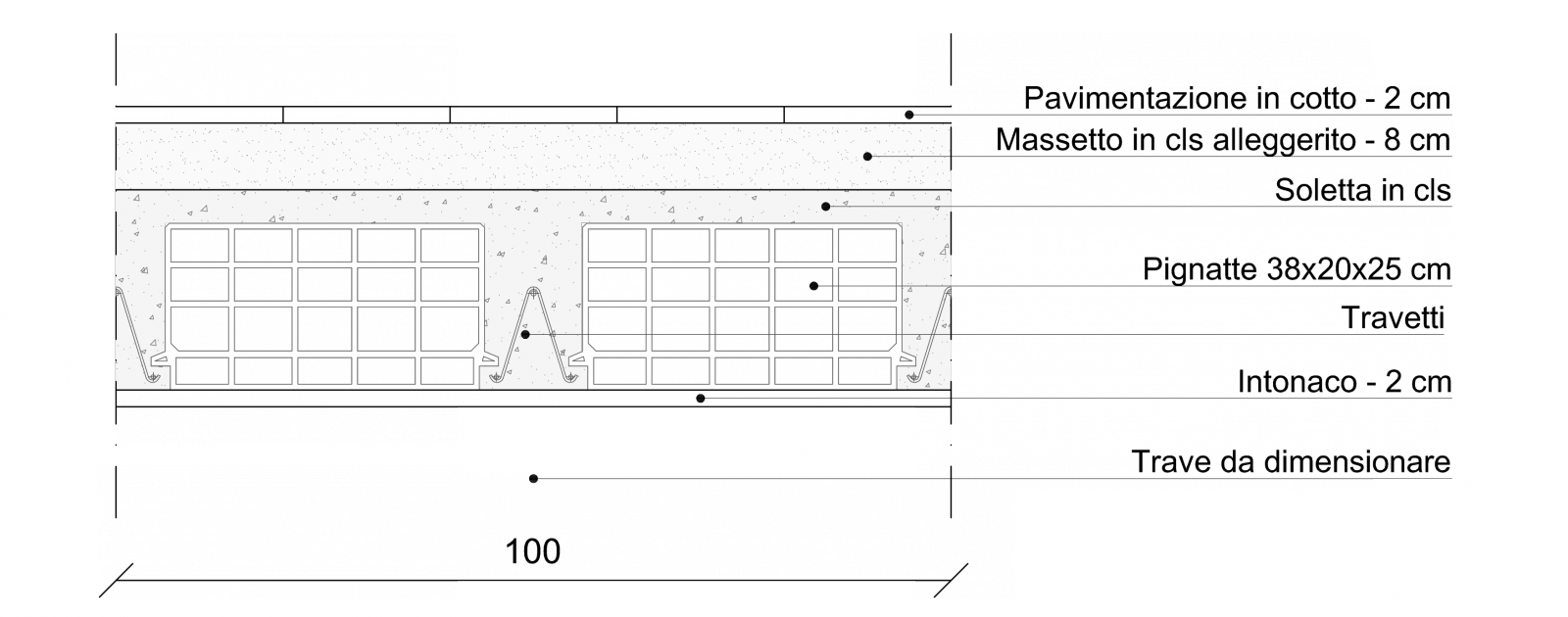
Concludo il mio studio analizzando un solaio in laterocemento così composto:

Pavimentazione in cotto spessa 2 cm con un peso pari a 0,4 kN/m²

Massetto in cls alleggerito spesso 8 cm con un peso specifico di 18 kN/m³

Soletta in cls spesso 4cm con un peso specifico di 25 kN/m³ 

Travetti 12x20 cm con un peso specifico di 25 kN/m³ 

Pignatte 38x20x25 cm (fig.12) dal peso di 0,096 kN l'una

Intonaco spesso 2 cm con peso specifico di 18 kN/m³ 

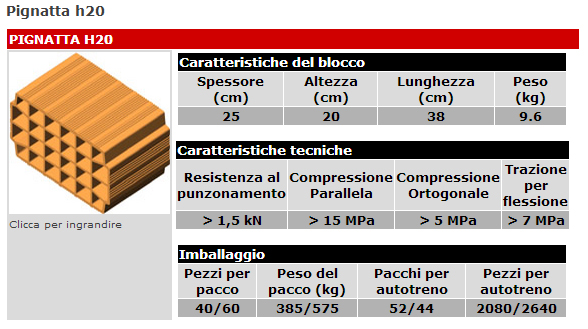
.12

Si procede con l'analisi dei carichi suddividendoli in carichi strutturali, permanenti non strutturali e accidentali.

Carichi strutturali (q_s):

- 2 Travetti in cls armato: 2 x (0,012 x 0,2 x 1) m³/m² x 25 kN/m³ = 1,2 kN/m²

- Soletta in cls armato: 0,04 m³/m² x 25 kN/m³ = 1 kN/m²

Per calcolarsi l'incidenza delle pignatte si deve prima fare un calcolo di quante ce ne sono in un m². In questo caso in ogni metro² si avranno due file di pignatte nel senso dei travetti, ciascuna composta da 4 elementi, per un totale di 8 pignatte al m². 

- Pignatte: 8 m^-2 x 0,096 kN = 0,768 kN/m²

Q_stot= 2,968 kN/m²

Carichi permanenti (q_p):

- Pavimentazione in cotto: 0,4 kN/m²

- Sottofondo in cls alleggerito: 0,08 m³/m² x 18 kN/m³ = 1,44 kN/m²

- Intonaco: 0,02 m³/m² x 18 kN/m³ = 0,36 kN/m²

A questi carichi si aggiungono poi:

- Tramezzi: 1 kN/m²

- Impianti: 0,5 kN/m²

Q_Ptot= 3,7 kN/m²

Carichi accidentali (q_a)

Anche in questo caso si prende un carico accidentale pari a 2 kN/m²

Prima di riprendere in mano il foglio excel, sarà necessario definire le caratteristiche della trave da progettare. Si opta per dei ferri di armatura B450C (fyk = 450 MPa), un calcestruzzo ordinario C35/45 (fck=35MPa, Rck=45Mpa), una base della trave di 25 cm e un copriferro di 5 cm.

Si procede dunque a tabellare i dati.

.13

Osservando la tabella si può notare che, non tenendo conto del peso proprio della trave si potrebbe optare per una sezione rettangolare 25x45, in quanto l'altezza minima richiesta è di 44,95 cm. Essendo però un valore così vicino al limite la sezione sicuramente non risulterebbe verificata aggiungendo il peso della trave. Si decide quindi di adottare un profilo 25x50. 

Si calcola il peso della trave:

(0,25 x 0,5 x 1) m³/m² x 25 kN/m³ =  3,125 kN/m²

Aggiungendolo ai carichi precedentemente determinati:

Q_tot = 46,6736 + (1,3 x 3,125) = 50,7361 kN/m

.13

La sezione adottata risulta anche in questo caso verificata.

Se si volesse definire una travatura reticolare nel modo più semplice possibile, sarebbe sufficiente descriverla come un insieme di aste collegate mediante cerniere. Questo fa capire come spesso sono proprio gli elementi più semplici che, declinati nel modo corretto, permettono la maggior libertà creativa e costruttiva. Sì, perchè le travature reticolari di libertà ne garantiscono molta, basti pensare a come una successione di aste rettilinee possa dar origine ad una grande copertura ondulata, libera espressione di un'idea progettuale, permettendo inoltre di coprire enormi luci riducendo al minimo i punti di scarico (fig.01). 

.01

Con questo ovviamente non si vuol dire che sia una cosa "elementare" progettare una copertura di questo tipo, i vincoli di cui bisogna tenere conto e i calcoli che vi sono alle spalle sono molti, ma essenzialmente che il suo  funzionamento, riducendo a zero il momento e il taglio, grazie alle aste incernierate, e permettendo di concentrarsi solo sullo sforzo assiale dei tiranti (aste tese) e puntoni (aste compresse), è sicuramente più semplice.

Arrivo quindi a cercare di spiegare come mediante l'uso di alcuni programmi appositi, sia possibile progettare e studiare il funzionamente di una copertura reticolare. 

Anzitutto si deve disegnare la struttura da analizzare, operazione che si può svolgere o usando un programma di modellazione 3D quali Autocad 3D o Rhinoceros o in alternativa ricreando direttamente il modello nel programma di analisi Sap2000.

Prendendo liberamente spunto da alcune tipiche coperture di impianti sportivi io ho iniziato a dare vita tramite il programma di modellazione 3d Rhinoceros alla copertura in figura .02

.02

Si procede quindi ad importarla nel vero programma di studio Sap2000 (fig .03) prestando attenzione a riunire i margini che potrebbero essersi corrotti durante l'importazione (fig.04).

Si aggiungono quindi dei vincoli alla struttura, nel mio caso delle cerniere.

A questo punto abbiamo la nostra struttura nel programma. Per renderla però effettivamente reticolare bisogna prima "liberare" i momenti dai nodi trasformandoli in cerniere interne. Sap2000 infatti riconosce le unioni delle aste come incastri. Per farlo basta selezionare l'intera struttura, andare su Assign> Frame> Releases/Partial Fixity, quindi rilasciare i momenti (fig.07). 

Si procede poi col definire dei carichi puntuali (tralasciando per il momento il peso proprio della trave - fig.09), assegnando un valore in KN negativo lungo l'asse z (fig.10).

Si ipotizza quindi una distribuzione di tali carichi sui nodi nella parte centrale della struttura (fig.11-12).Ultima cosa da fare prima di compiere l'analisi è quellla di assegnare alle aste una geometria e un materiale. Si procede nuovamente a selezionare l'intera struttura, quindi andando su Assing> Frame> Frame Sections si crea una nuova sezione indicandone la forma e il materiale. Nel mio caso ho scelto una sezione tubolare in acciaio (fig.13).

Si può quindi procedere con l'analisi premendo il tasto Run Analysis selezionando i carichi di cui si vuol tenere conto (fig.15).

Appare immediatamente la deformata della struttura. Come si può evincere dalla fig.16 la parte della struttura che subisce maggiori deformazioni è quella soggetta direttamente ai carichi.

Selezionando Show Forces/Stresses> Joints Sap2000 permette di vedere le reazioni vincolari delle cerniere imposte.

  Selezionando invece  Show Forces/Stresses> Frame/Cables si potrà scegliere di visualizzare le sollecitazioni interne. Nel case di travi reticolari si visualizzerà solo lo sforzo assiale (fig.19-20)

Una volta ottenuti i grafici dello Sforzo Normale potrebbe risultare utile avere tabellati tutti i valori trovati. Si può dunque procedere ad esportare l'analisi in un foglio di calcolo come Excel (fig.21). 

Si ottiene quindi una tabella che riassume l'analisi effettuata.

Si può facilmente riscontrare che sia il Taglio che il Momento risultano in ogni asta pari a 0 (risultato concorde con la natura reticolare della struttura), mentre lo Sforzo Normale varia tra valori negativi (aste compresse) e positivi (aste tese). Nello specifico si può notare che le aste più compresse (fig.22) sono situate nella parte centrale del corrente superiore, le aste più tese in quello inferiore (fig.23), mentre le aste minormente sollecitate (sebbene non ve ne siano di completamente scariche) si trovano in prossimità del cambio di curvatura della struttura.