Esercitazione 1 - Copertura reticolare 3D

Se si volesse definire una travatura reticolare nel modo più semplice possibile, sarebbe sufficiente descriverla come un insieme di aste collegate mediante cerniere. Questo fa capire come spesso sono proprio gli elementi più semplici che, declinati nel modo corretto, permettono la maggior libertà creativa e costruttiva. Sì, perchè le travature reticolari di libertà ne garantiscono molta, basti pensare a come una successione di aste rettilinee possa dar origine ad una grande copertura ondulata, libera espressione di un'idea progettuale, permettendo inoltre di coprire enormi luci riducendo al minimo i punti di scarico (fig.01). 

.01

Con questo ovviamente non si vuol dire che sia una cosa "elementare" progettare una copertura di questo tipo, i vincoli di cui bisogna tenere conto e i calcoli che vi sono alle spalle sono molti, ma essenzialmente che il suo  funzionamento, riducendo a zero il momento e il taglio, grazie alle aste incernierate, e permettendo di concentrarsi solo sullo sforzo assiale dei tiranti (aste tese) e puntoni (aste compresse), è sicuramente più semplice.

Arrivo quindi a cercare di spiegare come mediante l'uso di alcuni programmi appositi, sia possibile progettare e studiare il funzionamente di una copertura reticolare. 

Anzitutto si deve disegnare la struttura da analizzare, operazione che si può svolgere o usando un programma di modellazione 3D quali Autocad 3D o Rhinoceros o in alternativa ricreando direttamente il modello nel programma di analisi Sap2000.

Prendendo liberamente spunto da alcune tipiche coperture di impianti sportivi io ho iniziato a dare vita tramite il programma di modellazione 3d Rhinoceros alla copertura in figura .02

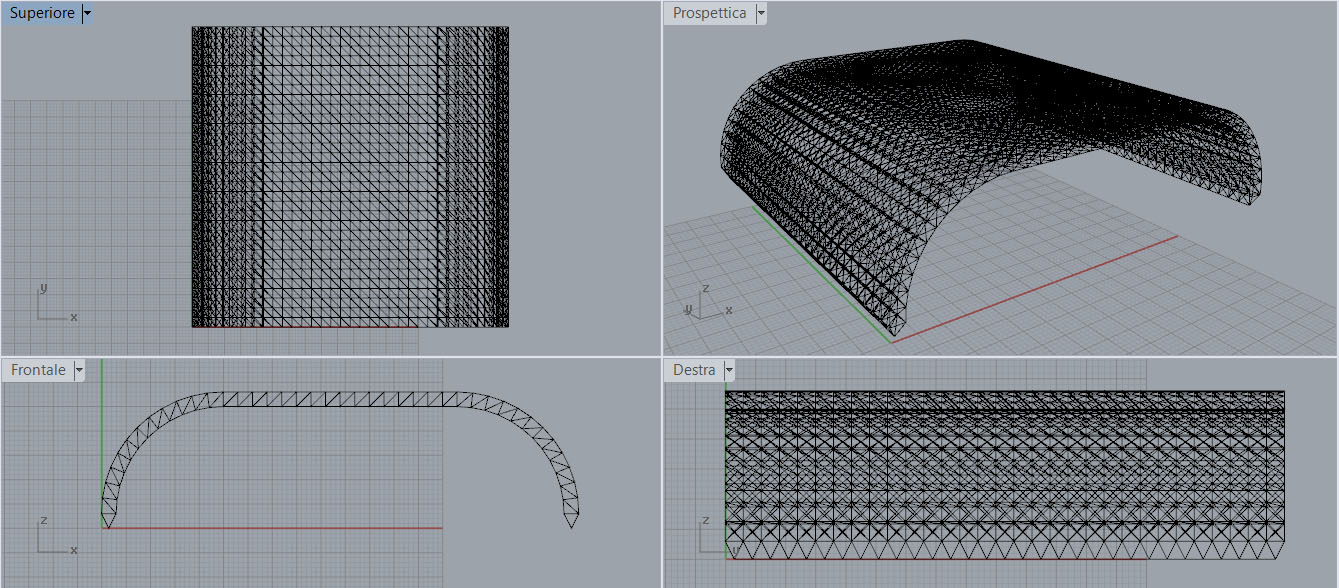
.02

Si procede quindi ad importarla nel vero programma di studio Sap2000 (fig .03) prestando attenzione a riunire i margini che potrebbero essersi corrotti durante l'importazione (fig.04).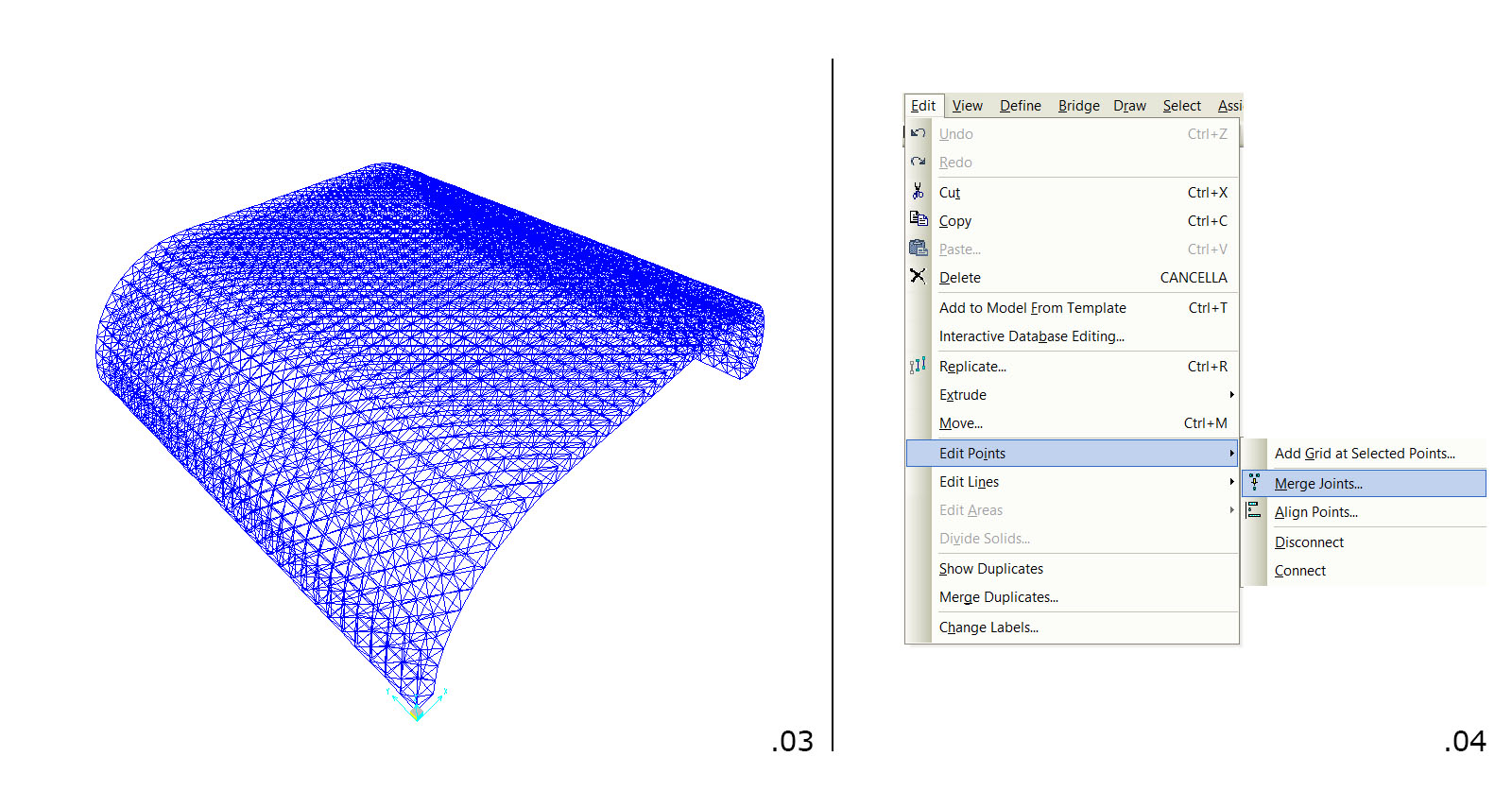

Si aggiungono quindi dei vincoli alla struttura, nel mio caso delle cerniere.

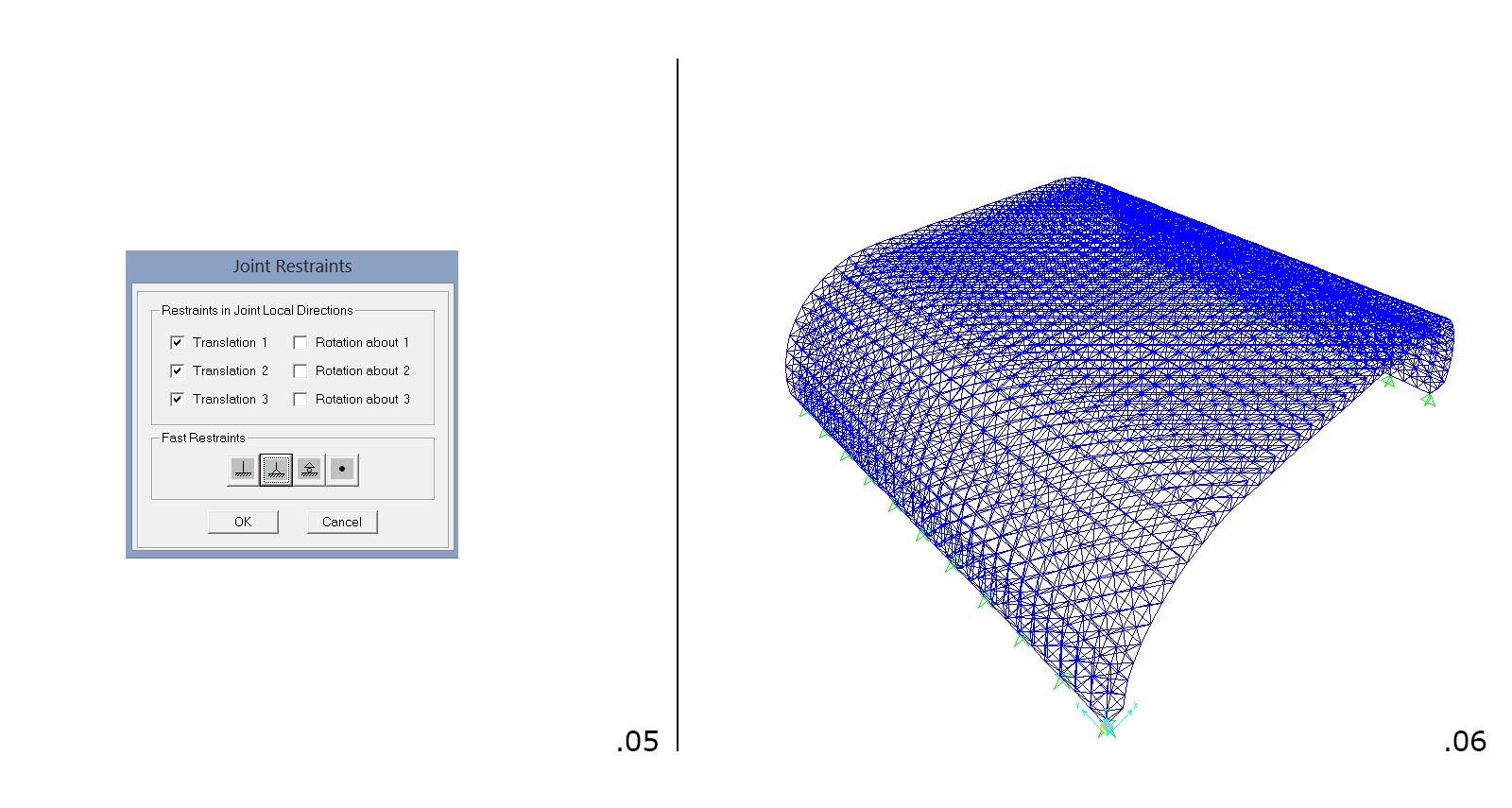
A questo punto abbiamo la nostra struttura nel programma. Per renderla però effettivamente reticolare bisogna prima "liberare" i momenti dai nodi trasformandoli in cerniere interne. Sap2000 infatti riconosce le unioni delle aste come incastri. Per farlo basta selezionare l'intera struttura, andare su Assign> Frame> Releases/Partial Fixity, quindi rilasciare i momenti (fig.07).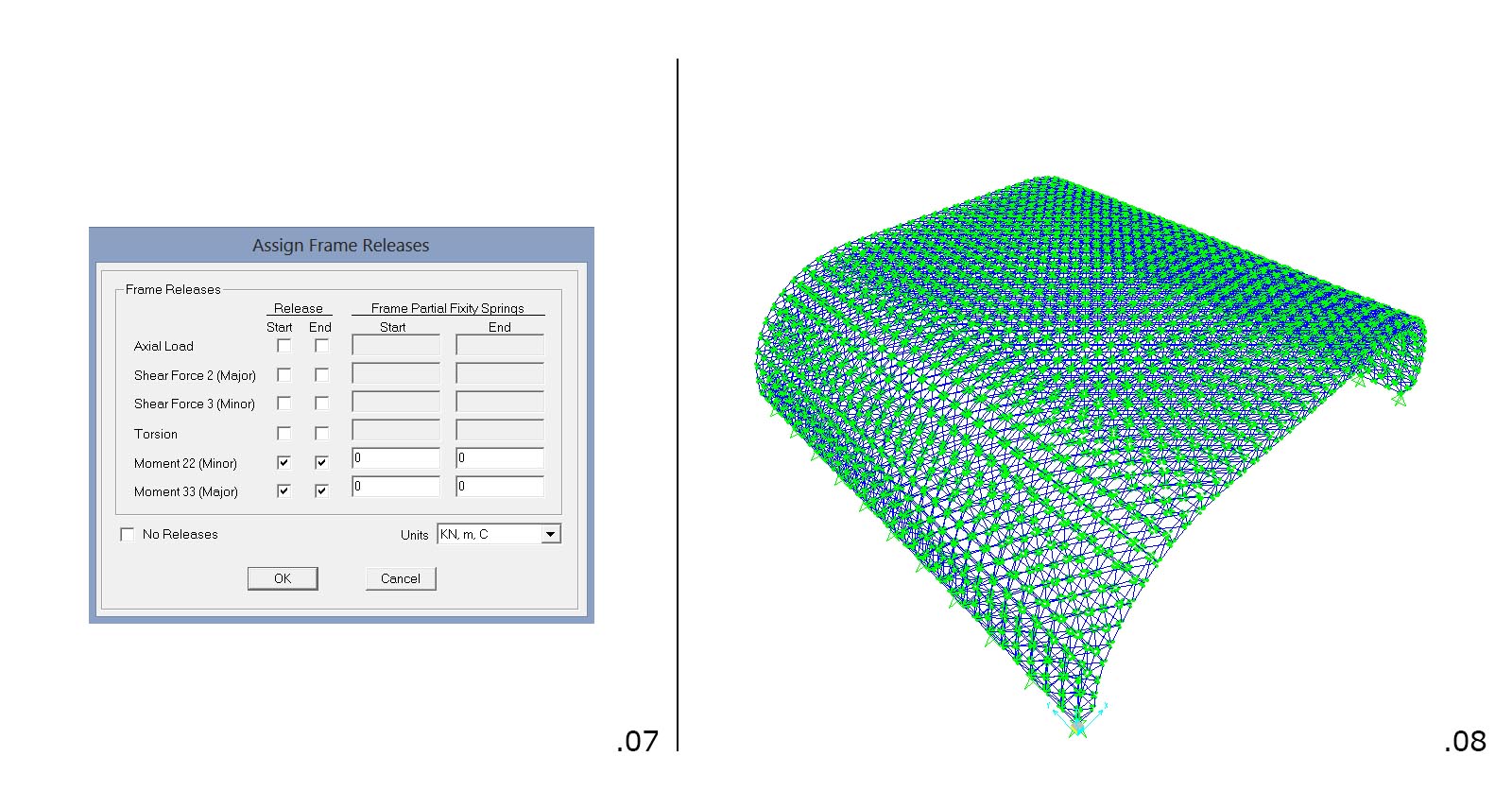 

Si procede poi col definire dei carichi puntuali (tralasciando per il momento il peso proprio della trave - fig.09), assegnando un valore in KN negativo lungo l'asse z (fig.10).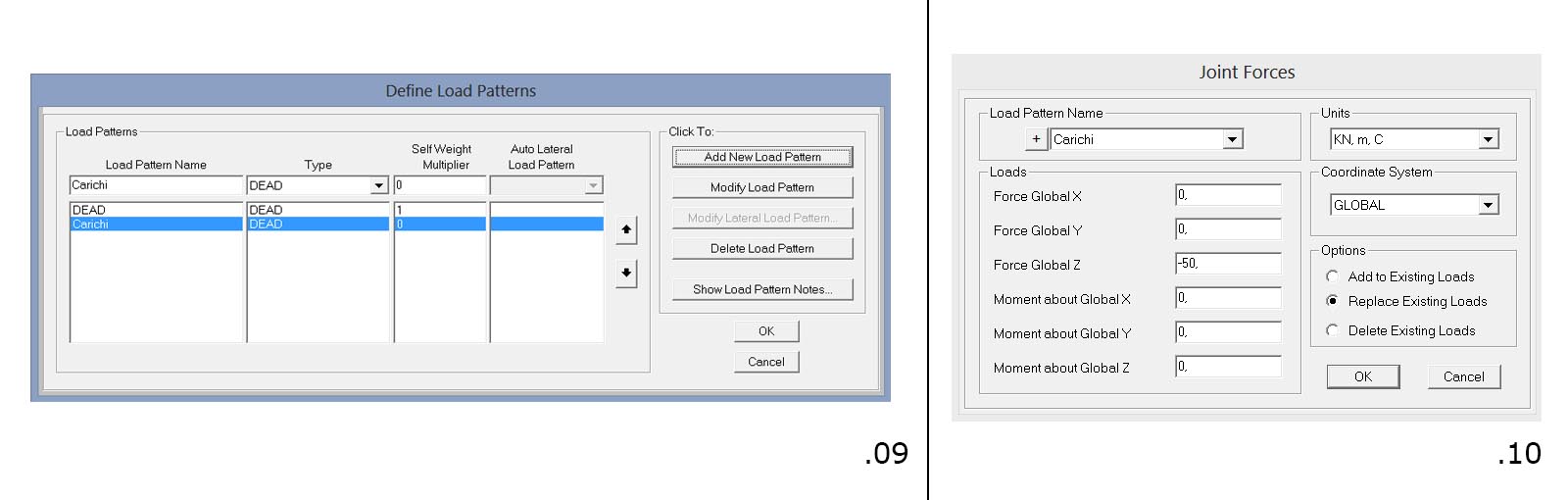

Si ipotizza quindi una distribuzione di tali carichi sui nodi nella parte centrale della struttura (fig.11-12).Ultima cosa da fare prima di compiere l'analisi è quellla di assegnare alle aste una geometria e un materiale. Si procede nuovamente a selezionare l'intera struttura, quindi andando su Assing> Frame> Frame Sections si crea una nuova sezione indicandone la forma e il materiale. Nel mio caso ho scelto una sezione tubolare in acciaio (fig.13).

Si può quindi procedere con l'analisi premendo il tasto Run Analysis selezionando i carichi di cui si vuol tenere conto (fig.15).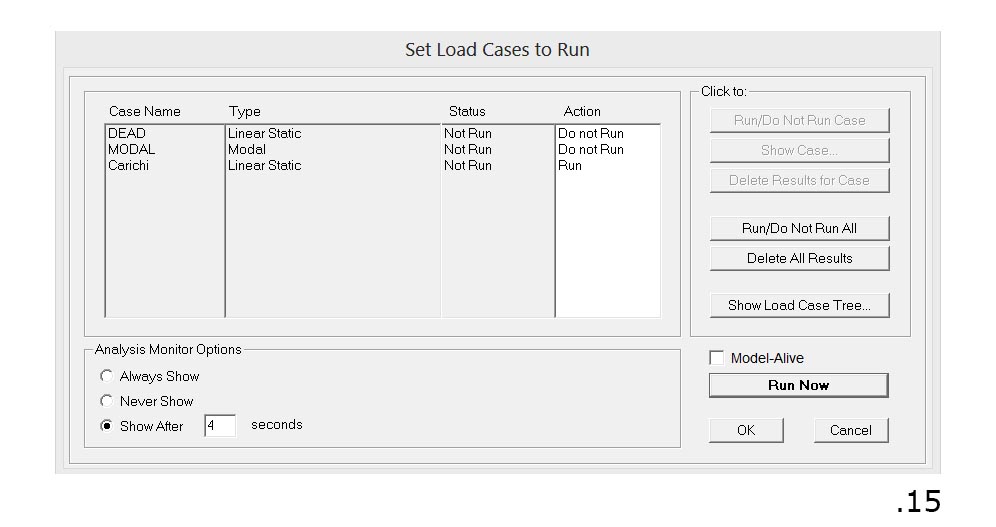

Appare immediatamente la deformata della struttura. Come si può evincere dalla fig.16 la parte della struttura che subisce maggiori deformazioni è quella soggetta direttamente ai carichi.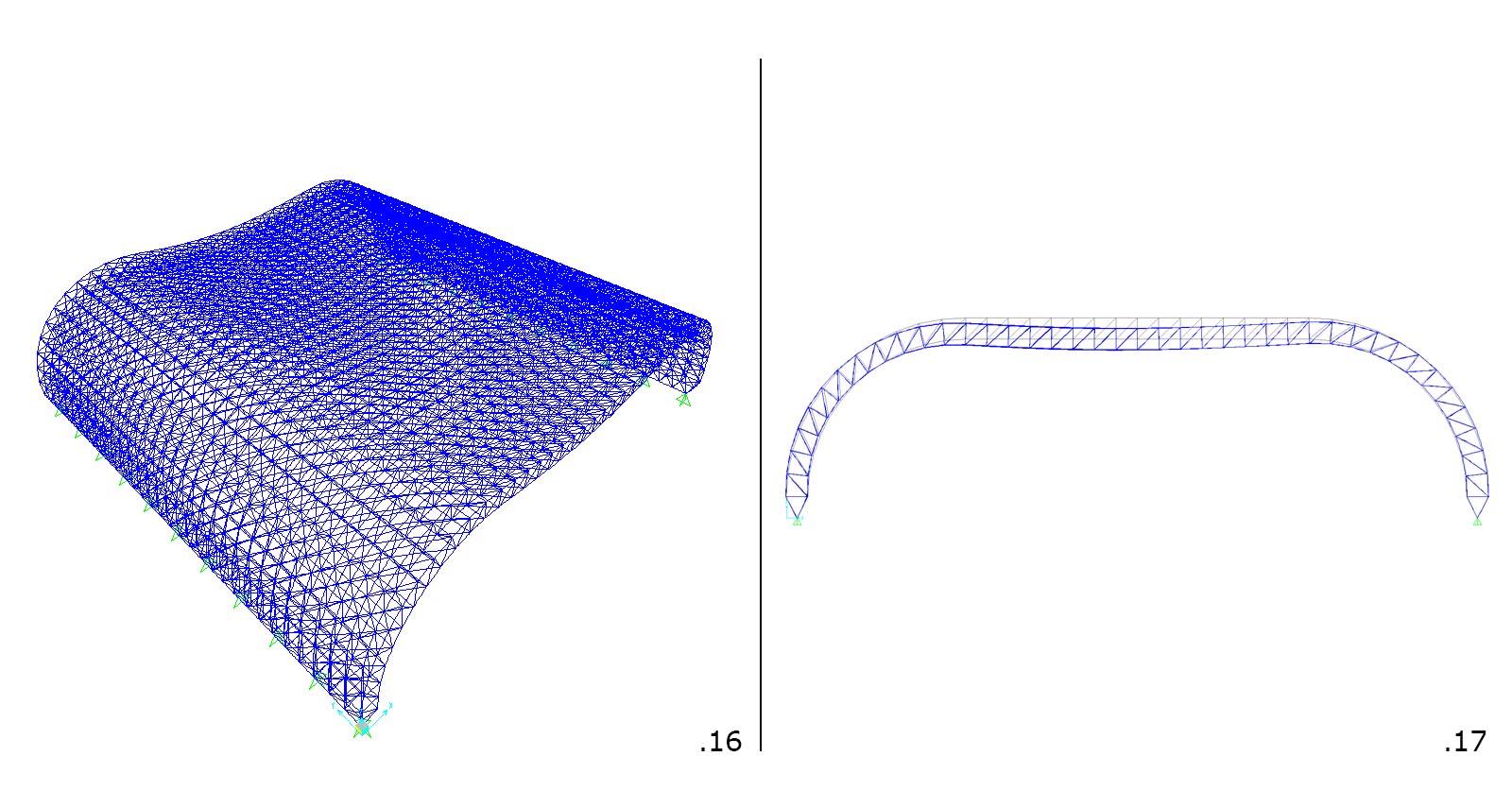

Selezionando Show Forces/Stresses> Joints Sap2000 permette di vedere le reazioni vincolari delle cerniere imposte.

  Selezionando invece  Show Forces/Stresses> Frame/Cables si potrà scegliere di visualizzare le sollecitazioni interne. Nel case di travi reticolari si visualizzerà solo lo sforzo assiale (fig.19-20)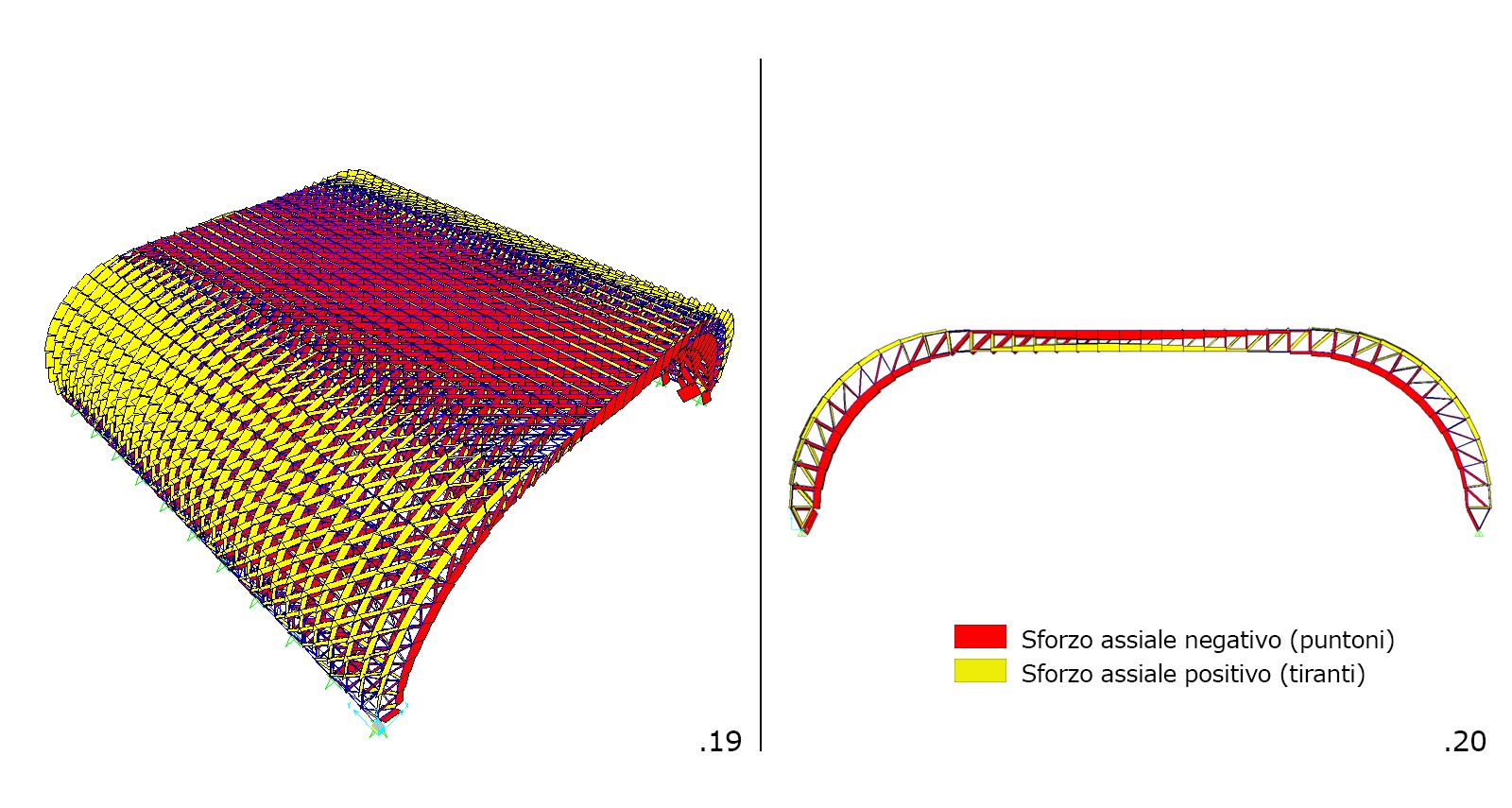

Una volta ottenuti i grafici dello Sforzo Normale potrebbe risultare utile avere tabellati tutti i valori trovati. Si può dunque procedere ad esportare l'analisi in un foglio di calcolo come Excel (fig.21).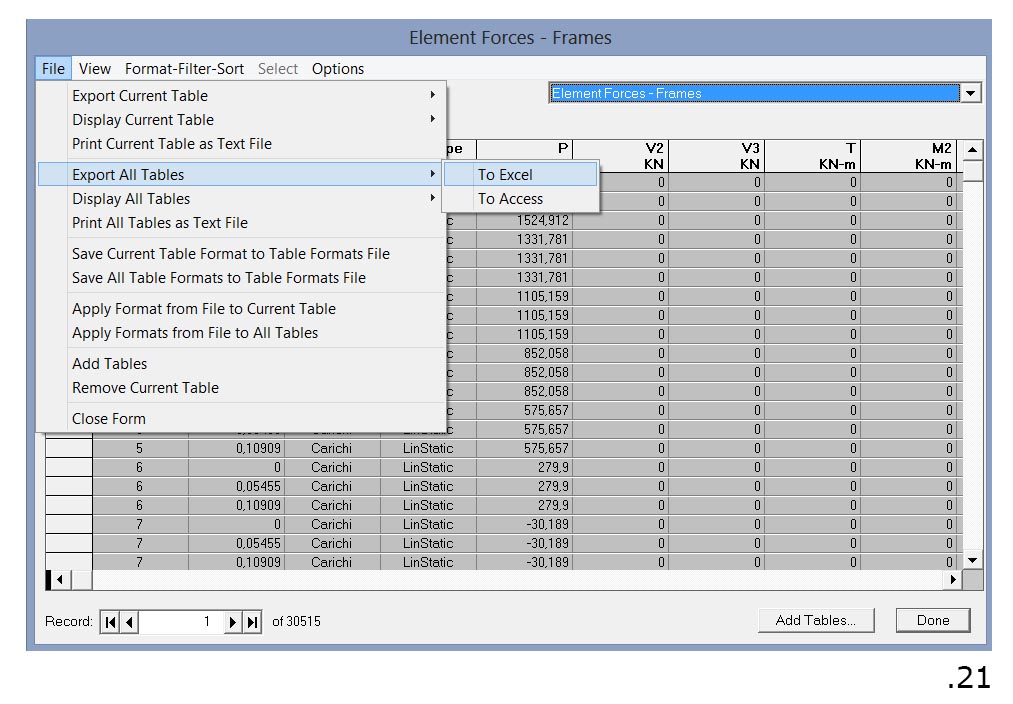 

Si ottiene quindi una tabella che riassume l'analisi effettuata.

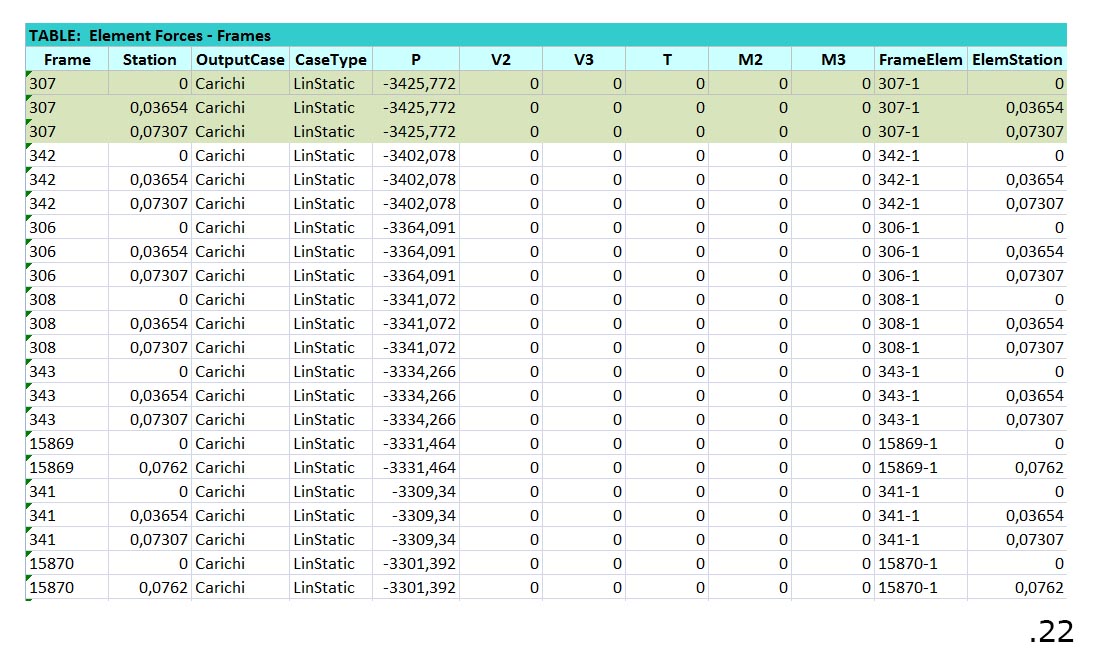
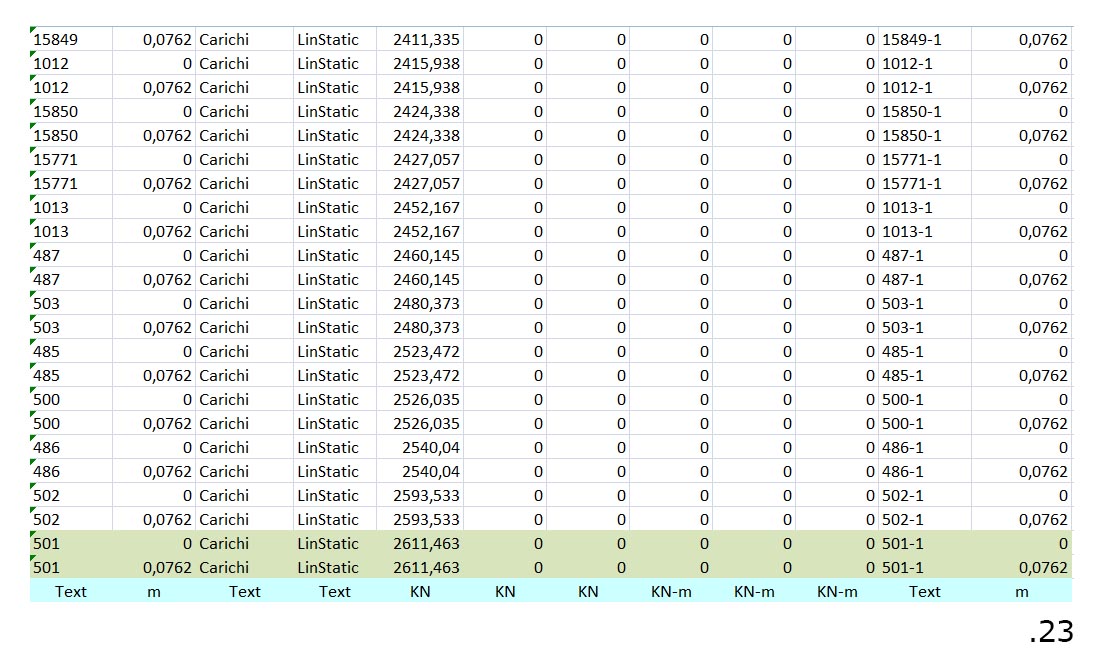
Si può facilmente riscontrare che sia il Taglio che il Momento risultano in ogni asta pari a 0 (risultato concorde con la natura reticolare della struttura), mentre lo Sforzo Normale varia tra valori negativi (aste compresse) e positivi (aste tese). Nello specifico si può notare che le aste più compresse (fig.22) sono situate nella parte centrale del corrente superiore, le aste più tese in quello inferiore (fig.23), mentre le aste minormente sollecitate (sebbene non ve ne siano di completamente scariche) si trovano in prossimità del cambio di curvatura della struttura.