blog di Sabrina Magliocchetti

In questa esercitazione si analizzerà la deformabilità di una trave a sbalzo in tre diversi materiali, in calcestruzzo armato, in legno e in acciaio. Si studia il telaio mostrato in figura sottostante, con interasse pari a 3 m e luce dello sbalzo pari a 3 m, in cui viene evidenziata la trave maggiormente sollecitata.

                                    Fig. 1

Per calcolare la deformabilità di una trave a sbalzo, come è stato fatto nell’esercitazione precedente della trave appoggiata, prima di tutto è necessario calcolare i carichi agenti su di essa.

SOLAIO IN CLS

                                    Fig. 2

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    2.13    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. E' inoltre necessario inserire il valore pari 450 MPa per la resistenza caratteristica delle armature e scegliendo una classe C 40/50 per il cls si definisce anche la resistenza caratteristica a compressione pari a 50 Mpa.

Infine si sceglie la base della trave pari a 30 cm e si ottine l'altezza.

L'altezza della trave risulta essere pari a 28.73 cm questo valore viene arrotondato a 35 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.35 m x 1 m ) x 25KN/m³ = 2.625 KN/m

l/Vmax>250 è verificata poiché l/Vmax =341 e si ha uno spostamento Vmax pari a 0.88 cm.

SOLAIO IN LEGNO

Fig. 3

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    1.2    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. Si è scelto un legno lamellare GL 24h con resistenza a flessione fm,k = 24MPa e la base della trave pari a 30cm.

Considerando la base della trave pari a 30 cm si ottiene un'altezza pari a 36.4 cm che si arrotonda a 40 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.40 m x 1 m ) x 7 KN/m³ = 0.84 KN/m

l/Vmax>250 è verificata poiché l/Vmax =265 e si ha uno spostamento Vmax pari a 1.13 cm.

SOLAIO IN ACCIAIO

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    1    Kn/ m²

Carichi permanenti qp=  1   KN/m²

Carichi accidentali qa=    2   KN/m²

Per dimensionare una trave in acciaio, una volta che si conosce la Wx è possibile ricavare la sezione dal profilario.

Quindi si sceglie una IPE 220 con una Wx=252 cm³ e Ix= 9110 cm⁴ .

Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

P= (0.0033 m² x 1m)/m x 78,50 KN/m³= 0.259 KN/m

l/Vmax>250 è verificata poiché l/Vmax =374 e si ha uno spostamento Vmax pari a 0.8 cm.

In tutte le tecnologie considerate nel caso in cui la verifica non fosse stata soddisfatta si sarebbe dovuta modificare la sezione oppure la luce.

Per poter dimensionare la trave più sollecitata del solaio rappresentato in fig.1 è necessario individuare le azioni agenti su di esso.

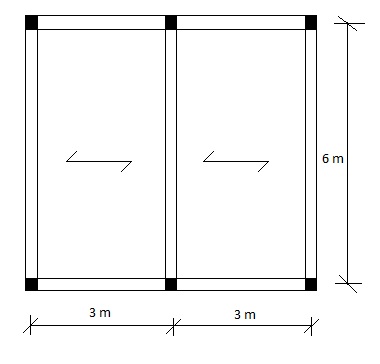
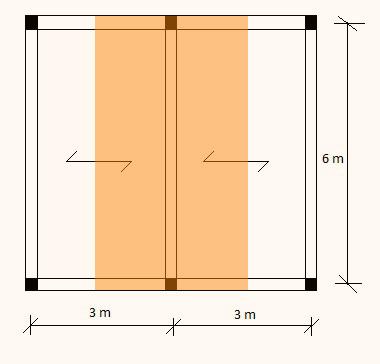              Fig.1

Le azioni si classificano secondo la loro durata e possono essere permanenti o variabili, quelle permanenti sono le azioni che permangono per tutta la vita utile della struttura.

Le azioni permanenti a loro volta si suddividono in portanti e non portanti, le prime sono legate al peso proprio del materiale le seconde individuano opere non strutturali ma fisse.

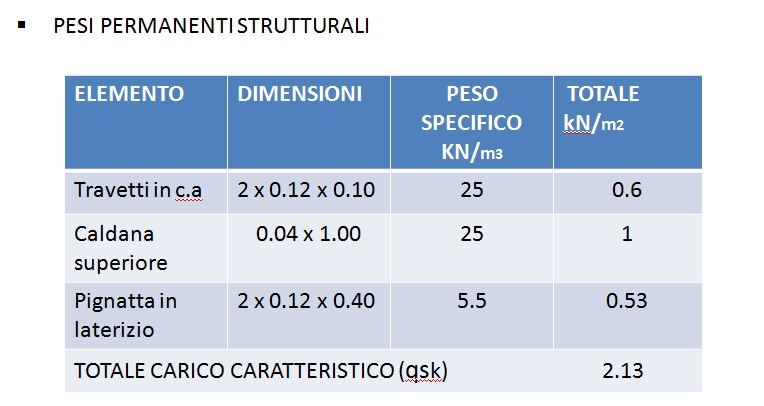
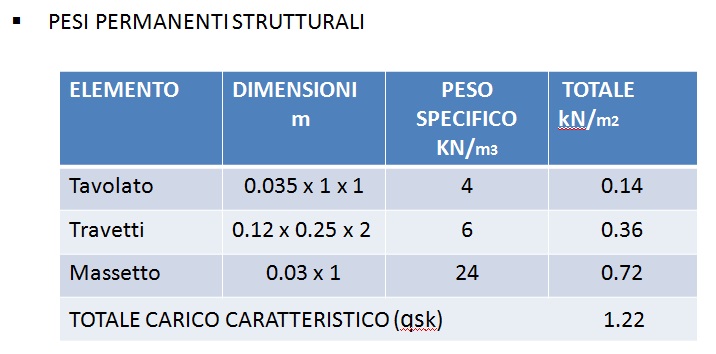
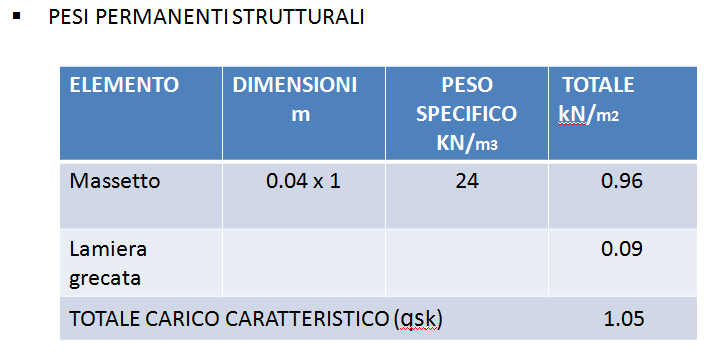
Si determinano in seguito i pesi permanenti strutturali di un metro quadrato di solaio rappresentato in fig.2

SOLAIO IN CLS

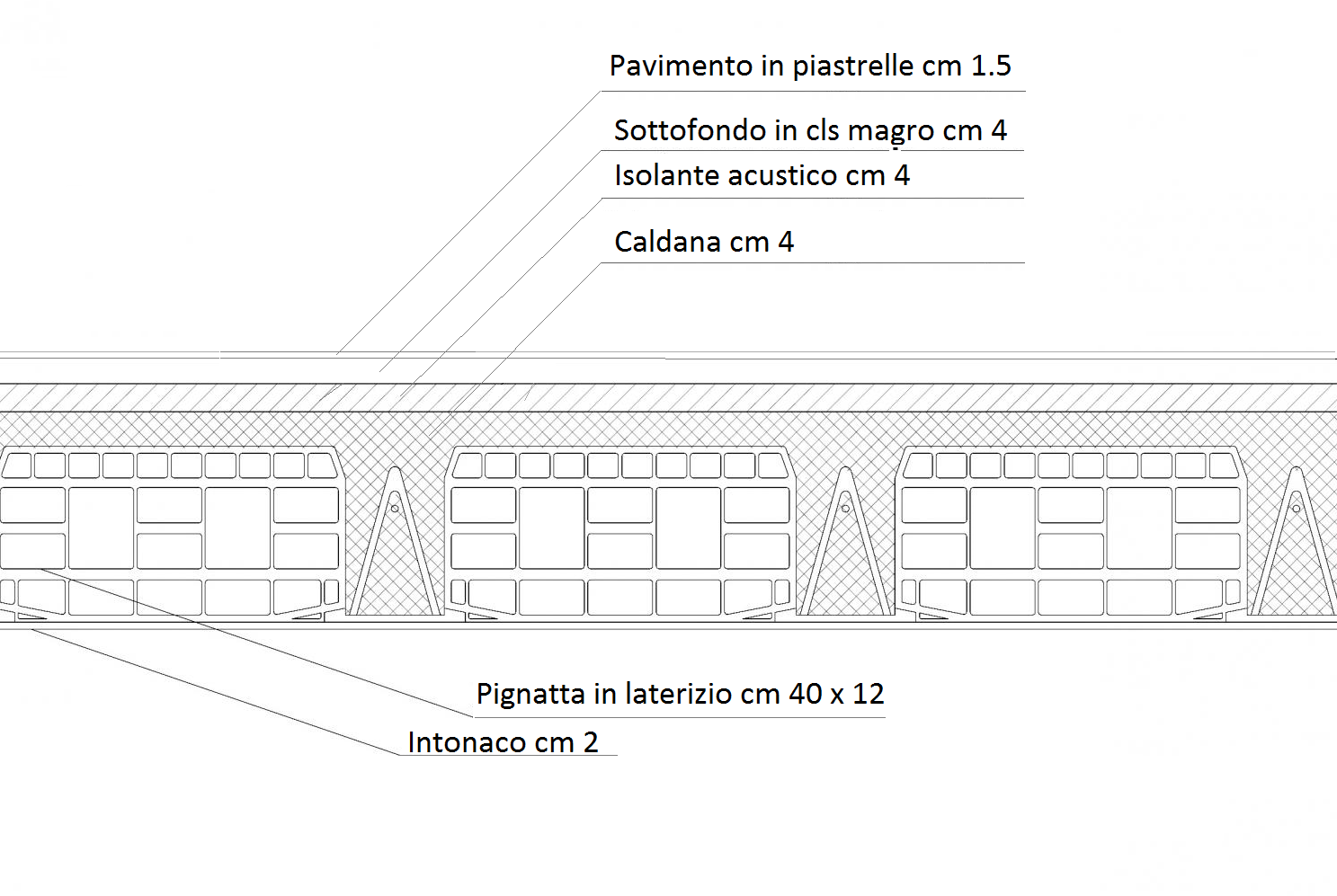
                                        Fig.2

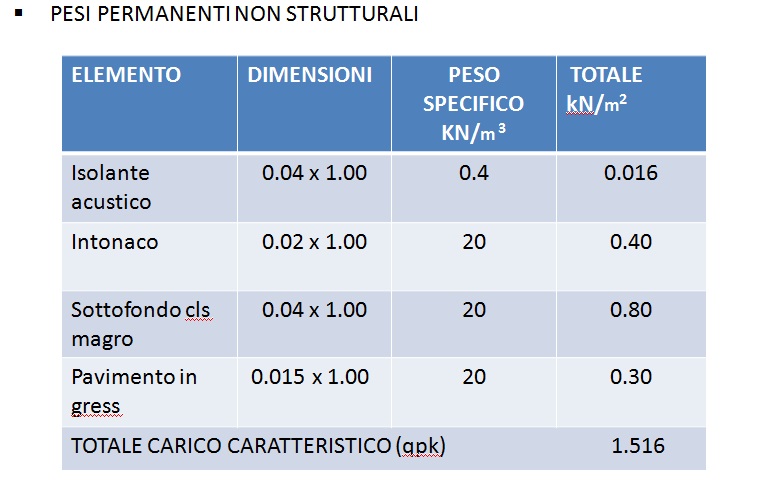
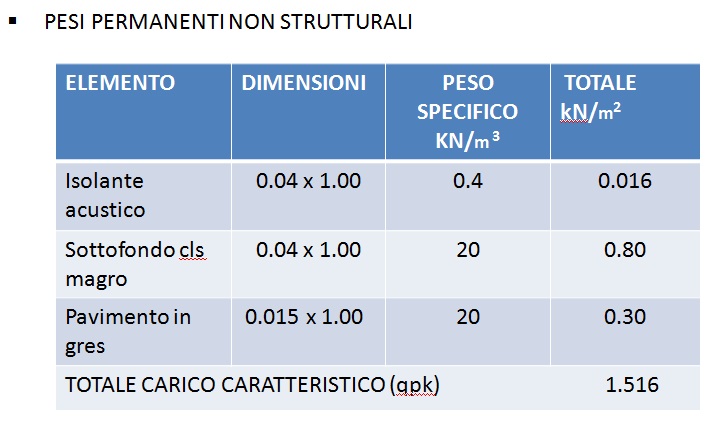
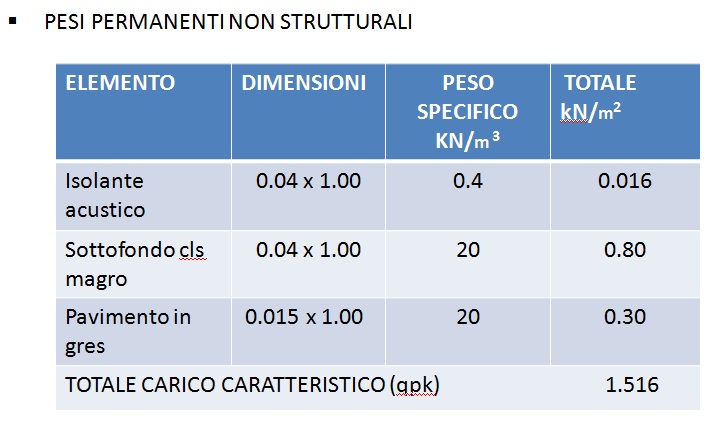
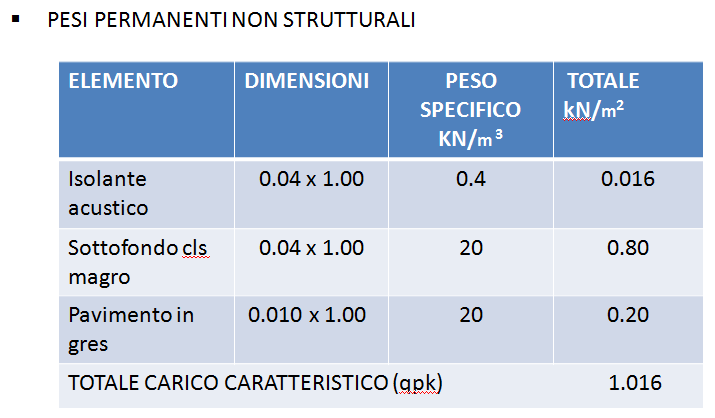
Nelle seguenti tabelle vengono individuati i due carichi qsk e qpk.

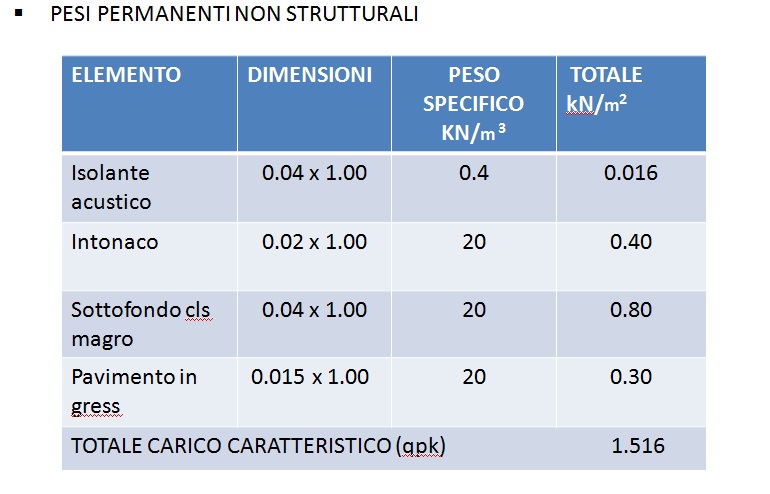
Le azioni variabili possono mutare in virtù della destinazione d’uso a seconda del luogo e delle condizioni ambientali stagionali.

In questo caso considerando una destinazione di tipo residenziale il carico variabile, dato dalla normativa, è pari a 2.00 KN/ m²_.

              qa = 2.00 KN/m²

Ora è possibile riportare i risultati ottenuti dal calcolo dei carichi nella tabella excel.

Nella tabella si applica un coefficiente di combinazione dei carichi, per quelli permanenti strutturali è pari a 1.3 ,  per i permanenti non strutturali e per i variabili pari a 1.5, inoltre viene considerata la fascia di influenza  per la trave più caricata.

Nel caso preso in considerazione la trave più sollecitata è quella evidenziata in fig.1 , l’area della fascia di influenza è quindi data da 3 x 6 = 18 mq, considerando 3 m come interasse  e 6 m come luce.

In celeste sono evidenziati i valori che vanno introdotti nella tabella per poter ottenere il dimensionamento della trave, oltre ai carichi e alle luci descritti precedentemente, è necessario scegliere e inserire il valori di Fyk (resistenza caratteristica dell’acciaio da armatura) pari a 450 MPa e Rck (resistenza caratteristica cubica) pari a 40 MPa, infine si decide la misura della base della trave a seconda delle necessità di progetto.

Scegliendo come base una misura pari a 25 cm l’altezza, come osservabile in tabella sarà pari a 35.60 cm che si arrotondano per eccesso a 40 cm.

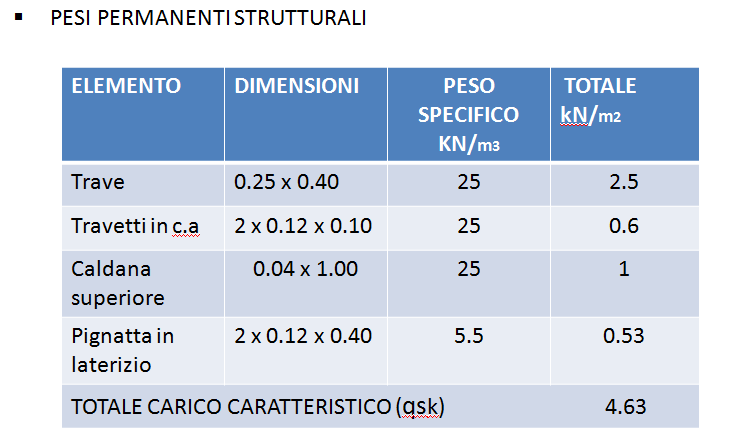
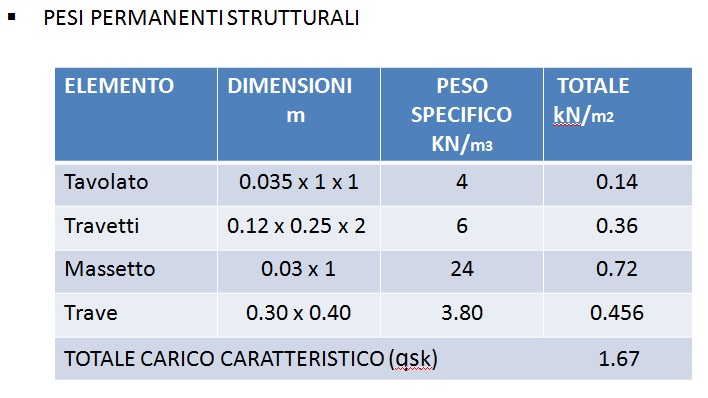
Viene quindi ricalcolato il peso della trave 25 x 40 che è pari a 2.50 KN/m come mostrato in tabella.

Nel calcolo dei carichi non è stato considerato il peso peroprio della trave,  che quindi viene ora preso in considerazione. Questo si ottiene moltiplicando l'area della trave per il peso specifico del materiale di cui è composta. Questo nuovo carico va aggiunto ai carichi strutturali per poter poi valutare la resistenza della trave.

Peso Trave = 0.25 x 0.40 x 25 KN/m³ = 2.5 KN/m²

Dove 25 kN/m³ è il peso specifico del calcestruzzo.

Si ricalcolano i carichi considerando ora il peso della trave.

     q = qsk x γ_s + qpk x γ_p + qa x γ_A

Si ricalcola il momento massimo M_max = ql²/8       M_max= 32.90 x 6²/ 8 = 148

Si può notare che l'altezza della trave calcolata con il peso della trave risulta seperiore a quello precedentemente calcolato nel predimensionamento, quindi non è sufficiente una trave 25 x 40 poiché il momento massimo da 104 KN x m è aumentato a 148 KN x m.

SOLAIO IN LEGNO

Con lo stesso criterio con cui sono stati ricavati i carichi per un solaio in calcestruzzo armato si individuano i carichi per un solaio in legno strutturato come in figura 3. e con le luci del solaio in figura1.

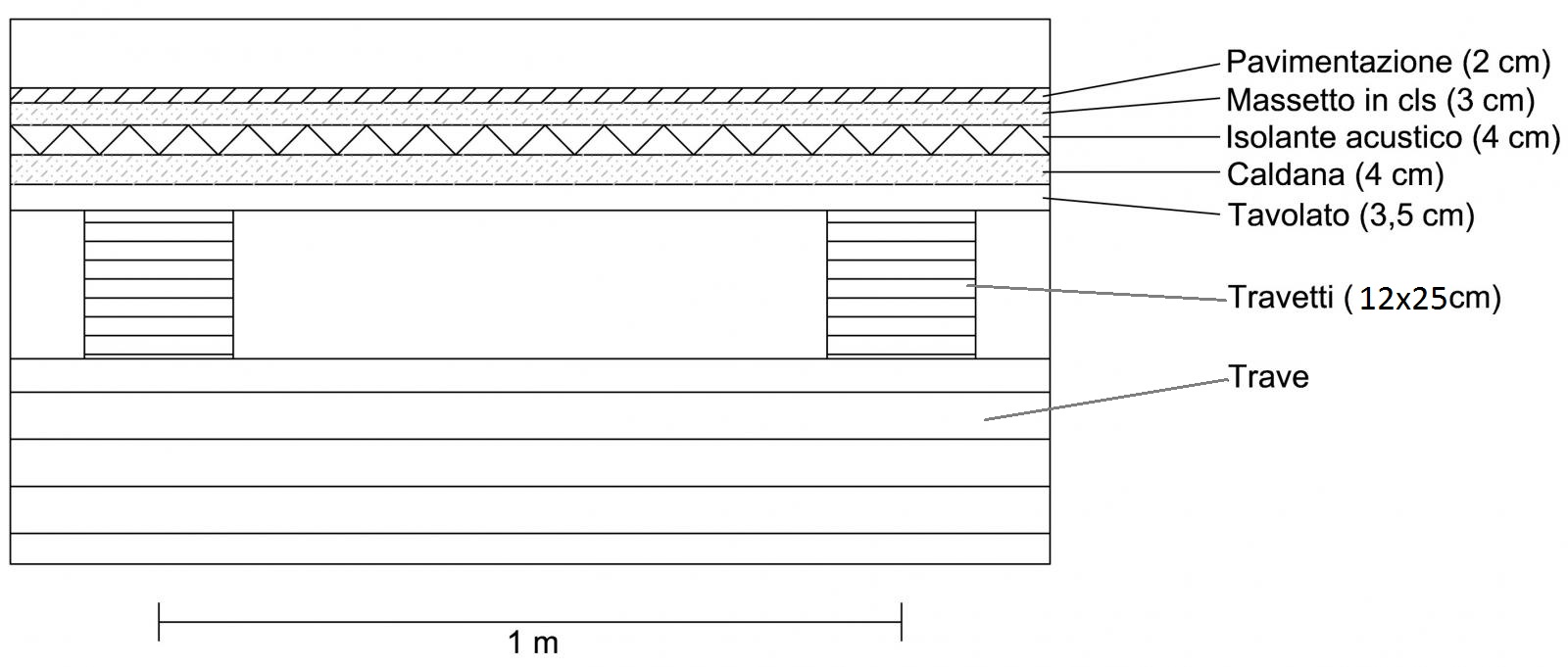Fig.3

          qa = 2.00 KN/m²  

Inserendo i carichi trovati nella tabella excel è possibile predimensionare la trave del solaio in legno.

Si imposta una base di 30 cm e si ottiene un'altezza di 36 cm che varra arrotodata a 40 cm. 

Il momento massimo è pari a 88.2 KN/m² .

Per verificare il dimensionamento è necessario inserire all’interno del calcolo dei carichi il peso proprio della trave proprio come è stato fatto precedentemente con il solaio in cls.

E' stato scelto un legno lamellare GL 24 h con un peso specifico di 3,80 KN/m³.

       qa = 2.00 KN/m²  

Attraverso l'ausilio delle tabelle excel è possibile verificare il dimensionamento fatto inserendo il nuovo carico permanente strutturale che tiene conto del peso della trave.

E' possibile notare dalla tabella excel che introducendo il nuovo carico qs il momento massimo cambia da 88.2 KNxm a 96.1 KNxm  e l'altezza della trave è ora di 38 cm era stata predimensionata un'altezza di 40 cm quindi il dimensionamento in questo caso è stato verificato.

SOLAIO IN ACCIAIO

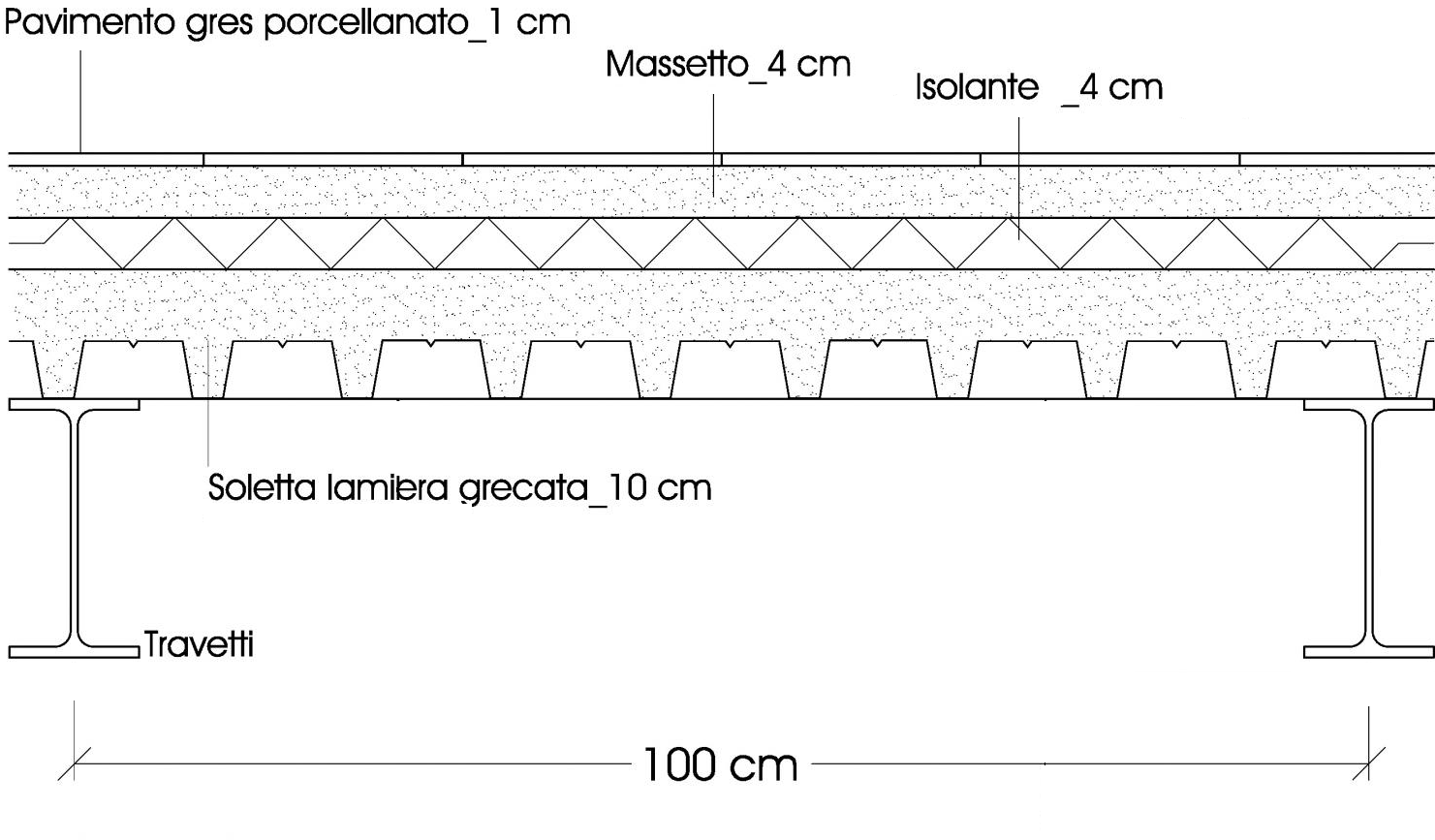  Fig. 4

        qa = 2.00 KN/m²  

Dal tabulario delle IPE si ricava  l’altezza della trave corrispondente al modulo di resistenza a flessione (W_xmin).

Il valore di W_xmin calcolato nella tabella excel  è pari a 319 cm³, che corrisponde ad un IPE 240 con W_xmin = 324

L'altezza corrispondente al un IPE 240 è di 24 cm.

E' quindi possibile ricalcolare i carichi considerando il peso proprio della trave per la verifica del predimensionaento.

Per la realizzazione della struttura reticolare in 3 D si utilizza la template GRID ONLY e si  impostano i moduli a seconda della grandezza che si vuole ottenere, in questo caso la copertura reticolare è costituita da una piasta di moduli 16x11.

                                                                                                                                                         FIG.1

La travatura reticolare si ottiene disegnando direttamente nel programma Sap con lo strumento DRAW FRAME. Una volta realizzato il primo cubo controventato lo si può copiare e incollare verso l’asse x e verso l’asse y per riempire l’intera griglia.

Si ottiene la copertura reticolare  raffigurata nell’immagine sottostante.

FIG.2

 Realizzata la struttura è necessario assegnare ad ogni nodo il vincolo di cerniera interna  definendo il  momento nullo.

Quindi si prosegue definendo la geometria e il materiale della struttura, un tubolare in acciaio.

E’ fondamentale assegnare dei vincoli che determinano il tipo di appoggio della struttura, quindi si ipotizzano dei pilastri agli angoli esterni, vengono quindi inserite quattro cerniere.

                                                                                                                                                        FIG.3

Infine è possibile introdurre  i carichi, si sceglie di posizionare dei carichi di 20 KN su ogni nodo.

A questo punto è si può apprezzare la deformata della struttura e i diagrammi delle sollecitazioni.

                                                                                                                                                           FIG.4

                                                                                                                                                          FIG.5

                                                                                                                                                          FIG.6

Inoltre Sap dà la possibilità di osservare i risultati attraverso delle tabelle exel , nell’immagine sottostante vi è  un esempio di una parte della tabella ELEMENT FORSES_ FRAME.

                                                                                                                                                           FIG.7

Nell’immagine successiva vengono messe in evidenza  le aste sottoposte al maggiore e al minore  sforzo assiale.

                                                                                                                        FIG.8

La trave reticolare è composta da un’insieme di aste assemblate in modo tale da comporre dei moduli triangolari, la funzione delle aste diagonali è quella di garantire una certa rigidezza della struttura. Nella parte superiore ed inferiore della trave sono riconoscibili due serie di aste allineate, i correnti superiori hanno un dimetro maggiore mentre quelli inferiori sono più sottili.

Introducendo delle forze esterne agenti sui nodi della trave reticolare potremo verificare, attraverso l’utilizzo del programma Sap 2000 che le aste sono sollecitate da sforzi normali.

FIG.1

E’ stata disegnata quindi una  trave reticolare con tre divisori e sono state applicate dei carichi esterni sui tre nodi pari a 10 KN.

FIG.2

Conseguentemente si possono osservare le reazioni vincolari che come si può facilmente verificare sono pari a 15KN su entrambi i vincoli.

FIG.3

Nella deformazione della trave le aste superiori saranno compresse e le inferiori tese, ciò è osservabile facendo riferimento all’immagine della deformata flessionale della trave, visibile in seguito.

FIG.4

Dal diagramma dello sforzo normale e dalle tabelle ottenute si ha un’indicazione grafica e numerica della sollecitazione massima e minima.

FIG.5

FIG.6

Di seguito sono state evidenziate le sollecitazioni normali massime e minime differenziate da colori sia sulla struttura che in tabella.

FIG.7

L’asta maggiormente sottoposta a sforzo normale è quella centrale, seguono le aste superiori, numero 4 e 5, quelle gialle nmero 1, 3, 6, 11 e in fine quelle centrali.

  FIG.8

prova