III Esercitazione _ Dimensionamento e deformabilità di una trave a sbalzo

In questa esercitazione si analizzerà la deformabilità di una trave a sbalzo in tre diversi materiali, in calcestruzzo armato, in legno e in acciaio. Si studia il telaio mostrato in figura sottostante, con interasse pari a 3 m e luce dello sbalzo pari a 3 m, in cui viene evidenziata la trave maggiormente sollecitata.

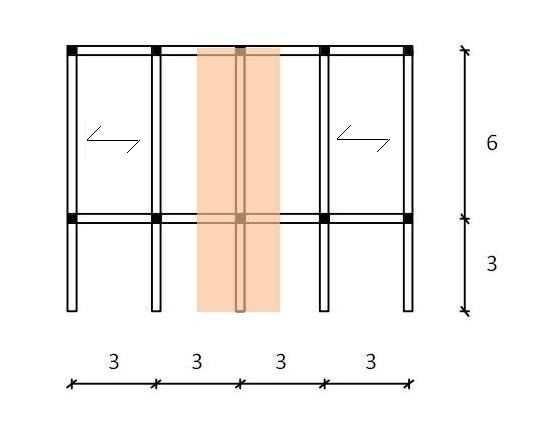                                    Fig. 1

Per calcolare la deformabilità di una trave a sbalzo, come è stato fatto nell’esercitazione precedente della trave appoggiata, prima di tutto è necessario calcolare i carichi agenti su di essa.

SOLAIO IN CLS

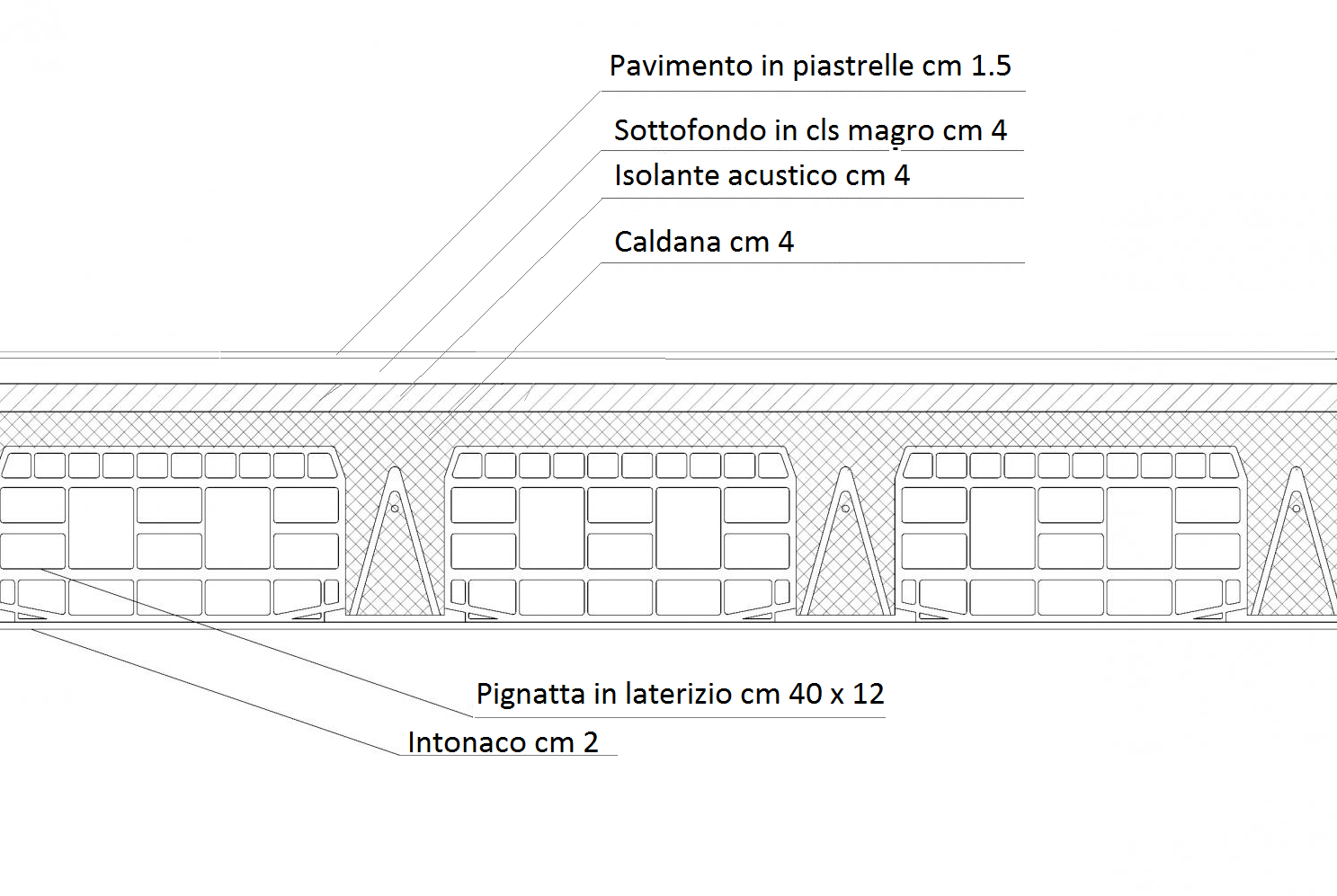                                    Fig. 2

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

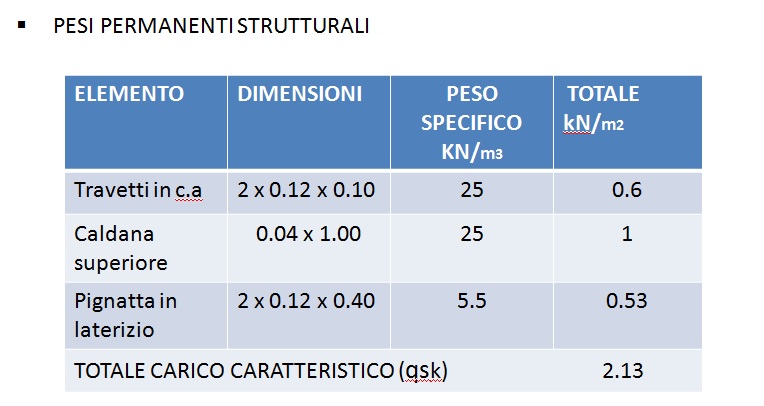
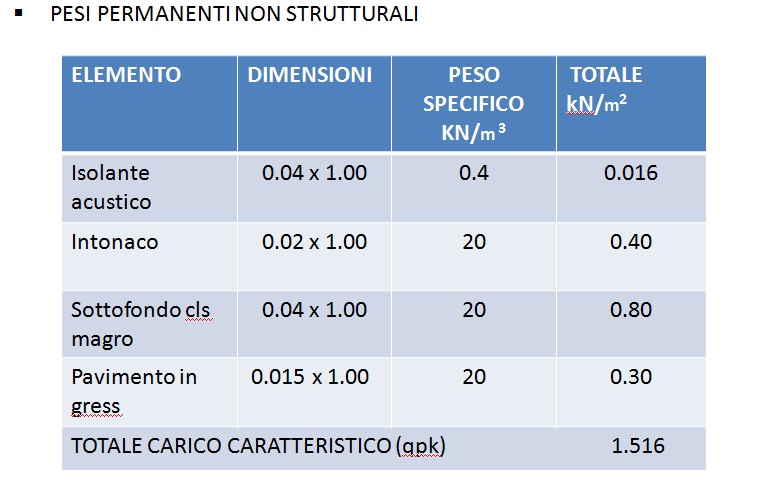
Carichi strutturali qs=    2.13    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. E' inoltre necessario inserire il valore pari 450 MPa per la resistenza caratteristica delle armature e scegliendo una classe C 40/50 per il cls si definisce anche la resistenza caratteristica a compressione pari a 50 Mpa.

Infine si sceglie la base della trave pari a 30 cm e si ottine l'altezza.

L'altezza della trave risulta essere pari a 28.73 cm questo valore viene arrotondato a 35 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.35 m x 1 m ) x 25KN/m³ = 2.625 KN/m

l/Vmax>250 è verificata poiché l/Vmax =341 e si ha uno spostamento Vmax pari a 0.88 cm.

SOLAIO IN LEGNO

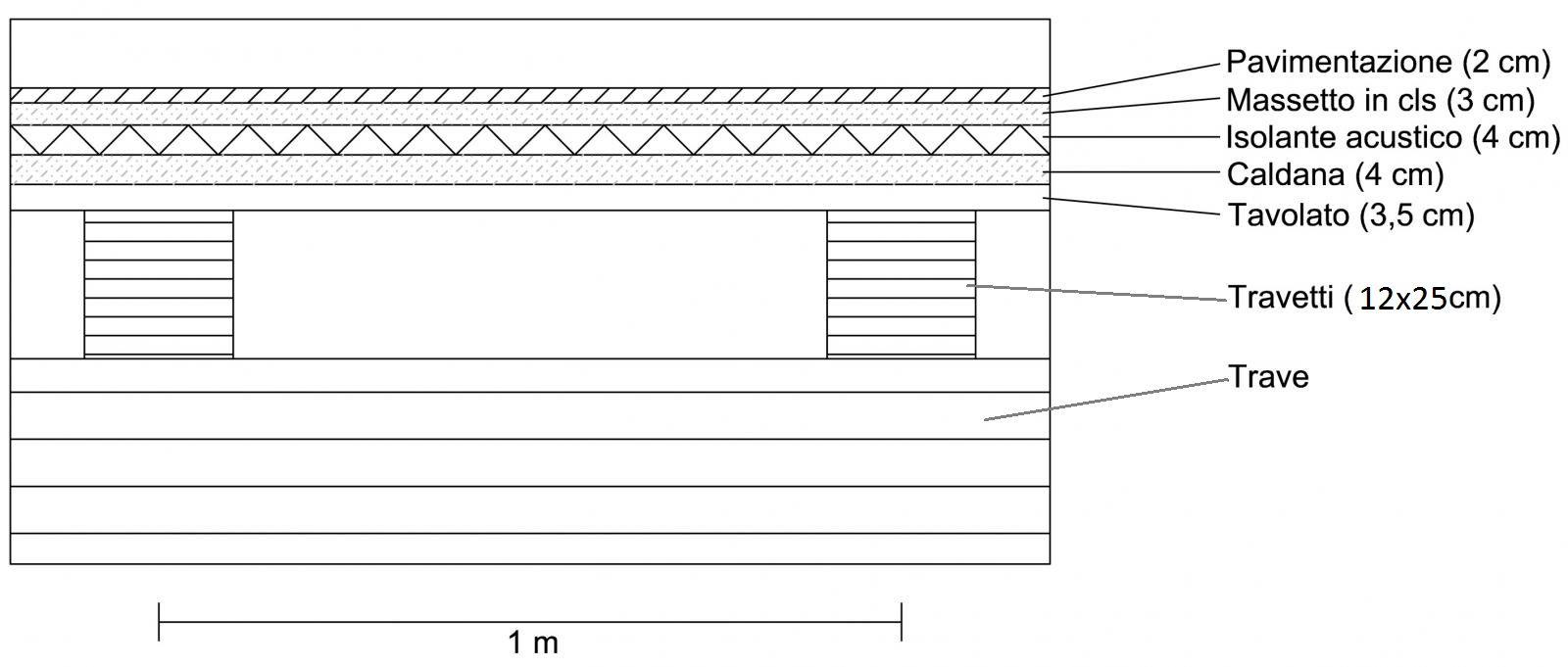Fig. 3

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

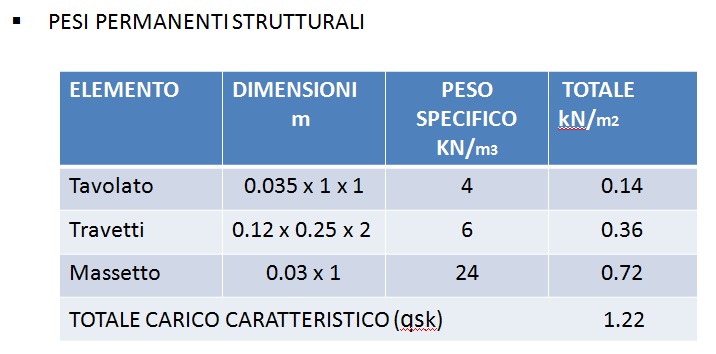
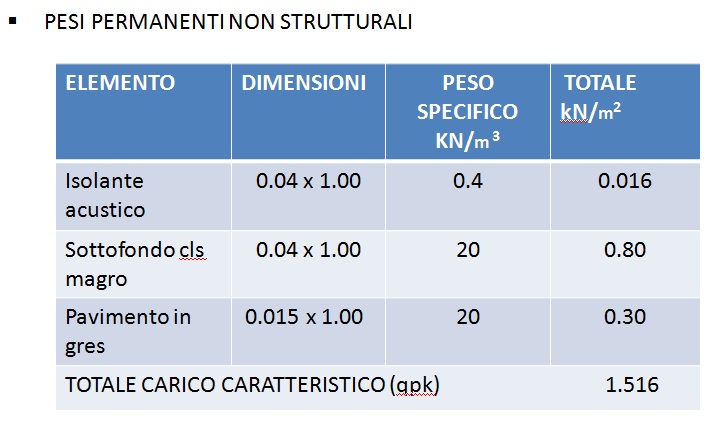
Carichi strutturali qs=    1.2    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. Si è scelto un legno lamellare GL 24h con resistenza a flessione fm,k = 24MPa e la base della trave pari a 30cm.

Considerando la base della trave pari a 30 cm si ottiene un'altezza pari a 36.4 cm che si arrotonda a 40 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.40 m x 1 m ) x 7 KN/m³ = 0.84 KN/m

l/Vmax>250 è verificata poiché l/Vmax =265 e si ha uno spostamento Vmax pari a 1.13 cm.

SOLAIO IN ACCIAIO

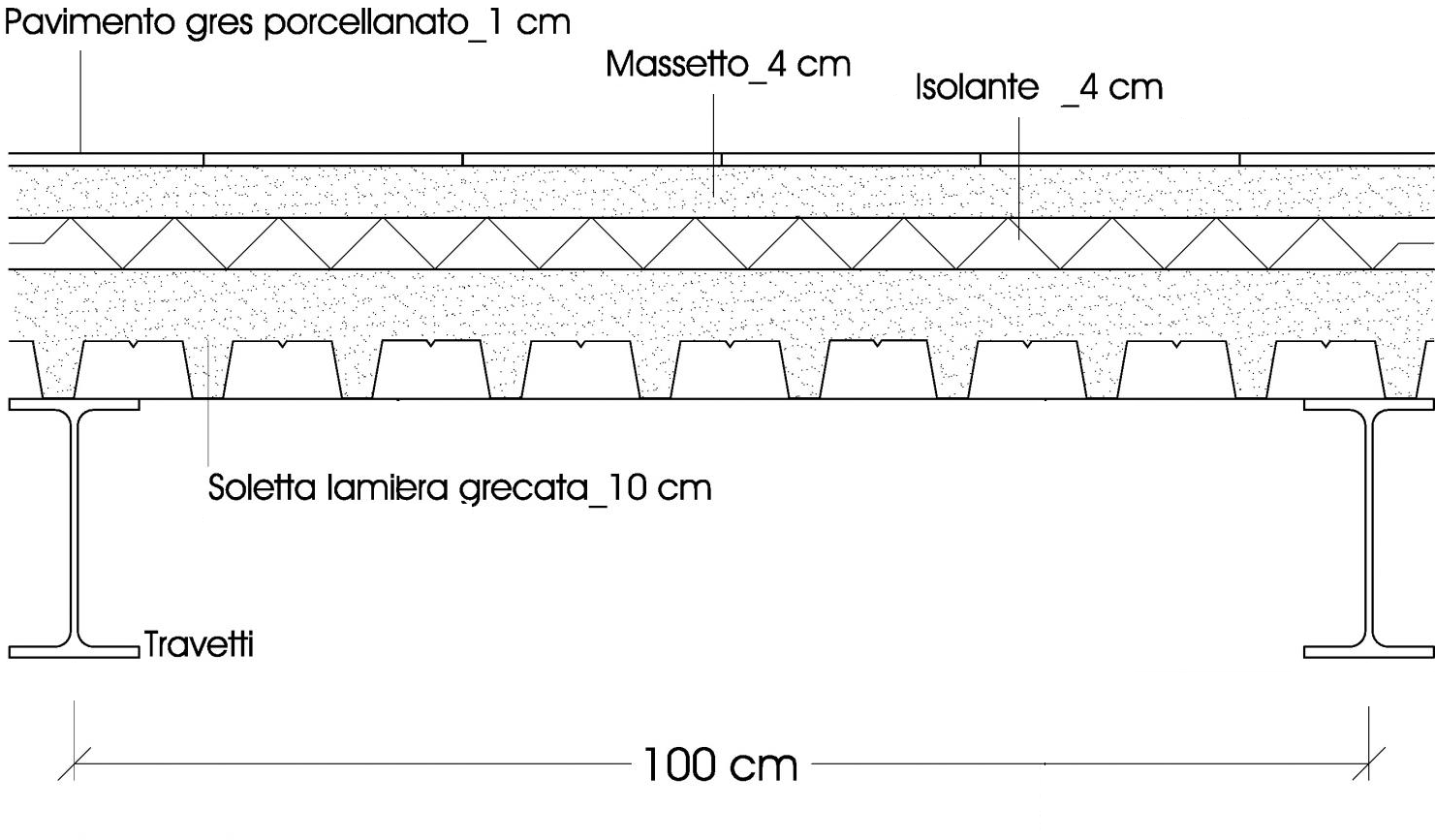
In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

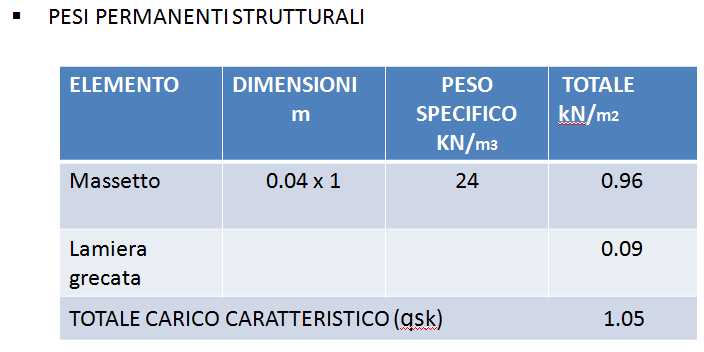
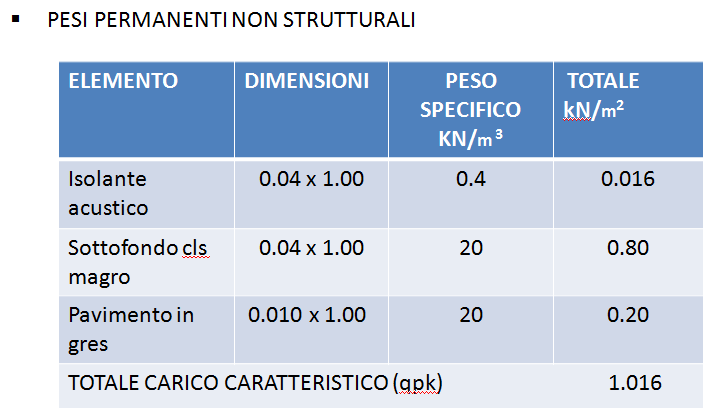
Carichi strutturali qs=    1    Kn/ m²

Carichi permanenti qp=  1   KN/m²

Carichi accidentali qa=    2   KN/m²

Per dimensionare una trave in acciaio, una volta che si conosce la Wx è possibile ricavare la sezione dal profilario.

Quindi si sceglie una IPE 220 con una Wx=252 cm³ e Ix= 9110 cm⁴ .

Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

P= (0.0033 m² x 1m)/m x 78,50 KN/m³= 0.259 KN/m

l/Vmax>250 è verificata poiché l/Vmax =374 e si ha uno spostamento Vmax pari a 0.8 cm.

In tutte le tecnologie considerate nel caso in cui la verifica non fosse stata soddisfatta si sarebbe dovuta modificare la sezione oppure la luce.