blog di Laura Rosati

Gli archi rientrano nella categoria di strutture che lavorano per forma e non per massa. Sono strutture spingenti, che ottimizzano al meglio il materiale lavorando a sforzo normale, molto efficaci nel superamento di grandi luci

ARCO CIRCOLARE ISOSTATICO A TUTTO SESTO:

Dopo aver disegnato l'arco su autocad e averlo importato in dxf su sap si procede all'analisi della struttura.

si impostano le tre cerniere all'imposta e in chiave, rilasciando in chiave il momento in corrispondenza della cerniera.

seleziono l'arco e assegno una sezione rettangolare 0,3 m x 0,4 m

SI assegna poi il carico distribuito lungo la linea d'asse dell'arco, e non sulla sua proiezione a terra (comando: assign-frame loads-distribuited)

Come si nota il valore dello sforzo assiale fa capire come il carico si sia distribuito equamente sui due tratti dell'arco e che è massimo all'imposta ( Q*luce) e la metà in chiave (Q*luce/2). Inoltre il grafico del momento dimostra il suo annullamento in corrispondenza delle tre cerniere in chiave e alle imposte.

 

ARCO PARABOLICO:

Con lo stesso procedimento dell'arco precedente si procede all'analisi dell'arco parabolico. Ci si aspetta che il taglio e il momento flettente siano nulli e che il carico uniformemente ripartito sull'orizzontale si trasformi completamente in sforzo normale (è infatti un arco funicolare e non catenario).

impongo le tre cerniere e il rilascio del momento in chiave in corrispondenza della cerniera interna, e applico sempre un carico distribuito.

Il valore dello sforzo normale all'imposta corrisponde al valore della spinta dell'arco parabolico.

 

 

Per poter resistere a forze sismiche, cioè orizzontali, è necessario che le strutture siano in qualche modo controventate, e in generale ogni telaio dell'edificio rappresenta un controvento. In questo caso i telai sono di tipo Shear-type, modello teorico ideale di telaio, dove i nodi sono tutti incastri e la trave è infinitamente rigida (molto resistente a flessione) con momento di inerzia maggiore di quello dei pilastri: essa prende la maggior parte del momento e del taglio. La deformata vedrà quindi la trave soggetta solo a traslazione orizzontale rigida (con solo spostamento) e non a deformazione assiale, e avendo rotazione nulla all'incastro essa "trascinerà" i pilastri che quindi si deformeranno in quanto soggetti a flessione.

Alla forza orizzontale che agisce sull'impalcato (che diventa corpo rigido piano), il telaio reagirà con altrettante forze orizzontali, cioè i tagli che nascono in corrispondenza di ogni pilastro. Il legame che sussiste tra il taglio in quel punto e lo spostamento della trave è la rigidezza k del controvento. In corrispondenza di ogni controvento della struttura è perciò rappresentata una molla, che indica la rigidezza di ogni controvento della struttura.

Decisa l'altezza dei pilastri pari a 4 m e la loro sezione pari a 40 cm x 40cm, e il materiale, ( c.a.), con il supporto di un foglio excel si determina il centro delle rigidezze del telaio e la ripartizione delle forze sismiche.

STEP 1: si calcolano le rigidezze traslanti dei controventi dell'edificio analizzando telaio per telaio. Si inseriscono quindi i valori di E, H, I, e ottengo la rigidezza di ogni telaio.

E, modulo di elasticità del c.a. con classe di resistenza C 25-30 è pari a 31500 MPa (N/mm²)

H = 4 m

I = bh³/12= 213333 cm⁴

STEP 2: la tabella mostra tutte le rigidezze dei vari controventi, e le loro distanze dal punto di origine , cioè in corrispondenza del pilastro 8.

STEP 3:  calcolo delle coordinate del centro delle masse (baricentro, dove "confluiscono" le forze esterne applicate alla struttura). Si suddivide l'area totale dell'impalcato in aree più piccole, di cui si calcolano i singoli centri di massa, ottenendo poi le coordinate del centro di massa dell'intera struttura.

STEP 4:  calcolo delle coordinate del centro delle rigidezze

STEP 5:  dati i carichi di un solaio in c.a. (presi dalla scorsa esercitazione) e moltiplicati per l'area dell'impalcato si ottengono G e Q totali sulla struttura. Essi si moltiplicano per il coeff. di contemporaneità ottenendo i pesi sismici W, da moltiplicare a loro volta per il coeff. di intensità sismica, ottenendo la forza sismica totale agente.

STEP 6-7:  si ottiene quindi la ripartizione delle forze sismiche Fx e Fy, il momento torcente Mx e My ricavati moltiplicando la forza sismica per la differenza tra le coordinate (le x per My e le y per Mx) del centro delle rigidezze e delle masse (quindi M_x= F(Y_C-Y_G) e M_y= F(X_C-X_G) ).

Lo spostamento traslante lungo la direzione x sul piano dove giace l'impalcato è pari a δ   ( da F= K x δ)

La rotazione dell’impalcato = Mx/ K_tot

Le forze su ciascun controvento si ricavano moltiplicando: rigidezza controvento * distanza dall’origine del controvento * rotazione impalcato.

 

Si realizza la struttura su SAP per verificare la deformata e avere i valori delle sollecitazioni

Attraverso lo strumento Grid Only realizzo una griglia di base su cui costruire i telai della struttura, e assegno poi vincolo di incastro alla base dei pilastri disegnati.

Si assegna poi la sezione dei pilastri e delle travi (per renderle idealmente infinitamente rigide vado ed aumentare il modulo E e l'altezza della sezione è anch'essa molto alta).

Si disegna poi il centro delle masse sul piano dell'impalcato dato dalle coordinate calcolate prima in excel.

Dopo aver impostato la forza sismica agente sul centro delle rigidezze si ottiene la deformata classica del modello di telaio shear-type, dove ogni punto del piano orizzontale del solaio trasla orizzontalmente. Si nota anche una leggera rotazione dell'impalcato, dovuta al fatto che il centro delle masse non coincide precisamente con il baricentro della strutttura

L’orditura del solaio considerato (edificio ad uso residenziale) prevede travi appoggiate e uno sbalzo di 3 metri; verrà dimensionata la mensola utilizzando un foglio di calcolo excel, effettuando la verifica a deformabilità della trave. Verranno considerate tre diverse tipologie di solaio, con tecnologia in legno, c.a. e acciaio. Molto importante, così come per la trave su appoggi, sarà la luce l, in questo caso lunghezza dello sbalzo pari a 3 m, e l’interasse pari a 5 m.

La composizione dei solai è ripresa dall’esercitazione 2 sulla trave appoggiata.

 

SOLAIO IN LEGNO

1: travetto                                    12x22 cm

2: impalcato                                 5 cm spessore

3: cls caldana                               7 cm spessore

4: isolante                                     5 cm spessore

5: massetto di allettamento         2 cm spessore

6: parquet, listelli 20x100 cm;      2 cm spessore

Si calcolano i carichi strutturali qs, accidentali qa, permanenti qp

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          impalcato           0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti                 1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq                  

 qs = 0,36 kN/mq

carichi permanenti qp :

-          pavimento in parquet         0,02 m * 6,9 kN/mc =  0,14 kN/mq   

-          massetto in cls leggero      0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                               0,05 m * 0,4 kN/mc = 0,02 kN/mq

-          cls caldana                          0,07 m * 24 kN/mc = 1,68 kN/mq

-          incidenza impianti              1 kN/mq     (da normativa)

-          incidenza tramezzi              0,5 kN/mq  (da normativa)                             

qp = 3,62 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = qa + qs + qp = 5,98 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5

totale carichi = 8,17 kN/mq

Andando a moltiplicare questo valore per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 40,87 kN/m

Si imposta poi l= lunghezza dello sbalzo, ottenendo un valore del Momento massimo (ql²/2) pari a:

M = 183,92 KNm

Viene poi calcolata la resistenza di progetto, definita dal prodotto tra resistenza caratteristica del legno e il coefficiente di degrado nel tempo Kmod,  diviso per il coefficiente di sicurezza:  

σ_amm= 13,24 N/mm²

con la formula di Navier so che  σ_amm = Mmax/ Wmax

inoltre W_max = bh²/ 6 la cui formula inversa permette di calcolare la sezione impostando un valore alla base della trave b.

Viene poi inserito il valore dell’altezza h_d ingegnerizzata = 50 cm, e il valore del modulo E di elasticità che sarà 11600 N/mm²  per un legno lamellare classe GL24.

Si avrà poi il valore del modulo di inerzia I_x = bh³/12 per sezione rettangolare.

Ciò che si ottiene è infine il valore massimo dell’ abbassamento, che è uno spostamento lineare (risolto nelle strutture isostatiche con il metodo degli spostamenti).

v_max= ql⁴/8EI_x = 0,86 cm

per avere un valore di abbassamento accettabile, rispetto alla struttura in esame, esso non deve superare 1/250 della luce, quindi se  

l/ v_max ≥ 250.

Ottenendo quindi  l/ vmax = 350,40 il valore dello spostamento è accettabile.

Inserendo ora anche il peso proprio della trave calcolata si verifica infine la mensola

carichi strutturali  qs :

-          impalcato           0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti              1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq  

-          trave                 0,5 m * 0,4 m * 3,80 kN/mc = 0,76 kN/ mq 

           valore al mq assimilabile a quello al metro lineare

dove 380 kN/ m³  è il peso specifico del legno lamellare classe GL24

 qs = 1,12 kN/mq

Inserendo il nuovo valore del carico strutturale si ottiene comunque anche considerando il peso proprio della mensola un valore ammissibile di spostamento massimo.

 

 

 

SOLAIO IN ACCIAIO

1: trave                                       

2: lamiera grecata                             6 cm spessore

3: massetto cls                                  5 cm spessore

4: isolante                                         4 cm spessore

5: massetto                                       6 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          massetto cls         0,11 m * 24 kN/mc = 2,64 kN/mq

-          lamiera grecata   0,24 kN/mq                                                             

qs = 2,88 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato 0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero 0,06 m * 14 kN/mc = 0,84 kN/mq

-          isolante 0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          incidenza impianti 1 kN/mq

-          incidenza tramezzi 0,5 kN/mq                                                                     

qp = 2,66 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

Andando a moltiplicare il valore del carico totale per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 42,7 kN/m

vengono poi individuati i valori di Momento massimo, la resistenza caratteristica del materiale fd  in base alla tensione di snervamento dell’acciaio fyk, e Wx (usando la formula di Navier σamm= Mmax/ Wmax) cioè il modulo di resistenza minimo a flessione. In base a quest’ultimo valore si è scelta una trave IPE 400; l’altezza della trave sarà quindi di 40 cm, il peso = 66,3 kg/m, Ix = 23130, da cui si ottiene un carico totale (compresa la trave) di 49,33 kN/m.

L’abbassamento risulta di 1,02 cm e ammissibile rispetto alla struttura.

SOLAIO IN LATERO-CEMENTO

1: pignatte                                     40 x 16 cm                                      

2: travetti                                       10 x 16 cm  

3: caldana cls                                 4 cm spessore

4: isolante                                       4 cm spessore

5: massetto alleggerimento           4 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          caldana         0,04 m * 24 kN/mc = 0,96 kN/mq

-          travetti          2* 0,10 m * 0,16* 24 kN/mc = 0,77 kN/m

 qs = 1,73 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato         0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero           0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                                   0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          pignatte                                   2 * 0,4 m * 0,16 m * 8 kN/mc = 1,02 kN/mq

-          incidenza impianti                    1 kN/mq

-          incidenza tramezzi                  0,5 kN/mq

qp = 3,12 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = 6,85 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5                                                                       

Andando a moltiplicare il valore del carico finale per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 46,52 kN/m

Come nei casi precedenti si ottiene il valore del momento massimo che agisce sulla sezione.

Si inseriscono nel calcolo le resistenze dei materiali: acciaio di armatura e calcestruzzo, rispettivamente fy e fck. Si imposta una base di 30 cm e si ricava quindi il predimensionamento della sezione di altezza 45 cm (considerando lo spessore del copriferro di 5 cm).

Si ottengono di conseguenza gli altri valori necessari per la verifica all’abbassamento, quali il modulo E, il momento di inerzia della sezione rettangolare e il peso proprio della trave.

Anche in questo caso, come nei precedenti si ottiene un abbassamento ammissibile dalla struttura pensata.

Conclusioni: effettuando altre prove di calcolo sul foglio di calcolo l’aspetto più importante per un aggetto è la luce, nel caso del c.a. essa al massimo può arrivare ad allungarsi di soli 40 cm per poter ancora considerare lo spostamento ammissibile in tali condizioni di carico; 20 cm per il legno e soli 10 cm per l’acciaio!

 

 

 

Dopo aver definito l’orditura del solaio (edificio ad uso residenziale) e aver scelto le componenti delle tre diverse tipologie tecnologiche da analizzare, legno, acciaio e cemento armato, attraverso il supporto del foglio di calcolo excel, si è potuto effettuare un dimensionamento della trave più sollecitata della struttura nei tre diversi casi.

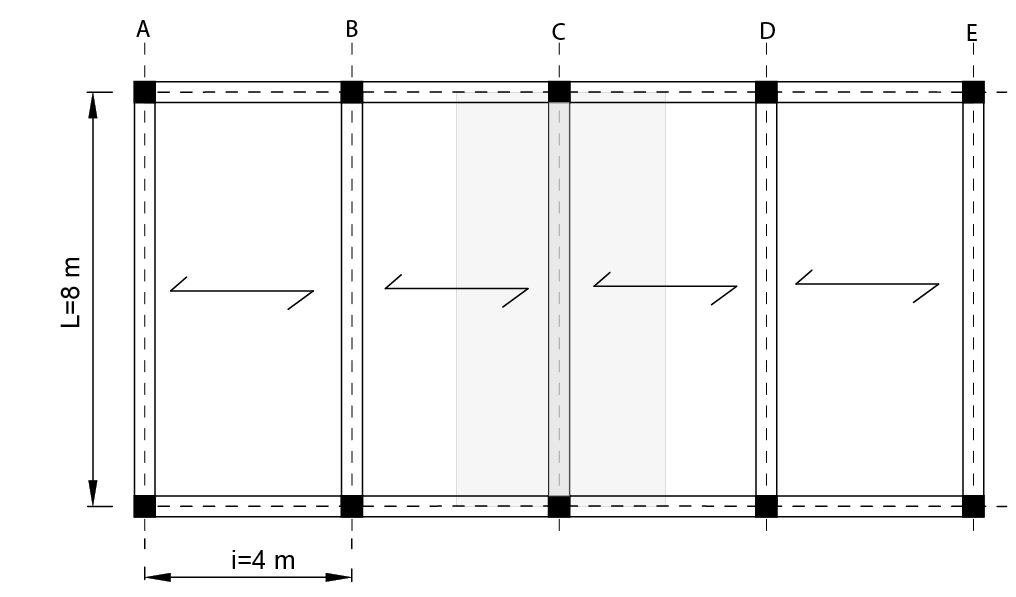
Si è considerata la trave C come una delle più sollecitate, in base alla partizione del carico. L’ area di influenza del carico sulla trave considerata è A = 8 x 4= 32 mq

Legno

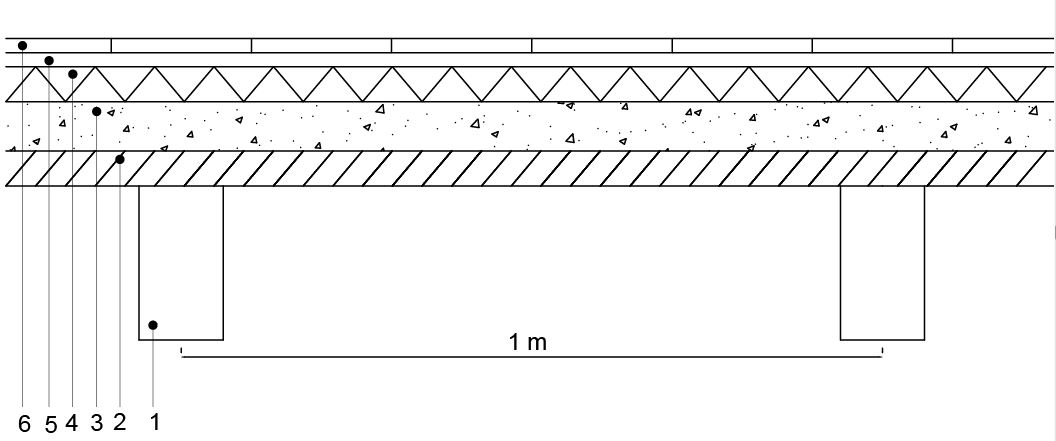
1: travetto                                    12x22 cm

2: impalcato                                 5 cm spessore

3: cls caldana                               7 cm spessore

4: isolante                                     5 cm spessore

5: massetto di allettamento         2 cm spessore

6: parquet, listelli 20x100 cm;      2 cm spessore

 

Si calcolano quindi i carichi strutturali qs, accidentali qa, permanenti qp

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          impalcato           0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti                 1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq                  

 qs = 0,36 kN/mq

 

carichi permanenti qp :

-          pavimento in parquet         0,02 m * 6,9 kN/mc =  0,14 kN/mq   

-          massetto in cls leggero      0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                               0,05 m * 0,4 kN/mc = 0,02 kN/mq

-          cls caldana                          0,07 m * 24 kN/mc = 1,68 kN/mq

-          incidenza impianti              1 kN/mq     (da normativa)

-          incidenza tramezzi              0,5 kN/mq  (da normativa)                             

qp = 3,62 kN/mq

 

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

 

q = 5,98 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5

totale carichi = 8,17 kN/mq

Andando a moltiplicare questo valore per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 32,7 kN/m

Successivamente al calcolo del carico distribuito si calcola il momento massimo Mmax. 

M = (q*L²)/8

Mmax = (32,7*8²)/8 = 261,6 Knm

Viene poi calcolata la resistenza di progetto, definita dal prodotto tra resistenza caratteristica del legno e il coefficiente di degrado nel tempo Kmod,  diviso per il coefficiente di sicurezza:  

σ_am= 13,24 N/mm²

Impostando poi la base della trave si ricava l’altezza (con la formula di Navier)

Dopo aver calcolato la sezione della trave (ingegnerizzata) andrà aggiunto il suo peso proprio, moltiplicando la sezione per la lunghezza della trave e per il peso specifico del materiale. Una volta calcolato in nuovo momento si verifica la resistenza della trave. Si ripete perciò il procedimento aggiungendo il peso proprio della trave ai carichi strutturali.

Si è scelto il legno lamellare classe GL 24 h con peso specifico di 3,80 kN/ mc

carichi strutturali qs :

-          impalcato          0,05 m * 4 kN/mc = 0,2 kN/mq

-          travetti              1 * 0,22 m* 0,12 m * 6 kN/mc = 0,16 kN/mq                       

-          trave                    0,3 m * 0,65 m * 3,80 kN/mc =   0,74 kN/mq                    

qs = 1,1 kN/mq

Si ottiene in questo modo una trave più alta di 4 cm. Andrà quindi ingegnerizzata adeguatamente rispetto al primo caso, anche se comunque lo scarto non risulta eccessivo.

Acciaio                      

 

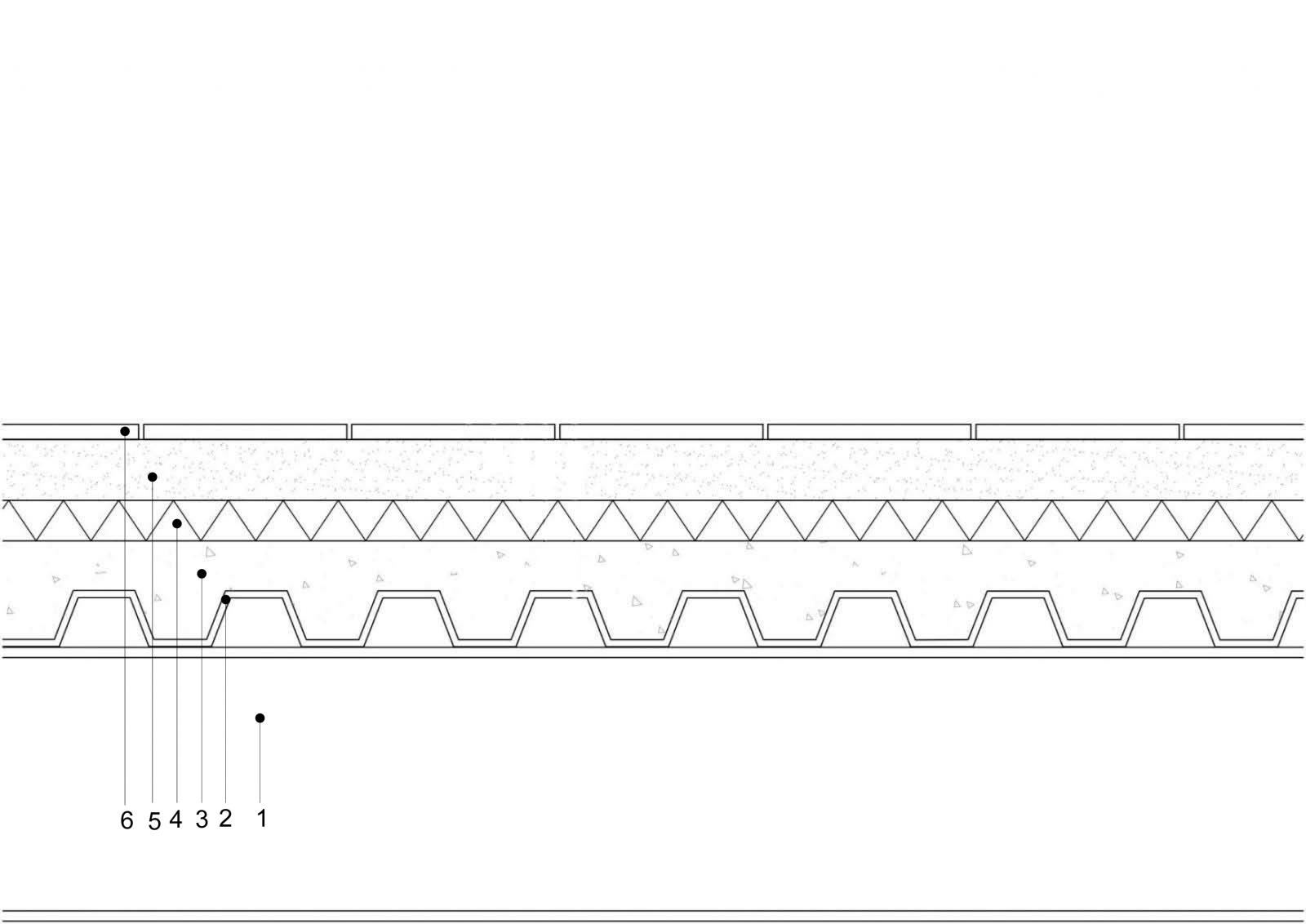
1: trave                                       

2: lamiera grecata                            6 cm spessore

3: massetto cls                                  5 cm spessore

4: isolante                                         4 cm spessore

5: massetto                                       6 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          massetto cls         0,11 m * 24 kN/mc = 2,64 kN/mq

-          lamiera grecata   0,24 kN/mq                                                             

qs = 2,88 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato 0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero 0,06 m * 14 kN/mc = 0,84 kN/mq

-          isolante 0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          incidenza impianti 1 kN/mq

-          incidenza tramezzi 0,5 kN/mq                                                                     

qp = 2,66 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = 7,54 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5                                                                       

Andando a moltiplicare questo valore per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 40,8 kN/m

Si inserisce poi la resistenza caratteristica dell’acciaio in normativa ottenendo così σ_{am e Wx}

L’IPE corrispondente al modulo di resistenza a flessione Wx in questo caso è l’IPE 450, con altezza quindi di 45 cm.

 

Si inserisce ora il peso proprio della trave nei carichi strutturali per la verifica:

carichi strutturali qs :

-          massetto cls         0,11 m * 24 kN/mc = 2,64 kN/mq

-          lamiera grecata   0,24 kN/mq                             

-          trave IPE 450        0,77 kN/m2                                                          

         qs = 3,65 kN/mq         

Il risultato porta sempre a scegliere un profilato in acciaio IPE 450, ciò significa che in questo caso il peso proprio della trave non influisce in modo rilevante sul dimensionamento.

 

Cemento

      

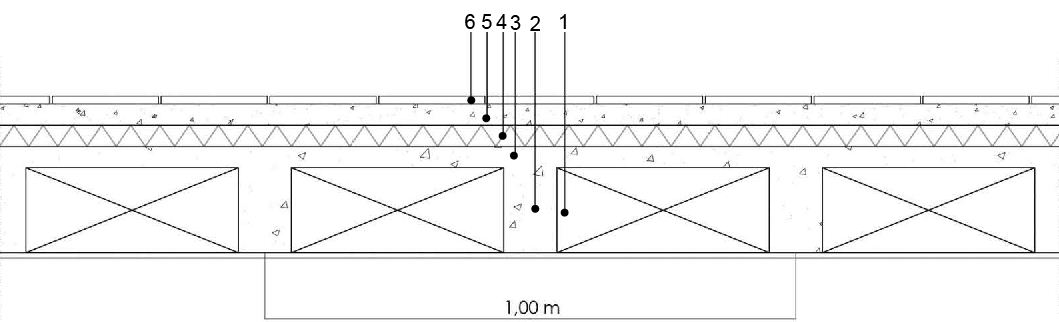
1: pignatte                                     40 x 16 cm                                      

2: travetti                                       10 x 16 cm  

3: caldana cls                                 4 cm spessore

4: isolante                                       4 cm spessore

5: massetto alleggerimento           4 cm spessore

6: pavimento gres porcellanato     1,5 cm spessore

 

carichi strutturali  (si esclude per ora il peso proprio della trave) qs :

-          caldana         0,04 m * 24 kN/mc = 0,96 kN/mq

-          travetti          2* 0,10 m * 0,16* 24 kN/mc = 0,77 kN/m

 qs = 1,73 kN/mq         

carichi permanenti qp :

-          pavimento in gres porcellanato         0,015 m * 20 kN/mq = 0,3 kN/mq

-          massetto in cls leggero           0,02 m * 14 kN/mc = 0,28 kN/mq

-          isolante                                   0,04 m * 0,4 kN/mc = 0,016 kN/mq

-          pignatte                                   2 * 0,4 m * 0,16 m * 8 kN/mc = 1,02 kN/mq

-          incidenza impianti                    1 kN/mq

-          incidenza tramezzi                  0,5 kN/mq

qp = 3,12 kN/mq

carichi accidentali qa:

-          ambiente residenziale        2,00 kN/mq                                                        

qa = 2,00 kN/mq

q = 6,85 kN/mq

-          coefficienti di sicurezza: ogni carico va moltiplicato per un coefficiente di sicurezza

γs = 1,3 

γp = 1,3 

γA= 1,5                                                                       

Andando a moltiplicare questo valore per l’interasse si ottiene il carico che agisce sulla trave considerata.

q = 37,22 kN/m

Come nei casi precedenti si ottiene il valore del momento massimo che agisce sulla sezione.

Si inseriscono nel calcolo le resistenze dei materiali: acciaio di armatura e calcestruzzo, rispettivamente fy e Rck. Si imposta una base di 30 cm e si ricava quindi il predimensionamento della sezione di altezza 52,21 cm (considerando lo spessore del copriferro di 5 cm).

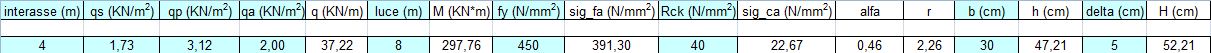
Si inserisce ora il peso proprio della trave nei carichi strutturali per la verifica:

carichi strutturali qs :

-          caldana         0,04 m * 24 kN/mc = 0,96 kN/mq

-          travetti          2 * 0,10 m * 0,16 * 24 kN/mc = 0,77 kN/m

-          trave              0,3 * 0,54 * 25 kN/mc =  4,05 kN/m             

qs = 5,78 kN/mq         

Considerando anche il peso proprio della trave si ottiene una sezione ingegnerizzata di 65 cm. A differenza del legno e dell’acciaio, in cui il peso proprio della struttura non incideva molto sul dimensionamento, per il cemento armato invece si ha uno scarto di più di dieci cm se si considera anche la trave nel calcolo del carico strutturale, e ciò è dovuto all’elevato peso specifico del calcestruzzo.

2D

Utilizzando Sap2000 è stato possibile verificare una struttura di tipo reticolare precedentemente calcolata individuando i valori degli sforzi assiali e la tipologia di asta (puntone o tirante):

Si è quindi utilizzato un modello predefinito di trave reticolare su due appoggi in 2d come quello analizzato precedentemente assegnando  le dimensioni in rapporto 1:2 (così da ottenere l’angolo tra il corrente e i diagonali α=45°).

File – New Model – 2D Trusses

Dopo aver impostato le corrette unità di misura sono state quindi assegnate le dimensioni L=3 m e H=2L=6m, ottenendo quindi il modello seguente:

Si vanno poi a considerare i nodi come cerniere interne, in modo tale che il momento all’inizio e fine di ogni asta sia nullo (dopo aver selezionato tutte le aste, attraverso il comando Frame – Releases), operando quindi un “rilascio” del momento.

Successivamente si definiscono i carichi concentrati applicati in corrispondenza dei nodi superiori della trave (tre forze puntuali verso il basso).

Si selezionano i nodi superiori e con il comando  Assign – Joint Loads – Forces si imposta un carico F=100 KN lungo l’asse z, ottenendo quindi una struttura simmetrica geometricamente e anche dal punto di vista dei carichi su essa applicati. Non viene considerato il peso proprio della struttura

A questo punto si sceglie la sezione e il materiale delle aste, in questo caso tubolari in acciaio.

Si avvia quindi l’analisi delle sollecitazioni, ottenendo la configurazione deformata e il diagramma dello sforzo assiale con i valori riportati relativi ai vari tratti della struttura (che confermano le soluzioni iniziali dell’esercizio calcolato a mano).

Una volta assegnata una numerazione per le aste della trave si possono facilmente individuare nella tabella  Excel di sintesi dei risultati ottenuti dall’analisi

Come evidente anche dalla configurazione deformata della trave, nei valori in tabella si può osservare che:

- l’asta più sollecitata è la centrale inferiore

- i valori di taglio sono nulli e l’unica sollecitazione è di sforzo normale N (che nella tabella corrisponde alla colonna F1)

-dove N è positivo si hanno tiranti, dove è negativo puntoni

Inoltre si nota anche la simmetria della struttura già definita precedentemente a livello geometrico e qui confermata anche a livello di carico e sollecitazioni;

Il modello di trave utilizzato non corrisponde in realtà ad una realistica trave reticolare, che infatti prevede una luce molto più grande rispetto a questa data dal modello predefinito utilizzato, pertanto nella seguente  modellazione 3D la struttura sarà sempre reticolare ma dimensionalmente realistica.

3D

Per la modellazione tridimensionale si è scelta una struttura reticolare di un solaio 15x30 m.

 

Seguendo le stesse procedure del 2D (inserimento dei vincoli, rilascio momento alle cerniere interne, determinazione del materiale e della sezione, distribuzione dei carichi) si effettua l’analisi delle sollecitazioni.

La distribuzione dei carichi prevede quindi una porzione della struttura in aggetto, e si nota inoltre dalla deformata che i vari tratti se presi singolarmente si comportano come modello di mensola o come trave appoggiata.

prova!!!!!!