blog di Virginia Pucello

La travatura reticolare è una struttura composta da un insieme di aste vincolate ai nodi, in modo da costituire un elemento resistente in grado di superare luci molto grandi. È formata da due elementi continui chiamati correnti, uno superiore e uno inferiore, collegati da altri elementi disposti alcuni in verticale e altri inclinati. Gli elementi verticali vengono denominati montanti, quelli inclinati diagonali. 
Questa seconda esercitazione prevede dunque la modellazione in tre dimensioni di una travatura reticolare, sui cui nodi superiori vengono applicati dei carichi concentrati, al fine di analizzare la deformazione e fare la verifica a sforzo normale. Essendo le travi reticolari sollecitate solo a sforzo normale, non troveremo sollecitazioni di taglio e momento. Il disegno tridimensionale della travatura può avvenire su cad o rhino, importandolo poi in sap, oppure direttamente su sap, preimpostando una griglia. Scelgo quest’ultimo metodo, quindi mi costruisco la griglia andando su File->New Model->Grid Only

Impostata la griglia, ricalco con Draw Frame un cubetto di dimensioni 2x2x2, controventato su ogni faccia con una diagonale, che poi ripeto per tutta la griglia. Questo è il risultato.

Adesso devo assegnare i vincoli ai quattro punti in basso all’estremità della griglia, e scelgo delle cerniere, andando su Assign->Joint->Restraints

Trasformo poi le aste della travatura in aste incernerate al loro interno, selezionando tutto, andando su

Assign->Frame->Releases/Partial Fixity e spuntando Moment 22 (minor) e Moment 33 (major).

Il passo successivo è quello di assegnare una sezione alla travatura reticolare, ad esempio una sezione tubolare, che rinomino “pipe”: Assign->Frame->Frame Section

Ora stabilisco i carichi concentrati che andrò ad applicare sui nodi superiori della travatura: su Define->Load patterns aggiungo un modello di carico che chiamo “F” e, dopo aver selezionato la fascia superiore della travatura: Assign->Joint Loads->Forces. In questo modo assegno il valore di carico che ho stabilito, ovvero di 80 KN verso il basso lungo l’asse verticale z.

Posso a questo punto avviare l’analisi (Run Analysis), ottenendo la deformata derivante dal carico da me stabilito.

Visualizziamo il grafico dello sforzo normale andando su Frames/Cables/Tendons e spuntando Axial Forces, e mettiamolo a confronto con i diagrammi dello sforzo di taglio e del momento, che essendo nulli, non di segnano alcun grafico.

Per visualizzare i risultati dello sforzo normale di trazione e di compressione a cui le aste sono soggette, si va su Display->Show Tables e spunto la casella Analysis Results, specificando che siano i risultati derivanti dal carico F che ho applicato inizialmente. Mi si apre così la finestra dei risultati, dove imposto la voce Element Forces Frames.

Ottenendo il valore dello sforzo normale per ogni singola asta, posso esportare il foglio dei dati su un documento di calcolo excel e procedere con il dimensionamento delle aste. 
Avendo inizialmente impostato una lunghezza delle aste pari a 2*2*2, sotto la colonna “station” troverò due dimensioni: 2m per le aste dritte e 2,82843m per le diagonali.

Come passo successivo mi riordino la colonna degli sforzi normali di trazione (+) e compressione (-)  dal più piccolo al più grande, in modo tale da copiare i valori positivi nel foglio di dimensionamento a trazione e quelli negativi nel foglio di dimensionamento a compressione.

ACCIAIO ASTA RETICOLARE-TRAZIONE

Scelta la tipologia di acciaio, in questo caso S275, con una resistenza caratteristica di 275 MPA, trovo la resistenza di progetto, dividendo la resistenza caratteristica per il coefficiente di sicurezza 1,05 (fyd=fyk/1,05). Dopodichè facendo il rapporto tra lo sforzo normale e la resistenza di progetto, posso conoscere l’area minima che l’asta deve avere per potere resistere alla sollecitazione (Amin=N/fyd). Andando sulla tabella dei profilati metallici cerco un sezione circolare >/= all’area minima calcolata.

Per esempio se prendo in considerazione la prima riga, avendo un’area minima di 24,06 cm2 trovo sul profilario un’area superiore pari a 39,50 relativa al profilo 219*5,9 (mm).

Chiaramente avendo in tutto 366 aste, 171 per quelle tese e 194 per quelle compresse, non attribuirò a ciascuna  un profilo diverso, bensì quattro-cinque profili, a ognuno dei quali corrisponderà un intervallo di valori più o meno ampio. Alla fine allegherò le  intere pagine calcolate per la trazione e per la compressione. Qui proseguo nel mostrare giusto qualche esempio utile ai fini della spiegazione.

ACCIAIO ASTA RETICOLARE-COMPRESSIONE

Mantenuto l’acciaio S275 e calcolata prima la resistenza di progetto e poi l’area minima, seguendo lo stesso procedimento della trazione, per trovare l’area di progetto devo prendere in considerazioni più elementi, poichè un’asta soggetta compressione è esposta non solo alla crisi di rottura, ma anche a quella dello sbandamento, ovvero quando presenta una configurazione non rettilinea. Quest’ultimo fenomeno si verifica quando il carico raggiunge una soglia massima e l’oggetto in questione è piuttosto snello (snellezza λ=lunghezza libera d’inflessione l0/raggio d’inerzia ρ ). Ecco quindi che entrano in gioco altri parametri, dal momento che per progettare un’asta compressa si necessita di AREA e di INERZIA.
-Lunghezza asta
-Modulo di elasticita: E=210000 MPa
-Coefficiente di vincolo che ci dice come sbanda l’asta: β = 1
-Snellezza asta: l0/ρ = λ =  π √E/√fcd
-Raggio d’inerzia: ρ = l0/λ
-Momento d’inerzia: I = A*(ρ)2

In particolare effettuo il dimensionamento considerando il momento d’inerzia e il raggio d’inerzia.

Prendendo come esempio la prima riga, con un’area minima di 33,90 cm2, un raggio d’inerzia minimo di 3,18 cm e un momento d’inerzia minimo di 343 cm4, ho considerato sempre il profilo 219*5,9 (mm), notando che I_design=2247>I_min=343, che rho_min_design=7,54>rho_min=3,18 e che A_design=39,5>A_min=33,90.

Dato il solaio di carpenteria sopra raffigurato, eseguo il progetto della trave centrale maggiormente sollecitata di luce pari a 5 m con un impalcato in acciaio, uno in latero cemento e uno in legno. Il retino evidenziato rappresenta l'area d'influenza incidente sulla trave centrale (Area d'influenza=luce*interasse). Il dimensionamento tramite le tre tecnologie avviene considerando  1mc di solaio.

SOLAIO IN ACCIAIO:

I PASSAGGIO:

Calcolo il contributo del carico strutturale moltiplicando il volume dell'elemento per il suo peso specifico su un mq di solaio. Il peso specifico non è altro che il rapporto tra il peso di un campione di materiale e il suo volume.

Carico strutturale: getto di cls+lamiera grecata+travi secondarie IPE 160

Getto di cls: (0,06 * 1)[mc/mq] * 25[KN/mc] = 1,5[KN/mq]

Lamiera grecata: 7,85[Kg/mq]/100 = 0,078[KN/mq]

Travi secondarie IPE160: 2*(0,0020 * 1)[mc/mq] * 78,5[KN/mc] = 0,314[KN/mq]

II PASSAGGIO:

Calcolo il contributo del carico permanente non strutturale facendo le stesse operazioni applicate per il carico strutturale.

Carico permanente non strutturale: pavimento in gres porcellanato+massetto di livellamento+controsoffitto in cartongesso+1,5[KN/mq] (ovvero la somma degli impianti 0,5[KN/mq] e dei tramezzi 1[KN/mq])

Pavimento in gres porcellanato: (0,02 * 1 * 1)[mc/mq] * 20[KN/mc] = 0,4[KN/mq]

Massetto di livellamento: (0,04 * 1 * 1)[mc/mq] * 21[KN/mc] = 0,84[KN/mq]

Controsoffitto in cartongesso: (0,015 * 1 * 1)[mc/mq] * 13,25[KN/mc] = 0,2[KN/mq]

Considero inoltre il carico accidentale (carico variabile nel tempo) pari a 2[KN/mq]

III PASSAGGIO:

Trovo il carico strutturale totale: qs = 1,5+0,314+0,078 = 1,9[KN/mq]

Trovo il carico permanente non strutturale totale: qp = 0,4+0,84+0,2+1,5 = 2,94[KN/mq]

qa = 2[KN/mq]

IV PASSAGGIO:

Effettuo la combinazione fondamentale allo SLU, moltiplicando il totale dei carichi strutturali, permanenti non strutturali e variabili per dei coefficienti parziali di sicurezza considerati nella condizione più sfavorevole. Il coefficiente relativo a qs è 1,3, quello relativo a qp è 1,5 e quello relativo a qa è 1,5.

qtot  = (1,9*1,3)[KN/mq] + (2,94*1,5)[KN/mq] + (2*1,5)[KN/mq] = 9,88[KN/mq]

Poichè questo carico totale fa riferimento a quello distribuito su 1mq di solaio, per trovare il carico lineare agente sulla trave, devo calcolare il contributo del carico relativo all'area d'influenza incidente sulla trave sollecitata (qtot*A) e il risultato che ottengo lo divido per la luce della trave sollecitata.

A = L*i = 5[m]*4,75[m] = 23,5 mq

q(area d'influenza) = qtot*A = 9,88[KN/mq]*23,75[mq] = 234,65[KN]

qu(lineare) = (qtot*A)/L = 234,65[KN]/5[m] = 46,93[KN/m]

Questo risultato lo posso riscontrare nella tabella del file Excel, che mi effettua il calcolo automaticamente

V PASSAGGIO:

Sapendo che il Momento massimo di una trave doppiamente appoggiata di luce L è ql^2/8, calcolo il momento massimo della trave in esame = (qu(lineare)*L^2)/8 = =46,93[KN/m]*25[mq])/8 = 146,66[KN*m]

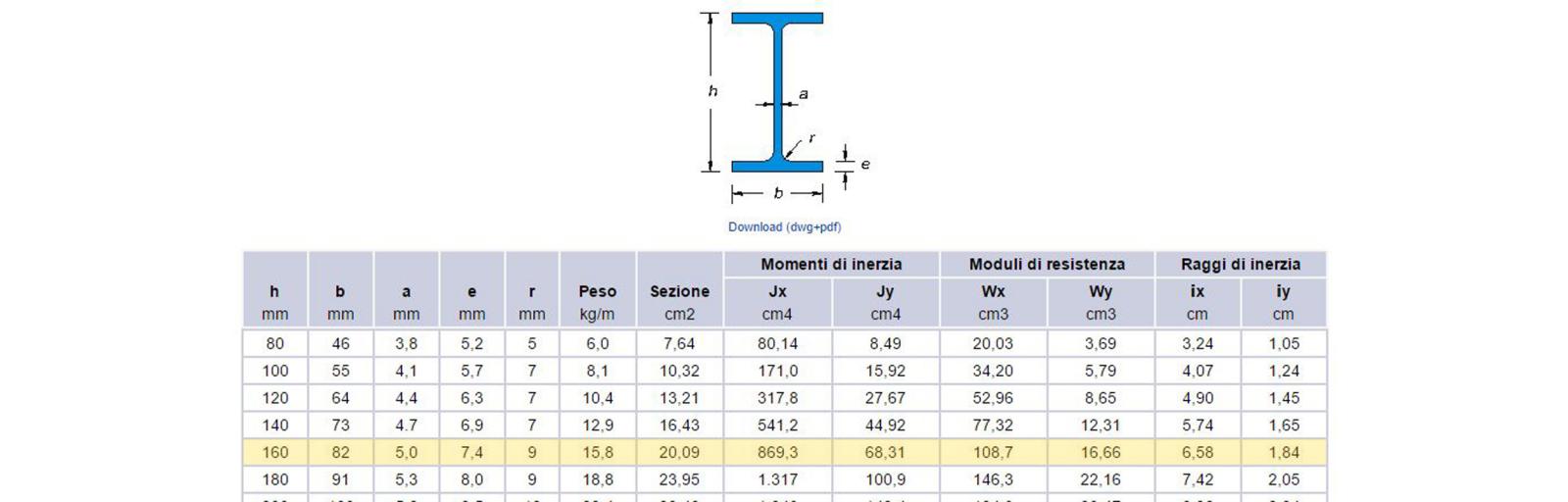
Ora scelgo acciaio S275 con fyk=275[N/mmq] = 27,5[KN/cmq] e fyd=27,5[KN/cmq]/1,05=26,19[KN/cmq] e mi trovo la resistenza minima di progetto  Wxmin=Mmax/fyd = 14666[KN/cm]/26,19 = 559,98[KN/cm]

Vado sul sagomario e scelgo un IPE con Wx >/= 559,98[KN/cm]

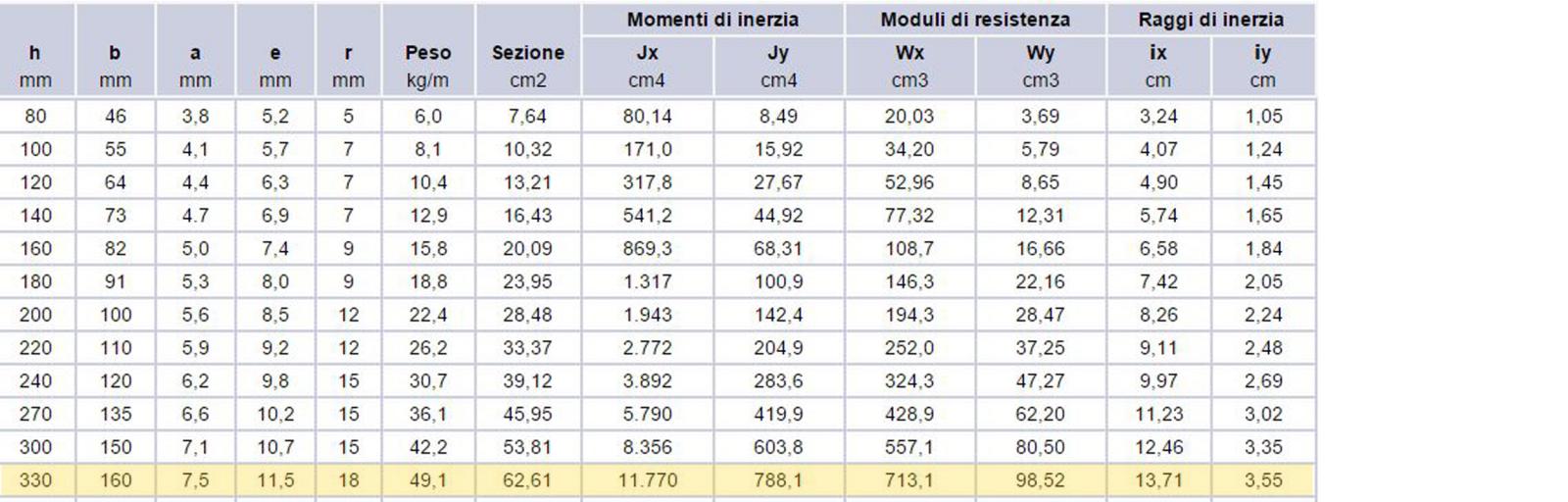IPE 330 -> Wx=713 cmc

Questi calcoli sono confermati dal foglio Excel

VI PASSAGGIO:

Aggiungo il peso della trave scelta al calcolo dei carichi strutturali, sapendo che il peso dell'IPE330 è di 49,1 [Kg/m]=0,49[KN/m]

qu= 9,88[KN/mq]*4,75[m] + 0,49[KN/m]*1,3 = 47,6[KN/m]

Ricalcolo Mmax=(47,6[KN/m]*25[m])/8= 148,6[KN*m]

Wxmin=14866[KN*cm]/26,19[KN/cmq]= 567,54[cmc] che è < 713 cmc

Quindi la scelta IPE330 è esatta e cambiando il dato qu nel foglio excel confermo la mia ipotesi

SOLAIO IN LATERO CEMENTO:

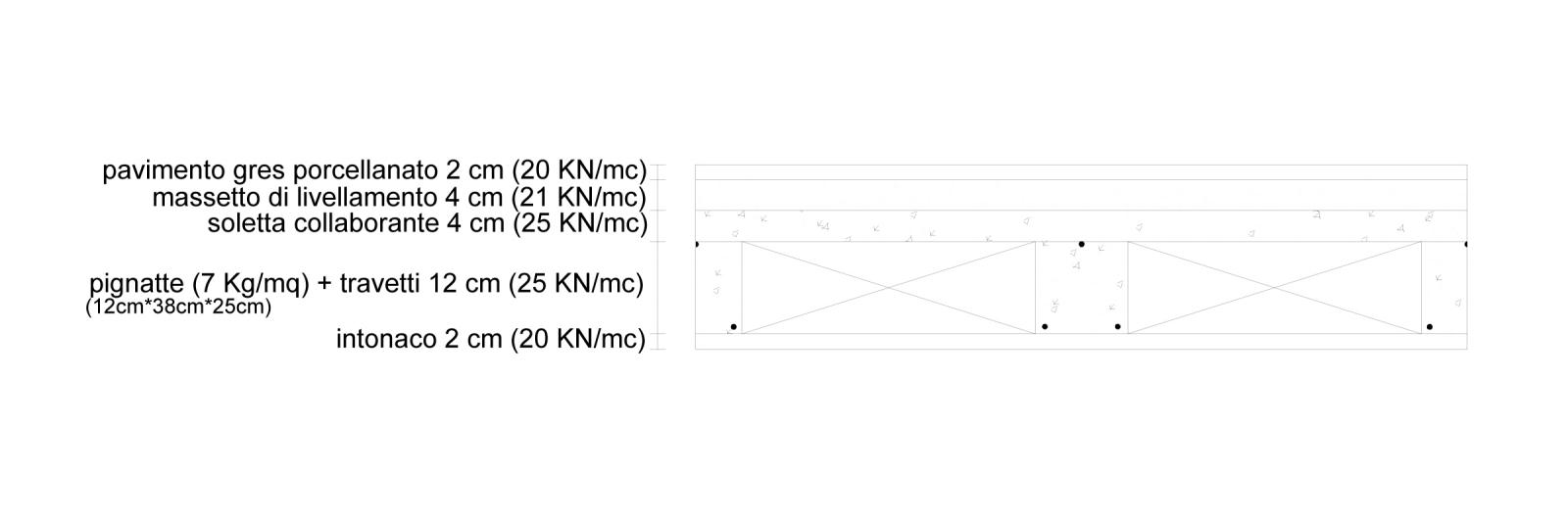
Nel progetto della trave in acciaio ho spiegato gradualmente i vari passaggi. Adesso li applico nuovamente andando più velocemente.

Carico strutturale: soletta collaborante+pignatte+travetti

Soletta collaborante: (0,04*1*1)[mc/mq] * 25[KN/mc] = 1[KN/mq]

Pignatte: 8*(7[kg/mq])=56[Kg/mq]= 0,56[KN/mq]

Travetti: 2*(0,12*0,12*1)[mc/mq] * 25[KN/mc]= 0,72[KN/mq]

Carico permanente non strutturale: pavimento in gres porcellanato+massetto di livellamento+intonaco

Pavimento in gres porcellanato: (0,02*1*1)[mc/mq] * 20[KN/mc] = 0,4[KN/mq]

Massetto di livellamento: (0,04*1*1)[mc/mq] * 21[KN/mc]= 0,84[KN/mq]

Intonaco: (0,02*1*1)[mc/mq] * 20[KN/mc]= 0,4[KN/mq]

Carico accidentale variabile

2[KN/mq]

Carico strutturale totale:

qs= 1+0,56+0,72=2,28[KN/mq]

Carico permanente non strutturale totale (con l'aggiunta di 1,5[KN/mq]):

qp= 0,4+0,84+0,4+1,5= 3,14[KN/mq]

Il carico totale qtot=qs*1,3+qp*1,5*qa*1,5=[50,7KN/mq]

Come possiamo notare, rispetto alla tabella dell'acciaio, come compaiano altri valori: questo è dettato dalla disomogeneità del materiale, poichè possiamo calcolare i due materiali (il cls compresso) e l'acciaio (teso) come due materiali con comportamento meccanico diverso tra loro. Per cui compaiono fyd che è la tensione allo snervamento dell'acciaio e fck che è la resistenza a compressione del calcestruzzo. Il tutto è intimamente legato, poichè come notiamo entrambe le resistenze occorrono per determinare l'altezza di progetto utile e totale di progetto. Ovviamente c'è un'ingenierizzazione finale che consiste nell'approssimare per eccesso l'altezza della trave per comodità costruttiva.

Sezione trave principale

SOLAIO IN LEGNO:

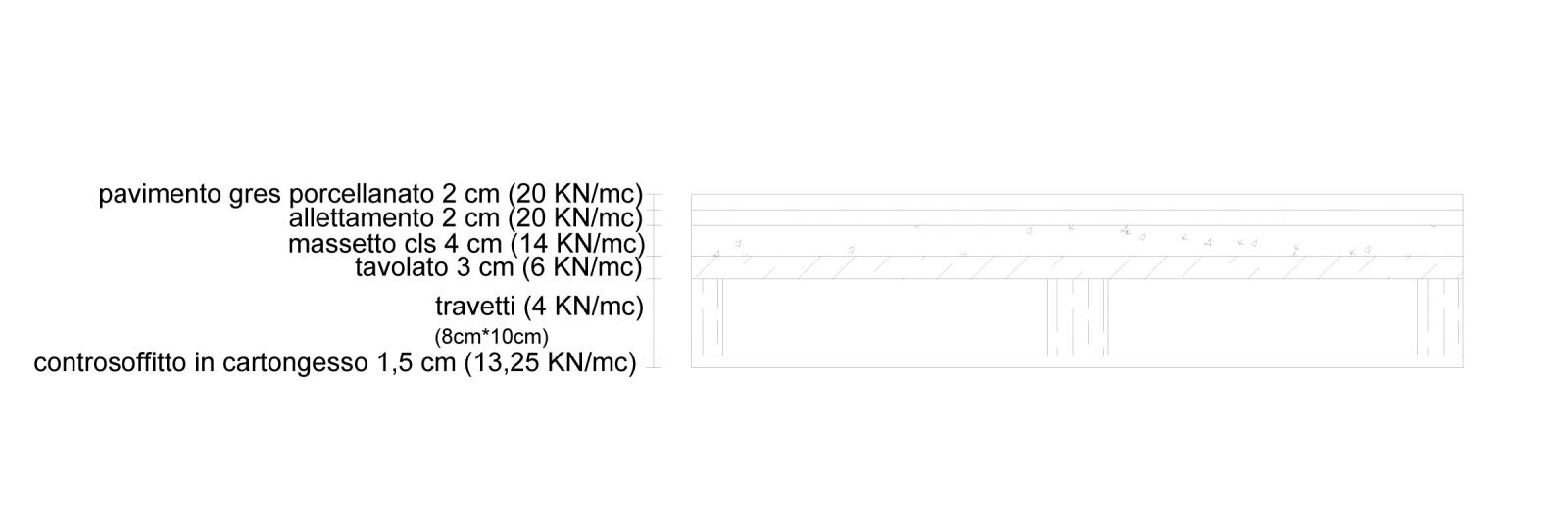Carico strutturale: tavolato+travetti

Travetti: 2*(0,08*0,1*1)[mc/mq] * 4[KN/mc] = 0,064[KN/mq]

Tavolato: (0,03*1*1)[mc/mq] * 6[KN/mc]= 0,18[KN/mq]

Carico permanente non strutturale: pavimento in gres porcellanato+massetto cls+allettamento+controsoffitto in cartongesso

Pavimento in gres porcellanato: (0,02*1*1)[mc/mq] * 20[KN/mc]=0,4[KN/mq]

Massetto in cls: (0,04*1*1)[mc/mq] * 14[KN/mc]= 0,56[KN/mq]

Allettamento: (0,02*1*1)[mc/mq] * 20[KN/mc]= 0,4[KN/mq]

Controsoffitto in cartongesso: (0,015*1*1)[mc/mq] * 13,25[KN/mc]= 0,2[KN/mq]

Carico accidentale variabile

2[KN/mq]

Carico strutturale totale:

qs= 0,064+0,18=0,24[KN/mq]

Carico permanente non strutturale totale (con l'aggiunta di 1,5[KN/mq]):

qp= 0,4+0,56+0,4+0,2+1,5= 3,06[KN/mq]

Il carico totale qtot=qs*1,3+qp*1,5*qa*1,5=[37,53KN/mq]

Per verificare se l'altezza ipotizzata, anche aggiungendo il peso proprio della trave risulti verificata, ho aggiunto ai carichi totali il peso proprio della trave moltiplicandolo per 1,3 (coeff. carichi strutturali) e la sezione risulta ugualmente verificata.

Sezione trave principale