La prima esercitazione consiste nel dimensionare a flessione una trave in: legno, acciaio e cemento di un telaio a nostra scelta.
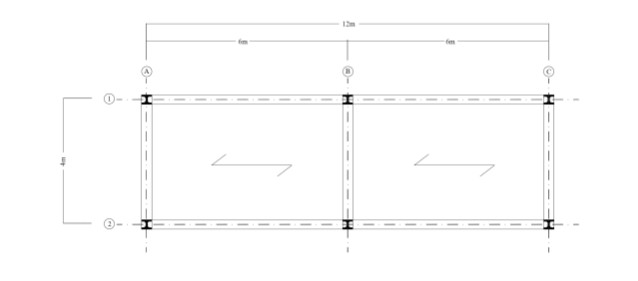
Il telaio utilizzato presenta due campate da 6 metri e luce di 4 metri.(per i solai in legno e cemento si prenda in considerazione la fig. 1; per il solaio in acciaio si prenda in considerazione la fig.2).
fig.1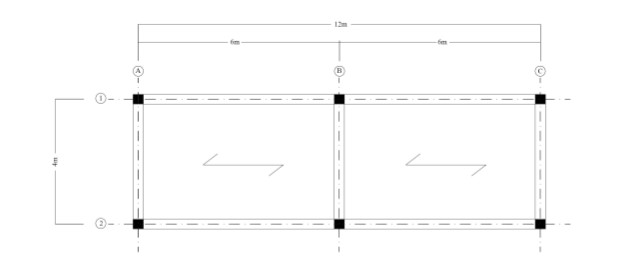
fig.2
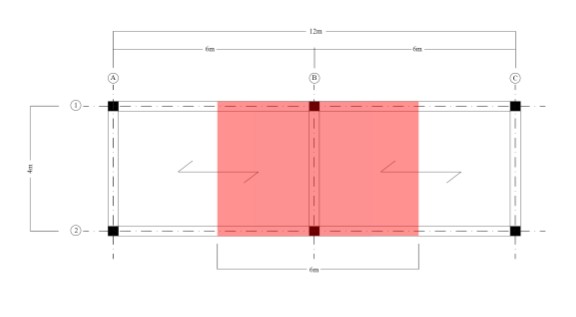
La trave sollecitata maggiormente è la trave B poiché presenta un'area di influenza maggiore (fig. 3) pari a 24mq derivanti dal prodotto I (6m) x L (4m); dove “I” rappresenta l'interasse e “L” rappresenta la luce.
fig.3
Dimensionamento di una trave in legno
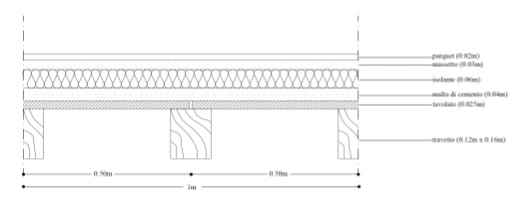
Elementi che compongono il solaio:
- Travetti 12 cm x 16 cm P= 0,6 T/mc = 6 KN/mc
- Tavolato 2,5 cm P= 0,6 T/mc = 6 KN/mc
- Malta di cemento 4 cm P= 21 KN/mq
- Isolante 6 cm P= 30 Kg/mc = 0,3 KN/mc
- Massetto 3 cm P= 1900 Kg/mc = 19KN/mc
- Parquet 2 cm P= 850 Kg/mc = 8,5 KN/mc
Calcolo dei carichi strutturali qs (escluso peso proprio della trave)
- Travetti
[2x(0,12m x 0,16m x 1m)/mq] x 6 KN/mc = 0,2304 KN/mq
- Tavolato
[(0,025m x 1m x 1m)/mq] x 6 KN/mc = 0,15 KN/mq
- Malta di cemento
[(0,04m x 1m x 1m)/mq] x 21 KN/mc = 0,84 KN/mq
qs= 0,2304 KN/mq + 0,15 KN/mq + 0,84 KN/mq = 1,2204 KN/mq
Calcolo dei carichi portati qp
- Isolante
[(0,06m x 1m x 1m)/mq] x 0,3 KN/mc = 0,018 KN/mq
- Massetto
[(0,03m x 1m x 1m)/mq] x 19 KN/mc = 0,57 KN/mq
- Parquet
[(0,02m x 1m x 1m)/mq] x 8,5 KN/mc = 0,17 KN/mq
- Impianti
0,5 KN/mq
- Tramezzi
1 KN/mq
qp= 0,018 KN/mq + 0,57 KN/mq + 0,17 KN/mq + 0,5 KN/mq + 1 KN/mq = 2,258 KN/mq
Calcolo dei carichi accidentali qa
La struttura è per un ambiente destinato ad un uso residenziale, quindi secondo normativa il carico accidentale sarà:
qa = 2,00 KN/mq
Dopo aver calcolato i vari carichi, inserisco i loro valori nel foglio excel, insieme ai dati dell' interasse e della luce del solaio.
Il momento massimo della trave calcolato sul foglio excel è dato dall' inserimento della formula Mmax equivalente a ql²/8 di una trave con doppio appoggio.
Per questo tipo di solaio il legno lamellare scelto ha una resistenza caratteristica a flessione di fm,k = 24 Mpa, dato inserito in tabella.
Successivamente inserisco la base della trave b = 30cm, e il foglio excel in maniera automatica attraverso il calcolo ( I x Mmax x 1000/ (b x fd)^0,5 ) calcola l'altezza minima della trave.

Avendo un hmin = 38,02 cm scelgo di ingegnerizzare l'altezza della trave a H= 40 cm.
Avrò quindi delle travi 30cm x 40cm, ma il calcolo è stato fatto senza tener conto del peso proprio della trave stessa; quindi per verificare che la sezione sia quella giusta calcolo il peso della trave e dopo averlo moltiplicato per 1,3 lo inserisco all'interno del valore qu che rappresenta il carico totale.
Pt = [(0,3m x 0,4m x 1m)/mq x 6 KN/mc] = 0,72 KN/mq
qu = [(qs x 1,3 + qp x 1,5 + qa x 1,5) + Pt x 1,3]

Dopo aver inserito il carico strutturale della trave si può notare come l'altezza minima sia uguale a 38,38 cm; quindi l'ipotesi di trave 30cm x 40cm è verificata.
Dimensionamento di una trave in acciaio
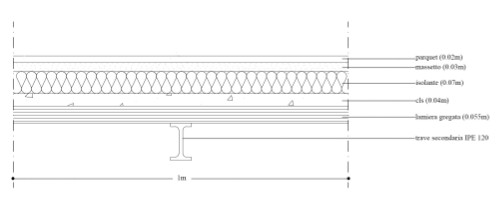
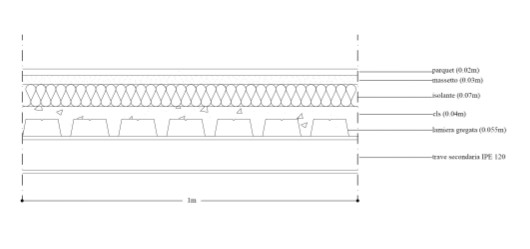
Elementi che compongono il solaio:
- Travi secondarie IPE 120 A= 13,20 cmq = 0,001320 mq P= 78 KN/mc
- Lamiera Grecata spessore = 1,2cm P= 15,70 Kg/mq = 0,1570 KN/mq
- Getto di cls 4 cm P= 24 KN/mc
- Isolante 7 cm P= 30 Kg/mc = 0,3 KN/mc
- Massetto 3 cm P= 1900 Kg/mc = 19 KN/mc
- Parquet 2 cm P= 850 Kg/mc = 8,5 KN/mc
Calcolo dei carichi strutturali qs (escluso peso proprio della trave)
- Travi secondarie IPE 120
[(0,001320mq x 1m)/mq x 78 KN/mc] = 0,10296 KN/mq
- Lamiera Grecata
0,1570 KN/mq
- Getto di cls + parte di riempimento della lamiera
[(0,0546mq x 1m)/mq x 24 KN/mc] = 1,3104 KN/mq
qs= 0,10296 KN/mq + 0,1570 KN/mq + 1,3104 KN/mq = 1,57036 KN/mq
Calcolo dei carichi portati qp
- Isolante
[(0,07m x 1m x 1m)/mq] x 0,3 KN/mc = 0,021 KN/mq
- Massetto
[(0,03m x 1m x 1m)/mq] x 19 KN/mc = 0,57 KN/mq
- Parquet
[(0,02m x 1m x 1m)/mq] x 8,5 KN/mc = 0,17 KN/mq
- Impianti
0,5 KN/mq
- Tramezzi
1 KN/mq
qp= 0,021 KN/mq + 0,57 KN/mq + 0,17 KN/mq + 0,5 KN/mq + 1 KN/mq = 2,261 KN/mq
Calcolo dei carichi accidentali qa
La struttura è per un ambiente destinato ad un uso residenziale, quindi secondo normativa il carico accidentale sarà:
qa = 2,00 KN/mq
Inserisco i valori dei carichi nel foglio excel, insieme ai dati dell' interasse e della luce del solaio. Prendo in considerazione la tensione caratteristica dell'acciaio scelto fyk= 275 Mpa, dalla tabella excel risulta un Wxmin pari a 386,36 cmc quindi scelgo un profilato IPE con un Wx direttamente superiore rispetto al valore trovato nonché IPE 270 con Wx= 429 cmc.

Per la scelta della trave non abbiamo tenuto conto del peso proprio di questa agente sui carichi strutturali, quindi verifichiamo che la scelta del profilato sia quella giusta.
Il peso della trave risulta
Pt= [(0,004590mq x 1m)/ mq x 78 KN/mc] = 0,35802 KN/mq
Inserisco il peso proprio della trave moltiplicato per 1,3 nella formula del carico totale qu.

Dalla figura si può notare come il valore del Wxmin sia variato = 389,92 cmc; perciò l'IPE 270 scelta inizialmente è verificata poiché il valore del suo Wx è superiore al Wxmin.
Dimensionamento di una trave in cemento armato
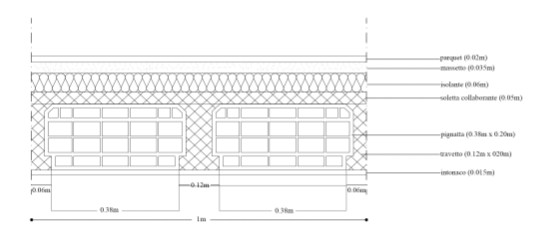
Elementi che compongono il solaio:
- Intonaco 1,5 cm P= 18 KN/mc
- Pignatta 38 cm x 20 cm x 25 cm n: 8 in 1mq P= 9,6 Kg
- Travetti 12 cm x 20 cm P= 24 KN/mc
- Soletta Collaborante 5 cm P= 24 KN/mc
- Isolante 6 cm P= 30 Kg/mc = 0,3 KN/mc
- Massetto 3,5 cm P= 1900 Kg/mc = 19 KN/mc
- Parquet 2 cm P= 850 Kg/mc = 8,5 KN/mc
Calcolo dei carichi strutturali qs (escluso peso proprio della trave)
- Pignatte
[(8 x 9,6 Kg)/ mq ] = 76,8 Kg/mq = 0,768 KN/mq
- Travetti
[2 x (0,12m x 0,20m x 1m)/mq x 24 KN/mc] = 1,152 KN/mq
- Soletta collaborante
[(0,05m x 1m x 1m)/mq x 24 KN/mc] = 1,2 KN/mq
qs= 0,768 KN/mq + 1,152 KN/mq + 1,2 KN/mq = 3,12 KN/mq
Calcolo dei carichi portati qp
- Intonaco
[(0,015m x 1m x 1m)/mq x 18 KN/mc] = 0,27 KN/mq
- Isolante
[(0,06m x 1m x 1m)/mq x 0,3 KN/mc] = 0,018 KN/mq
- Massetto
[(0,035m x 1m x 1m)/mq x 19 KN/mc] = 0,665 KN/mq
- Parquet
[(0,02m x 1m x 1m)/mq x 8,5 KN/mc] = 0,17 KN/mq
- Impianti
0,5 KN/mq
- Tramezzi
1 KN/mq
qp= 0,27 KN/mq + 0,018 KN/mq + 0,665 KN/mq + 0,17 KN/mq + 0,5 KN/mq + 1 KN/mq = 2,623 KN/mq
Calcolo dei carichi accidentali qa
La struttura è per un ambiente destinato ad un uso residenziale, quindi secondo normativa il carico accidentale sarà:
qa = 2,00 KN/mq
Inserisco i valori dei carichi nel foglio excel insieme ai valori di interasse e luce.
Scelgo un acciaio per le armature con un coefficiente di resistenza caratteristica pari a fyk = 450 Mpa e un calcestruzzo con resistenza caratteristica pari a fck = 25 Mpa.
Scelgo una base per la trave pari a 30 cm; il foglio excel calcola automaticamente l'altezza minima della mia trave pari a hmin = 49,70 cm; decido di ingegnerizzare l'altezza della trave a 55 cm.

Il calcolo è stato fatto senza tener conto del peso proprio della trave stessa; quindi per verificare che la sezione sia quella giusta calcolo il peso della trave e dopo averlo moltiplicato per 1,3 lo inserisco all'interno del valore qu.
Pt= [(0,30m x 0,55m x 1m)/mq x 24 KN/mc] = 3,96 KN/mq
aggiungo il valore del carico della trave moltiplicato per 1,3 a qu

Dopo aver inserito il peso proprio della trave possiamo notare come l'altezza minima sia variata da 49,70 cm a 51,41 cm; quindi la scelta iniziale di una trave delle dimensioni di 30 cm x 55 cm era giusta.
Commenti recenti