blog di Federica Mares

ESERCIZIO1_ trave semplice

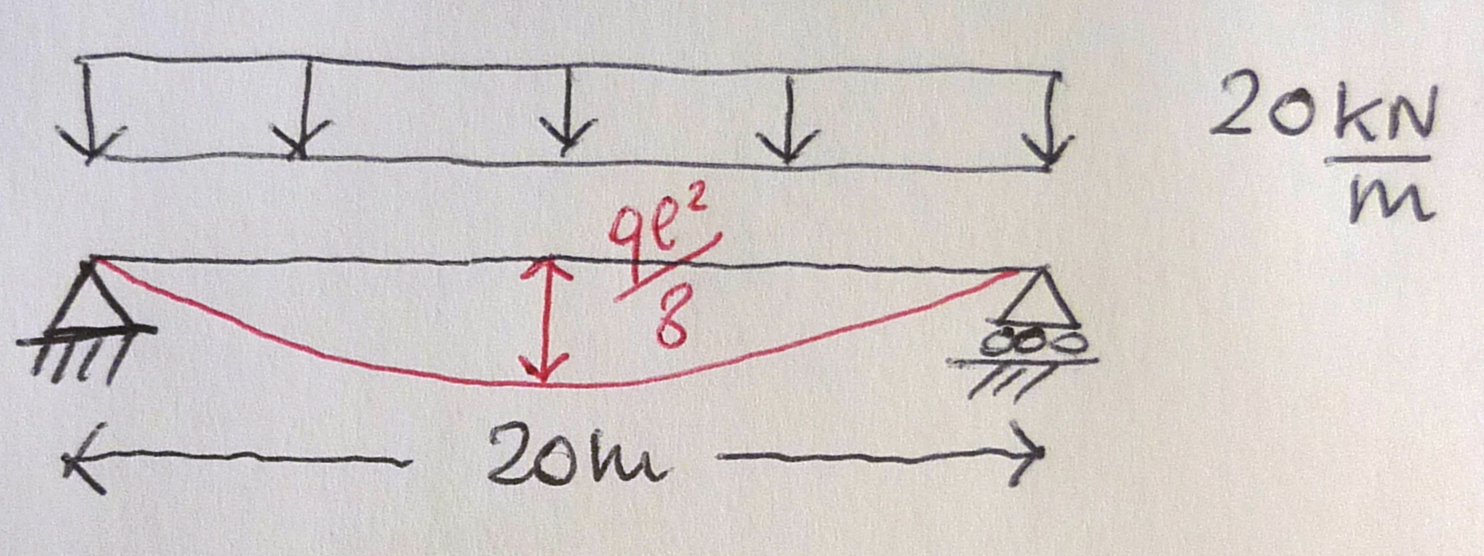
Il momento massimo è M=ql²/8quindi:

M_max= ql²/8 = [20 KN/m * (20 m)²] / 8 = 1000 KNm

 Per dimensionare la trave uso la formula W_x=M/σ_admconacciaio classeFe 360:

σ_adm = f_yk/ν = 235/1.2 = 195.3 N/mm²

Wx= M/σadm= 1000 KNm / [195.3 N/mm² *1000] = 0.0051 m³ --> 5100 cm³

 Dato che il valore di W_x è molto alto, aumento la σ_adm scegliendo l’acciaio classe Fe 510:

σ_adm= f_yk/ν= 355/1.2 = 295.83 N/mm²

W_x= M/σ_adm = 1000 KNm / [295.83 N/mm² *1000] = 0.0034 m³ --> 3400 cm³

Adotto una IPE O 600 (h=610 mm b=224 mm)Fe510 W_x=3879 cm³

ESERCIZIO2_ trave reticolare

Il carico distribuito da 20KN/m si divide sui 5 nodi in modo tale che i tre centrali siano soggetti a una forza puntuale di 100KN e quelli estremi di 50KN.

Analizzo la struttura con SAP per ottenere il valore di N_max a trazione (T) e di N_max a compressione (C).

Utilizzo il valore di T≈215 KN per progettare il tirante più sollecitato in acciaio classe Fe510:

A_min= T/σ_adm = [215 KN*1000]  / 295.83 N/mm² = 726.77 m²= 7.3 cm²

Risulta necessario un profilo tubolare a sezione circolare con diametro d=76.1 mme spessore s=3.2 mm.

Utilizzo il valore di C≈200 KN per progettare il puntone più sollecitato in acciaio classe Fe510:

I_min= (C*ν*l²)/(π²*E)= [200 KN*1.2*(500cm)²]  / (π²*2100 N/cm²) = 289.49 cm⁴

Risulta necessario un profilo tubolare a sezione circolare con momento di inerzia I=293 cm⁴, diametro d=127 mm e spessore s=4 mm.

A questo punto calcolo la snellezza λ = lo / ρ_min:

ρ= √ I / A = √ 293/15,5 = 4,34 cm

λ= 500/4,34 = 115,2

 Adotto per i tiranti un profilo tubolare circolare d=76.1 mm

e per i puntoni un profilo tubolare circolare d=127 mm

ESERCIZIO3 _ trave Vierendeel

Analizzo la struttura con SAP per ottenere il momento massimo M_max=230.3 KNm dopo aver imposto la rigidezza delle travi uguale a 1 e dei pilastri pari a 1000.

A questo punto posso progettare la trave di acciaio classe Fe510:

W_x= M/σ_adm = 230.3 KNm / [295.83 N/mm² *1000] = 0.00078 m³ --> 780 cm³

 Adotto una IPE 360 (h=360 mm b=170 mm)Fe510 W_x=904 cm³

CONCLUSIONI

Per superare una luce di 20m e sostenere un carico distribuito di 20KN/m è preferibile adottare una trave Vierendeel perché consente di risparmiare sul materiale e ha un’altezza minore, quindi risponde ai requisiti meglio delle altre due tipologie.

Disegno le 3 possibili deformate dei piani dovute all’azione delle 3 forze e considero le sollecitazioni di taglio che agiscono sui pilastri e sui traversi.

Bilanciando le forze sul traverso del terzo piano la forza che agisce è pari alla somma dei tagli moltiplicata per lo spostamento.

F= 4 (12EI/h³) δ3 = (48EI/h³)δ3

δ3= Fh³/48EI --> T = (12EI/h³)*( Fh³/48EI) = F/4

M= (6EI/h²)*( Fh³/48EI) = Fh/8

 Sul traverso del secondo piano agisce sempre una forza verso destra però di intensità doppia, quindi lo spostamento δ2 sarà maggiore e pari a:

δ2= Fh³/12EI --> T = (12EI/h³)*( Fh³/12EI) = F

M= (6EI/h²)*( Fh³/12EI) = Fh/2

Sul traverso al piano terra agisce le sollecitazioni di taglio T=F dei tre pilastri superiori che bilanciano la forza applicata a destra --> 3T = 3F --> δ2 = 0

Quindi i pilastri a terra non presentano taglio: l’altezza del terzo pilastro è ininfluente rispetto al calcolo della sollecitazione e del momento visto che il taglio sul traverso e la forza applicata sono uguali.

VERIFICA SAP

Dopo aver trovato i valori di δ1, δ2 e δ3 posso calcolare i momenti dei pilastri con la formula

M = (6EI/l²)*δ

δ1= Fl³/12EI --> M = (6EI/l²)*( Fl³/12EI) = Fl/2

δ2= 0 --> M = 0

δ3= Fl³/36EI --> M = (6EI/l²)*( Fl³/36EI) = Fl/6

 Il momento massimo è sui pilastri al primo piano, il secondo livello non si sposta (δ2= 0) quindi ha momento nullo, all’ultimo piano arriva un terzo del momento massimo.

ESERCIZIO 2

La struttura è due volte iperstatica e scelgo come incognita il valore di x, cioè la forza di trazione o compressione cui è sottoposta l’asta BD.

Le due strutture isostatiche che analizzerò sono la mensola con carico distribuito q e forza concentrata xsull’estremo libero e la trave appoggiata con carico distribuito q e forza concentrata xin mezzeria.

Lo spostamento dei punti B e D deve essere lo stesso, quindi V(B) = V(D).

Nel punto B V(B) è dato dalla somma del contributo del carico q e quello della forza concentrata x.

V(B)  = ql^4/8EI- xl³/3EI

Nel punto D lo spostamento V(C) è dato dal contributo del carico q e dalla forza concentrata x.

V(D)  =5ql^4/384EI- xl³/48EI

Il diagramma del momento è dato dalla sovrapposizione del momento della mensola con carico distribuito e di quella con forza concentrata sull’estremo libero. Lo stesso vale per la seconda struttura isostatica: il momento della iperstatica è somma del momento della trave appoggiata con carico distribuito e quello della trave con carico concentrato in mezzeria.

Ho analizzato su SAP la struttura con luce l=3, carico distribuito q=100 KN/m e forza concentrata

x =(43*100*3)/136 = 94,86 KN. I calcoli sono corretti.

La prima esercitazione l’ho postata il 3/04/2011 come commento al mio primo intervento sul blog, perché ancora non avevo capito come postare sul sito.

ESERCIZIO 1

La struttura è due volte iperstatica, quindi devo considerare la rotazione relativa nei punti B e C per trovare i valori delle incognite iperstatiche x1e x2, corrispondenti al valore dell’azione di contatto momento in quei punti.

Per semplificare i calcoli, sostituisco lo sbalzo della mensola con il momento corrispondente ql²/8 (sarebbe ql²/2, ma la luce è l/2).

Nel punto B la rotazione relativa Δφ(B)è data dal contributo di rotazione φdato dal carico q, dal momento della mensola, dalla rotazione x’  in B e x”in C e deve risultare nulla.

Δφ(B) =ql³/12EI – ql³/48EI– 2x’l/3EI– x”l/6EI= 0

Nel punto C la rotazione relativa Δφ(C)è data dal contributo di rotazione φdato dal carico q, dalla rotazione x’  in B e x”in C e deve risultare nulla.

Δφ(C) =ql³/12EI– 2x’l/3EI– x”l/6EI= 0

Dalla formula di Δφ(C) ricavo x’, lo sostituisco inΔφ(B) e trovo il valore dix”.

A questo punto posso disegnare il diagramma del momento come somma di due strutture: la prima con le cerniere e il carico, la seconda con i momenti sugli appoggi senza carico.

Ho verificato la correttezza dei calcoli si SAP definendo una struttura con luce l=3m e carico q=100 KN/m. I calcoli e i diagrammi risultano giusti.

...cancro!

Allego la foto dei calcoli dell'analisi dimensionale della curvatura... 1/[L]

...cancro!

Allego la foto dei calcoli dell'analisi dimensionale della curvatura... 1/[L]