blog di Federica Paolucci

Dovendo superare una luce di 20 m con una carico distribuito di 20 kN/m i tre esercizi riportati di seguito mostrano le differenti sezioni che può assumere una trave in base alla sua tipologia.

ESERCIZIO 1 | Trave appoggiata

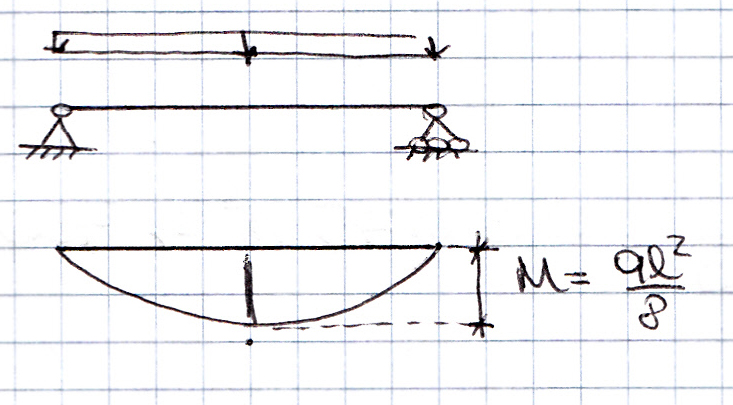
Sapendo che il momento massimo è M_max = ql²/8 = 20 * 20² /8 = 1.000 kN*m

Quindi attraverso la formula che ci fornisce il modulo di resistenza:

W_min = M_max/σ_am con σ_am = σ_c / υ

Ottengo:

σ_am = 235/1,15 = 204,35 MPa

W_min = 1.000/204,35*1000 = 0,005 m³ = 5.000 cm³

Non avendo trovato tra i profili un’IPE con un modulo di resistenza soddisfacente provo utilizzando un acciaio più resistente:

σ_am = 355/1,15 = 308,7 MPa

W_min = 1.000/308,7*1.000 = 0,0033 m³ = 3.300 cm³

Nonostante questa modifica non si ottiene un riscontro adeguato tra i profili standard.

ESERCIZIO 2 | Trave reticolare

Sapendo che il carico distribuito q = 20 kN/m ottengo, in base alle zone di influenza, un carico puntuale F₁ = 100 kN nei tre nodi centrali e un carico di F₂ = 50 kN nei nodi estremi.

Calcolando le sollecitazioni con SAP ottengo i valori delle forze assiali che agiscono sulle aste. Il puntone più sollecitato ha N_C = 200 kN (ca.) mentre il tirante più sollecitato ha N_T = 215 kN (ca.)

Progetto del tirante:

A_min = N_T / σ_am = 215*1.000/308,7 = 696,5 mm² = 6,965 cm²

Ottengo così un profilo tubolare a sezione circolare con diametro d = 76,1 mm e spessore s = 3,2 mm

Progetto del puntone:

I_min = N_C * υ* lo² / π² * E  

dove E è il modulo elastico dell’acciaio pari a E = 2.100.000 kg/cm² e lo è la lunghezza equivalente che in questo caso è uguale a quella reale.

Quindi I_min = 200*1,15*(5²*10⁴)/π²*21.000 = 277,5 cm⁴

Ottengo così un profilo tubolare a sezione circolare con diametro d = 127 mm, spessore s = 4 mm, momento di inerzia I = 293 cm^4 e sezione A = 15,5 cm^2

Posso così calcolarmi la snellezza:

λ = lo / ρ_min

ρ = √ I / A = √ 293/15,5 = 4,34 cm

λ = 500/4,34 = 115,2

ESERCIZIO 3| Trave Vierendeel

Ottenuto il momento massimo con SAP pari a M_max = 230,3 kN*m, avendo utilizzato rigidezza nelle travi pari a 1 e nei pilastri pari a 1.000, posso calcolare il modulo di resistenza:

W_min = M_max / σ_am = 230,3/308,7*1.000 = 0,00075 m³ = 750 cm³

Adotto quindi un profilo IPE 360 con h = 360 mm, b = 170 mm e Wx = 904 cm³

Posso quindi notare come le tre tipologia di travi richiedano, a parità di condizioni e materiale, altezze differenti. La trave appoggiata risulta essere tra le tre la soluzione più svantaggiosa.

ESERCIZIO

Come primo passaggio ipotizzo la deformata, partendo sempre dal basso verso l’alto. Man mano che la disegno identifico δ sapendo che δ₁ deforma il piano terra, e trascina quelli sopra. Quindi δ₂ sarà la deformazione del primo piano mentre il terzo si sposta orizzontalmente di δ₁ + δ₂ e si deforma di δ₃.

Usando come modello di riferimento una trave doppiamente incastrata che ha un cedimento δ determino il taglio che agisce su ogni traverso.

Posso quindi definire le equazioni di equilibrio alla traslazione orizzontale dei traversi:

1)    F = (4 x 12EI/h^3) x δ₃

Da cui ottengo δ₃ = Fh^3/48EI

E quindi T = 12EI/h^3 x Fh^3/48EI = F/4

2)    2F = (4 x –F/4) + [(3 x 12EI/h^3) x δ₂]

Da cui ottengo δ₂ = Fh^3/12EI

E quindi T = 12EI/h^3 x Fh^3/12EI = F

3)    -3F +3F = (2 x 12EI/h^3) x δ₁ + 12EI/(h/2)^3 x δ₁

Da cui ottengo δ₁ = 0

E quindi T = 0

Sapendo che per questo modello di trave il momento è M = 6EI/h^3 x δ ottengo i momenti:

1. M =6EI/h^3 x Fh^3/48EI = Fh/8
2. M = 6EI/h^3 x Fh^3/12EI = Fh/2
3. M = 0

Sap 2000

Imposto l'esercizio su Sap inserendo h=2m e F=100kN

Inserisco nuovamente la seconda esercitazione perchè si è cancellata dal blog.

ESERCIZIO 1

La struttura presa in esame è 2 volte iperstatica quindi per poterne studiare la deformazione le conferisco 2 GdL consentendo la rotazione relativa nei punti B e C. Così facendo posso trovare il valore dell’azione esercitata dai vincoli in B e C, rispettivamente x₁ e x₂.

Inoltre per semplificare il calcolo sostituisco la mensola con il momento da essa prodotto: q(l/2)^2/2 = ql^2/8 

Punto B: la rotazione relativa Δφ_B = Δφ_Bs - Δφ_Bd = 0

Δφ_B = ql^2/16 -2x₁/3 –x₂/6 = 0

Punto C:la rotazione relativa Δφ_C = Δφ_Cs – Δφ_Cd = 0

Δφ_C = ql^2/12 -x₁/6 –2x₂/3 = 0

Mettendo a sistema le equazioni delle rotazioni relative ottengo x₁ e x₂:

x1 = ql^2/15

x2 = 13ql^2/120

ESERCIZIO 2

La struttura presa in esame è 1 volta iperstatica quindi per poterne studiare la deformazione le conferisco 1 GdL sostituendo l’asta BD con x, supponendo l’asta tesa. In questo modo ottengo due strutture isostatiche: la mensola con carico distribuito q e forza concentrata all’estremo B, x, e la trave appoggiata con carico distribuito q e forza concentrata in mezzeria x.

Dobbiamo porre come condizione v_B = v_C poiché abbiamo eliminato l’asta ma teniamo in considerazione la sua azione: impedisce l’allontanamento e l’avvicinamento dei punti B e D.

Punto B:lo spostamento relativo v_B = v_B(q) + v_B(x)

v_B = ql^4/8EI – xl^3/3EI

Punto D: lo spostamento relativo v_D = v_D(q) + v_D(x)

v_D = 5ql^4/384EI + xl^3/48EI

Posto v_B = v_C ottengo: x = 43ql^2/136

...Acquario