Metodo delle forze

Inserisco nuovamente la seconda esercitazione perchè si è cancellata dal blog.

ESERCIZIO 1

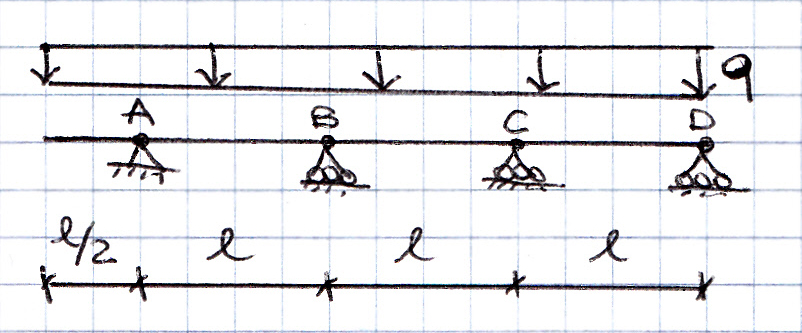
La struttura presa in esame è 2 volte iperstatica quindi per poterne studiare la deformazione le conferisco 2 GdL consentendo la rotazione relativa nei punti B e C. Così facendo posso trovare il valore dell’azione esercitata dai vincoli in B e C, rispettivamente x₁ e x₂.

Inoltre per semplificare il calcolo sostituisco la mensola con il momento da essa prodotto: q(l/2)^2/2 = ql^2/8 

Punto B: la rotazione relativa Δφ_B = Δφ_Bs - Δφ_Bd = 0

Δφ_B = ql^2/16 -2x₁/3 –x₂/6 = 0

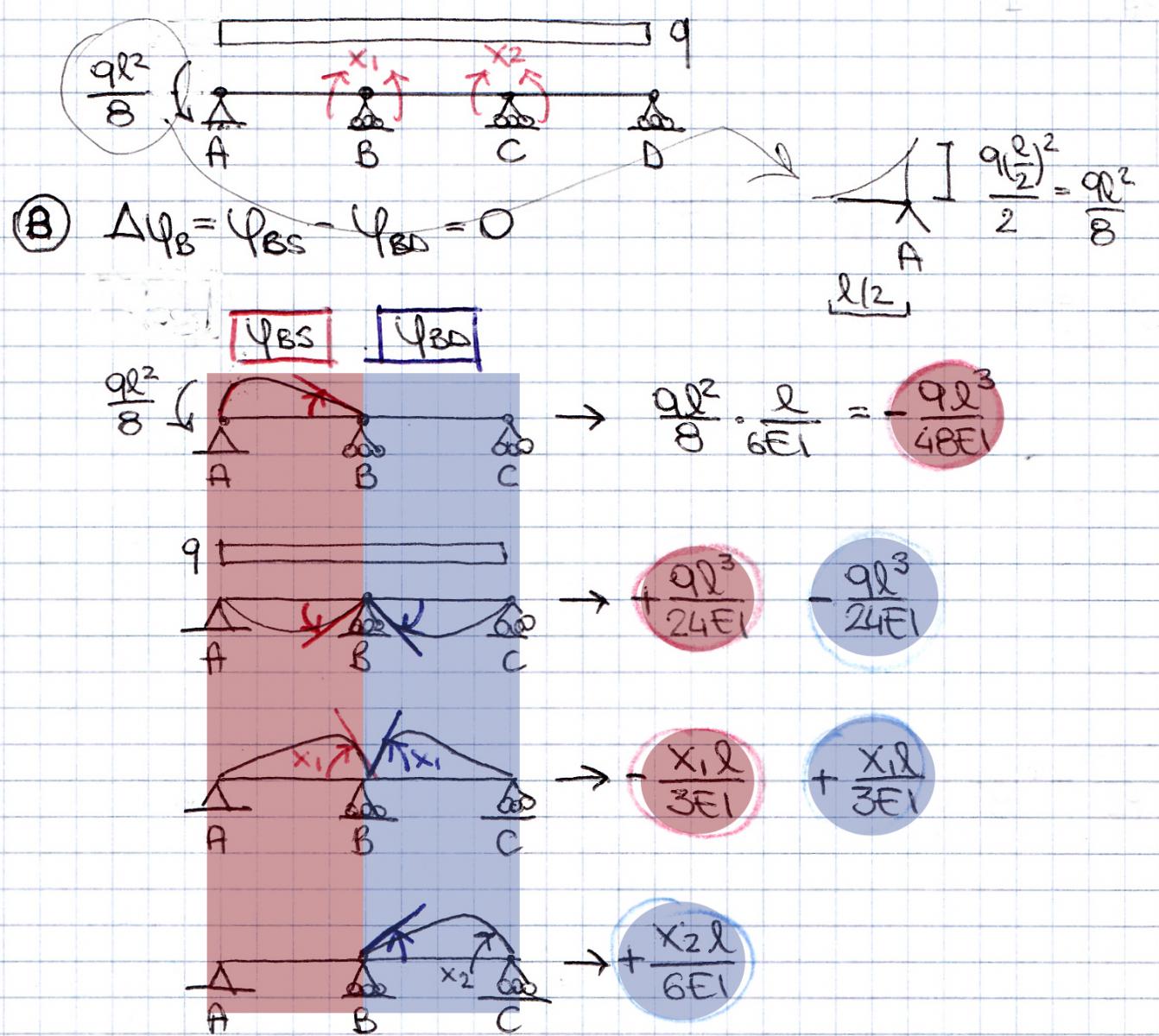
Punto C:la rotazione relativa Δφ_C = Δφ_Cs – Δφ_Cd = 0

Δφ_C = ql^2/12 -x₁/6 –2x₂/3 = 0

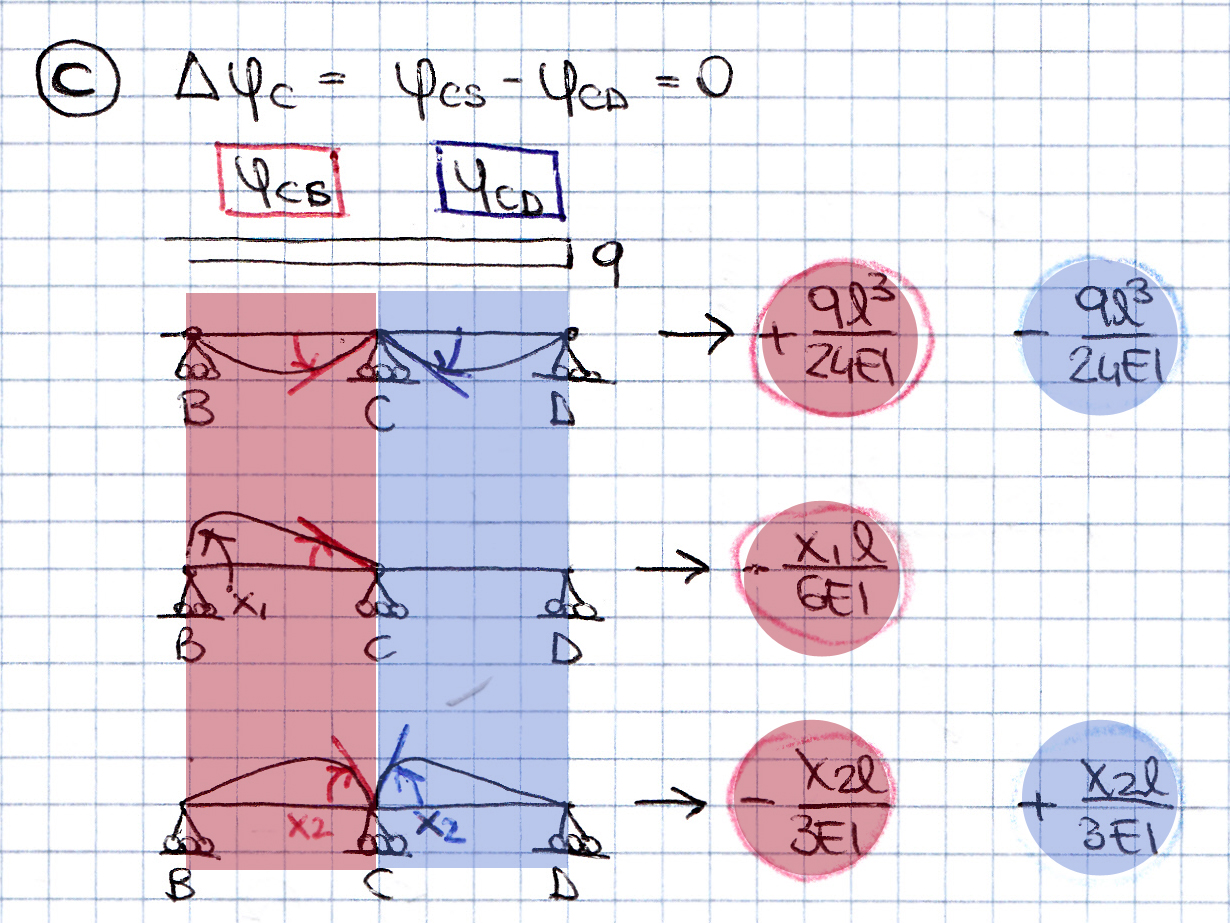
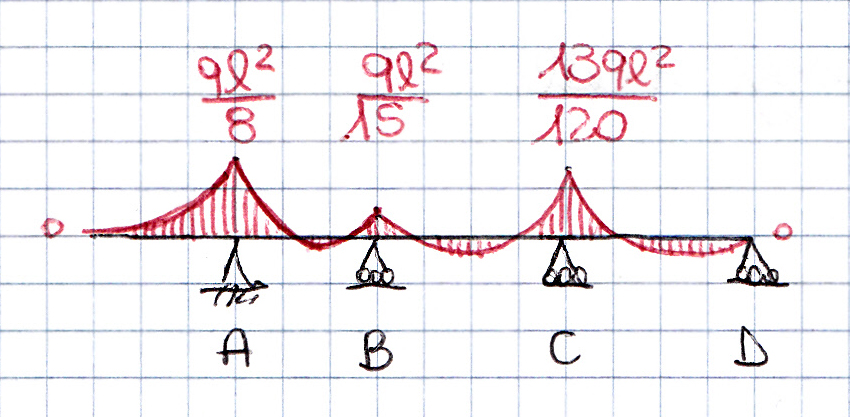
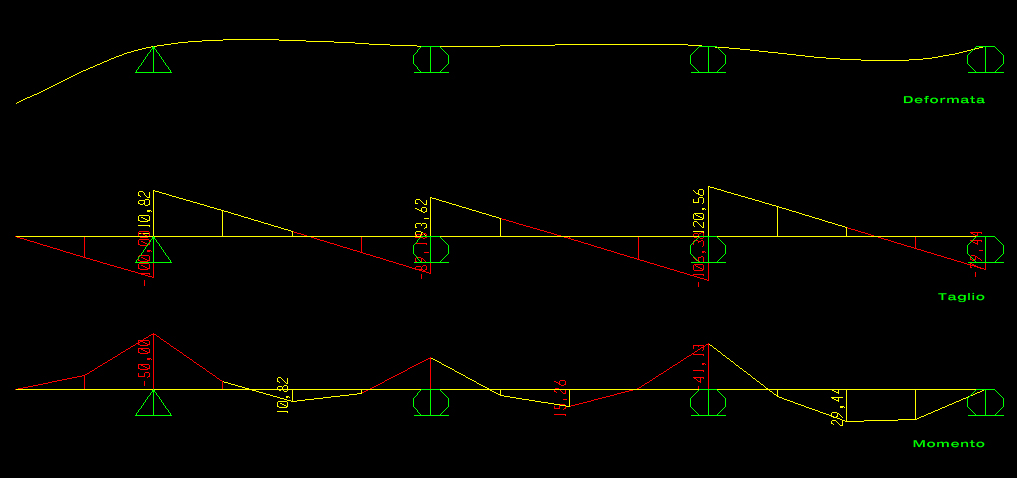
Mettendo a sistema le equazioni delle rotazioni relative ottengo x₁ e x₂:

x1 = ql^2/15

x2 = 13ql^2/120

ESERCIZIO 2

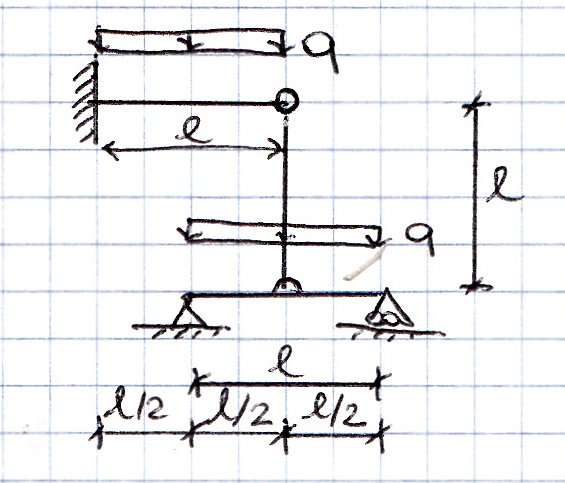
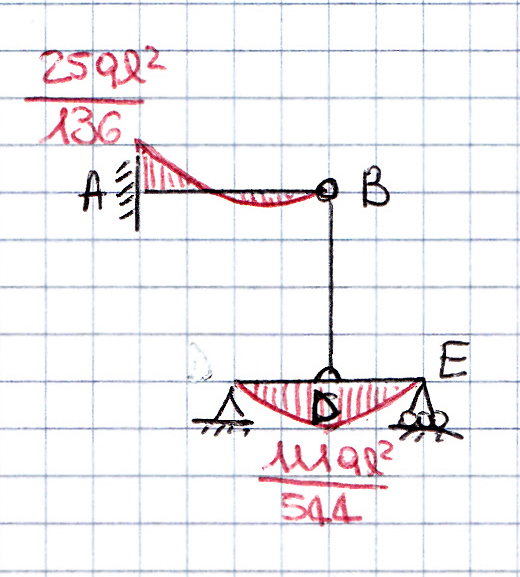
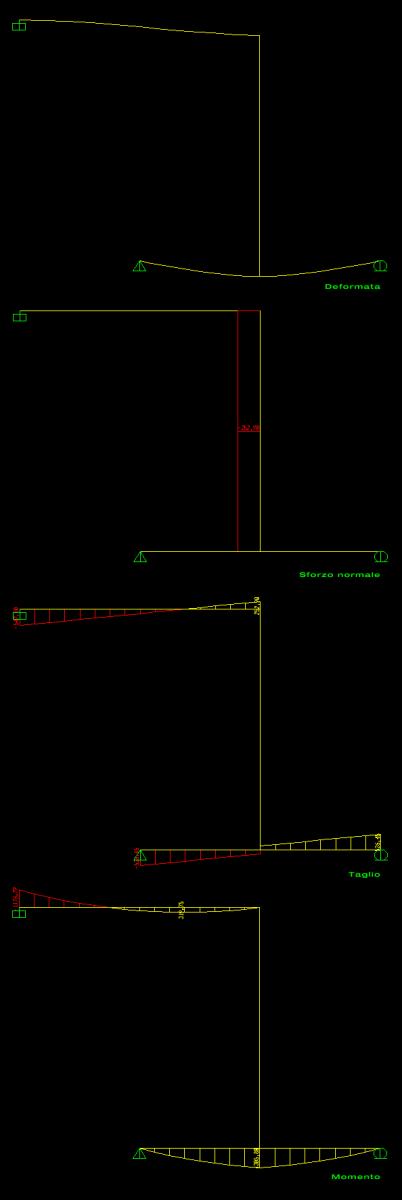
La struttura presa in esame è 1 volta iperstatica quindi per poterne studiare la deformazione le conferisco 1 GdL sostituendo l’asta BD con x, supponendo l’asta tesa. In questo modo ottengo due strutture isostatiche: la mensola con carico distribuito q e forza concentrata all’estremo B, x, e la trave appoggiata con carico distribuito q e forza concentrata in mezzeria x.

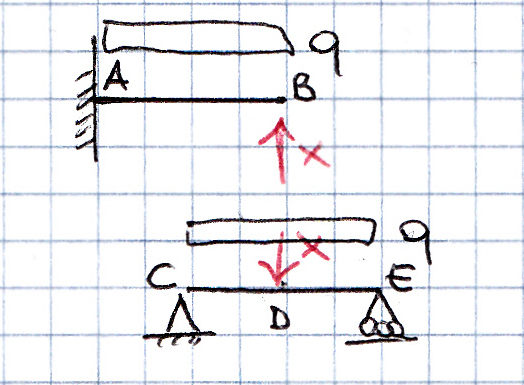
Dobbiamo porre come condizione v_B = v_C poiché abbiamo eliminato l’asta ma teniamo in considerazione la sua azione: impedisce l’allontanamento e l’avvicinamento dei punti B e D.

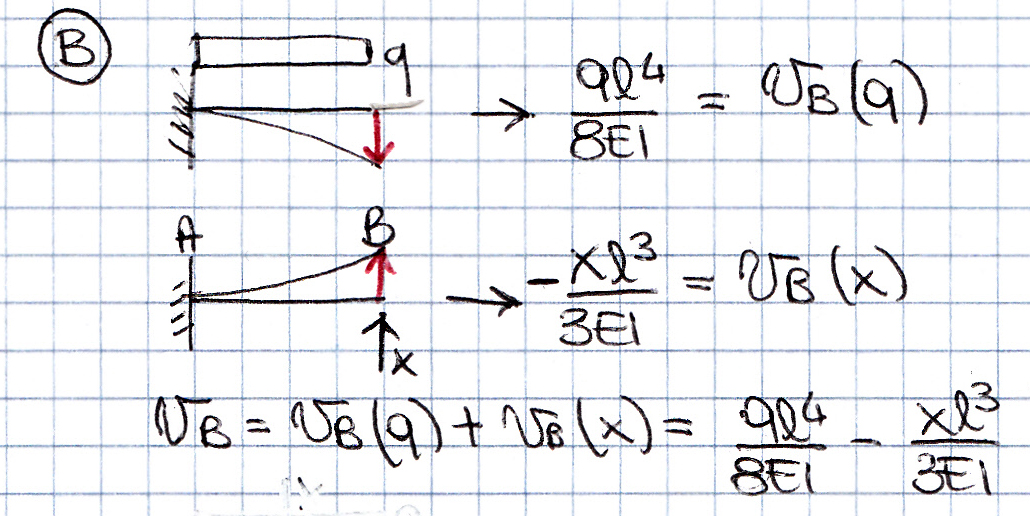
Punto B:lo spostamento relativo v_B = v_B(q) + v_B(x)

v_B = ql^4/8EI – xl^3/3EI

Punto D: lo spostamento relativo v_D = v_D(q) + v_D(x)

v_D = 5ql^4/384EI + xl^3/48EI

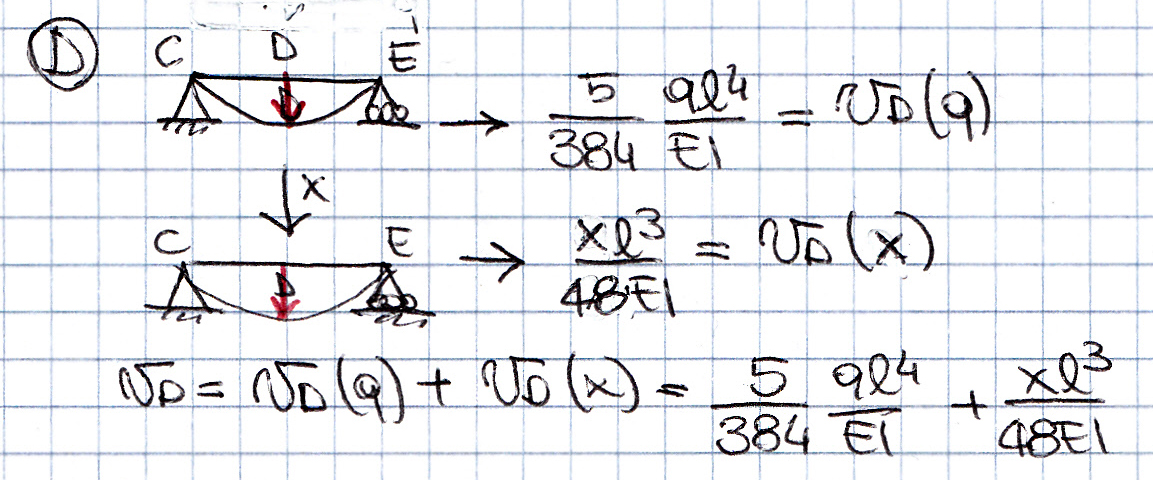
Posto v_B = v_C ottengo: x = 43ql^2/136