Telaio Shear Type

ESERCIZIO

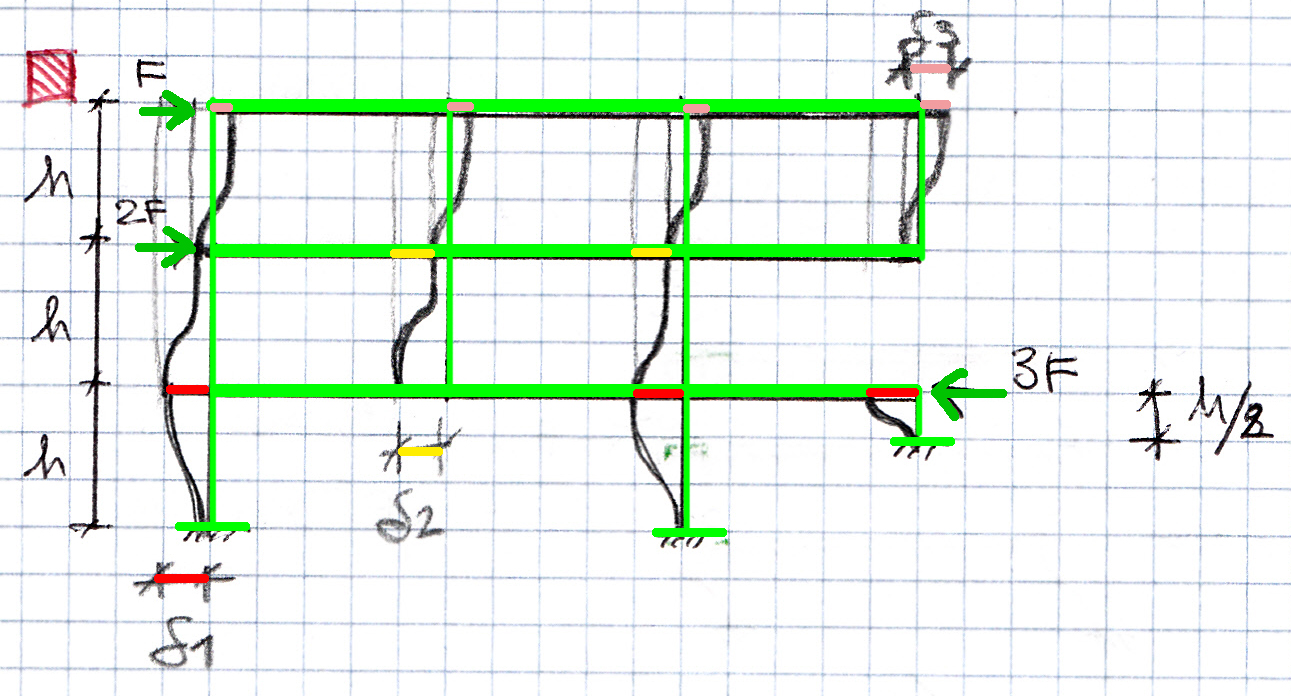
Come primo passaggio ipotizzo la deformata, partendo sempre dal basso verso l’alto. Man mano che la disegno identifico δ sapendo che δ₁ deforma il piano terra, e trascina quelli sopra. Quindi δ₂ sarà la deformazione del primo piano mentre il terzo si sposta orizzontalmente di δ₁ + δ₂ e si deforma di δ₃.

Usando come modello di riferimento una trave doppiamente incastrata che ha un cedimento δ determino il taglio che agisce su ogni traverso.

Posso quindi definire le equazioni di equilibrio alla traslazione orizzontale dei traversi:

1)    F = (4 x 12EI/h^3) x δ₃

Da cui ottengo δ₃ = Fh^3/48EI

E quindi T = 12EI/h^3 x Fh^3/48EI = F/4

2)    2F = (4 x –F/4) + [(3 x 12EI/h^3) x δ₂]

Da cui ottengo δ₂ = Fh^3/12EI

E quindi T = 12EI/h^3 x Fh^3/12EI = F

3)    -3F +3F = (2 x 12EI/h^3) x δ₁ + 12EI/(h/2)^3 x δ₁

Da cui ottengo δ₁ = 0

E quindi T = 0

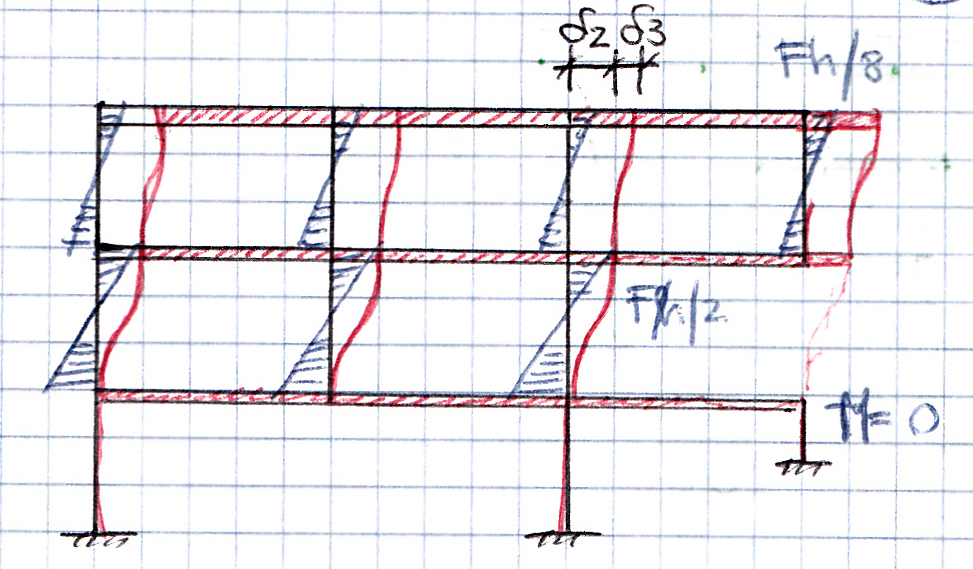
Sapendo che per questo modello di trave il momento è M = 6EI/h^3 x δ ottengo i momenti:

1. M =6EI/h^3 x Fh^3/48EI = Fh/8
2. M = 6EI/h^3 x Fh^3/12EI = Fh/2
3. M = 0

Sap 2000

Imposto l'esercizio su Sap inserendo h=2m e F=100kN