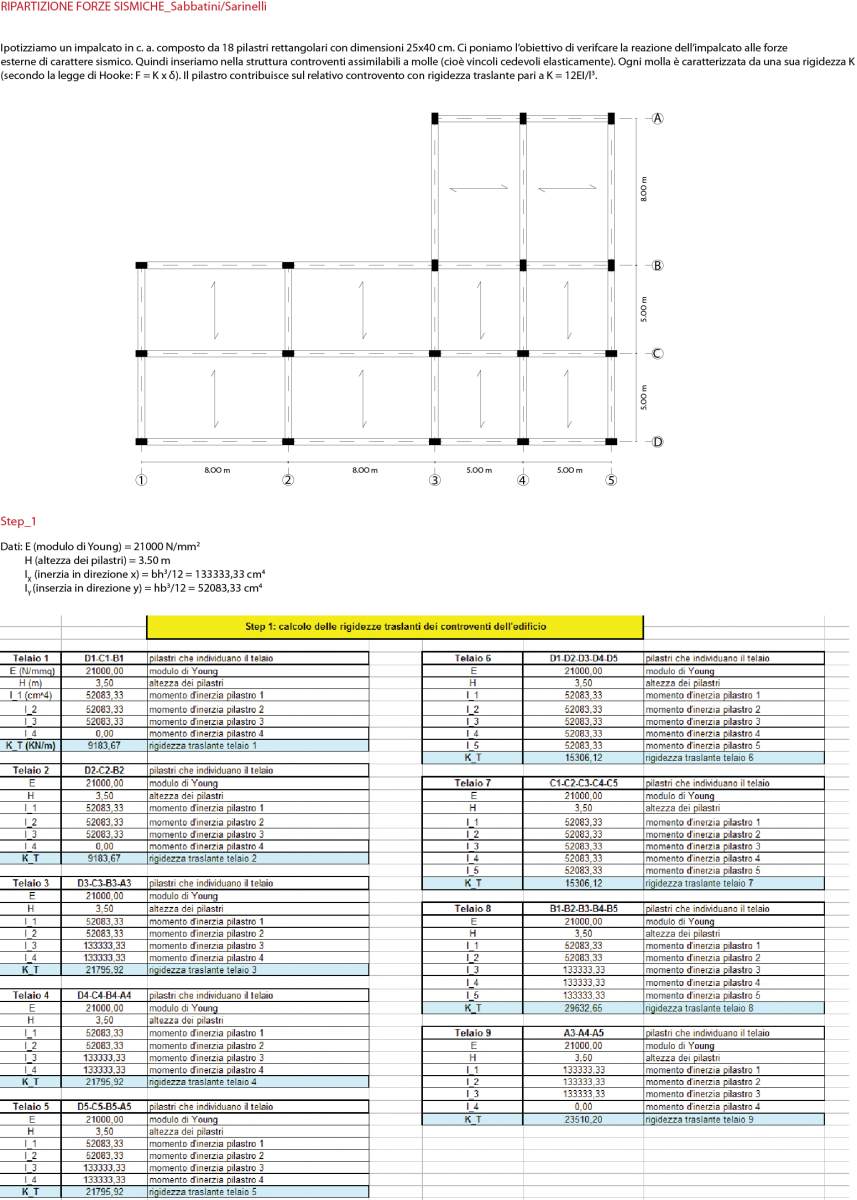
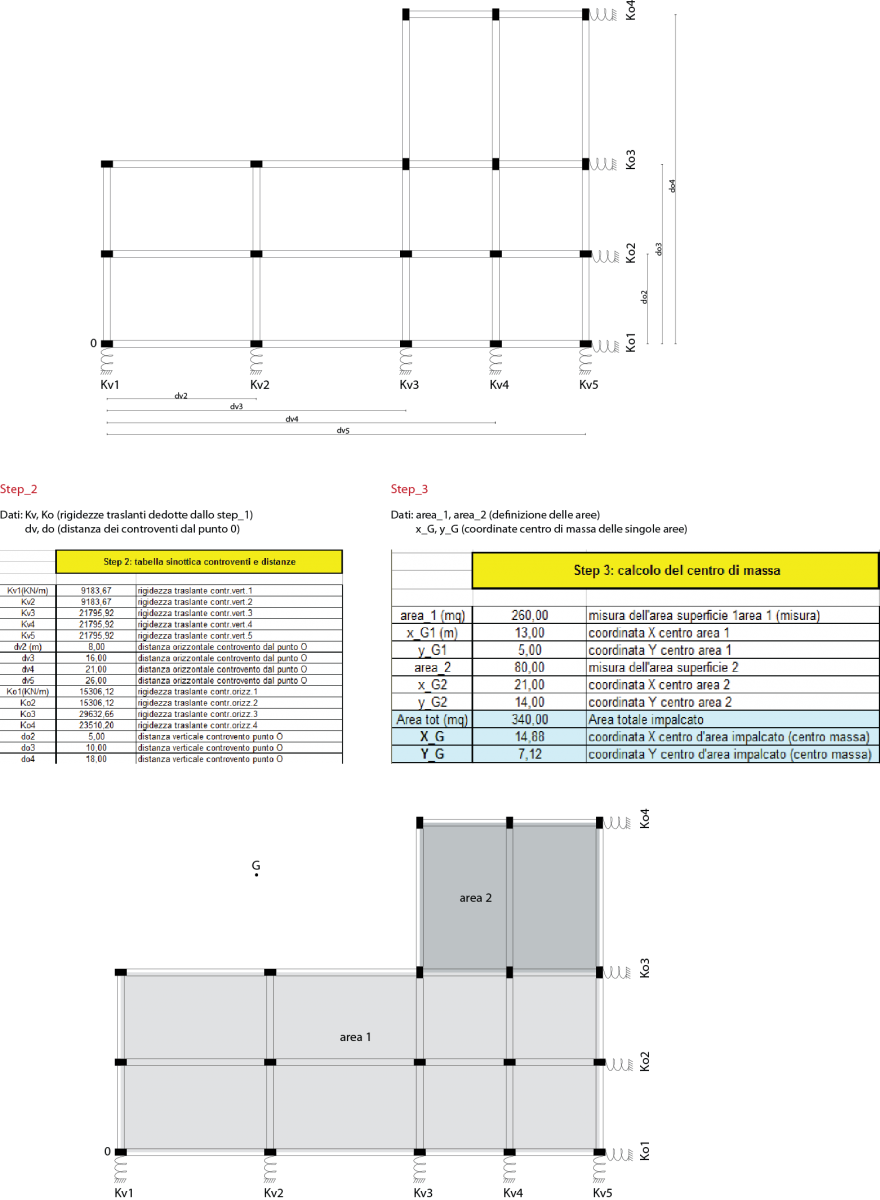
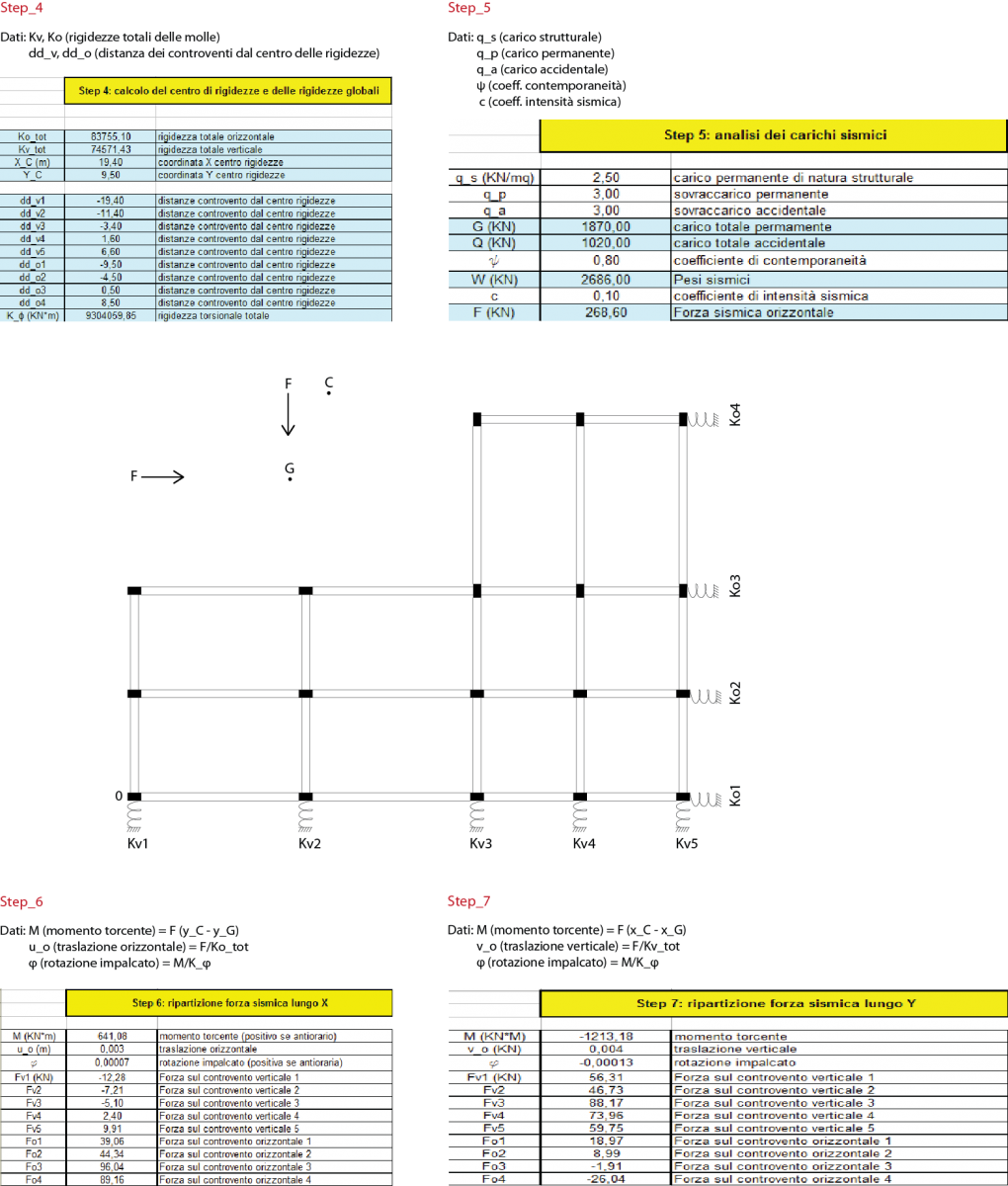
Es6_Controventi e ripartizione forze sismiche

Inviato da giulia.sabbatini il Lun, 13/05/2013 - 15:46

 

Controventi
 
Un impalcato, composto da tutti gli elementi orizzontali del telaio, è rigido nel suo piano e flessibile fuori dal piano.
Quindi le forze esterne agenti su di esso tendono a spostarlo e per contrastarle si utilizzano i controventi, elementi
elastici in grado di resistere all’azione delle forze orizzontali (sisma/vento).
 
 
Caso1
Consideriamo un impalcato con una forza F applicata. I controventi possiamo assimilarli a due molle (vincoli cedevoli)
entrambe aventi rigidezza pari a k.
 
                                                     
 
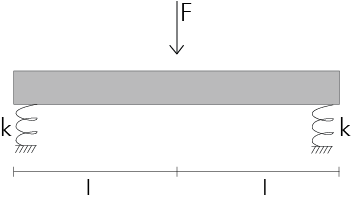
Essendo il sistema isostatico, posso facilmente conoscere le reazioni delle due molle, le quali generano anche una forza
uguale e opposta che provocherà un accorciamento (δsarà uguale perché le molle hanno la stessa rigidezza). 
 
                                                     

 

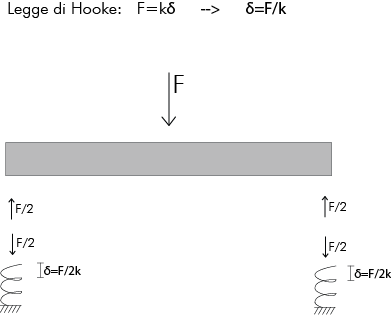
Quindi il corpo trasla di una quantitàche sarà pari a δ=F/2k
 
 
Caso 2
Ora considero lo stesso sistema isostatico precedente, ma con due molle aventi rigidezze diverse. Quindi la forza che
reagisce sul sistema provocherà due abbassamenti diversi a destra e a sinistra (il corpo ruota rigidamente).
                                                
                                                  
 
 
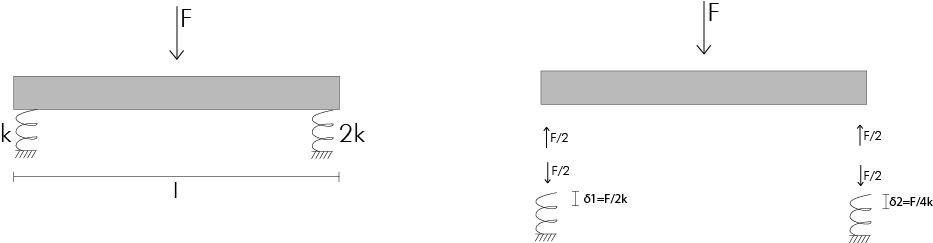
Ora ipotizzo che il sistema non ruoti, ma trasli di δ. In questo modo analizzo le reazioni vincolari e trovo il loro asse centrale.
 

 

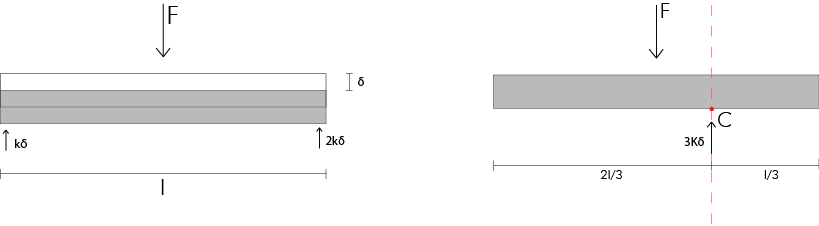
Dato che la forza F non coincide con l’asse delle rigidezze, il sistema tenderà a ruotare intorno al punto C.

 

 

Caso 3
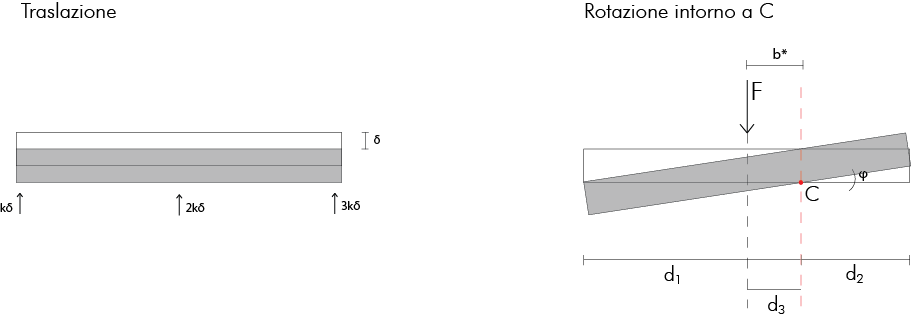
Nel caso di un sistema iperstatico, vedo i parametri di spostamento δ e φ come le mie incognite.
Per determinare il loro valore utilizzo le tre equazioni di equilibrio alla traslazione e alla rotazione del corpo rigido.
                                            

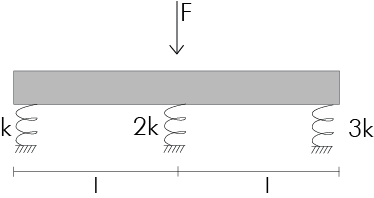
Cerco quindi il centro di queste forze:

 

 

 

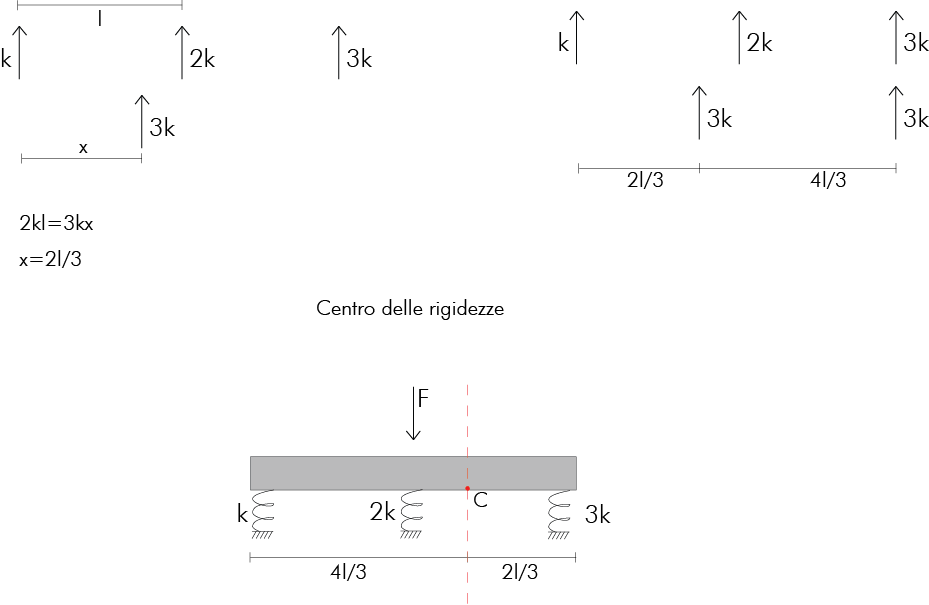
Importanti sono le distanze delle molle dal centro, perché è da questo che dipendo il loro
accorciamento o allungamento:
 
                                  
 

 

    - Equazioni di equilibrio alla traslazione:
 
     R1 = kδ + kφd1  
 
     R2 = 2kδ + 2kφd2                                        
 
     R3 = 3kδ - 3kφd3
 
     R1 + R2  + R3  = F                kδ + kφd1 + 2kδ + 2kφd2 + 3kδ - 3kφd3 = F
 
     6kδ + kφ ( d1 + 2d2 - 3d3 ) = F                           6kδ = F                           δ kδ = F                                                           
 
 
 
 
(Più grande è la forza, più grande sarà la rotazione dell’impalcato)
 
Dopo aver risolto rotazione e traslazione posso quindi trovare le reazioni iniziali R1, R2, R3
 
δ = F/ kδ                                                        
 
φ = Fb*/ kφ