Forze orizzontali e controventi

In questo blog si vuole determinare come e in che misura il seguente impalcato reagisce ad una forza orizzontale (sisma – vento), tramite l’azione dei controventi. Il soggetto in esame altro non è che il telaio (travi e pilastri allineati nello stesso piano) il quale non ha solo il compito di ripartire i carichi verticali ma anche quelli orizzontali.

Nello schema i controventi, in quanto hanno un comportamento elastico, vengono rappresentati come delle molle ognuna caratterizzata da una propria rigidezza, che può variare in funzione di alcuni parametri (ad esempio la sezione dei pilastri). Conoscendo il valore delle distanze delle molle dal punto di rotazione O (origine del sistema di coordinate), la dimensione dei pilastri(30cm x 40cm, h= 320 cm), il materiale utilizzato (calcestruzzo armato con modulo di Young E=210000 N/mm²), possiamo iniziare il calcolo dell’impalcato soggetto alla forza orizzontale “F”.

1-      Calcolo delle rigidezze traslanti dei controventi dell'edificio

In questo passaggio si vuole determinare quale è la forza, e quindi rigidezza, che i vari telai, presi in esame uno ad uno, oppongo alla traslazione lungo il loro asse. La rigidezza del telaio è il risultato della somma della rigidezza di ogni pilastro ad esso appartenete (proprio come nel modello shear-type) e vale:

Kᴛ = 12E Itot/h³

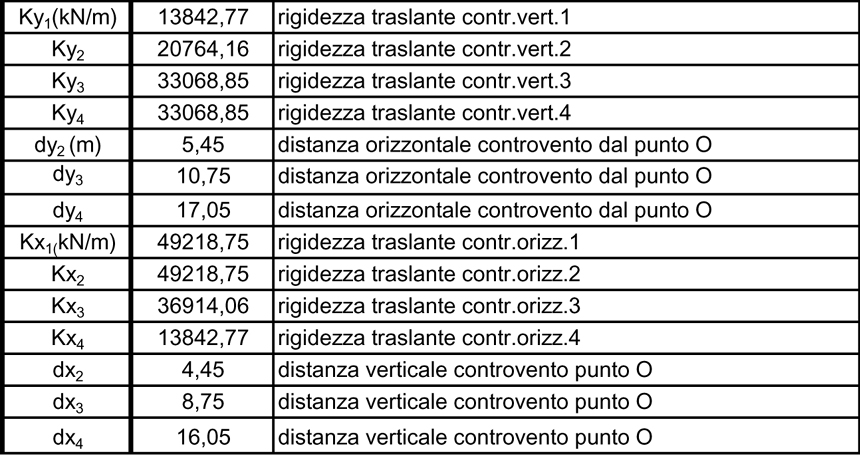
2-      Tabella sinottica controventi e distanze

Di seguito vengono riportate in tabella le rigidezze traslanti dei telai e la loro distanza dal punto di rotazione O

3-      Calcolo del centro di massa

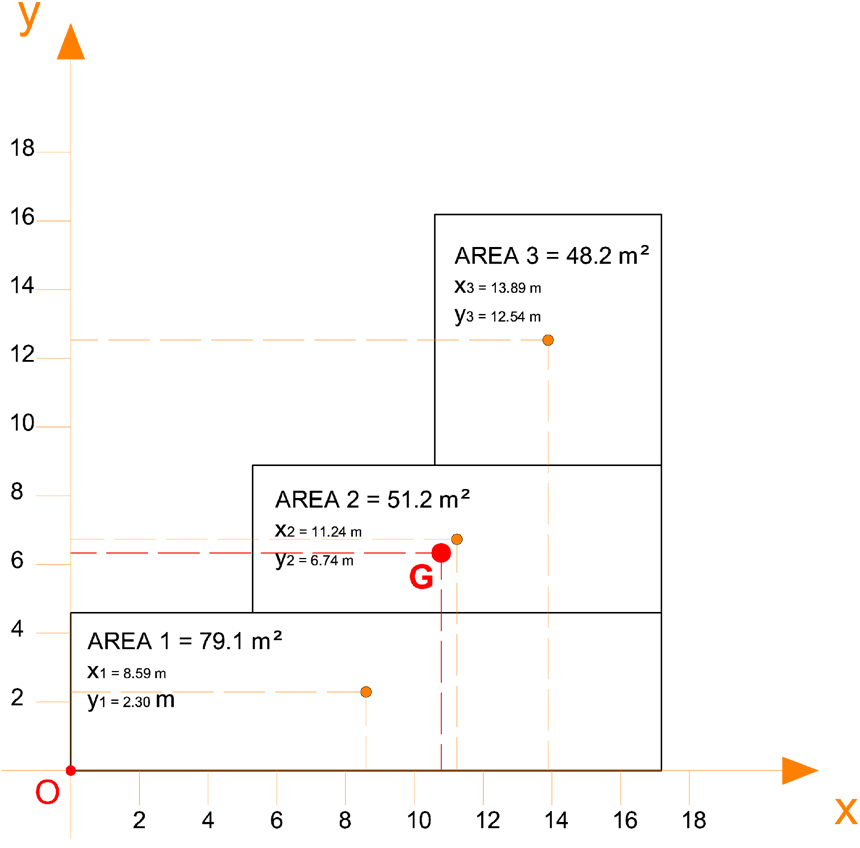
Siccome non è immediatamente riconoscibile il centro di massa, in quanto l’impalcato non è simmetrico, si procede semplificando l’impalcato stesso in forme semplici, rettangoli e/o quadrati, di cui vengono trovati facilmente i baricentri. Il centro di massa dell’intero impalcato non sarà altro che la somma delle coordinate, lungo x ed y, per le rispettive aree, diviso l’area totale dell’impalcato.

 Xg= (ΣXi * Ai) / Atot        con i che va da 1 a 3

 Yg= (ΣYi * Ai) / Atot

4-      Calcolo del centro di rigidezze e delle rigidezze globali

Il centro delle rigidezze è il centro del sistema di forze considerate, in cui viene applicata la risultante delle rigidezze traslanti dei controventi lungo l’asse x ed y. Ora non resta che ricavare le distanze dei controventi dal centro delle rigidezze in modo da trovare il valore della rigidezza torsionale (Kϕ) dell’impalcato che rappresenta la rigidezza complessiva a rotazione delle molle.

 Xc= (ΣKyi * dyi) / Kytot   con i che va da 1 a 4

 Yc= (ΣKxi * dxi) / Kxtot

 Kϕ= (ΣKi * di²)

5-      Analisi dei carichi sismici

A questo punto viene definita la forza sismica, applicata nel centro di massa, come il prodotto tra  la massa dell’impalcato e l’accelerazione del suolo dovuto al sisma.

F = m a

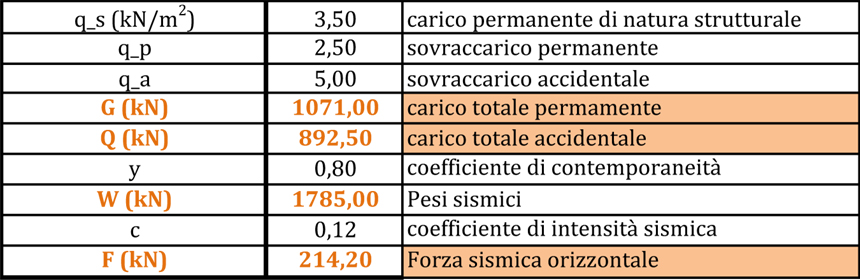
La massa dell’impalcato “W” è data dalla somma del carico totale permanente “G” e del carico totale accidentale “Q” per il coefficiente di intensità sismica “ψ” (da normativa), dove:

G =  (carico strutturale (qs ) + sovraccarico permanente (qp)) * l’area totale dell’impalcato (Ωtot)
Q = sovraccarico accidentale (qa) * l’area totale dell’impalcato (Ωtot)
L’accelerazione è data dalla normativa e dipende dal sito in esame. Prendiamo come riferimento la zona di Roma dove il valore della accelerazione è di 0,12.

6-      Ripartizione della forza sismica

Si arriva, infine a definire le incognite del problema e cioè la traslazione “u” lungo gli assi di riferimento e la rotazione “ϕ” dell impalcato per poi trovare il momento torcente  prodotto dalla forza sismica e ripartirla, cioè quantificare la forza che ogni controvento offre al sistema.

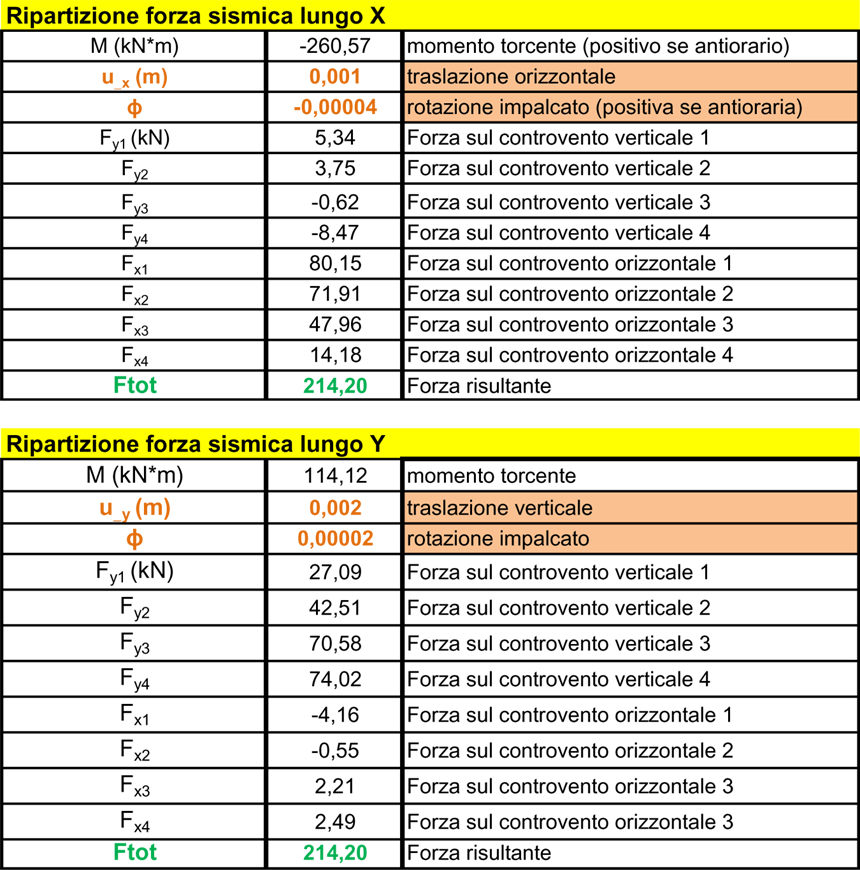
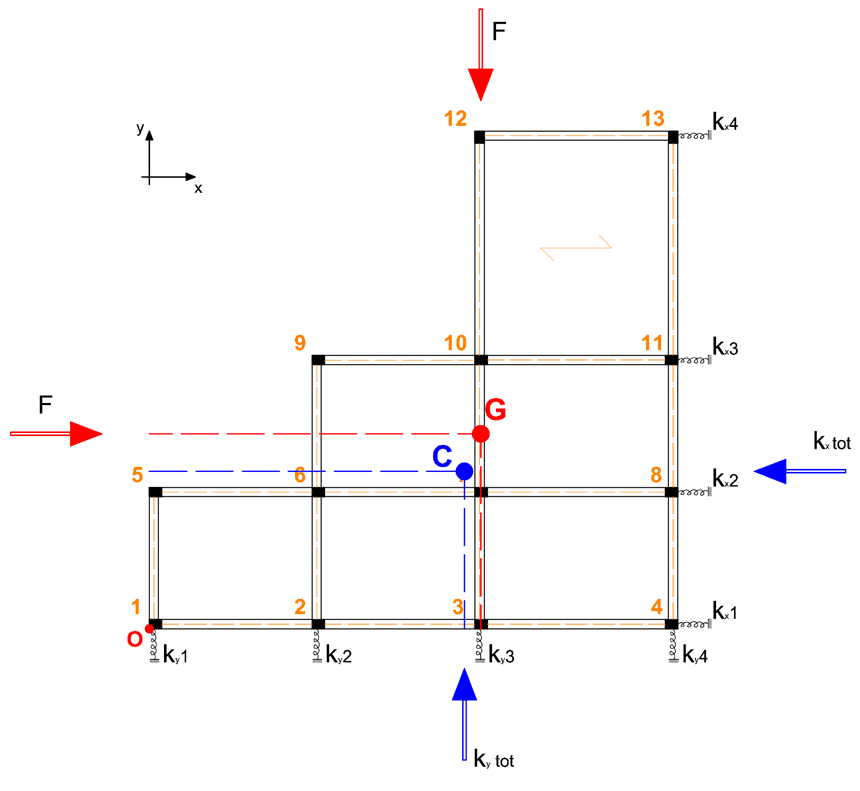
In generale l’impalcato esaminato ha un buon comportamento sismico in quanto centro delle masse e centro delle rigidezze sono molti vicini e ciò rende il momento torcente abbastanza contenuto, evitando che la rotazione sia eccessiva. Infine è interessante notare il comportamento di sistema dei controventi. I telai con un valore maggiore della rigidezza assorbono una quantità maggiore della forza sismica.

Chi più ha, più paga… mi sembra giusto!