Superare grandi luci è una sfida che mette, da secoli, in contrapposizione specialisti (architetti, ingegneri, etc) e natura: è l’idea che vuole liberarsi dalle regole fisiche-matematiche che governano il mondo in cui essa deve diventare materia. Il progettista oggi, nel tentativo di realizzare strutture di grande luce, ha a disposizione vari modelli. In questo blog si analizzerà la travatura reticolare che si basa su un' intuizione strutturale che fa dividere le grandi strutture inflesse in una serie di piccoli elementi tesi o compressi.
Di seguito si propone di risolvere una travatura reticolare utilizzando il metodo della sezione di Ritter.
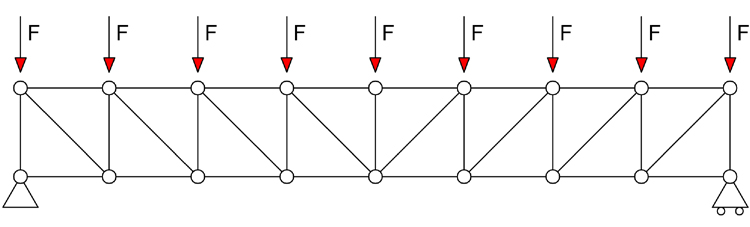
SCHEMA DI CALCOLO
Osservazioni:
- La trave reticolare è isostatica in quanto si comporta come un corpo rigido nel piano in cui i 3 gradi di libertà sono contrastati, esternamente, da un carrello ed una cerniera.
- Una trave reticolare per essere considerata tale deve essere composta da nodi e da aste sollecitate solo a sforzo normale dove, idealmente, le forze esterne agiscono direttamente sui nodi.
- La sezione di Ritter può interessare al massimo 3 aste della trave reticolare le quali non concorrono nello stesso nodo. La sezione, inoltre, divide la trave reticolare in due parti le quali vengono considerate come corpi rigidi.
Inizio numerando i nodi e trovando, poi, le reazioni vincolari.
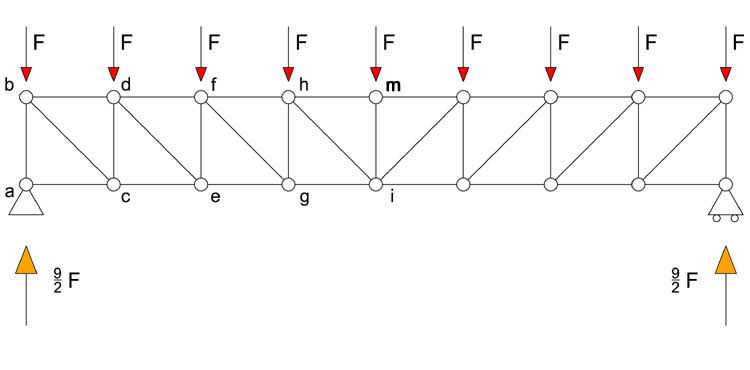
Trovo lo sforzo normale Nab utilizzando un’equazione di traslazione verticale. Per cui:
Nab + 9/2 F = 0 → Nab = -9/2 F (puntone)
Lo sforzo normale, ipotizzato di trazione, è invece di compressione e quindi l’asta è un puntone.
Dopo aver trovato le reazioni vincolari ed Nab effettuo il taglio virtuale della trave cioè la sezione di Ritter ed analizzo la parte su cui incidono meno forze per rendere i calcoli più veloci. La sezione determina tre incognite e si hanno a disposizione tre equazioni per cui il problema ammette soluzione. In particolare si utilizzeranno equazioni di equilibrio a rotazione e traslazione. In una prima ipotesi le forze vengono considerate sempre di trazione.
Sezione 1
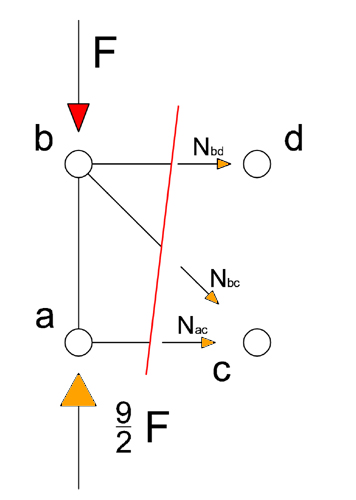
Equilibrio a rotazione intorno al polo “c”
-Nbdl + F l – 9/2 F l = 0 → Nbd = - 7 rad2 /2 F (puntone)
Equilibrio a rotazione intorno al polo “b”
Nacl = 0 → Nac = 0 (asta scarica)
Per trovare Nbc scompongo la forza nelle sue due componenti (verticale ed orizzontale) ed impongo l’equilibrio alla traslazione verticale. Per cui:
- 
rad2 /2 Nbc– F + 9/2 F = 0 → Nbc = 7
/2 F(tirante)
Noto il valore delle forze delle aste in esame effettuerò altre sezioni sulle aste il cui valore dello sforzo normale è sconosciuto.
Sezione 2
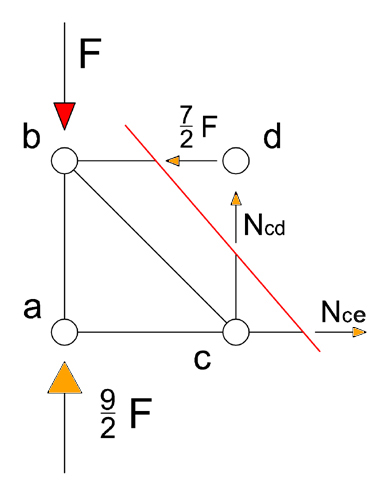
Equilibrio a rotazione intorno al polo “d”
Nce l + F l – 9/2 F l = 0 → Nce = 7/2 F (tirante)
Equazione di equilibrio alla traslazione verticale
Ncd+ 9/2 F – F = 0 → Ncd = - 7/2 F (puntone)
Sezione 3
Equilibrio a rotazione intorno al polo “e”
- Ndfl + 3F l – 9/2 F (2 l) = 0 → Ndf = -6F (puntone)
Equazione di equilibrio alla traslazione orizzontale
(considero la componente orizzontale di Nde)
rad2 /2 Nde – 6F + 7/2 F = 0 → Nde = 5 rad2 /2 F (tirante)
Sezione 4
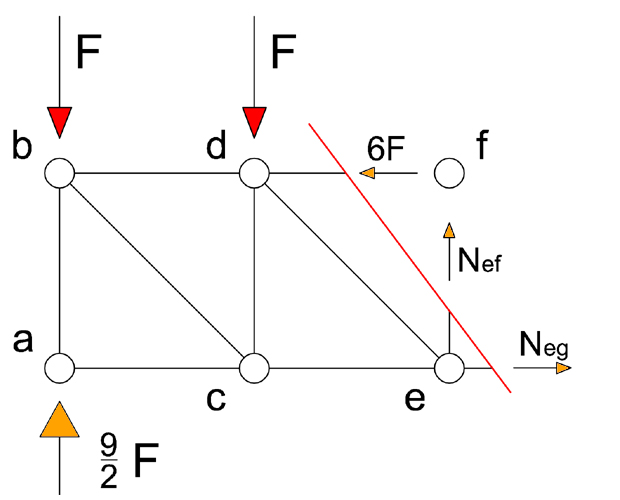
Equilibrio a rotazione intorno al polo “ f ”
Neg l + 3F l – 9F l = 0 → Neg= 6F (tirante)
Equilibrio alla traslazione verticale
Nef– 2F + 9/2 F = 0 → Nef = -5/2 F (puntone)
Sezione 5
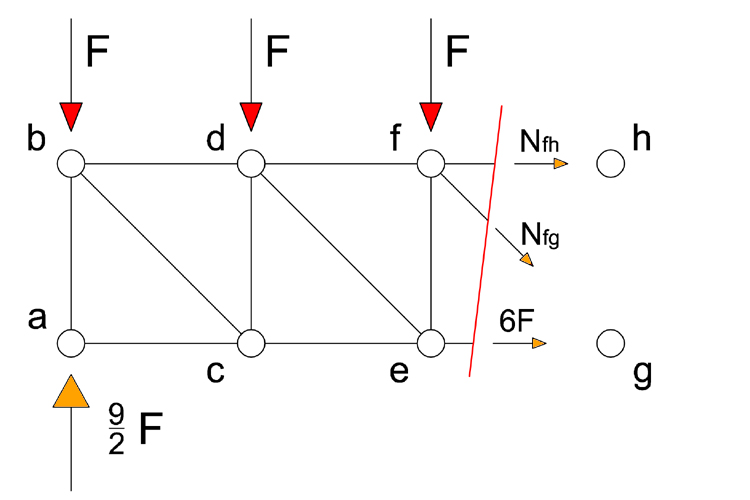
Equilibrio a rotazione intorno al polo “ g ”
- Nfhl + 6F l – 9/2F 3l = 0 → Nfh = -15/2 F (puntone)
Equilibrio alla traslazione orizzontale
rad2 /2 Nfg– 15/2F + 6F=0 → Nfg = 3 rad 2 /2 F (tirante)
Sezione 6
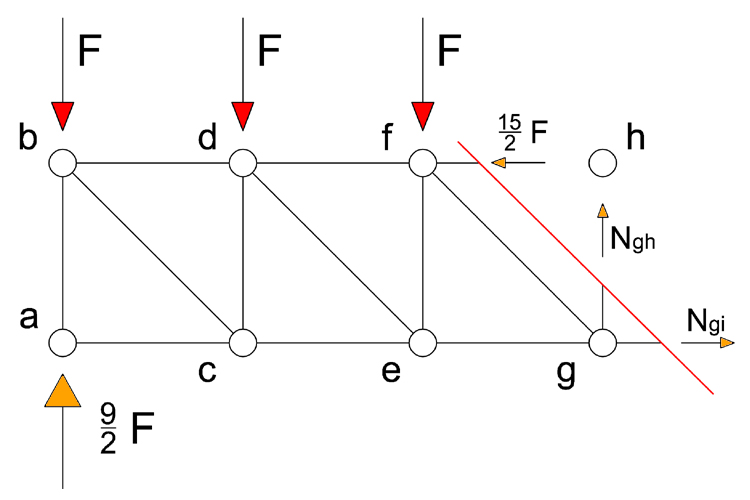
Equilibrio a rotazione intorno al polo “ h ”
Ngi l + 6F l – 9/2F (3l) = 0 → Ngi = 15/2 F (tirante)
Equilibrio alla traslazione verticale
Ngh– 3F + 9/2F=0 → Ngh = - 3/2 F (puntone)
Sezione 7
Equilibrio a rotazione in “ i ”
- Nhm l + 10F l – 18F l = 0 → Nhm = -8 F (puntone)
Equilibrio traslazione orizzontale
rad2 /2 Nhi - 8F + 15/2 F = 0 → Nhi = rad2 /2 F (tirante)
Il valore dello sforzo normale Nmi è pari alla forza esterna agente sul nodo “m”. Per cui:
Nmi = - F (puntone)
La struttura è simmetrica e simmetricamente caricata per cui i valori dello sforzo normale delle aste trovati valgono pure per la restante parte della trave reticolare. Di seguito vengono proposti tutti gli sforzi delle aste.
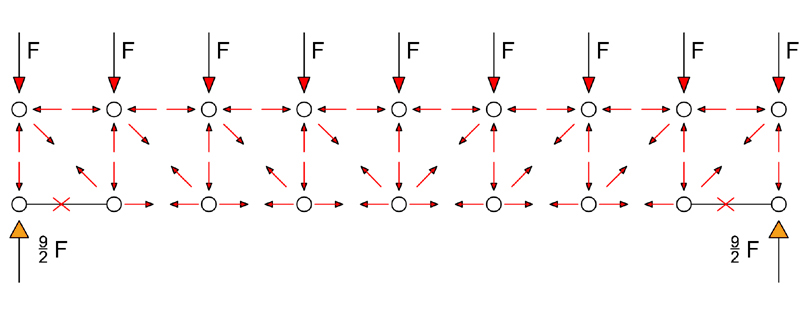
DEFORMATA
DIAGRAMMA SFORZO NORMALE
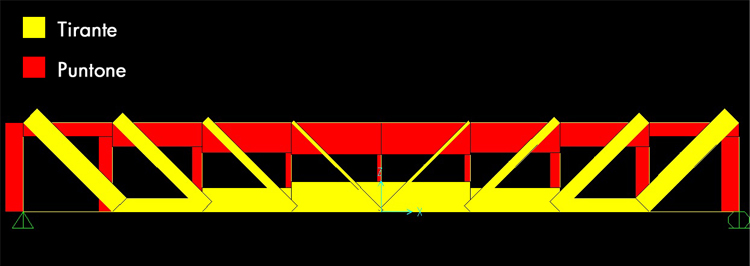
Dal diagramma si può notare come le aste del corrente superiore e le aste verticali siano compresse mentre quelle del corrente inferiore e quelle oblique siano tese.
TRAVATURA RETICOLARE 3D
SAP 2000
In questo esercizio si risolverà una trave reticolare nello spazio tramite l’utilizzo del programma SAP 2000.
La prima operazione è quella di importare lo schema di trave, precedentemente disegnata in AutoCAD:
1. File – Import – AutoCAD.dxf file
Fatto questo nell’analisi decido di trascurare il peso proprio della trave in modo da non avere né taglio né momento. Per cui:
2. Define – Load patterns – Self weight multiplier = 0
Successivamente bisogna assegnare i vincoli. Siccome ci troviamo nello spazio la travatura reticolare presenta 6 gradi di libertà, per cui per renderla isostatica utilizzo 3 cerniere esterne stando attento che questi non siano allineati altrimenti renderebbero la struttura labile.
Una volta selezionati i punti in cui inserire i vincoli si procede in questo modo:
3. Assign – Joint – Restraints – cerniera
Assegnati i vincoli esterni bisogna assegnare il rilascio ai nodi della trave reticolare cioè si impone che i nodi non reagiscano a momento.
4. Assign – Frame – Releases – Moment (3,3) start = 0 , end = 0
A questo punto è possibile definire il carico che, come nel caso della trave reticolare 2d, deve agire sui nodi. Per cui si selezionano i nodi superiori e procedo assegnando una forza concentrata di 20 Kn per ogni nodo:
5. Assign – Joint loads – Forces – lungo asse z – 20 kN
Non resta, infine, che definire materiale e sezione delle aste. Si ipotizzerà una struttura con aste in acciaio con un modulo di Young E = 210000 N/mm² e con una sezione circolare cava con un diametro esterno di 10 cm ed uno spessore di 0,05 cm. Per cui:
6. Define – Materials – Add new material – Steel
7. Define – Section properties – Frame sections – New properties – Pipe
Ultimo passaggio consiste nell’avviare l’analisi ed esportare le tabelle con i risultati.
8. F5 per avviare l’analisi
DEFORMATA
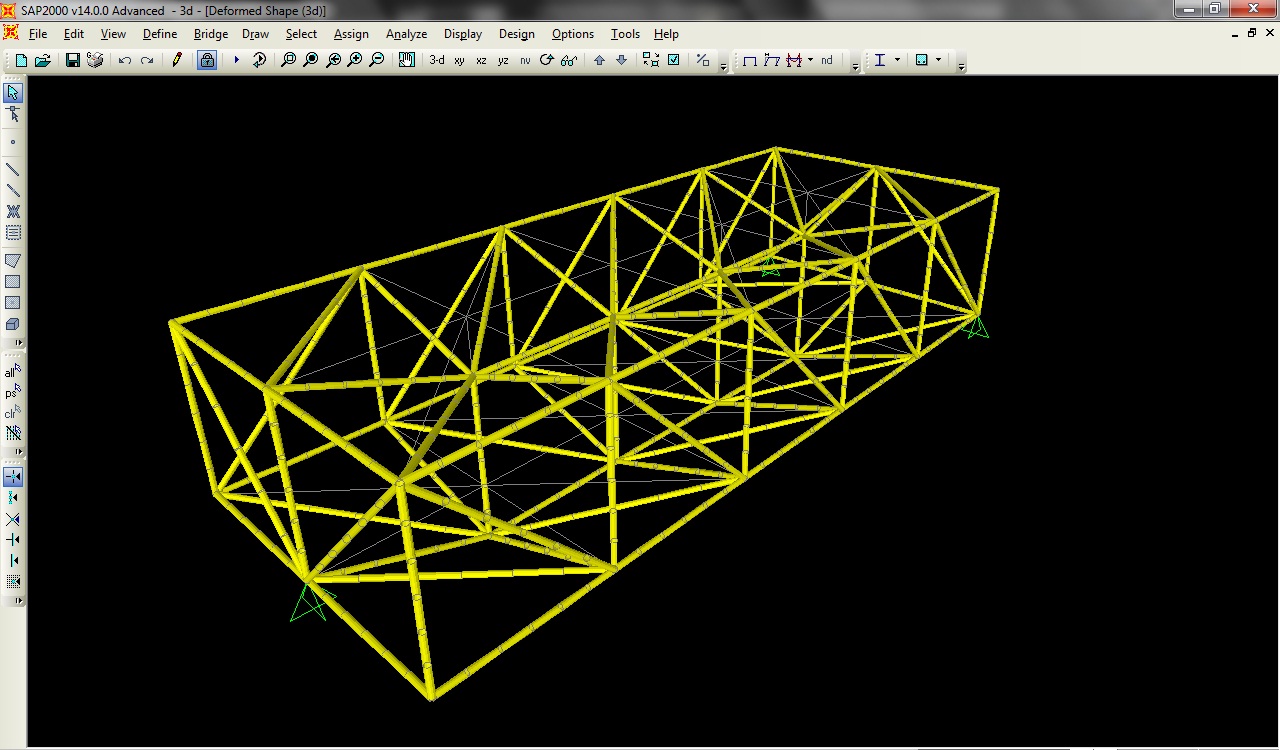
DIAGRAMMA SFROZO NORMALE
Il fatto che non tutte le aste concorrano a contrastare le forze esterne e che ci siano alcune particolarmente sollecitate fa pensare che queste siano state disposte in un modo errato. Probabilmente rendendo la travatura simmetrica nello spazio questa avrebbe un comportamento migliore.
9. Display – Show tables – Analysis results – Export all tables to excel
Al blog viene allegato un file excel contenente delle tabelle che mostrano le tensioni che si generano in ogni singola asta.
Totale 622,9 Kg/m² ≈ 6,3 kN/m²
Commenti recenti