Vierendeel, rigidezze e spostamenti

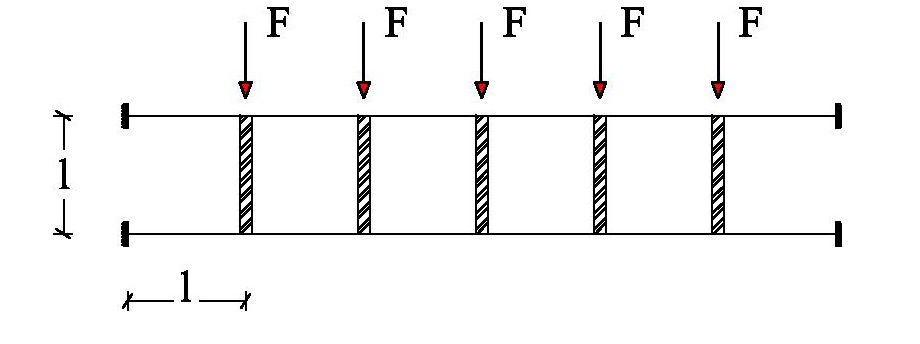
In questo blog si continua a trattare il problema iperstatico, stavolta risolto col metodo delle rigidezze. In particolare viene calcolata una trave vierendeel in cui i pilastri sono infinitamente rigidi e i traversi deformabili.

SCHEMA DI CALCOLO

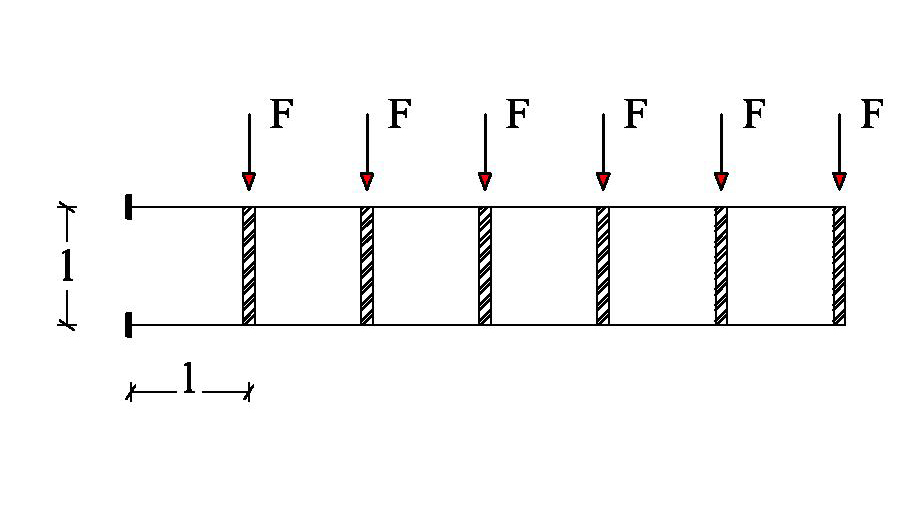
Per effetto delle forze esterne, i pilastri traslano, senza deformarsi, di una quantità δ.

DEFORMATA

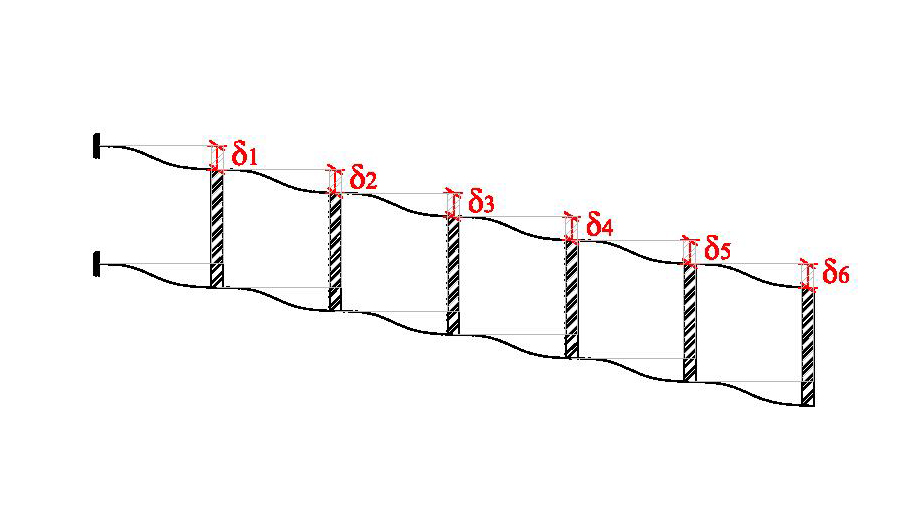
La trave in esame ha lo stesso comportamento di un telaio “shear-type” in cui conoscendo il valore degli spostamenti  δ è possibile determinare il valore delle caratteristiche di sollecitazione e delle rigidezze dei traversi. Riferendoci, infatti, ad una trave doppiamente incastrata soggetta ad un cedimento vincolare si hanno i seguenti valori notevoli del momento e del taglio nei vincoli.

SCHEMA NOTEVOLE

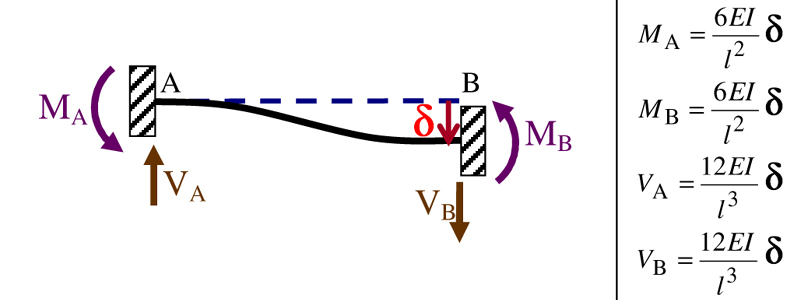
Il problema iperstatico verrà, quindi, risolto scrivendo per ogni incognita (spostamento) un’equazione alla traslazione verticale.

RISOLUZIONE: 6 equazioni alla traslazione verticale per 6 incognite (δ6, δ5,δ4,δ3,δ2,δ1)

1.      F = 2T  →  F = 24 EI/l³ δ6  →  δ6= Fl³/24 EI

T = 12 EI/l³ δ6  

T = 12 EI/l³ * (Fl³/24 EI) = F/2

M = 6 EI/l²  δ6 = Fl/4

2.      F + F/2 + F/2= 2T  →  2F = 24 EI/l³ δ5  →  δ5= Fl³/12 EI

T = 12 EI/l³ δ5

T = 12 EI/l³ * (Fl³/12 EI) = F

M = 6 EI/l²  δ5 = Fl/2

3.      F + F + F= 2T  →  3F = 24 EI/l³ δ4  →  δ4= Fl³/8 EI

T = 12 EI/l³ δ4

T = 12 EI/l³ * (Fl³/8 EI) = 3/2F

M = 6 EI/l²  δ4= 3/4 Fl

4.      F + 3/2F + 3/2F= 2T  →  4F = 24 EI/l³ δ3  →  δ3= Fl³/6 EI

T = 12 EI/l³ δ3

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²  δ3=  Fl

5.      F + 2F + 2F= 2T  →  5F = 24 EI/l³ δ2  →  δ2= 5 Fl³/ 24EI

T = 12 EI/l³ δ2

T = 12 EI/l³ * (5 Fl³/24 EI) = 5/2F

M = 6 EI/l²  δ2=  5/4Fl

6.      F + 5/2F + 5/2F= 2T  →  6F = 24 EI/l³ δ1  →  δ1= Fl³/4 EI

T = 12 EI/l³ δ1

T = 12 EI/l³ * (Fl³/4 EI) = 3F

M = 6 EI/l²  δ1=  3/2 Fl

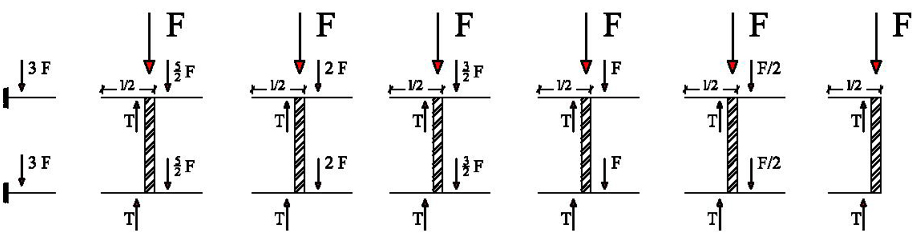
Determinato Taglio, Momento e rigidezze dei traversi, trovo momento e taglio anche nei pilastri.

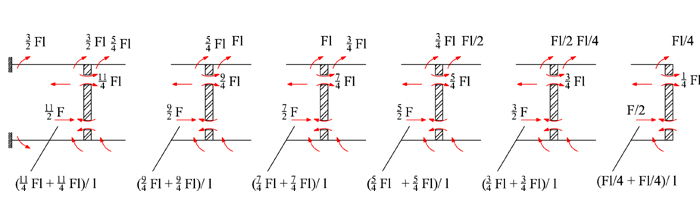
DIAGRAMMA TAGLIO E MOMENTO

Allo stesso modo di prima, siamo in grado di risolvere lo stesso tipo di trave, stavolta doppiamente incastrata.

SCHEMA DI CALCOLO

Bisogna notare che la trave è simmetrica e simmetricamente caricata per cui basta studiarne la metà ed in corrispondenza della simmetria bisogna considerare la forza di valore pari a F/2

DEFORMATA

RISOLUZIONE:3 equazione alla traslazione verticale per 3incognite (δ3,δ2,δ1)

1.      F/2 = 2T  →  F = 48 EI/l³ δ3  →  δ3= Fl³/48 EI

T = 12 EI/l³ δ3  

T = 12 EI/l³ * (Fl³/48 EI) = F/4

M = 6 EI/l²  δ3= Fl/8

2.      F + F/4 + F/4 = 2T  → 3/2 F = 24 EI/l³ δ2  →  δ2= Fl³/16 EI

T = 12 EI/l³ δ2  

T = 12 EI/l³ * (Fl³/16 EI) = 3/4 F

M = 6 EI/l²  δ2= 3/8 Fl

3.      F + 3/4F + 3/4F = 2T  → 5/2 F = 24 EI/l³ δ1  →  δ1= 5 Fl³/48 EI

T = 12 EI/l³ δ1  

T = 12 EI/l³ * (5 Fl³/48EI) = 5/4 F

M = 6 EI/l²  δ1= 5/8 Fl

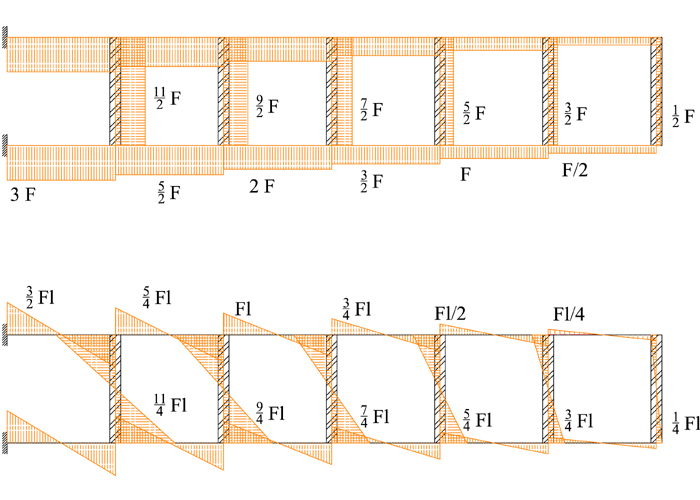
TRAVERSI

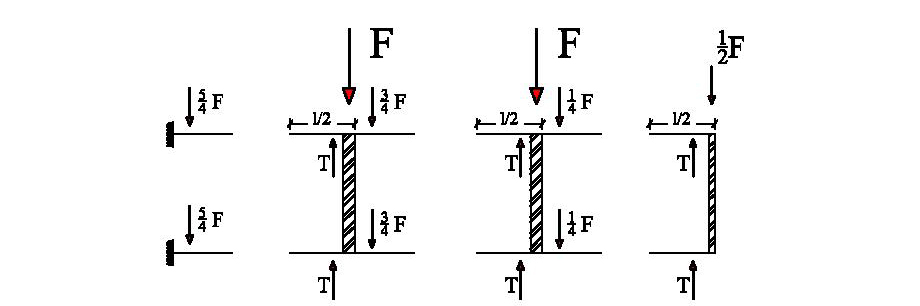
PILASTRI

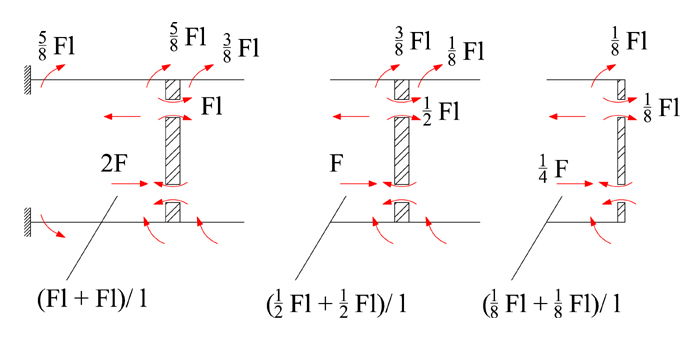
DIAGRAMMI TAGLIO E MOMENTO

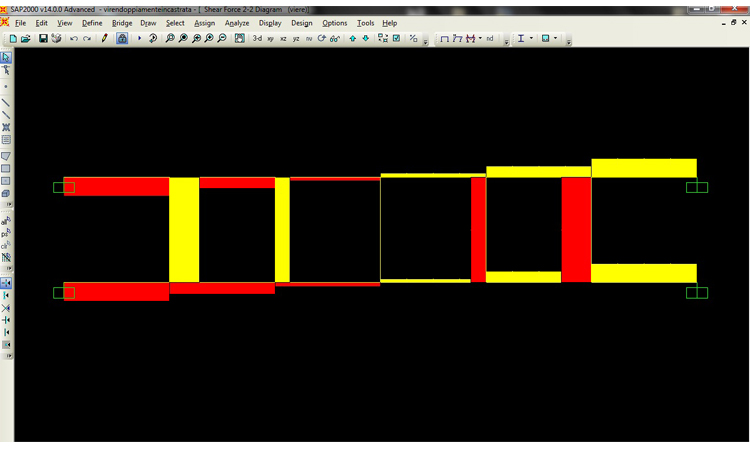
VERIFICA IN SAP2000

Questione cruciale consiste nel far capire al programma che i pilastri sono infinitamenti rigidi. Per fare ciò, o si dà un valore elevato al modulo di Young al materiale con cui è fatto il pilastro, o si aumenta a dismisura la sezione del pilastro stesso. In particolore ho dato un valore altissimo al modulo di Young del materiale che costituisce il pilastro a cui tra l'altro ho assegnato una sezione di 1m x 1m, mentre alla trave è stata assegnata una sezione molto piccola.

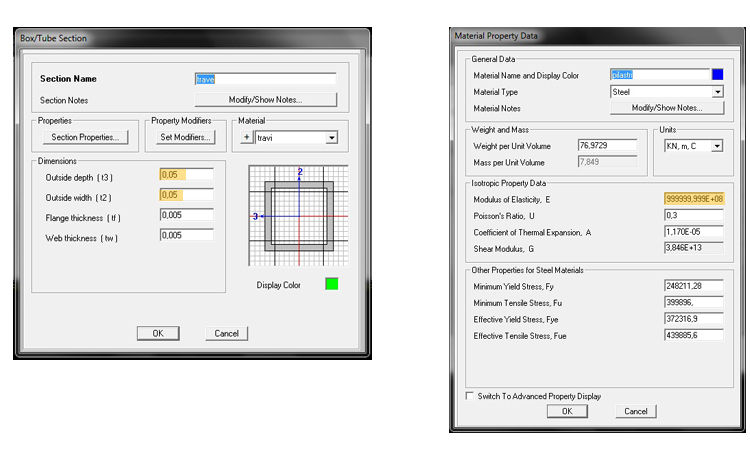
Di seguito vengono proposti gli schemi finali:

Esercizio 1

DEFORMATA

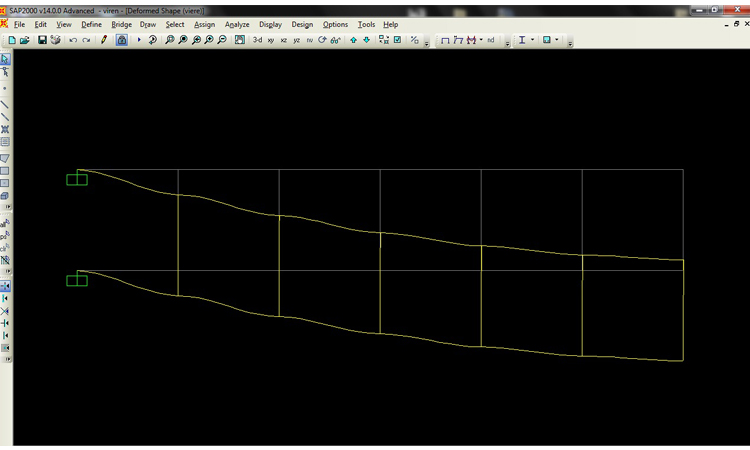
DIAGRAMMA MOMENTO

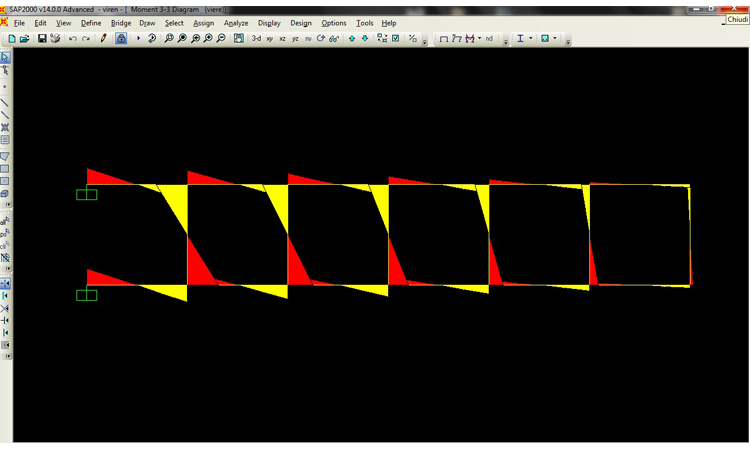
DIAGRAMMA TAGLIO

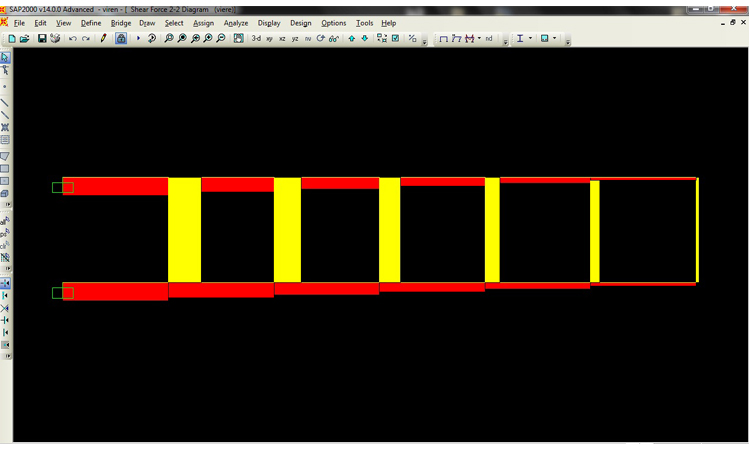
Esercizio 2

DEFORMATA

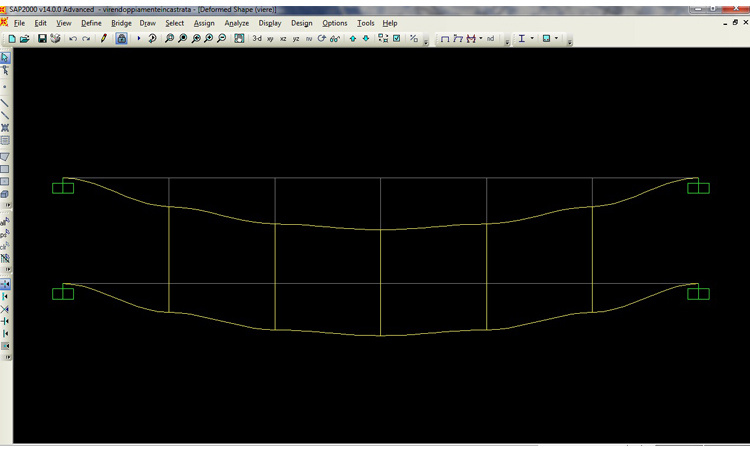
DIAGRAMMA MOMENTO

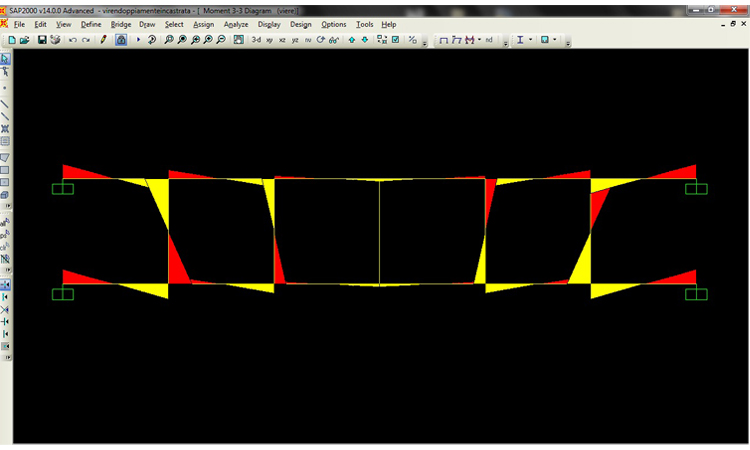
DIAGRAMMA TAGLIO