Linea elastica

Comunemente, in meccanica, quando ci si riferisce ad una struttura in cui il numero delle equazioni di equilibrio fornite dalla statica risulta essere minore del numero delle incognite, si parla di “problema iperstatico”. In realtà il problema riguarda solo il calcolo della struttura, la quale sicuramente ha un comportamento migliore se iperstatica. Non per altro le costruzioni che ci circondano, nella maggior parte dei casi, hanno strutture iperstatiche (mi vengono subito in mente telai in c.a., ad esempio).

In questo esercizio si vuole risolvere una trave iperstatica soggetta ad un carico q₂ con l’obiettivo di conoscere in quale sezione si ha l’abbassamento massimo e quanto vale quest’ultimo.

La risoluzione avviene attraverso l’utilizzo dell’equazione della linea elastica, la quale “risolve” il problema iperstatico tenendo conto delle caratteristiche meccaniche del materiale, le caratteristiche geometriche della sezione (area, inerzia), tutte legate alla deformabilità della trave.

Il problema iperstatico presenta 8 incognite (forze interne, spostamenti, deformazioni). Considerando le incognite che dipendono solo dallo spostamento possiamo combinare le varie equazioni che derivano dal modello di trave di Bernoulli, ottenendo:

EQUAZIONI DI BILANCIO

dT/ds + q₂= 0     (a)

dM/ds + T               →     T= - dM/ds       (b)

Sostituendo (b) in (a) si ottiene:

(d/ds) (- dM/ds) + q₂= 0       →      -d²M/ds² + q₂= 0     (c)

EQUAZIONI DI CONGRUENZA

χ = dφ/ds = (d/ds) (dv/ds) = d²v/ds²

LEGAME COSTITUTIVO

M = EI χ = EI (d²v/ds²)                  (d)

Sostituendo (d) in (c) si ottiene:

(d²/ds²) EI (d²v/ds²) =       →       d⁴v/ds⁴ = q₂/EI

Si è ottenuto un’equazione differenziale lineare del quarto ordine della linea elastica che mette in relazione i carichi agenti su di una trave (noto) con gli spostamenti da essi prodotti (incognite del problema). La funzione incognita dell’abbassamento v(s) si ottiene integrando 4 volte:

d³v/ds³ = (q₂/EI) s + C₁               →   T                Taglio

d²v/ds² = (q₂/EI) s²/2 + C₁s + C₂          →  M            Momento

dv/ds = (q₂/EI) s³/6 + C₁ s²/2   + C₂ s + C₃    →  φ             Rotazione

v (s) = (q₂/EI) s⁴/24 + C₁ s³/6 + C₂s²/2 + C₃ s + C₄   →             Spostamento

SCHEMA DI CALCOLO

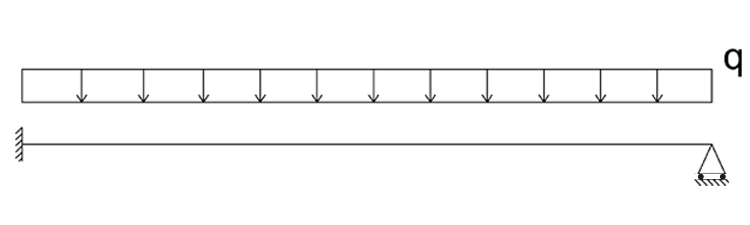
La trave in esame presenta un incastro al primo estremo ed un carrello al secondo estremo, per cui le condizioni al bordo sono:

V(0) = 0    →   C₄=0

φ(0) = 0    →   C₃=0

V(l) = 0

(- q₂/EI) l⁴/24 + C₁ l³/6 + C₂l²/2 = 0              →  C₂= (q₂/EI) l²/12 - C₁ l/3

M(l) = 0

(- q₂/EI) l²/2 + C₁ l +(q₂/EI) l²/12 - C₁ l/3 = 0      →  C₁= 5q₂l/8EI

Sostituisco il valore trovato della costante C₁ nell’equazione con incognita la costante C₂:

C₂= (q₂/EI) l²/12 – (5q₂l/8EI) l/3                    →  C₂= -q₂l²/ 8EI

Trovate le 4 costanti di integrazione posso conoscere in quale sezione della trave si ha l’abbassamento massimo e quanto vale. Per conoscere la sezione faccio una considerazione e cioè in corrispondenza della rotazione nulla si trova l’abbassamento massimo in quanto v’(s) = φ.

Per cui pongo l’equazione della rotazione prima definita uguale a zero e sostituisco alle costanti di integrazione i valori trovati ottenendo:

φ = dv/ds = (- q₂/EI) s³/6 + (5q₂l/8EI) s²/2 – (q₂l²/8EI) s

L’equazione di terzo grado in s mi darà 3 sezioni della trave in cui la rotazione sarà nulla. Mi aspetto di trovare una sezione in corrispondenza dell’incastro, una sezione in cui trovo vmax  e un punto esterno alla trave.

Trovata la sezione “s” in cui c’è il massimo abbassamento, trovo quanto questo vale. Conoscendo lo spostamento v(s), incognita del problema iperstatico, riesco ad ottenere le reazioni vincolari e tutte le caratteristiche di sollecitazione sezione per sezione.

In allegato c’è la risoluzione analitica dell’esercizio in esame.

A questo punto verifico i risultati ottenuti, utilizzando il programma di calcolo SAP2000.

Disegno la struttura, spezzandola già in corrispondenza della sezione in cui mi aspetto di trovare il massimo abbassamento in modo tale da leggerne facilmente il valore. Applico i vincoli all’estremità e carico la struttura con un carico q₂= 10 kN/m. Definisco, infine, la sezione ed avvio l’analisi.

DEFORMATA

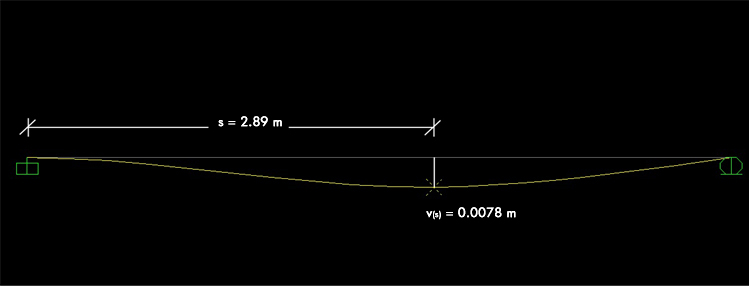
DIAGRAMMA MOMENTO

DIAGRAMMA TAGLIO

I valori di taglio e momento così come l’abbassamento sono pressoché uguali. Le piccole differenze sono dovute probabilmente alle approssimazioni che ho utilizzato durante il calcolo.