Problema iperstatico - Trave continua

Dopo la linea elastica, si utilizza un altro strumento per risolvere il problema iperstatico. In particolare si vuole risolvere una trave continua su più appoggi, 3 volte iperstatica, attraverso il metodo delle forze.

 Lo schema di calcolo è il seguente:

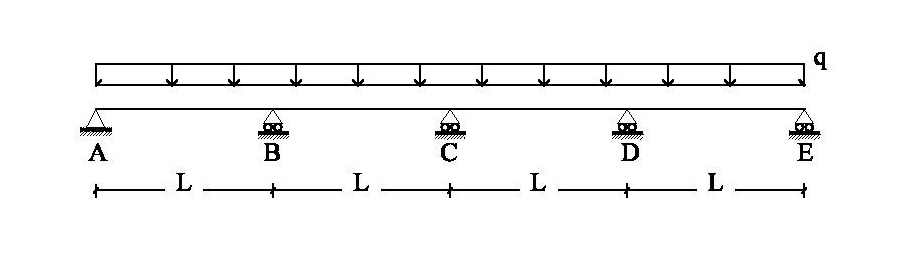
I valori delle rotazioni dovute sia alla forza X  che al carico q non saranno calcolate, ma saranno ricavate dai seguenti schemi notevoli:

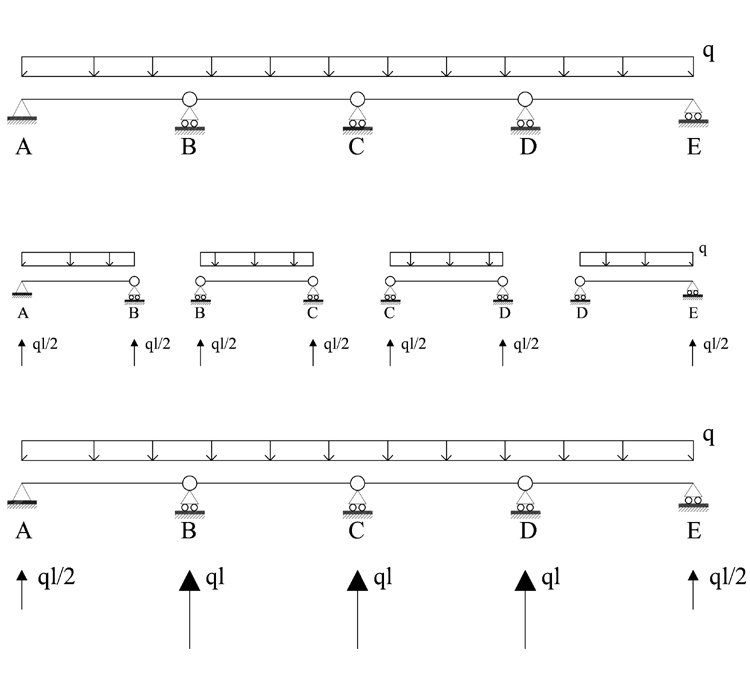
1.      SCHEMA ISOSTATICO EQUIVALENTE, nel quale, in corrispondenza degli appoggi rappresentati dai carrelli, rompo la continuità della trave ( abbassando i gradi di vincoli da tre a due).

2.      EQUAZIONI DI VINCOLO E EQUAZIONI DI COMPATIBILITA’CINEMATICA
Impongo che in corrispondenza degli appoggi la rotazione relativa sia uguale a zero in modo che venga ripristinata l’azione del vincolo cinematico soppresso.

Equazioni di vincolo

·         ∆φB = 0

·         ∆φC = 0

·         ∆φD = 0

Equazioni di compatibilità cinematica

·         ∆φB = φBs – φBd = 0

φBs = φBs (q) + φBs (X1) =  ql³/24EI – X1L / 3EI

φBd = φBd (q) + φBd (X1) + φBd (X2) = - ql³/24EI + X1L/3EI + X2L/6EI

ql³/24EI – X1L / 3EI + ql³/24EI - X1L/3EI - X2L/6EI = 0       →       X₁= - ql²/8 - X₂/4

·       ∆φD = ∆φC = φCs – φCd = 0

φCs = φCs (q) + φCs (X1) + φCs (X2) =  ql³/24EI – X1L / 6EI – X2L / 3EI

φCd = φCd (q) + φCd (X1) + φCd (X2) = - ql³/24EI + X1L/6EI + X2L/3EI

ql³/24EI – X1L / 6EI – X2L / 3EI + ql³/24EI - X1L/6EI - X2L/3EI = 0 → X₂= ql²/8 - x₁/2

3.      RISOLUZIONE DEL SISTEMA DI EQUAZIONI

X₁= - ql²/8 - X₂/4

X₂= ql²/8 - x₁/2

X1= 3/28 ql²

X2= ql²/14

4.      SOVRAPPOSIZIONE EGLI EFFETTI

Trovato il valore delle incognite iperstatiche, posso determinare il valore delle reazioni vincolari, utilizzando il principio della sovrapposizione degli effetti e tracciare infine i diagrammi di Taglio e Momento per la struttura in esame.

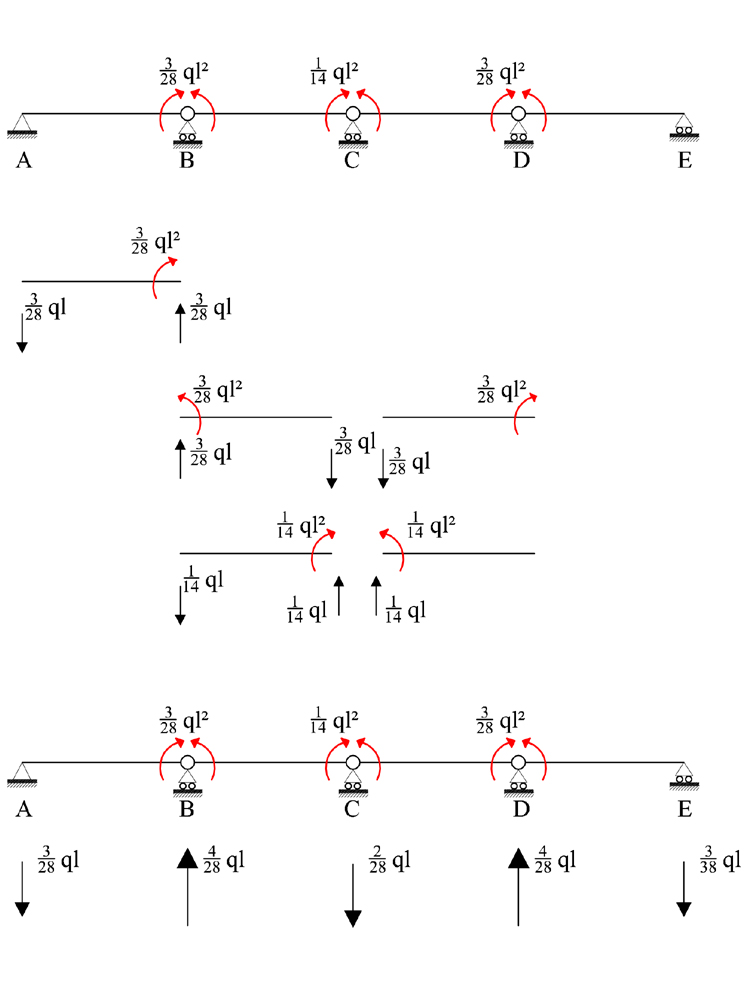
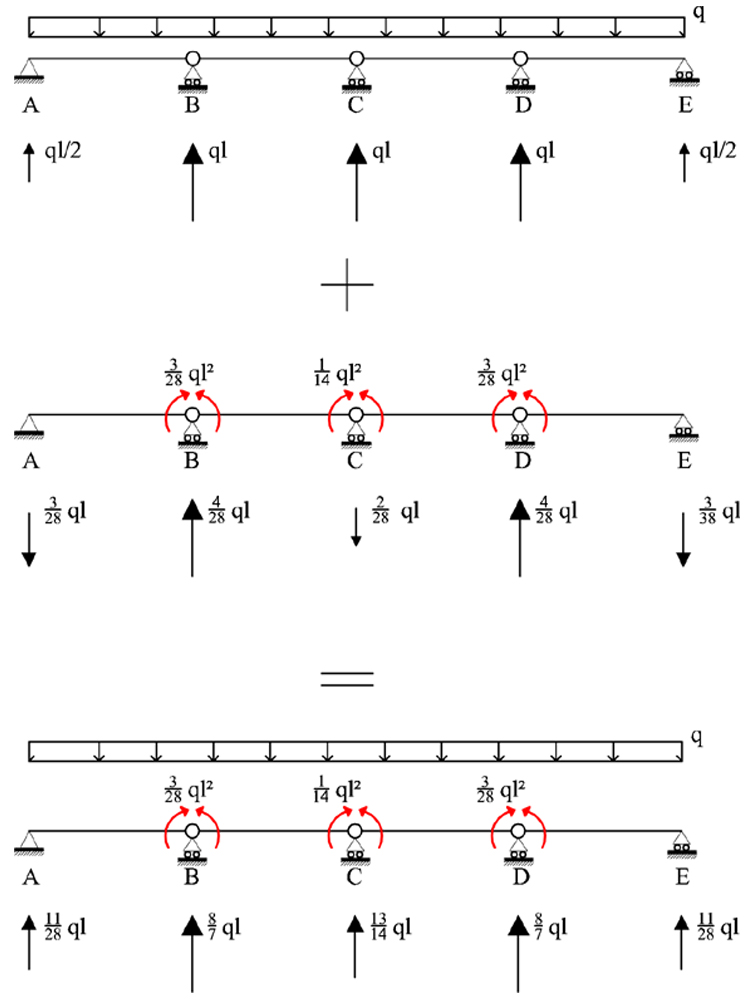
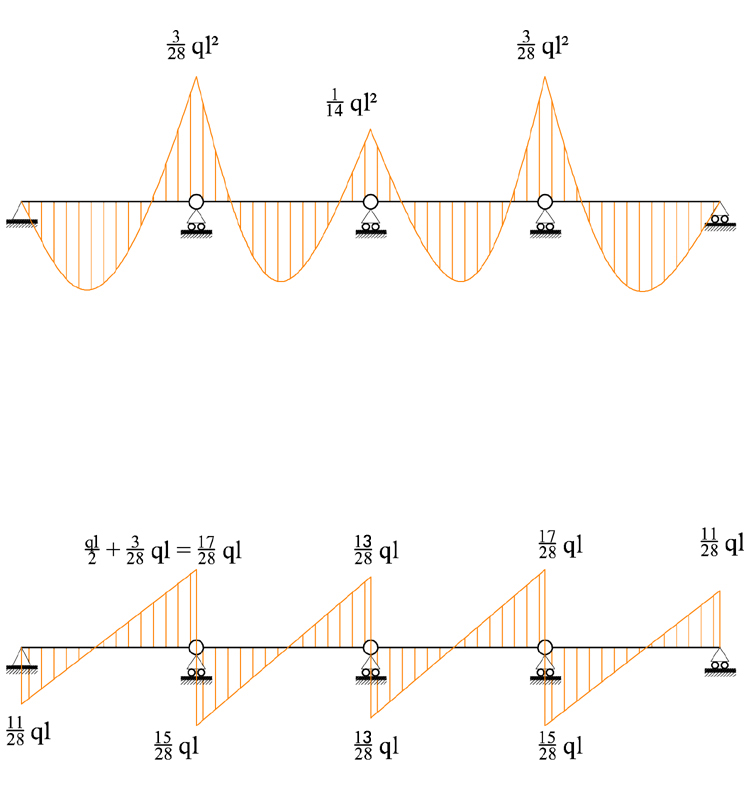
DIAGRAMMI MOMENTO E TAGLIO