Dimensionamento di massima di una trave inflessa

Sin dall’antichità il sistema più comune per ricoprire aperture è stato sicuramente il sistema trilitico (dal quale poi deriverà il sistema arcuato) il quale consiste in un elemento orizzontale rettilineo (architrave) disposto su due sostegni verticali puntiformi (piedritti).

In questo blog si vuole porre l’attenzione sull’elemento trave, effettuandone un dimensionamento di massima. Il calcolo ha come obiettivo quello di determinare l’altezza “h” della trave, mentre sono definiti i valori  della base della sezione “b”, del momento massimo agente “Mmax” e la resistenza di progetto “fd”.

Si impone, inoltre, che la resistenza di progetto sia uguale alla tensione massima del materiale:

σmax= fd

Il valore della tensione massima è data dalla formula di Navier per la flessione:

σmax =  (Mmax/ Ix) * ymax

dove:

ymax/Ix = Wx è il modulo di resistenza a flessione della sezione   →   σmax = Mmax/Wx

Avendo posto σmax= fd, il modulo di resistenza è il più basso che possiamo utilizzare.

Considerando:

Mmax = ql²/8 (trave doppiamente appoggiata)

Wx = bh³/12 / h/2  = bh²/6  (sezione rettangolare)

Si ha:

bh²/6 = ql²/8  / fd        →         h = rad(6 Mmax/b fd) * l

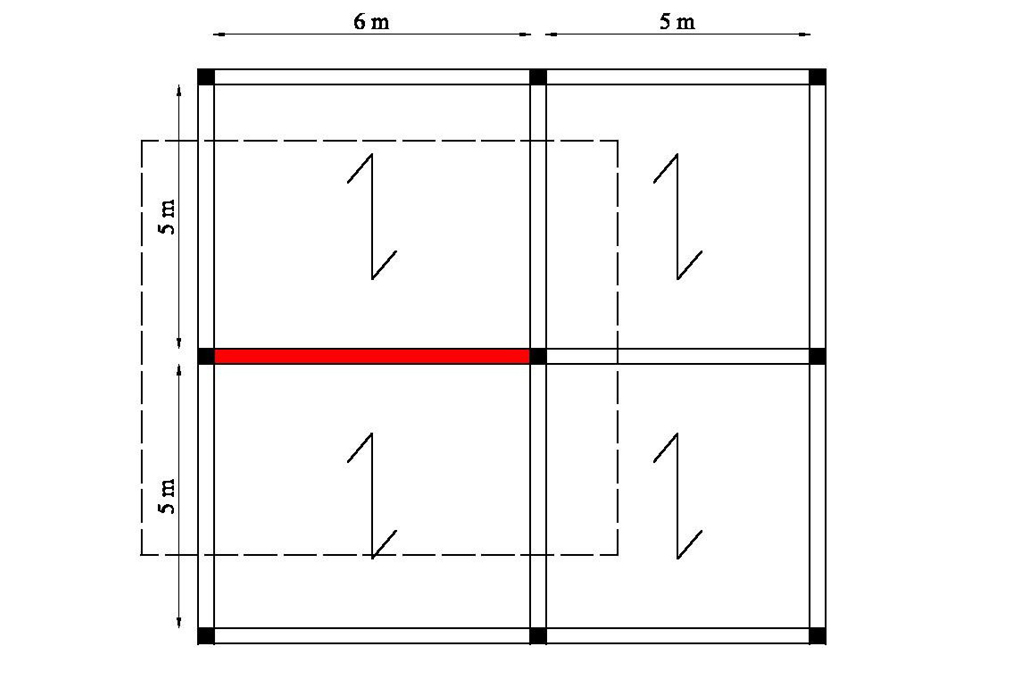
Esaminando un impalcato in legno, ordito come si vede in figura, scelgo di effettuare il dimensionamento della trave maggiormente sollecitata a flessione.

Di seguito, invece, viene definita la sezione del solaio.

La trave in esame è in legno lamellare GL36c a sezione rettangolare (cioè una classe di legno lamellare combinato con lamelle di qualità peggiori all’interno e di qualità migliore ai lembi superiore ed inferiore della sezione) con resistenza a flessione fm,k = 36 N/mm².

La resistenza di progetto è fd= Kmod * fm,k / γm

Kmod (coefficiente che dipende dalla durata del carico e dall’umidità) = 0,6

γm(coefficiente di sicurezza relativo al materiale) = 1,45

Analisi dei carichi

Carico strutturale qs

Trave legno lamellare GL36c: 1,00 m x 0,45 m x 0,30 m x 430 Kg/m³       = 58  Kg/m² = 0,58 kN/m²

Travicelli (abete): 2 x 1,00 m x 0,06 m x 0,10 m x 600 Kg/m³                  = 7,2     "     = 0,072    "

Tavolato (legno di abete) :  1,00 m x 1,00 m x 0,03 m x 600 Kg/m³            = 18      "     = 0,18      "

Carichi permanenti qp

Massetto :  1,00 x 1,00 m x 0,05 m x 1900 Kg/m³                                       = 95  Kg/m² = 0,95  kN/m²

Sottofondo Pavimento : 1,00 x 1,00 m x 0,03 m x 1800 Kg/m³                   = 54      "     = 0,54     "

Pavimento :  1,00 m x 1,00 m x 0,01 m x 400 Kg/m³                                 = 40      "      = 0,40     "

Incidenza tramezzi :                                                                                = 100     "     = 1,00     "

Incidenza impianti :                                                                                 =   50     "     = 0,50     "     

Carico d’esercizio qa

Locali d’abitazione                                                                                        200  Kg/m² = 2 kN/m²

                                                   Totale        622,9  Kg/m² ≈ 6,3 kN/m²

qtot = (qs+ qp+ qa) * interasse = 6,3 kN/m² * 5 m ≈ 31, 11 kN/m

A questo punto, essendo noto σmax,  Mmax e base della sezione, possiamo determinare il valore dell’altezza della sezione, utilizzando il seguente foglio di calcolo excel.

L'altezza assunta è di 45 cm.

Interessante è esaminare le dimensioni della trave inflessa considerandola sia in calcestruzzo armato che in acciaio. In questa operazione ipotizzo che i carichi agenti sulla trave siano gli stessi di quelli agenti sulla trave prima calcolata in legno lamellare (trascurando il peso proprio della trave stessa). Ovviamente i valori della luce e dell’interasse rimarranno invariati.

CALCESTRUZZO ARMATO

Mmax = ql²/8    con q = 6,3 kN/m

b = 30 cm

σmax = σca = α * Rck/γm

dove:

Rck = resistenza caratteristica calcestruzzo = 30 N/mm² (calcestruzzo ordinario di classe C 25/30)

α = coeff. riduttivo per la resistenza a lunga durata = 0,85

γm = coeff. riduttivo parziale di sicurezza relativo al cls = 1,5

σfa = fy/γs

dove:

fy = tensione di snervamento delle barre di acciaio = 450 N/mm²

γs = coeff. di sicurezza relativo all’acciao = 1,15

H = hu + δ

dove:

hu = altezza utile = r * rad(Mmax/b)

δ= distanza dal centro dei tondini al lembo inferiore della trave = 5 cm

ACCIAIO

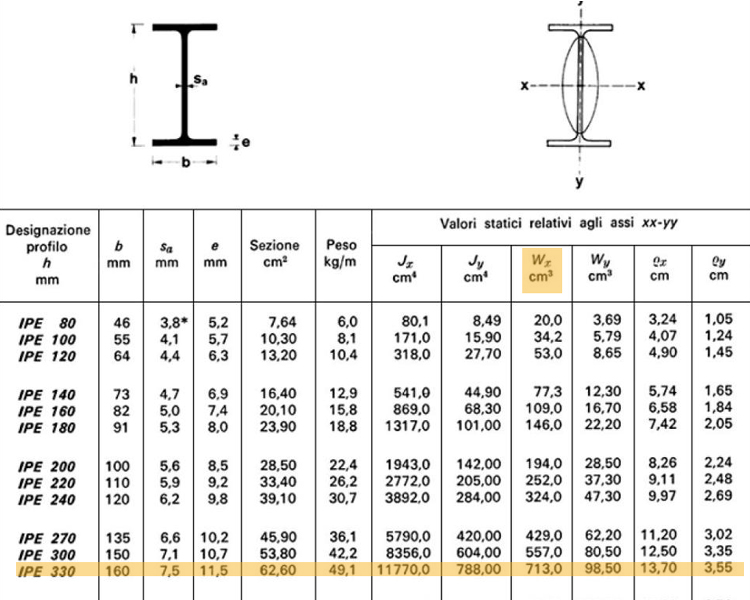
Nel caso dell’acciaio, calcolando il valore del modulo di resistenza Wx, in relazione alla base imposta in fase di progetto e momento agente sulla trave, si determina il profilo, scegliendolo dal profilario, in modo che questo abbia un modulo di resistenza maggiore o uguale rispetto a quello calcolato.

Mmax = ql²/8 con q = 6,3 kN/m

σmax  = σfa = fy/γs

dove:

fyk = tensione di snervamento caratteristica dell’acciao Fe 360= 235 N/mm²

γs = coeff. di sicurezza relativo all’acciao = 1,15

Wx = Mmax/σfa