Esercitazione_4 trave su più appoggi (risoluzione di un sistema iperstatico attraverso il metodo delle forze)

 

Esercitazione_4

trave su più appoggi (risoluzione di un sistema iperstatico attraverso il metodo delle forze)

 

 

1_

tipologia di esercizio

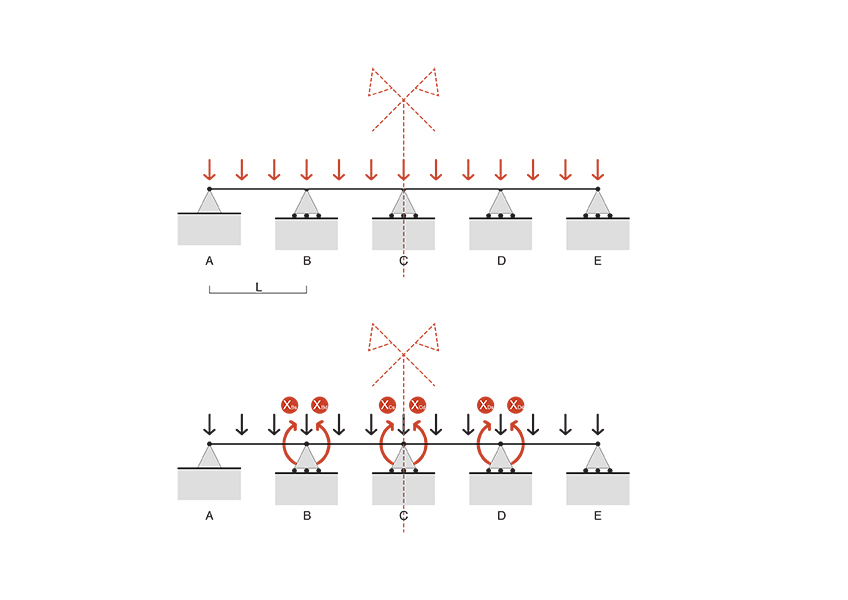
L’esercizio inquadra una struttura composta da una trave su più appoggi, la quale risulta di conseguenza iperstatica. Per procedere quindi con la risoluzione dello schema verrà applicato il metodo delle forze, il quale metodo prevede il declassamento dei vincoli, sostituendoli con forze o momenti, corrispondenti alle reazioni vincolari escluse dallo schema. Questo metodo ha come obbiettivo la risoluzione di uno schema iperstatico mediante schemi isostatici equivalenti.

 

2_

analisi della trave

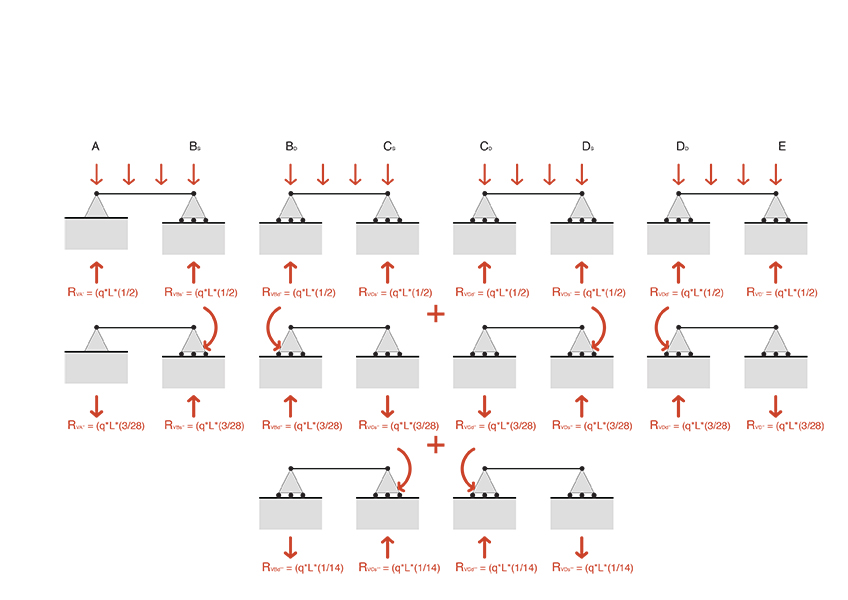
La scelta del declassamento dei vincoli viene definita dalla conoscenza del valore di abbassamento e rotazione (deformata della trave) sotto condizioni di carico distribuito o momenti flettenti. Per procedere quindi con la risoluzione dello schema iperstatico, si declassano le cerniere B-C-D, rendendole di conseguenza passanti (quindi interne) e aggiungendo delle coppie di momenti nei punti B-C-D. Le coppie di momenti riescono a ripristinare la condizione di vincolo esclusa precedentemente, garantendo di conseguenza una simmetria nella rotazione della cerniera interna.

 

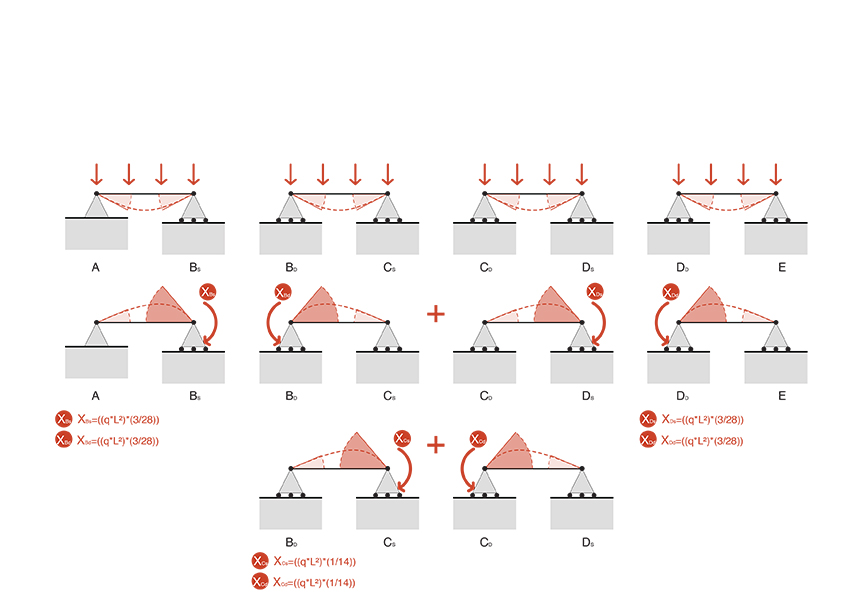
3_

equazioni di compatibilità cinematica

Successivamente vengono definite le equazioni di compatibilità cinematica della trave, dove abbiamo:

 

tratto A-B

ΔφB = ΔφD = 0 per simmetria dello schema trave

ΔφB = ΔφBs + ΔφBd ⇒ ΔφBs = ((q*L³)*(1/24*E*J)) - ((xBs*L)*(1/3*E*J))

⇒ ΔφBd = - ((q*L³)*(1/24*E*J)) + ((xBd*L)*(1/3*E*J)) + ((xCs*L)*(1/6*E*J))

ΔφBs = ((q*L³)*(1/24*E*J))-((xBs*L)*(1/3*E*J)) = -((q*L³)*(1/24*E*J))+((xBd*L)*(1/3*E*J))+((xCs*L)*(1/6*E*J)) = ΔφBd

⇒ ΔφB = ((q*L²)*(1/8)) - (ΔφC*(1/4))

tratto B-C

ΔφB = ΔφD = 0 per simmetria dello schema trave

ΔφC = 0

ΔφC = ΔφCs + ΔφCd ⇒ ΔφCs = ((q*L³)*(1/24*E*J)) - ((xBd*L)*(1/6*E*J)) - ((xCs*L)*(1/3*E*J))

⇒ ΔφCd = - ((q*L³)*(1/24*E*J)) + ((xDs*L)*(1/6*E*J)) + ((xCd*L)*(1/6*E*J))

ΔφCs = ((q*L³)*(1/24*E*J))-((xBd*L)*(1/6*E*J))-((xCs*L)*(1/3*E*J)) = -((q*L³)*(1/24*E*J))+((xDs*L)*(1/6*E*J))+((xCd*L)*(1/6*E*J)) = ΔφCd

⇒ Δφc = ((q*L²)*(1/14))

ΔφB = ((q*L²)*(1/8)) - (ΔφC*(1/4))

⇒ ΔφB = ((q*L²)*(1/8)) - (((q*L²)*(1/14))*(1/4))

⇒ ΔφB = ((q*L²)*(3/28))

 

 

4_

equazioni di equilibrio

Successivamente vengono definite le equazioni di equilibrio della trave, dove abbiamo:

 

 

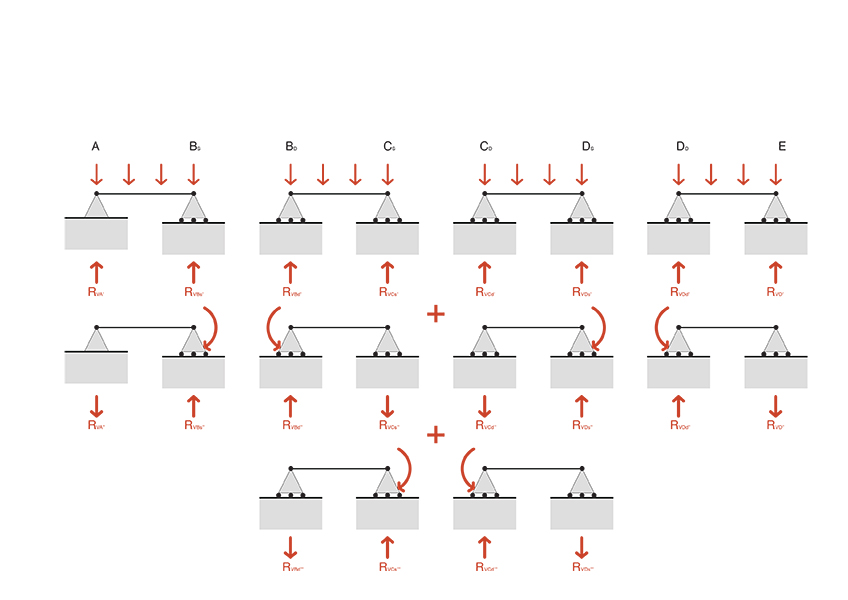
tratto A-B

RVA = (q*L*(1/2)) - (q*L*(3/28) ⇒ RVA = (q*L*(11/28))

RVBs = (q*L*(1/2)) + (q*L*(3/28) ⇒ RVBs = (q*L*(17/28))

 

tratto B-C

RVBd = (q*L*(1/2)) + (q*L*(3/28) - (q*L*(1/14) ⇒ RVBd = (q*L*(15/28))

RVCs = (q*L*(1/2)) - (q*L*(3/28) + (q*L*(1/14) ⇒ RVCs = (q*L*(13/28))

 

tratto C-D

RVCd = (q*L*(1/2)) - (q*L*(3/28) + (q*L*(1/14) ⇒ RVCd = (q*L*(13/28))

RVDs = (q*L*(1/2)) + (q*L*(3/28) - (q*L*(1/14) ⇒ RVDs = (q*L*(15/28))

 

tratto D-E

RVDd = (q*L*(1/2)) + (q*L*(3/28) - (q*L*(1/14) ⇒ RVCd = (q*L*(15/28))

RVE = (q*L*(1/2)) - (q*L*(3/28) ⇒ RVE = (q*L*(11/28))

 

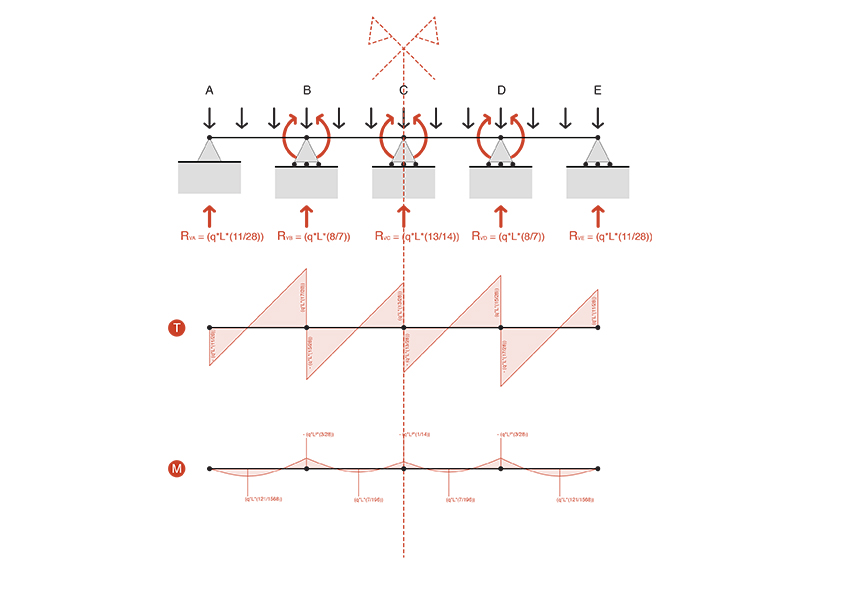
Successivamente vengono definite le reazioni vincolari complessive del sistema analizzato:

 

RVA = (q*L*(11/28))

RVBs = (q*L*(17/28)) ⎫

           +                 ⎬ ⇒ RVB = (q*L*(8/7))

RVBd = (q*L*(15/28)) ⎭

RVCs = (q*L*(13/28)) ⎫

           +                 ⎬ ⇒ RVC = (q*L*(13/14))

RVCd = (q*L*(13/28)) ⎭

RVDs = (q*L*(15/28)) ⎫

           +                 ⎬ ⇒ RVD = (q*L*(8/7))

RVDd = (q*L*(17/28)) ⎭

RVE = (q*L*(11/28))

 

 

5_

sollecitazioni di taglio e momento flettente

 

Successivamente vengono definite le sollecitazioni a taglio ed i punti di nullo del taglio, quest’ultimi eguagliando il valore del taglio nel dato tratto a 0 (sapendo che il punto di nullo definisce come suggerito dal nome il punto dove il taglio presenta un valore pari a 0):

 

taglio

tratto A-B

Ts = - (q*L*(11/28)) + q*s

s = 0 ⇒ T0 = - (q*L*(11/28))

s = L ⇒ TL = (q*L*(17/28))

Ts = 0 ⇒ - (q*L*(11/28)) + q*s = 0

⇒ s = L*(11/28)

 

tratto A-B + B-C

Ts = - (q*L*(11/28)) - (q*L*(8/7)) + q*s

s = L ⇒ TL = - (q*L*(15/28))

s = 2*L ⇒ T2L = (q*L*(13/28))

Ts = 0 ⇒ - (q*L*(11/28)) - (q*L*(8/7)) + q*L = 0

⇒ s = L*(15/28)

 

tratto A-B + B-C + C-D

Ts = - (q*L*(11/28)) - (q*L*(8/7)) - (q*L*(13/14)) + q*s

s = 2*L ⇒ T0 = - (q*L*(13/28))

s = 3*L ⇒ T0 = (q*L*(15/28))

Ts = 0 ⇒ - (q*L*(11/28)) - (q*L*(8/7)) - (q*L*(13/14)) + q*2*L = 0

⇒ s = L*(13/28)

 

tratto A-B + B-C + C-D + D-E

Ts = - (q*L*(11/28)) - (q*L*(8/7)) - (q*L*(13/14)) - (q*L*(8/7)) + q*s

s = 3*L ⇒ T0 = - (q*L*(17/28))

s = 4*L ⇒ T0 = (q*L*(11/28))

Ts = 0 ⇒ - (q*L*(11/28)) - (q*L*(8/7)) - (q*L*(13/14)) - (q*L*(8/7)) + q*3 = 0

⇒ s = L*(17/28)

 

momento

tratto A-B

Ms = ((q*L*(11/28))*s) - ((q*s²)*1/2)

s = 0 ⇒ M0 = 0

s = L ⇒ ML = - (q*L²*(3/28))

s = L*(11/28) ⇒ ML1 = (q*L*(121/1568))

 

tratto A-B + B-C

Ms = + (((q*L*(11/28))*(L+s)) + ((q*L*(8/7))*(s)) - ((q*(L+s)²*1/2)

s = 0 ⇒ M0 = - (q*L²*(3/28))

s = L ⇒ ML = - (q*L²*(1/14))

s = L*(15/28) ⇒ ML1 = (q*L*(7/196))

 

tratto A-B + B-C + C-D

Ms = + (((q*L*(11/28))*(2*L+s)) + (((q*L*(8/7))*(L+s)) + ((q*L*(13/14))*s) - ((q*(L+s)²* 1/2)

s = 0 ⇒ M0 = - (q*L²*(1/14))

s = L ⇒ ML = - (q*L²*(3/28))

s = L*(13/28) ⇒ ML1 = (q*L*(7/196))

 

tratto A-B + B-C + C-D + D-E

Ms = + (((q*L*(11/28))*(3*L+s)) + (((q*L*(8/7))*(2*L+s)) + (((q*L*(13/14))*(L+s)) + ((q*L*(8/7))*s) - ((q*(L+s)²*1/2)

s = 0 ⇒ M0 = - (q*L²*(3/28))

s = L ⇒ ML = 0

s = L*(11/28) ⇒ ML1 = (q*L*(121/1568))