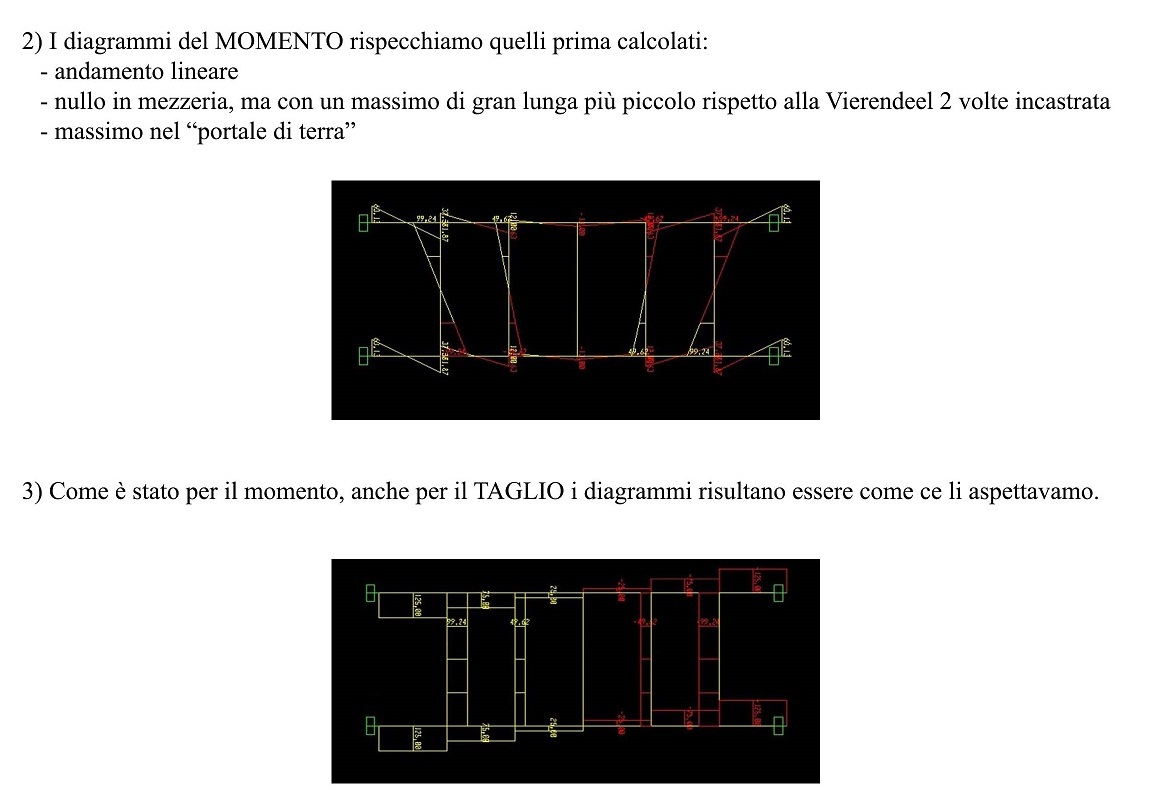
ESERCITAZIONE 5a - TRAVE VIERENDEEL 4 volte incastrata

La trave Vierendeel, dall'ingegnere che la brevettò, è una trave senza diagonali, composta da due correnti paralleli deformabili e montanti assialmente rigidi ortogonali ad essi. I nodi interni della trave devono essere in grado di trasmettere momenti flettenti (cosa che nelle travature reticolari non avviene, essendo essi delle cerniere).

Infatti la maglia triangolare è nel suo insieme indeformabile anche se sono ammesse rotazioni nei nodi, mentre quella rettangolare non lo è e quindi l'indeformabilità viene garantita con giunzioni in grado di impedire la rotazione reciproca tra le aste.

Studiamo il comportamento di questa trave sfruttando la sua simmetria: geometrica, dei carichi, dei vincoli e delle rigidezze.

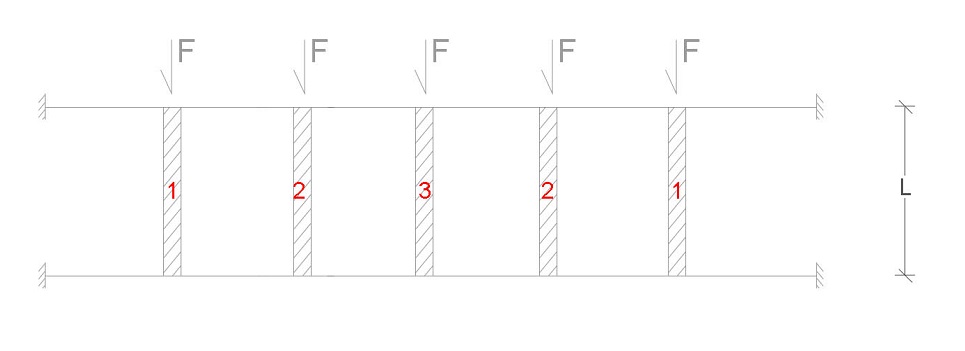
1) DETERMINAZIONE DEL TAGLIO NEGLI ELEMENTI ORIZZONTALI

Partiamo dall'elemento centrale (3) e procediamo verso sinistra (1):

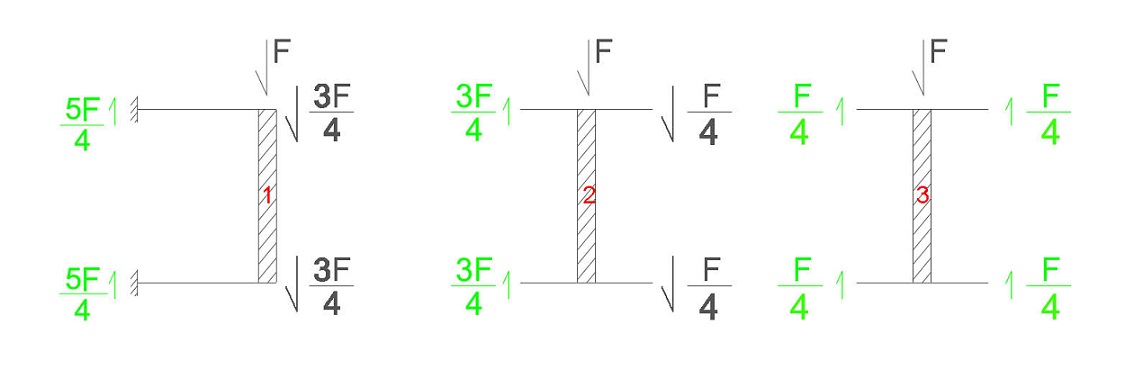
2) DISTRIBUZIONE DELLO SFORZO DI TAGLIO SUI CORRENTI:

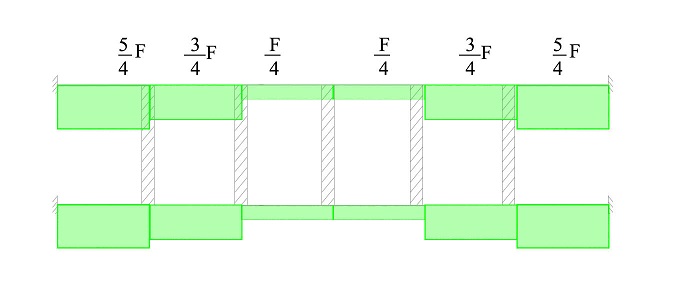
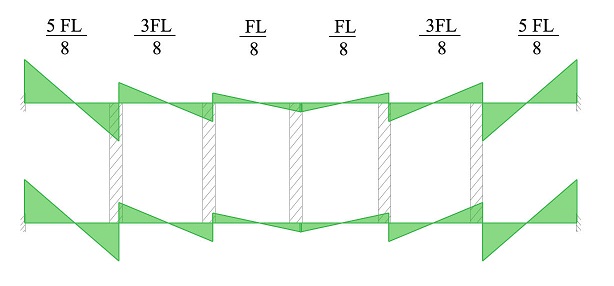
3) DISTRIBUZIONE DEL MOMENTO SUGLI ELEMENTI ORIZZONTALI

Per la determinazione del momento mi servo di questa semplice regola :

                                                                         M₀ = T * H/2      _{con H = L nel nostro caso}

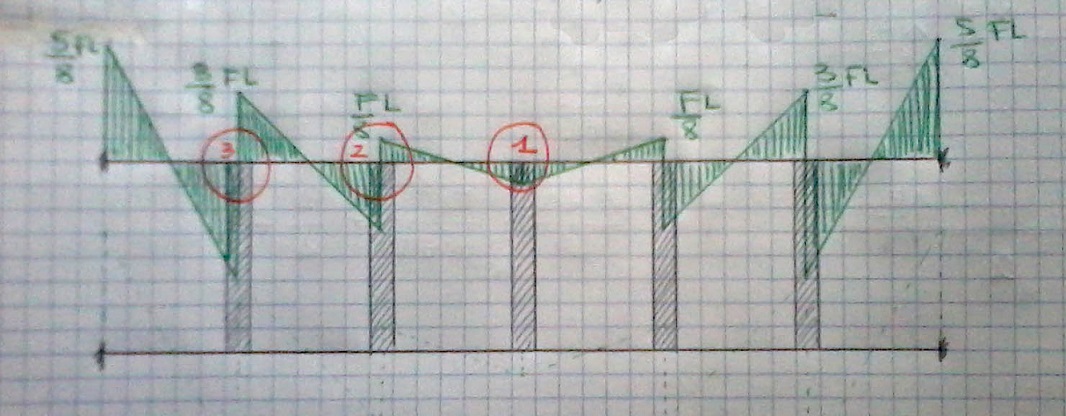
4) DETERMINAZIONE DEL MOMENTO NEI CORPI RIGIDI

Anche in questo caso la determinazione del momento è molto semplice, in quanto basta ribaltare i momenti che arrivano al nodo:

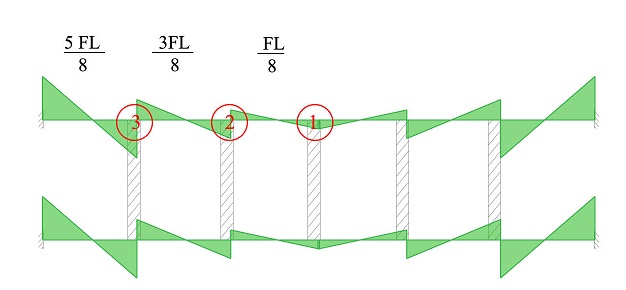
- NODO 1

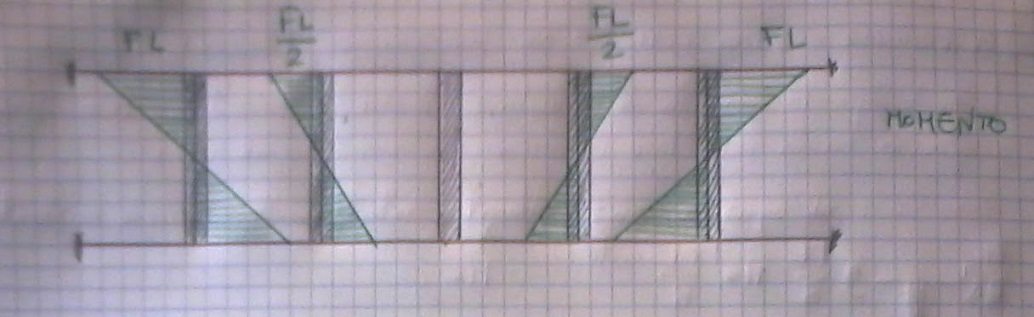
SAP