ESERCITAZIONE 5b TRAVE VIERENDEEL 2 volte incastrata
La trave Vierendeel, dall'ingegnere che la brevettò, è una trave senza diagonali, composta da due correnti paralleli deformabili e montanti assialmente rigidi ortogonali ad essi. I nodi interni della trave devono essere in grado di trasmettere momenti flettenti (cosa che nelle travature reticolari non avviene, essendo essi delle cerniere).
Infatti la maglia triangolare è nel suo insieme indeformabile anche se sono ammesse rotazioni nei nodi, mentre quella rettangolare non lo è e quindi l'indeformabilità viene garantita con giunzioni in grado di impedire la rotazione reciproca tra le aste.
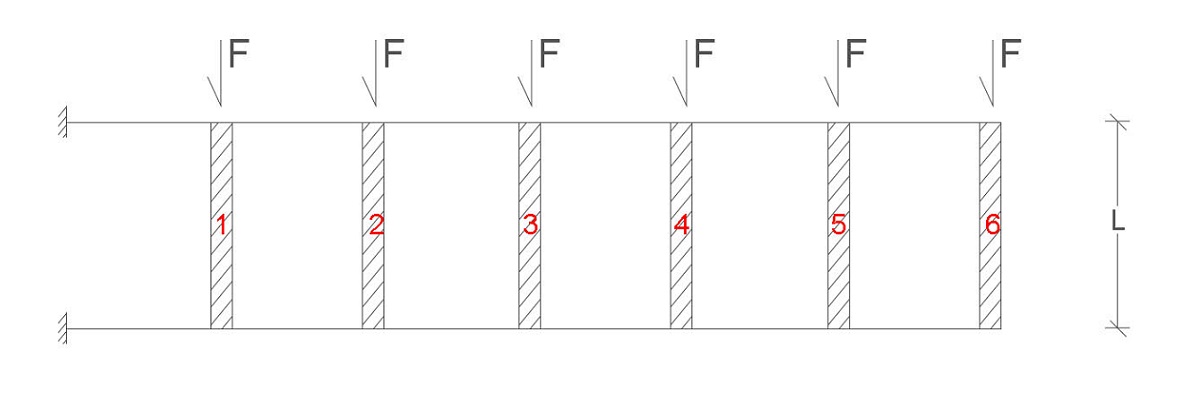
In questo esercizio NON possiamo sfruttare la simmetria, anche se i ragionamenti e il procedimento saranno del tutto analoghi all'esercizio precedente.
1) DISTRIBUZIONE DEL TAGLIO
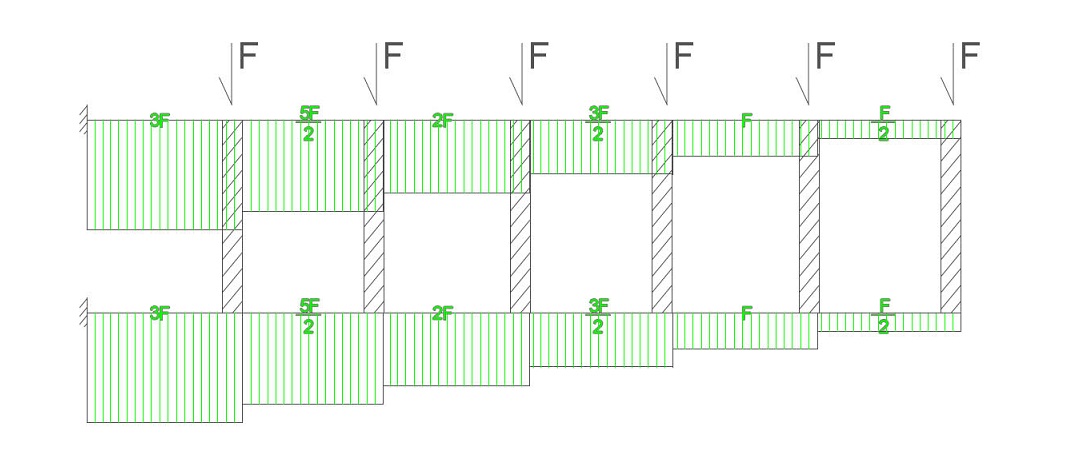
Le forze applicate si trasformano in taglio sulle travi, iniziamo dalla 6 procendendo verso sinistra:

Abbiamo quindi un diagramma del TAGLIO con andamento costante, come il precedente esercizio, ma che trova il suo massimo valore a 3F (nettamente superiore ai 3/4 F dell'esercizio con la trave 4 volte incastrata).
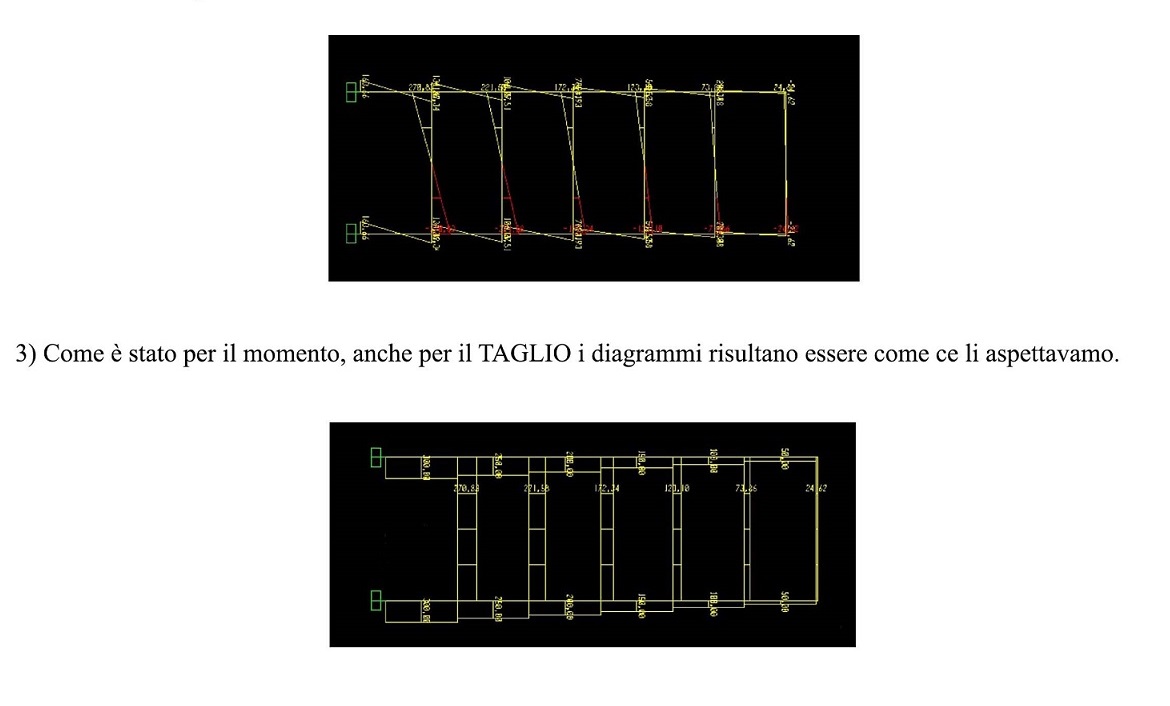
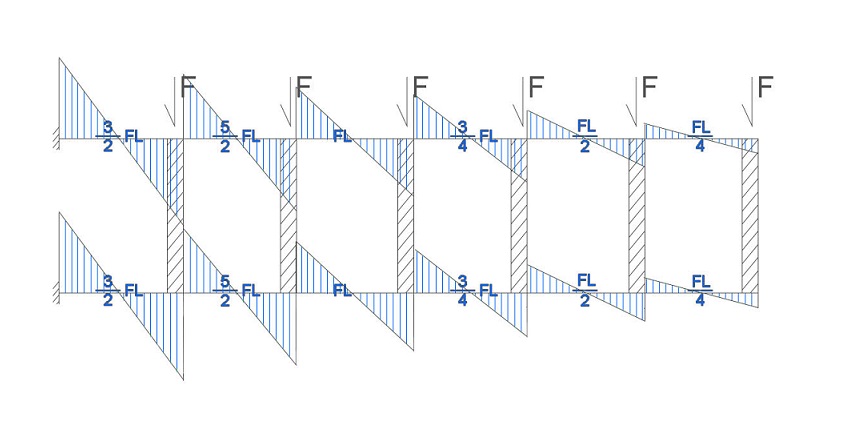
2) DISTRIBUZIONE DEL MOMENTO SUGLI ELEMENTI ORIZZONTALI
Anche in questo caso determiniamo il MOMENTO moltiplicando il taglio per metà della luce.
3) DISTRIBUZIONE DEL MOMENTO SUGLI ELEMENTI VERTICALI
Attraverso l'equilibrio dei NODI determiniamo il MOMENTO sui corpi rigidi:

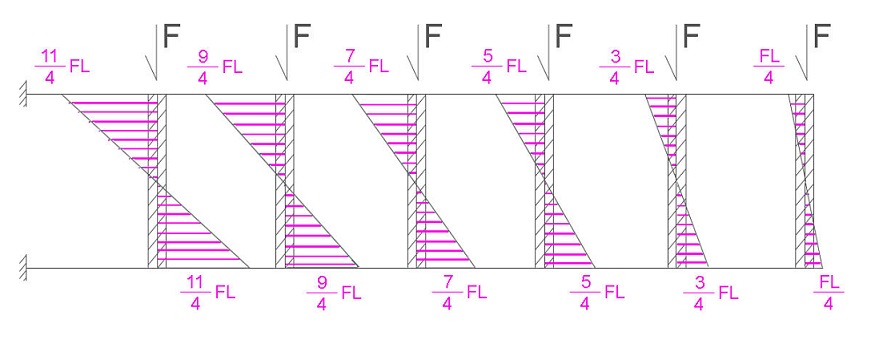
4) DISTRIBUZIONE DEL TAGLIO NEGLI ELEMENTI VERTICALI
Per determinare il TAGLIO sommiamo i momenti agenti sull'elemento e dividiamo per la sua luce. Il momento infatti dimensionalmente è una forza per una lunghezza, mentre il taglio una forza.
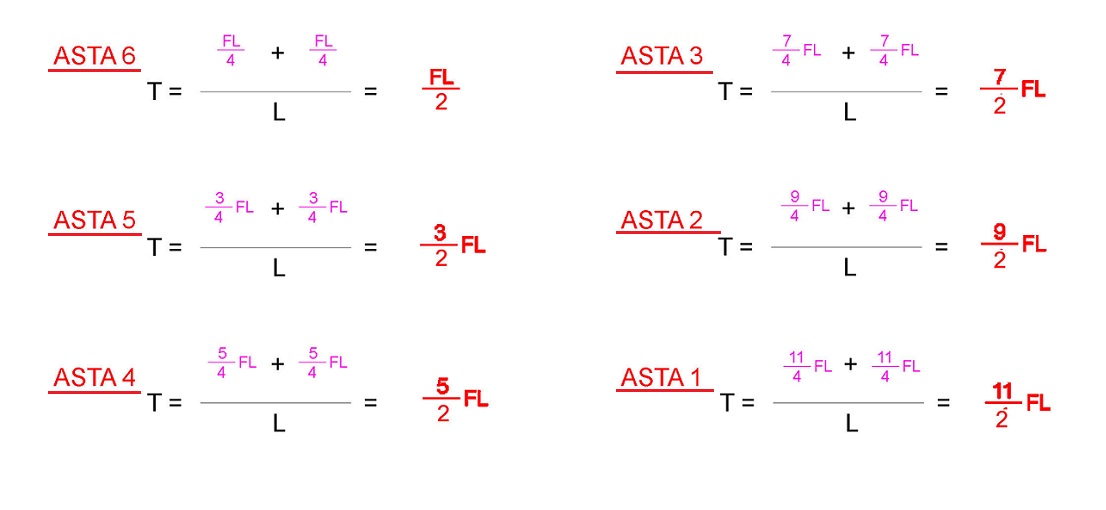
Possiamo quindi ora disegnare il diagramma:
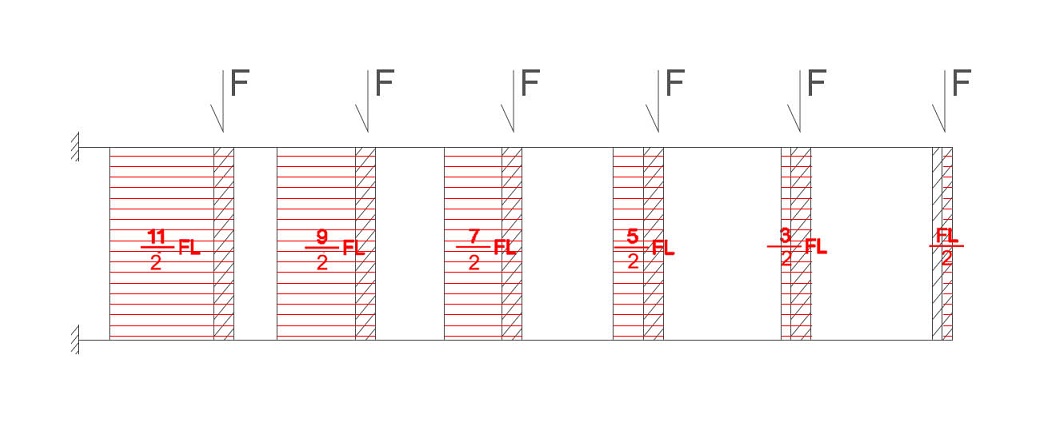
5) DEFORMATA E ABBASSAMENTO
La deformata, seguendo la conformazione del telaio SHEAR TYPE, avrà questa conformazione:
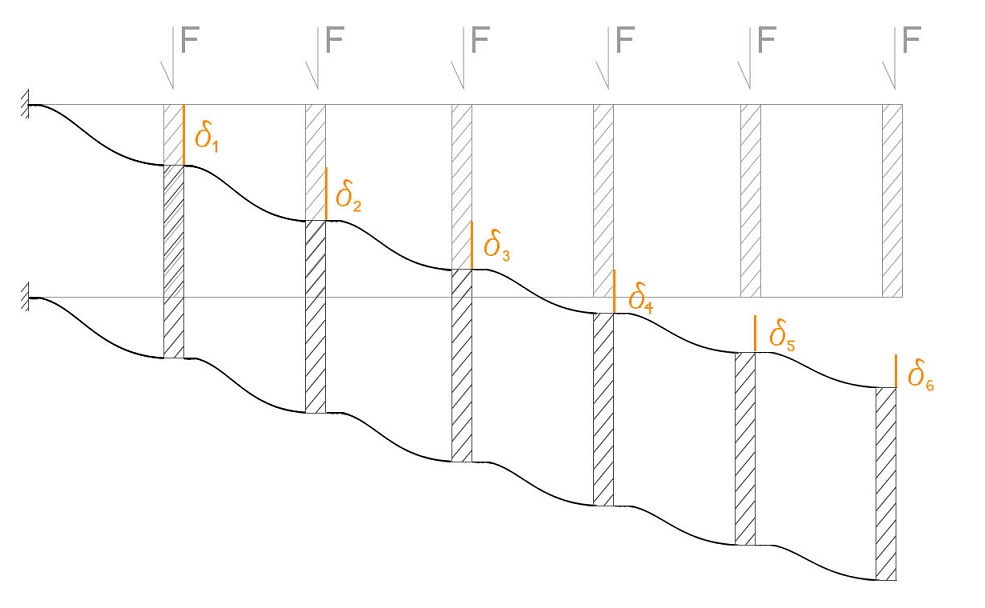
Lo spostamento δ dipende dal TAGLIO che sollecita l'asta (si prendono in considerazione i correnti superiore ed inferiore partendo dall'asta direttamente incastrata con l'esterno del sistema); sappiamo infatti che:
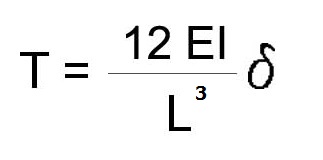
e quindi, svolgendo i calcoli, troveremo che:
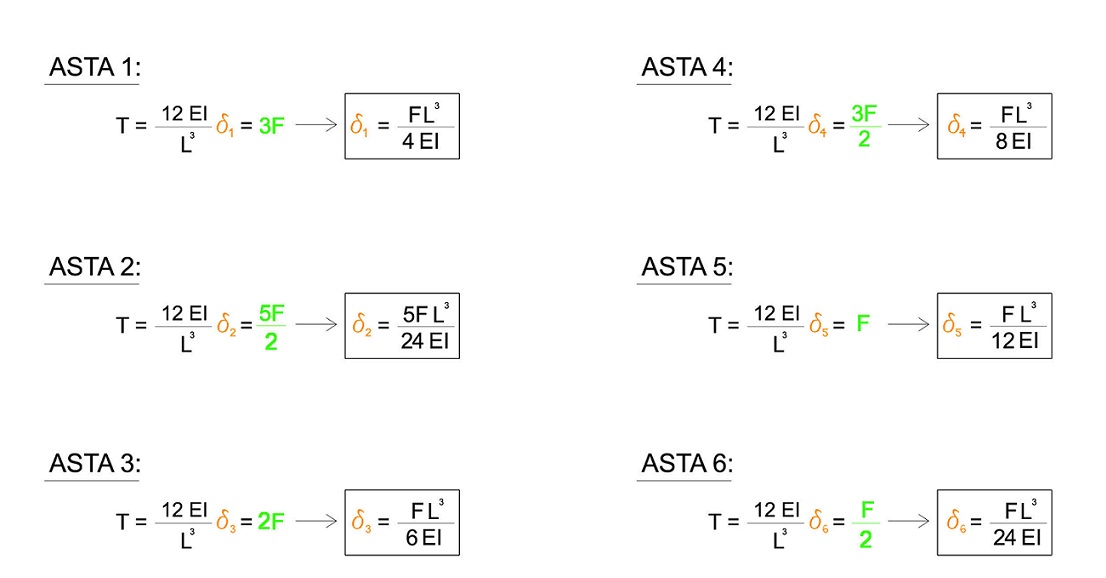
Questo vuol dire che l'ELEMENTO 1 (il primo sulla sinistra) subisce una deformazione 6 volte MAGGIORE di quella dell'ELEMENTO 6 (l'ulitmo a destra).