TRAVE VIERENDEEL - MENSOLA
METODO DELLE RIGIDEZZE – MENSOLA
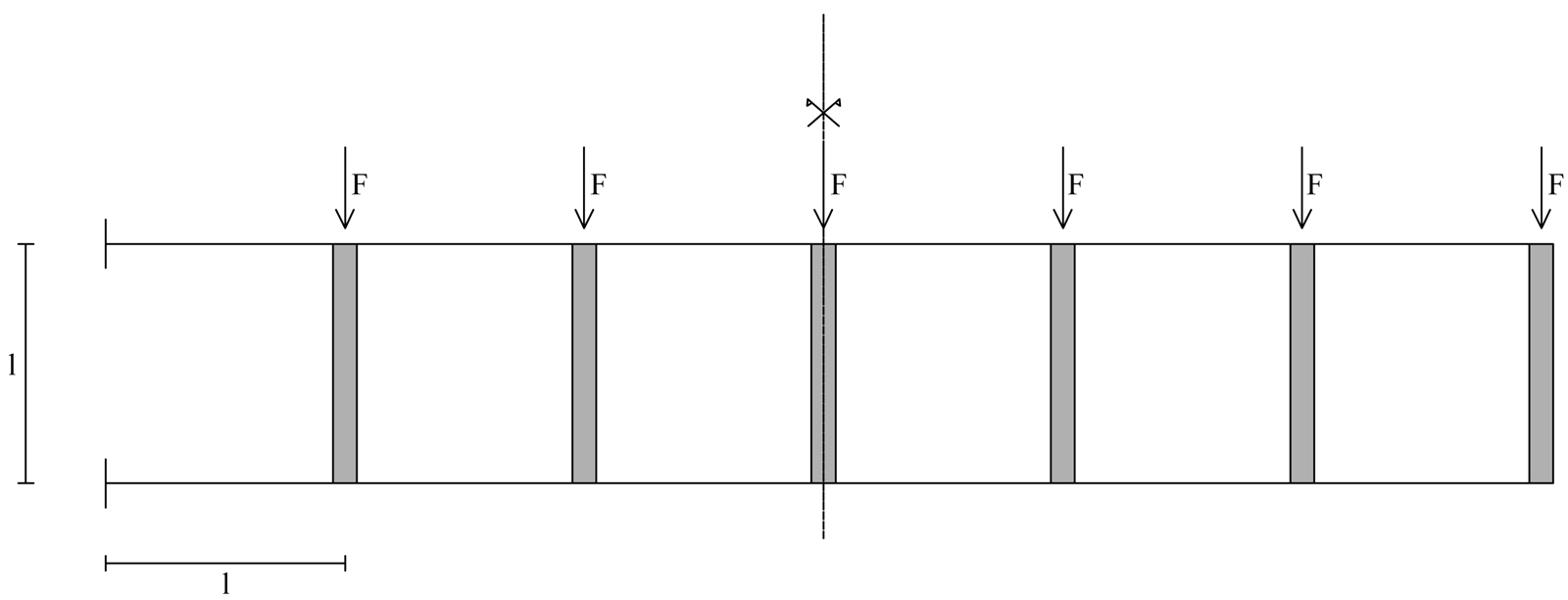
Questa è una trave Vierendeel ed ha lo stesso comportamento di un telaio shear-type ( travi infinitamente rigide e quindi resistenti a flessione). Mentre i pilastri sono soggetti a traslazioni provenienti da azioni esterne.
Questo telaio si deformerebbe così
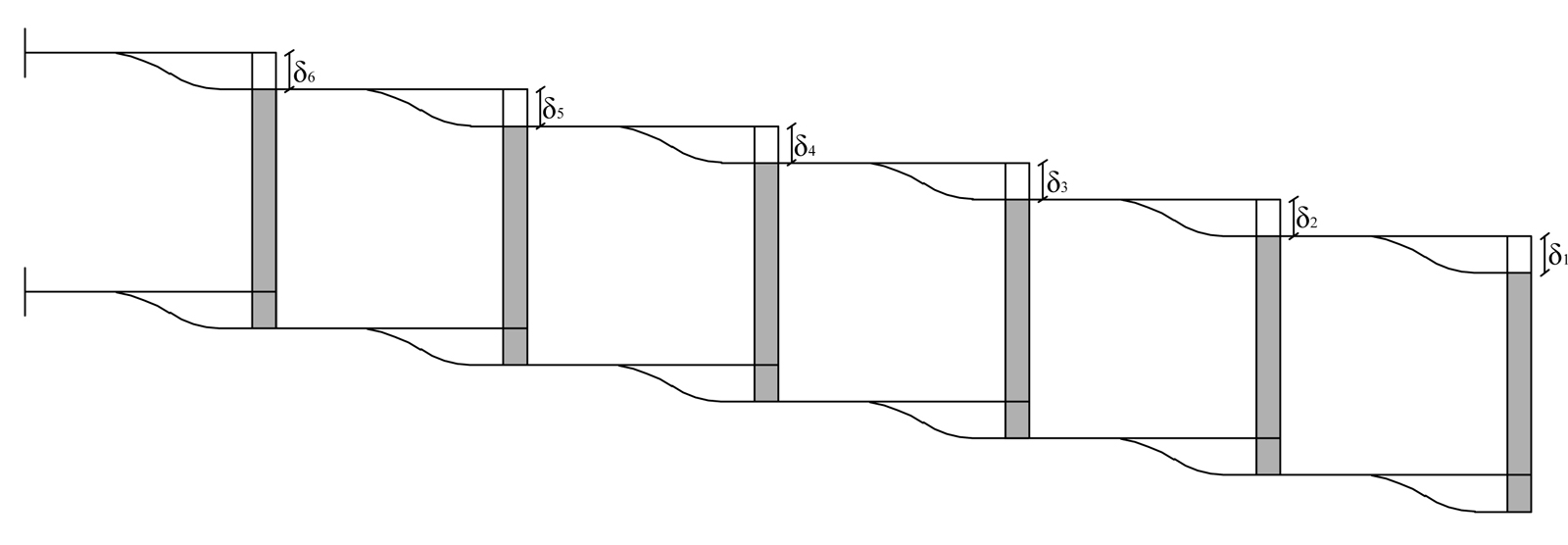
Questo solaio può essere visto come uno shear-type ruotato di 90°.
Consideriamo i tratti verticali come travi doppiamente appoggiate.
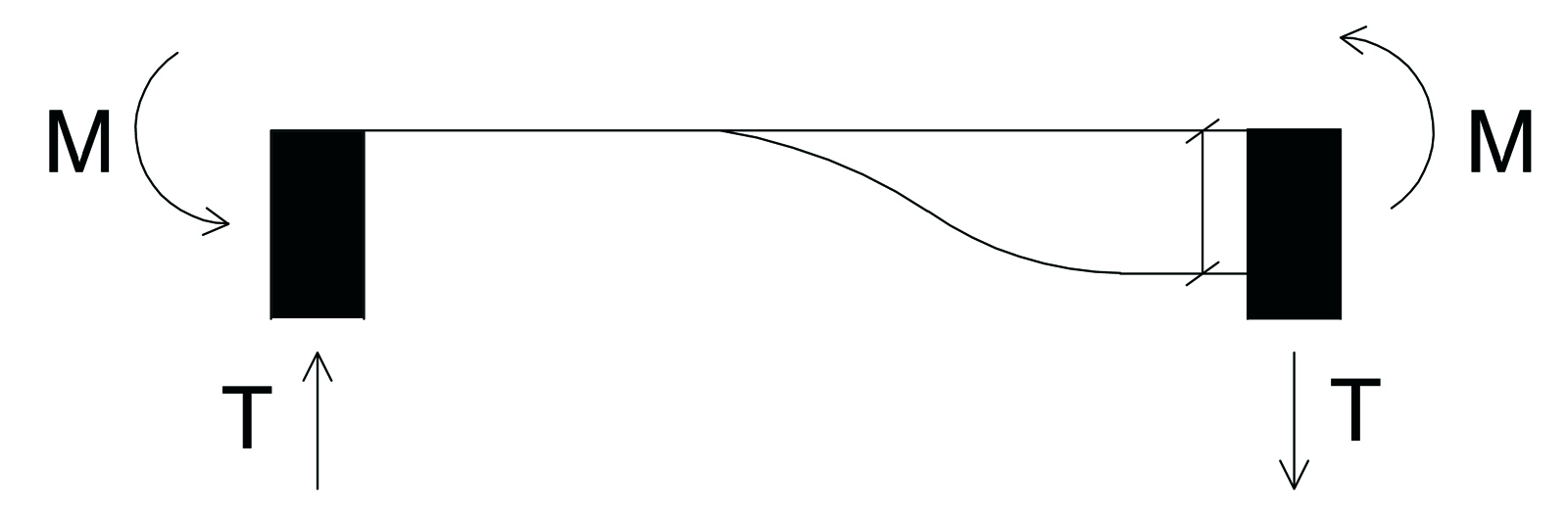
Questa trave è iperstatica ed è soggetta ad un cedimento vincolare δ, da cui si ricavano i seguenti valori del taglio e del momento:
M = 6 EI/l² * δ T = 12 EI/l³ * δ
TRATTO 1

-F + 2T = 0
F = 2T
Applicando i valori notevoli
F = 2 (12 EI/l³ * δ1) = 24 EI/ l³ * δ1
δ1 = F l³/24 EI
T = 12 EI/ l³ * δ1 = F/2
M = 6 EI/ l² * δ1 = Fl/4
TRATTO 2
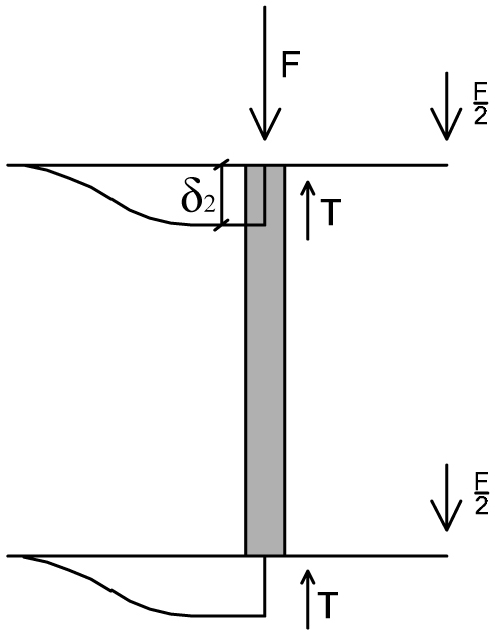
T + T – F – F/2 – F/2 = 0
2F = 2T
Applicando i valori notevoli
F = 12EI/ l³ * δ2
δ2 = F l³/12 EI
T = 12 EI/ l³ * δ2 = F
M = 6 EI/ l² * δ2 = FL/2
TRATTO 3

T + T – F -F – F = 0
3F = 2T
Applicando i valori notevoli
3F = 24 EI/l³ * δ3
δ3 = Fl/8 EI
T = 12 EI/ l³ * δ3 = 3/2 F
M = 6 EI/ l² * δ3 =3/4Fl
TRATTO 4
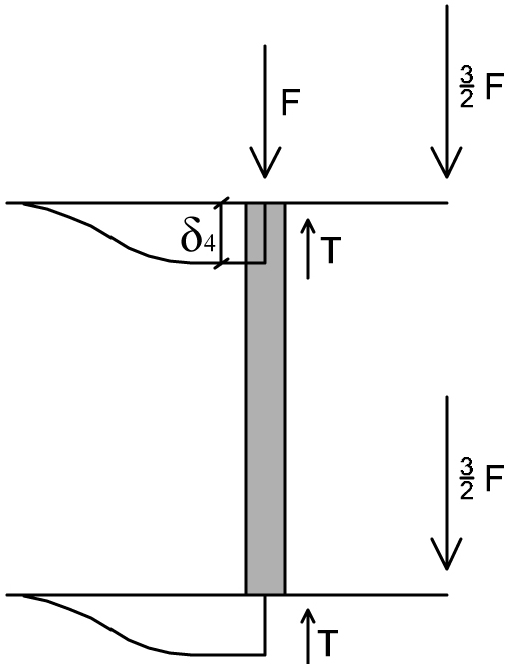
T + T – F – 3/2 F – 3/2 F = 0
4F = 2T
Applicando i valori notevoli
4 F = 24EI/ l³ * δ4
δ4 = F l³/6EI
T = 12 EI/ l³ * δ4 = 2F
M = 6 EI/ l² * δ4 = Fl
TRATTO 5
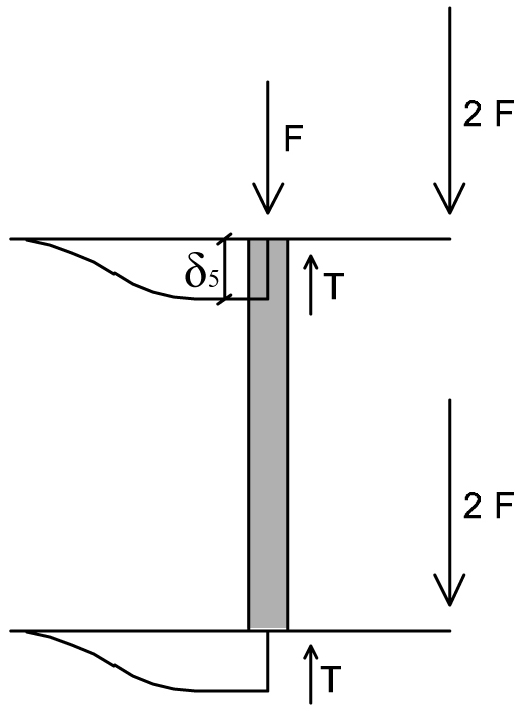
T + T – F – 2F – 2F = 0
5F = 2T
Applicando i valori notevoli
5F = 24 EI/ l³ * δ5
δ5 = 5 F l³/24 EI
T = 12 EI/ l³ * δ5 = 5/2 F
M = 6 EI/ l² * δ5 = 5/4 Fl
TRATTO 6
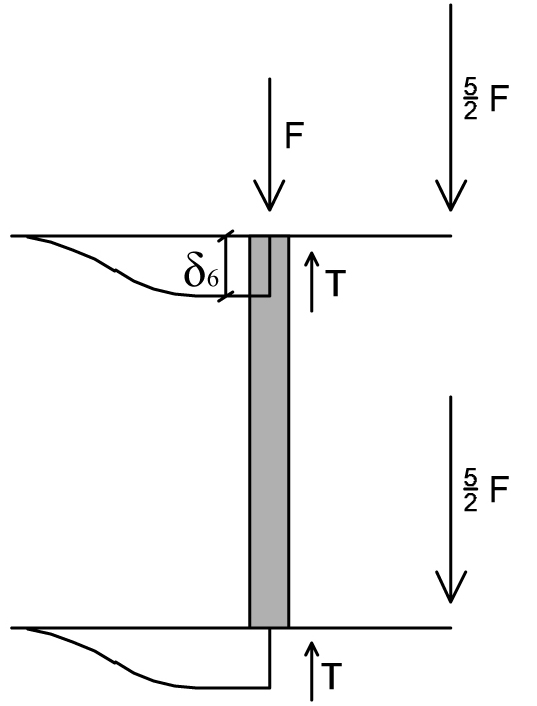
T + T – F – 5/2 F – 5/2 F = 0
6F = 2T
Applicando i valori notevoli
6F = 24 EI/ l³ * δ6
δ6 = F l³/4 EI
T = 12 EI/ l³ * δ6 = 3F
M = 6 EI/ l² * δ6 = 3/2 Fl
DIAGRAMMA DEL TAGLIO
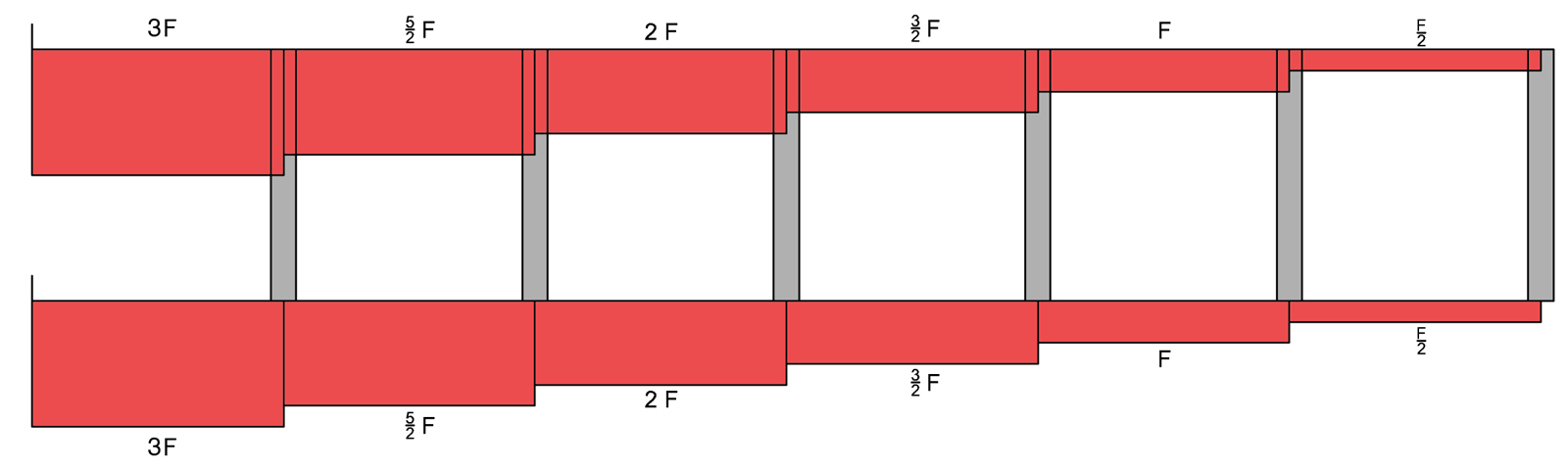
DIAGRAMMA DEL MOMENTO
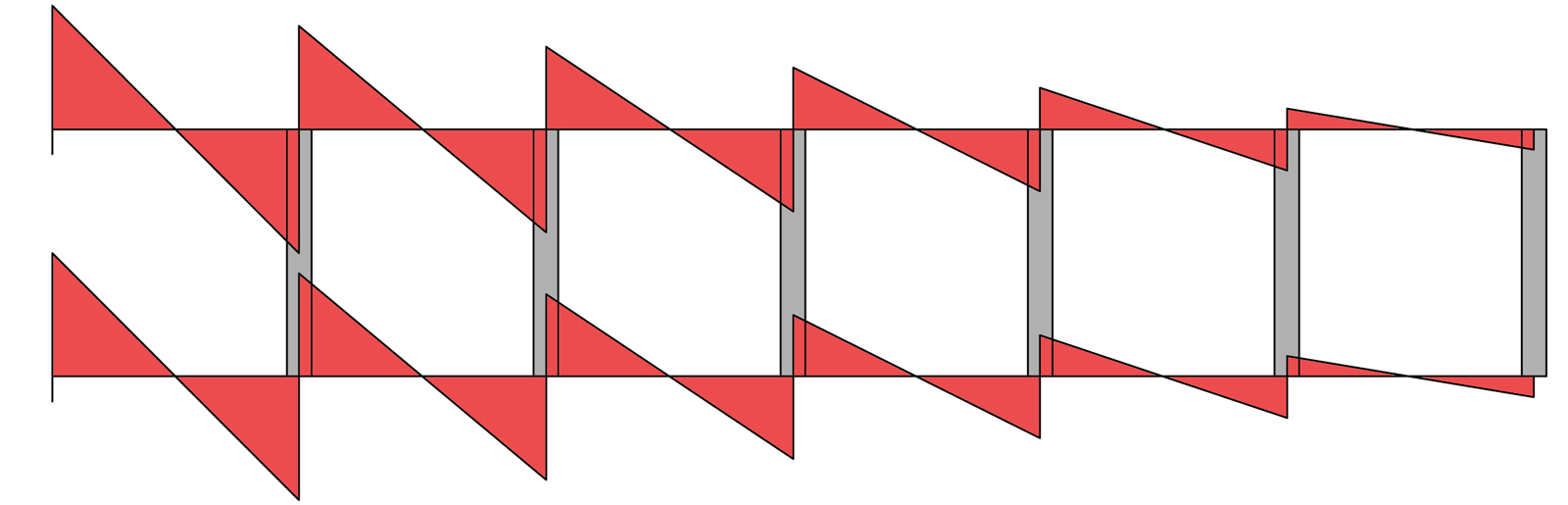
Ora bisogna calcolare il taglio e i momenti delle shear-type facendo l'equilibrio ai nodi
MOMENTI
TRATTO 1 VERTICALE
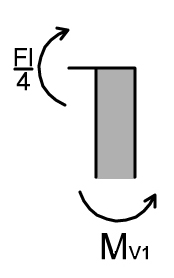
MV1 – Fl/4 = 0
MV1 = Fl/4
TRATTO 2 VERTICALE
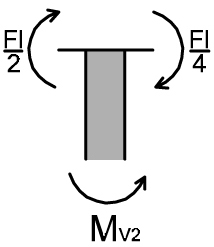
MV2 – Fl/4 – Fl/2 = 0
MV2 = 3/4Fl
TRATTO 3 VERTICALE
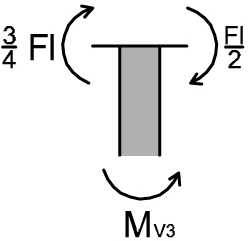
MV3 – 3/4Fl – Fl/2 = 0
MV3 = 5/4 Fl
TRATTO 4 VERTICALE
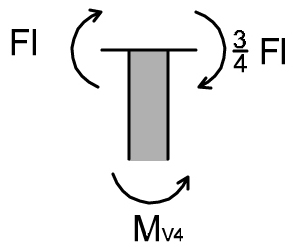
MV4 – Fl – 3/4Fl = 0
MV4 = 7/4 Fl
TRATTO 5 VERTICALE
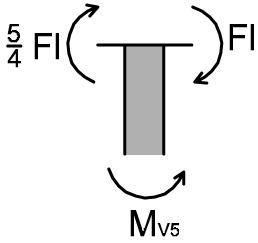
MV5 – Fl – 5/4 Fl = 0
MV5 = 9/4 Fl
TRATTO 6 VERTICALE
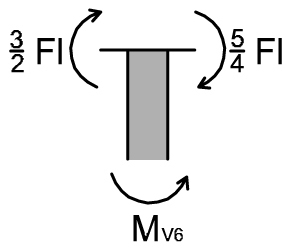
MV6 - 5/4 Fl – 3/2 Fl = 0
MV6 = 11/4 Fl
DIAGRAMMA MOMENTI VERTICALI
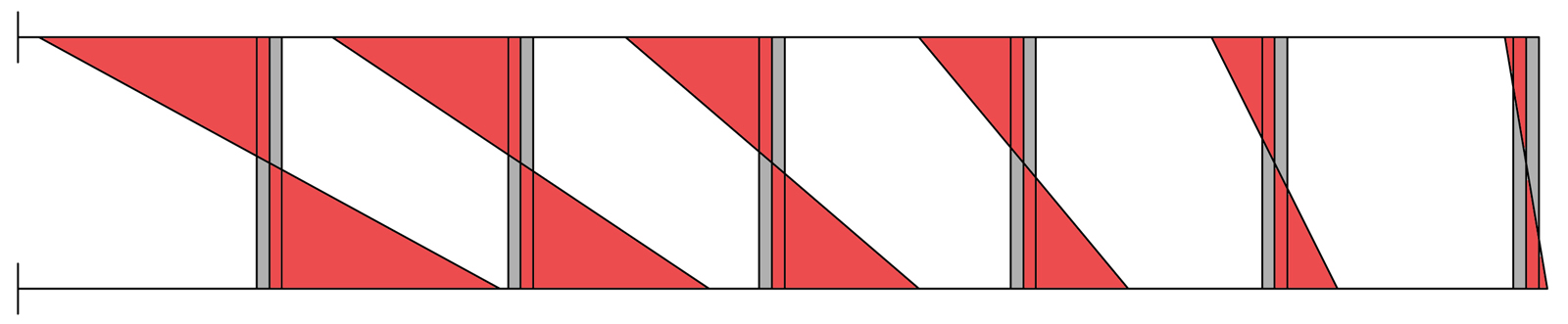
Per ricavarci i valori del taglio a questo punto ci basterà fare la somma dei momenti agenti sull'asta dividendoli per la luce e mettendo il taglio in equilibrio
TAGLIO
TRATTO 1 VERTICALE
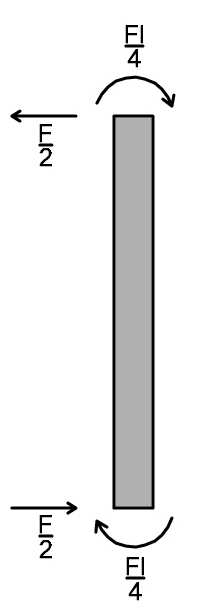
Tv1 = (Fl/4 + Fl/4) 1/l = F/2
TRATTO 2 VERTICALE
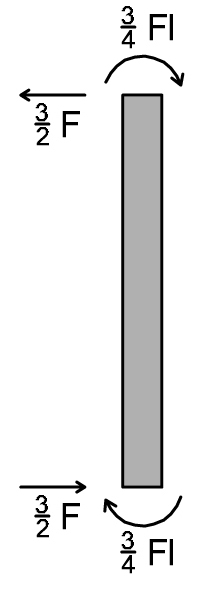
Tv2 = (3/4Fl + 3/4Fl) 1/l = 3/2F
TRATTO 3 VERTICALE
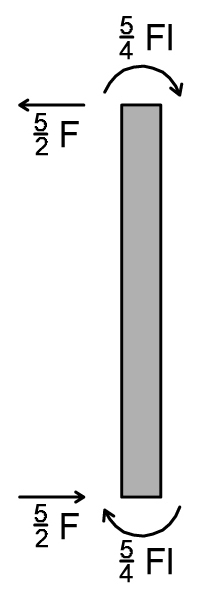
Tv3 = (5/4Fl + 5/4Fl) 1/l = 5/2 F
TRATTO 4 VERTICALE
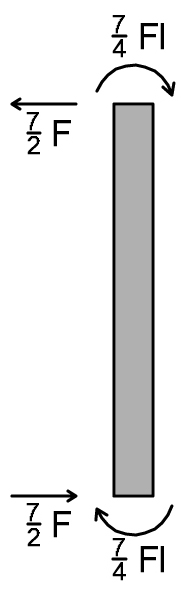
Tv4 = 7/4Fl + 7/4Fl) 1/l = 7/2 F
TRATTO 5 VERTICALE
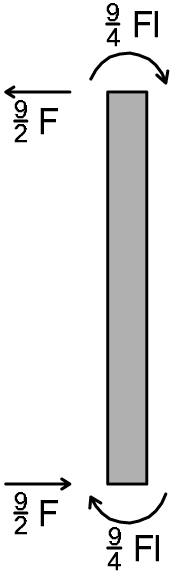
Tv5 = (9/4 Fl + 9/4Fl) 1/l = 9/2 F
TRATTO 6 VERTICALE
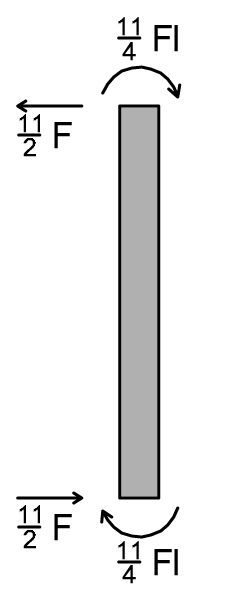
Tv6 = (11/4 Fl + 11/4 Fl) 1/l =11/2 F
DIAGRAMMA TAGLIO VERTICALE
Gli sforzi di taglio in un tratto diventano sforzi normali per i tratti ortogonali adiacenti, quindi possiamo disegnare il diagramma dello sforzo normale
DIAGRAMMA SFORZO NORMALE
