6_Ripartizione delle forze sismiche

In questa esercitazione, analizzeremo il comportamento di un impalcato strutturale soggetto a spinte orizzontali (ad esempio il vento o il sisma).

L’insieme di travi e pilastri, non solo riescono a resistere alle forze verticali ma se disposti correttamente nello spazio, possono anche fungere da controvento. I telai agiscono dunque come vincoli elastici, reagendo alle forze orizzontali lungo il loro stesso piano e proporzionalmente alla oro rigidezza, queste caratteristiche ci permettono di rappresentarli come vere e proprie molle!

A questo punto, consideriamo un impalcato in calcestruzzo armato (E=21000 N/mmq) composto da quattro  telai lungo X e quattro lungo Y, sorretti da dodici pilastri, questi ultimi avendo una dimensione di 30x40 cm e due momenti d’inerzia, uno lungo X e uno lungo Y.

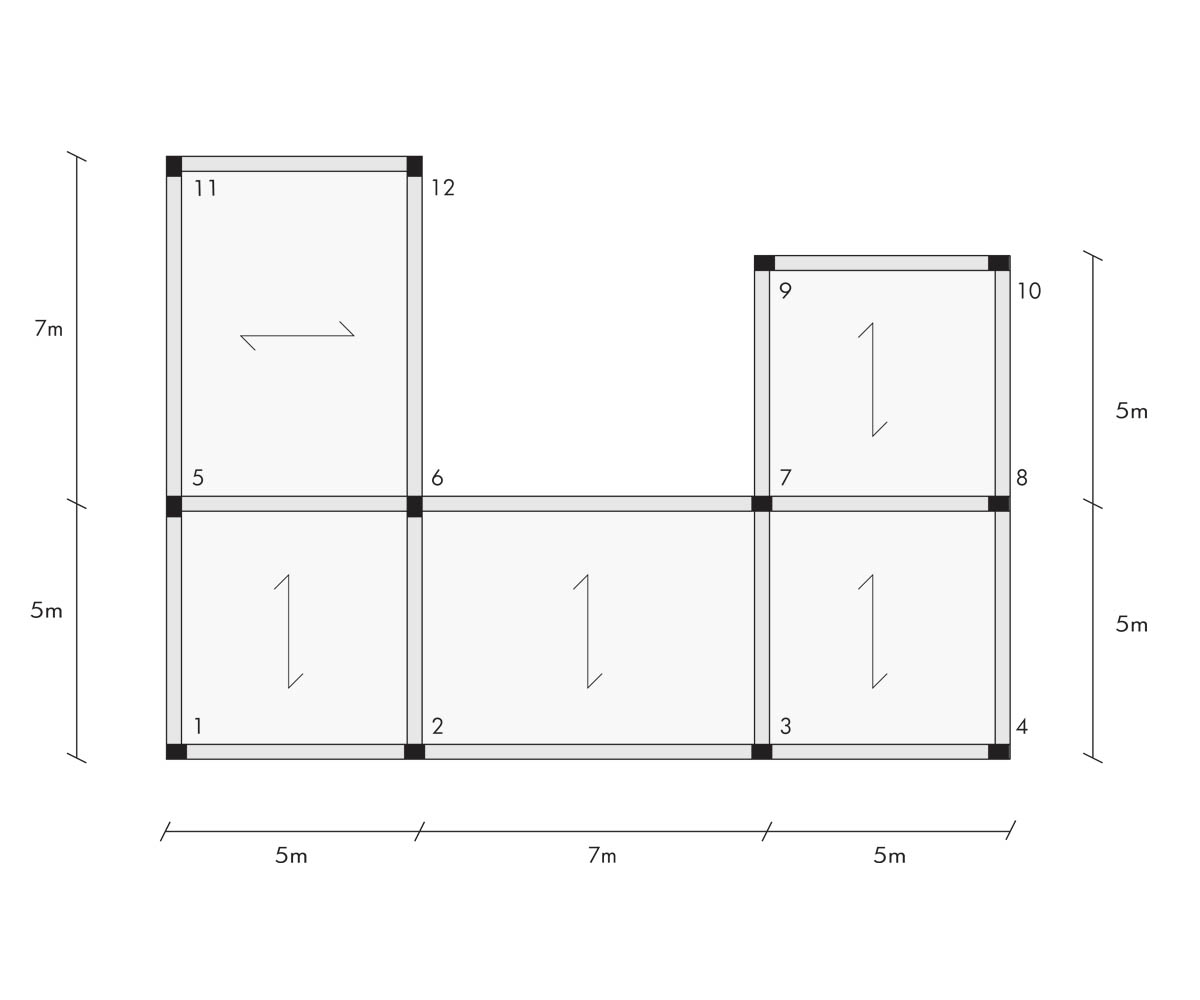
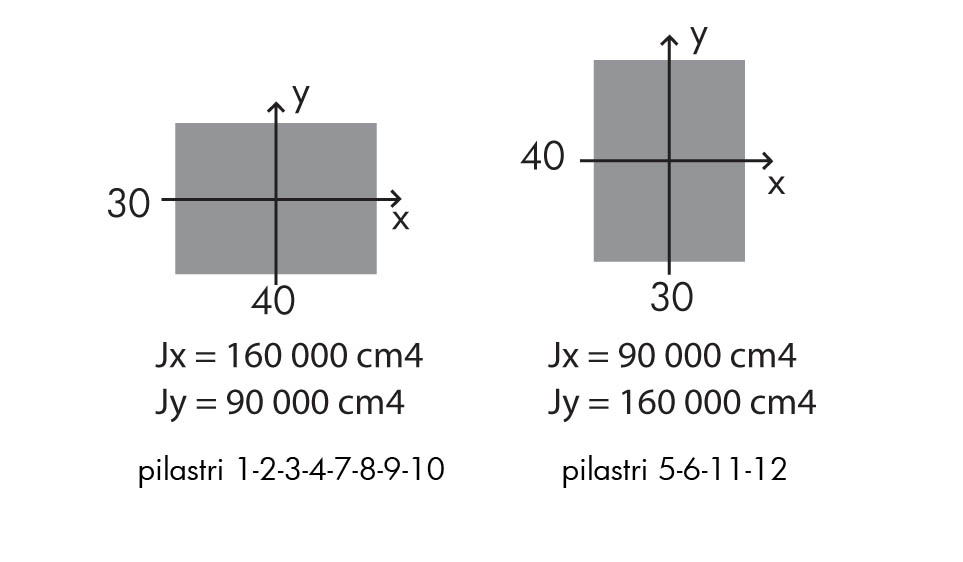
Ora riportiamo lo stesso impalcato con rappresentate le molle e le loro distanze dall’origine.

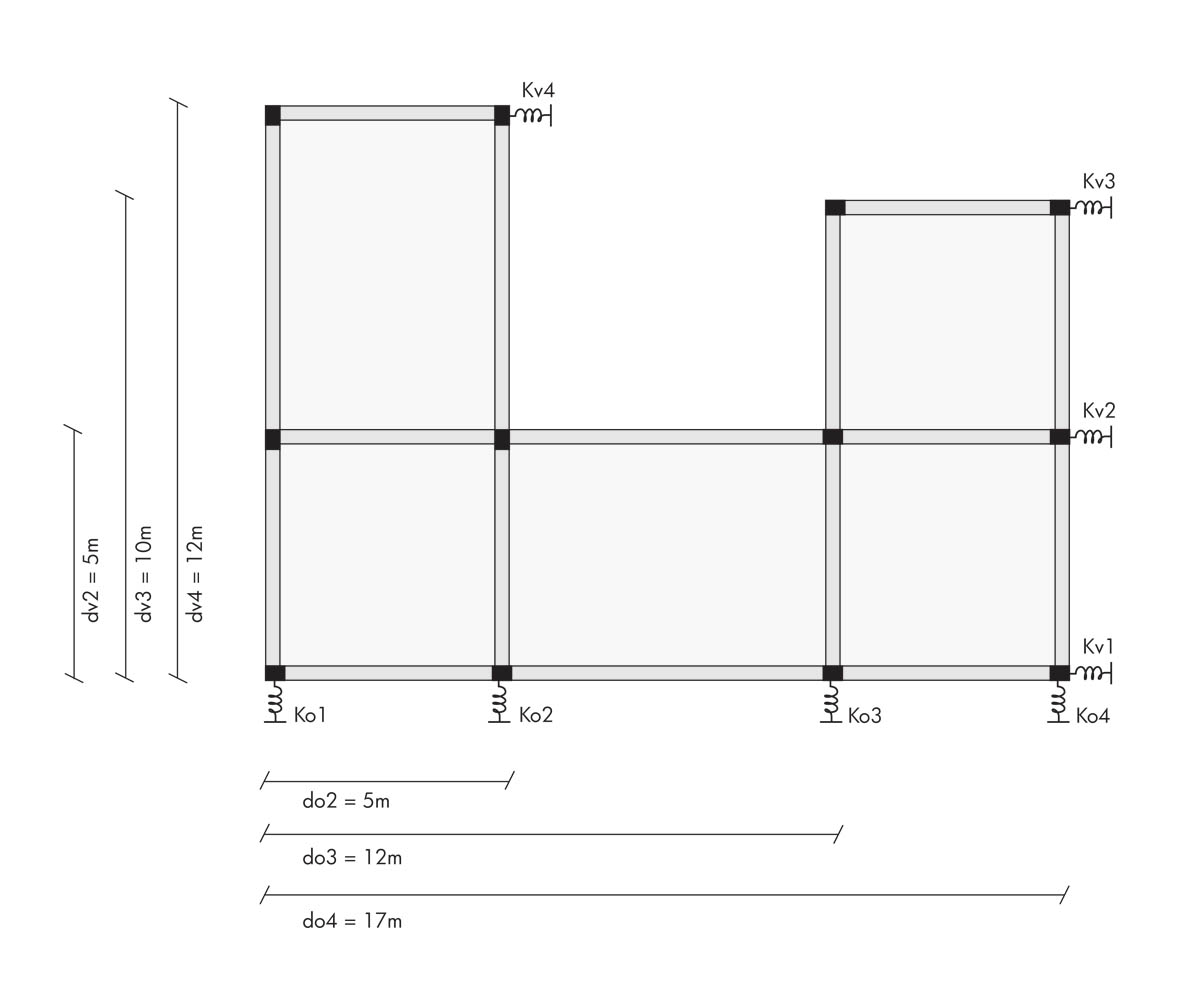
Passiamo al foglio Excel grazie al quale ci ricaveremo i valori di reazione alle forze sismiche:

STEP 1: CALCOLO DELLE RIGIDEZZE TRASLANTIDEI CONTROVENTI DELL’EDIFICIO.

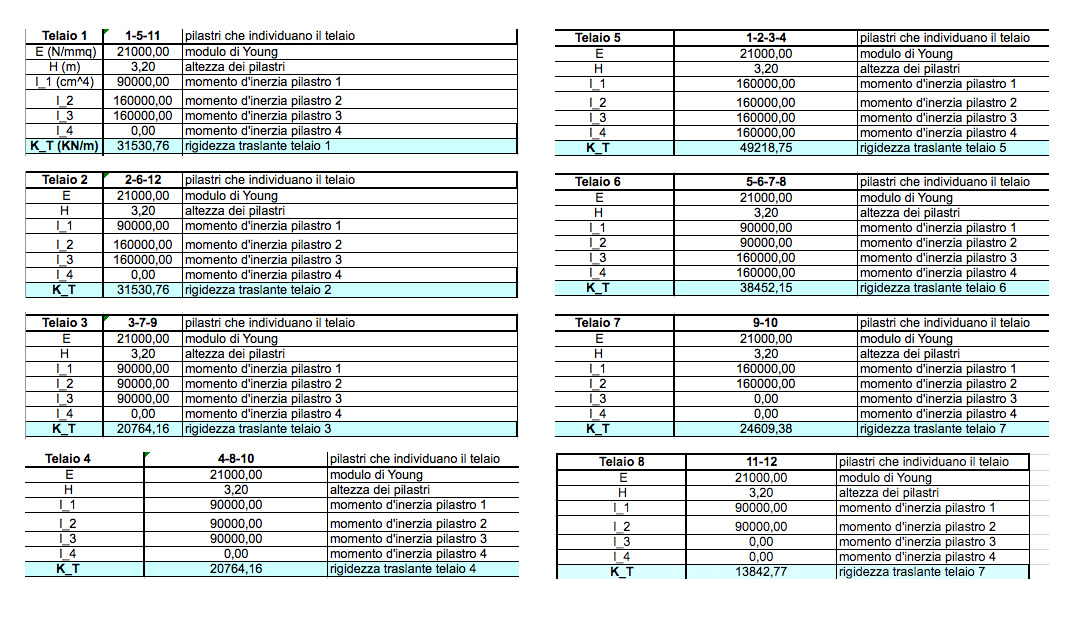
In queste tabelle inseriamo i valori di modulo elastico, dell’altezza dei pilastri e dei momenti d’inerzia dei pilastri (prendendo ovviamente quelli lungo l’asse del telaio studiato) per ricavarci la rigidezza traslante di ciascun telaio.

STEP 2: TABELLA SINOTTICA CONTROVENTI E DISTANZE.

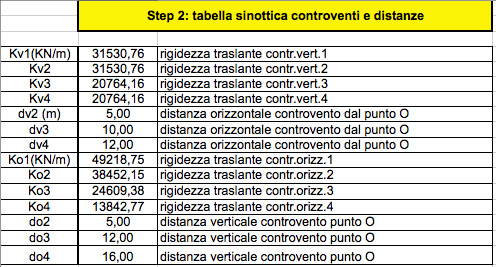
Qui riportiamo le distanze verticali e orizzontali dei controventi dall’origine O.

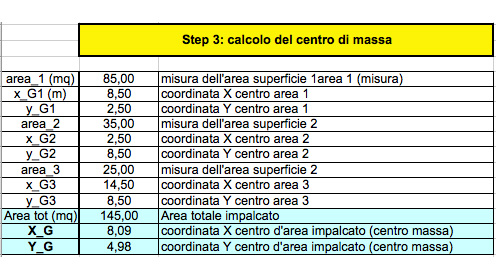
STEP 3: CALCOLO DEL CENTRO DI MASSA.

Come prima cosa dividiamo la struttura in tre aree per poi inserire i valori delle distanze dei loro baricentri dall’origine in modo da ricavarci le coordinate del baricentro dell’intero impalcato.

Xg = (A1 x  Xg1 + A2 x Xg2 + A3 x Xg3) / (A1 + A2 + A3)

Yg = (A1 x  Yg1 + A2 x Yg2 + A3 x Yg3) / (A1 + A2 + A3)

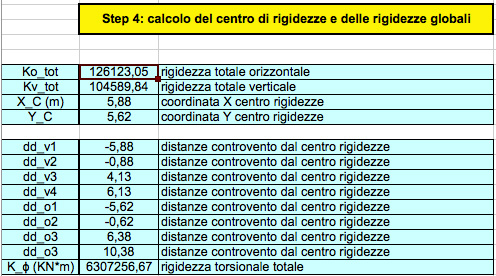
STEP 4: CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI.

In questa tabella vengono riportate le coordinate del centro delle rigidezze, punto intorno al quale ruota la struttura in caso di momento.  Considerando invece che il centro di massa è il punto nel quale vengono applicate le forze, la distanza tra i due punte risulta essere il braccio, di conseguenza più questi due punti si avvicinano e meno sarà importante il valore del momento!

Questa tabella ci permette inoltre di ricavarci la rigidezza torsionale totale (somma delle rigidezze di ogni telaio, moltiplicato per la loro distanza dal centro delle rigidezze.)

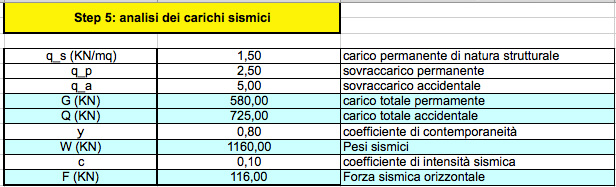
STEP 5: ANALISI DEI CARICHI SISMICI.

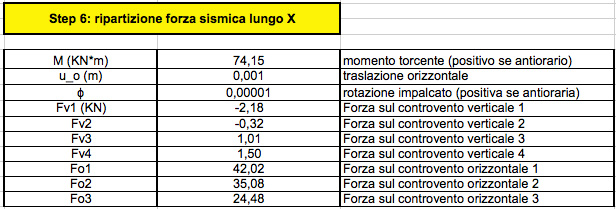
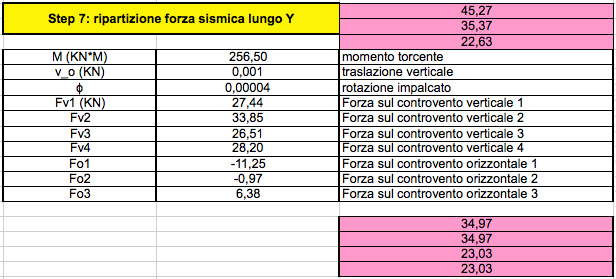
STEP 6-7: RIPARTIZIONE DELLA FORZA SISMICA LUNGO X E Y.

Queste ultime due tabelle ci riportano i valori del momento torcente della struttura, le traslazioni,  e le rotazioni lungo X  Y.