blog di bernardo.taliani

ESERCIZIO 1:

 

 

In questa prima esercitazione studieremo il comportamento torsionale di una struttura iperstatica in tre dimensioni, per poi verificarla tramite SAP2000.

Si tratta dunque di un telaio composto da tre aste vincolate ad incastro e da un'asta a sbalzosulla quale è applicato un carico distribuito q (10KN). Inoltre la struttura è 12 volte iperstatica (in 3d un incastro conta 6 gradi di vincolo) considerando 18 gdv e 6 gdl.

Lo sbalzo è di per sè isostatico quindi studiando i diagrammi delle sollecitazini, possiamo vedere come effetivamente esso sul nodo e possiamo sostituire la mensola con un momento (ricordiamo che consideriamo il pilastro assialmente indeformabile, possiamo perciò escludere l'azione dello sforzo normale).

Questo momento provoca una rotazione delle tre aste, creando due reazioni differenti: le due aste complanari reafiranno tramite la rigidezza flessionale e l'asta "perpendicolare" con la rigidezza torsionale. A questo punto possiamo risolvere l'iperstaticità delle struttura grazie al metodo della linea elastica:

riportiamo i momenti ricavati dall'eq. della inea elastica:

Equilibrio alla rotazione:

Mi ricavo la rigidezza (dove Ra è la somma delle rigidezze):

I momenti:

Ora l'obbiettivo è di capire in che modo la geometria delle sezioni ed il loro materiale influiscono sulla resistenza a torsione. Per fare ciò, prendiamo in esame quattro sezioni, due in acciaio (ipe, prof. scatolare) e due in cls (rettangolare e circolare), e confronteremo le loro restistenze (per facilitare la valutazione, le sezioni dello stesso manteriale hanno anche la stessa area).

Inizieremo mostrando i valori dei calcoli a mano per poi verificarli con SAP.

NB: oltre che con SAP possiamo verificare i risultati sommando i tre momenti, il risultato dovrà essere uguale a ql^2/2 (5KNm). Facendo ciò ho capito che le sezioni meno resistenti a torsione "obbligano" le aste inflesse a prendersi maggiore carico, tutto questo per un equilibrio più precario.

 

 

 

Esercizio 2:

 

In questo esercizio analizzeremo il comportamento di una struttura a graticcio di travi, ossia n intreccio di travi identiche ed ortogonali fra loro che, senza alcuna gerarchia collaborano per resistere ai carichi. Questo tipo di struttura può distinguersi tramite due particolarità: le travi essendo uguali devono avere tutte lo stesso momento d'inerzia e sopratutto devono avere il nodo ad incastro per trasmettere anche il momento.

Nel nostro caso studieremo la reazione di un graticcio semplice composto da due aste perpendicolari. Una di queste aste, essendo incastrata ad un terzo della sua lunghezza, provochera una rotazione che a sua volta genererà una torsione, tensione caratteristica di queste strutture.

 

Ogni corpo può traslare e ruotare in tre dimensioni, può dunque avere dodici gradi di libertà. Analizzando il nodo, sappiamo che non può ne traslare lungo x che lungo y dato che consideriamo le aste assialmente indeformabili, inoltre sappiamo che il nodo subisce una sola rotazione lungo l'asse y.

Le nostre variabili sono dunque due, lo spostamento lungo z e la rotazione lungo y.

Di seguito riportiamo gli "schemi noti" che torneranno utili per le varie equazioni di equilibrio:

A questo punto possiamo risolvere il problema grazie al metodo della sovrapposizione degli effetti:

Azione dovute all'abbassamento:

 

Azioni dovute alla rotazione del nodo:

 

I due equilibri (traslazione verticale e rotazione)

 

Ora possiamo sclegliere sezioni e materiali per confrontare i risultati.

 

 

 

In questa esercitazione, analizzeremo il comportamento di un impalcato strutturale soggetto a spinte orizzontali (ad esempio il vento o il sisma).

L’insieme di travi e pilastri, non solo riescono a resistere alle forze verticali ma se disposti correttamente nello spazio, possono anche fungere da controvento. I telai agiscono dunque come vincoli elastici, reagendo alle forze orizzontali lungo il loro stesso piano e proporzionalmente alla oro rigidezza, queste caratteristiche ci permettono di rappresentarli come vere e proprie molle!

 

A questo punto, consideriamo un impalcato in calcestruzzo armato (E=21000 N/mmq) composto da quattro  telai lungo X e quattro lungo Y, sorretti da dodici pilastri, questi ultimi avendo una dimensione di 30x40 cm e due momenti d’inerzia, uno lungo X e uno lungo Y.

 

Ora riportiamo lo stesso impalcato con rappresentate le molle e le loro distanze dall’origine.

 

Passiamo al foglio Excel grazie al quale ci ricaveremo i valori di reazione alle forze sismiche:

 

STEP 1: CALCOLO DELLE RIGIDEZZE TRASLANTIDEI CONTROVENTI DELL’EDIFICIO.

 

In queste tabelle inseriamo i valori di modulo elastico, dell’altezza dei pilastri e dei momenti d’inerzia dei pilastri (prendendo ovviamente quelli lungo l’asse del telaio studiato) per ricavarci la rigidezza traslante di ciascun telaio.

 

 

STEP 2: TABELLA SINOTTICA CONTROVENTI E DISTANZE.

 

Qui riportiamo le distanze verticali e orizzontali dei controventi dall’origine O.

 

 

STEP 3: CALCOLO DEL CENTRO DI MASSA.

 

Come prima cosa dividiamo la struttura in tre aree per poi inserire i valori delle distanze dei loro baricentri dall’origine in modo da ricavarci le coordinate del baricentro dell’intero impalcato.

Xg = (A1 x  Xg1 + A2 x Xg2 + A3 x Xg3) / (A1 + A2 + A3)

Yg = (A1 x  Yg1 + A2 x Yg2 + A3 x Yg3) / (A1 + A2 + A3)

 

STEP 4: CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI.

 

In questa tabella vengono riportate le coordinate del centro delle rigidezze, punto intorno al quale ruota la struttura in caso di momento.  Considerando invece che il centro di massa è il punto nel quale vengono applicate le forze, la distanza tra i due punte risulta essere il braccio, di conseguenza più questi due punti si avvicinano e meno sarà importante il valore del momento!

 

Questa tabella ci permette inoltre di ricavarci la rigidezza torsionale totale (somma delle rigidezze di ogni telaio, moltiplicato per la loro distanza dal centro delle rigidezze.)

 

 

 

 

STEP 5: ANALISI DEI CARICHI SISMICI.

 

 

 

STEP 6-7: RIPARTIZIONE DELLA FORZA SISMICA LUNGO X E Y.

Queste ultime due tabelle ci riportano i valori del momento torcente della struttura, le traslazioni,  e le rotazioni lungo X  Y.

TRAVE VIERENDEEL

 

In questo esercizio analizziamo una trave Vierendeel, ovvero una trave composta da due correnti collegati da montanti verticali con nodi ad incastro.

 

Si tratta dunque di una struttura internamente iperstatica e per risolverla possiamo considerare i montati infinitamente rigidi impedendo qualsiasi tipo di deformazione. In questo modo i collegamenti verticali non possono far altro che traslare verticalmente imprimendo una deformazione nei correnti orizzontali.

Lo studio di questa trave è dunque assimilabile a quello di un modello “shear type” dal quale riprenderemo i metodi di analisi.

 

Iniziamo con il calcolo delle reazioni di taglio del corrente orizzontale grazie all’equazione di equilibrio alla traslazione che eseguiremo separatamente in ognuno dei sei tratti.

tratto 2:

tratto 3:

tratto 4:

tratto 5:

tratto 6:

Disegno la deformata:

 

Per capire il diagramma del momento dei correnti orizzontali, possiamo osservare lo schema della deformata il quale ci indica che il punto di curvatura nullo (e di conseguenza il punto in qui il momento è pari a zero) si trova in mezzeria. Quindi possiamo capire che il valore del momento agli estremi delle aste orizzontali sarà pari al valore del taglio ricavato, moltiplicato per il braccio l/2.

 

 

Ora bisogna calcolare il valore del momento e del taglio delle aste verticali.

I momenti li troviamo facendo l’equilibrio alla rotazione delle aste verticali.

 

 

Il taglio va trovato equilibrando ai momenti appena ricavati una coppia di forze. 

Per finire i due diagrammi:

Confronto i risultati con SAP:

TRAVE VIERENDEEL DOPPIAMENTE APPOGGIATA

 

Questa volta analizzeremo nuovamente la trave vierendeel con la differenza che verrà vincolata in entrambi i bordi, e come in precedenza ci ricaveremo i valori di taglio, momento e spostamento di tutte le aste.

Notiamo come a differenza di prima, la struttura è perfettamente simmetrica, un aspetto che ci semplifichera molto i calcoli!

Partendo dal tratto centrale, analizziamo le reazioni alle forze verticali:

(come prima per ricavare il momento dei correnti orizzontali basta moltiplicare il valore del taglio per l/2)

disegno la deformata:

Equilibrio al nodo per ricavare il valore del momento delle aste verticali:

Equilibrio delle aste verticali per calcolare il valore del taglio:

Diagramma del taglio:

Diagramma del momento:

Confronto i risultati con SAP:

 

Si tratta di una struttura 3 volte iperstatica e per risolverla conviene considerarla come una serie di travi doppiamente appoggiate (e non come un unico corpo). Usiamo dunque un sistema isostatico di riferimento “togliendo” a quello iperstatico i vincoli di rigidità ai carrelli B, C e D (trasformando le cerniere passanti in cerniere interne) e applicando dei momenti flettenti X1, X2 e X3 in modo da ripristinare la rigidità della trave.

Notiamo inoltre che si tratta di un sistema simmetrico, questo ci permette di semplificare i calcoli considerando X1=X3.

 

A questo punto possiamo calcolarci le incognite X1 e X2 grazie ai valori della rotazione nei punti B, C e D:

Sappiamo che ΔφB=ΔφD=0 e ΔφC=0

 

Ora uguagliamo i valori della rotazione di sinistra con quelli di destra e ricaviamo X1 e X2.

 

 

A questo punto abbiamo trovato le due incognite e possiamo procedere con il calcolo delle reazioni vincolari.

Per semplificare i calcoli le calcoliamo prima considerando unicamente il carico distribuito e successivamente con i momenti flettenti, per poi sommarle e trovare quelle del sistema iperstatico.

 

Infine disegniamo i diagrammi di sollecitazione del taglio e momento.

Per trovare i valori del diagramma del momento eseguiamo dei tagli dove il taglio risulta nullo (e quindi dove il momento è massimo) ed in corrispondenza degli appoggi.  

Disegno un telaio strutturale composto da travi in acciaio, ipotizzando una destinazione d'uso residenziale.

La trave maggiormente sollecitata è la trave 1-2 lungo l'allineamento B

L=6,7m

I=3,35m

ANALISI DEI CARICHI:

Ora possiamo iniziare l'analisi dei carichi per poter dimensionare trave e travetti.

 

Qa (carichi accidentali): 2,00 KN/mq

 

Qp (carichi permanenti): 3,02 KN/mq

 

      -Isolante termo-acustico (sp. 4cm): 7,1KN/mc x 0,04m = 0,28KN/mq

      -Massetto (sp. 4cm): 21KN/mc x 0,04m = 0,84KN/mq

      -Tramezzi + impianti: 1,5 KN/mq

      -Pavimentazione in gres (sp. 2cm): 20KN/mc x 0,02m = 0,4 KN/mq

 

Qs (carichi strutturali):

 

Dimensionamenti travetto

Devo trovare qual è il modulo di resistenza Wx che i travetti devono sopportare, mi calcolo dunque il Qs considerando unicamente il peso della lamiera grecata.

Scelgo dunque una lamiera grecata A55/P600 con getto in cls per uno spessore totale di 11 cm.: 1,15 KN/mq

 

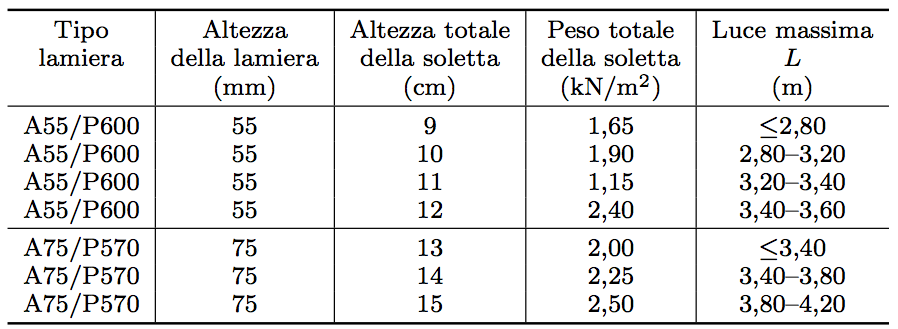
Ora posso inserire i valori nella tabella Excel per un travetto di luce 3,35m e interasse di 1m.

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fy,k (N/mm2)	sigam (N/mm2)	Wx (cm3)
1	1,15	3,02	2,00	6,17	3,35	8,655353125	275	239,13	36,20

 

Ricavo una Wx di 36,20mc e scelgo una IPE 120 (Wx 53 cm3) con un peso di 10,4 Kg/m.

Per trovare il valore in mq, lo divido per la lunghezza dell’interasse:  0,104KN/m / 1m = 0,104 KN/mq

 

Dimensionamento trave

 

A questo punto sommiamo il valore appena trovato con quello della lamiera grecata per trovare il Qs che agisce sulla trave principale:

Qs = 0,104 KN/mq + 1,15 KN/mq = 1,25 KN/mq

Inserisco sulla tabella il nuovo valore di Qs con una luce di 6,7m ed un interasse di 3,35m.

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fy,k (N/mm2)	sigam (N/mm2)	Wx (cm3)
1	1,15	3,02	2,00	6,17	3,35	8,655353125	275	239,13	36,20
3,35	1,25	3,02	2,00	21,0045	6,7	117,8615006	275	239,13	492,88

 

Mi ricavo un modulo di resistenza Wx = 492,88mc

 

Scelgo una IPE 300 (Wx: 557cm3) con peso pari a 42,2Kg/m che divido per l’interasse di 3,35m trovando un peso specifico di 0,12KN/mq

 

Per finire calcolo il carico strutturale totale e verifico se il modulo di resistenza della IPE 300 rispetta quello minimo.

 

Qs.tot: 1,25 KN/mq + 0,12 KN/mq = 1,37 KN/mq

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fy,k (N/mm2)	sigam (N/mm2)	Wx (cm3)
1	1,15	3,02	2,00	6,17	3,35	8,655353125	275	239,13	36,20
3,35	1,25	3,02	2,00	21,0045	6,7	117,8615006	275	239,13	492,88
3,35	1,37	3,02	2,00	21,4065	6,7	120,1172231	275	239,13	502,31

 

502,3cm3 < 557 cm3 il solaio è verificato.

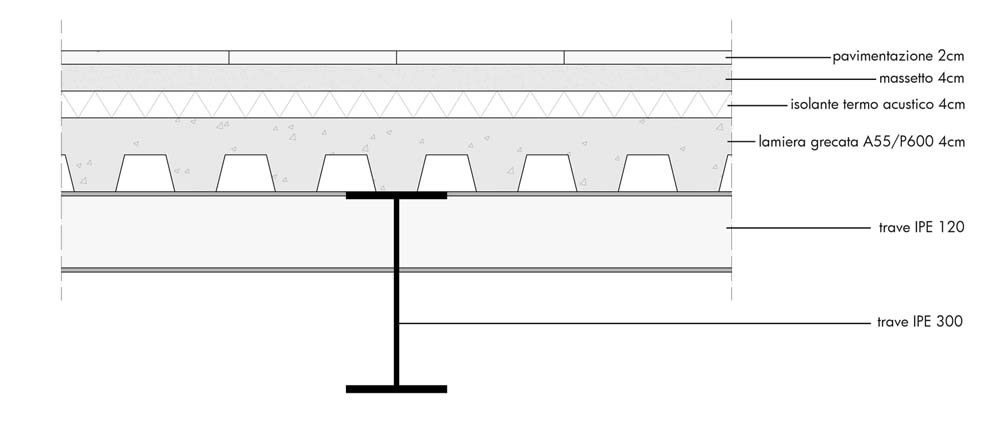
SOLAIO IN LEGNO

 

Come per il solaio in acciaio, definiamo prima i carichi permanenti e accidentali per poi dimensionare travetti e trave principale con l'analisi dei carichi strutturali.

-CARICO PERMANENTE NON STRUTTURALE (Qp): 3,564 KN/mq

• getto in cls: peso specifico: 20KN/mc; spessore: 0,04m---------->0,8 KN/mq
• isolante termo-acustico: peso sp: 7KN/mc; sp.: 0,04m----------->0,28 KN/mq
• massetto: peso sp.:21KN/mc; sp.:0,04m----------------------->0,84 KN/mq
• tramezzi+impianti ----------------------------------------->1,5KN/mq
• pavimentazione in legno di rovere: peso sp:7,2KN/mc; sp.:0,02m-->0,144 KN/mq          

-CARICO ACCIDENTALE (QA): 2,00 KN/mq         

• ambiente ad uso residenziale: 2KN/mq come da normativa

-PROGETTO TRAVETTI: L: 3,35m_ I: 1m

Calcoliamo il carico strutturale considerando unicamente il peso del tavolato di legno, spesso 4cm

Qs= 6KN/mc x 0,04m = 0,24 KN/mq

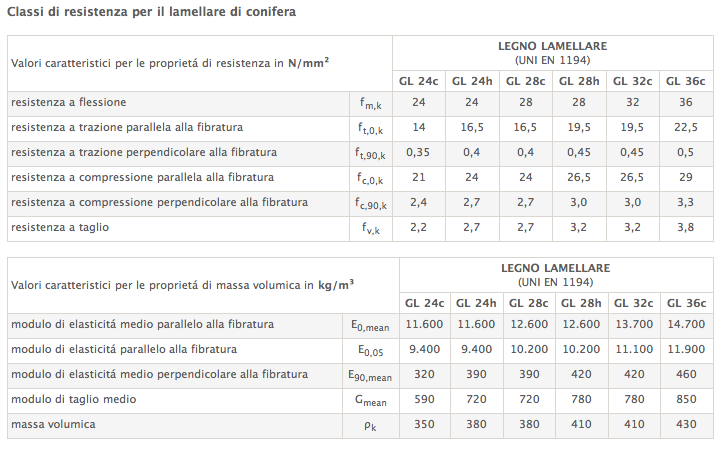
Scelgo un travetto in legno lamellare di tipo GL 24c (fm,k: 24K N/mmq)

Il valore di Kmod (durata del materiale) viene ricavato dalla tabella scegliendo la classe di servizio 1 ed una durata permanente. Il valore fissato è Kmod=0.6

Inserisco i valori nella tabella Excel e scelgo una base per il travetto di 12cm. Ottengo un'altezza minima di 20,24 cm che approssimiamo a 24cm.

 

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fm,k (N/mm2)	kmod	sigam (N/mm2)	b (cm)	h (cm)
1	0,24	3,56	2,00	5,8	3,35	8,1363125	24	0,6	9,93	12	20,24

-VERIFICA DEL TRAVETTO

• peso specifico Gl 24c: 350 Kg/mc
• peso travetto: 0,12m x 0,24m x 3,35m x 3,5 KN/mc = 0,33 KN
• peso al mq: 0,33KN / (1 x 3,35 mq) = 0,1 KN/mq 
• Qs = 0,34 KN/mq

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fm,k (N/mm2)	kmod	sigam (N/mm2)	b (cm)	h (cm)
1	0,34	3,56	2,00	5,9	3,35	8,27659375	24	0,6	9,93	12	20,41

Risulta un'altezza di 20,41 cm, avendone scelta una di 24, il travetto è verificaro!

-PROGETTO TRAVE: L: 6,7m I:1m

A questo punto i valori dei carichi e del Kmod rimangono invariati, cambiano la luce, l'interasse e il valore fm,k, avendo scelto per la trave un legno lamellare GL 36c (fm,k: 36 KN/mmq)

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fm,k (N/mm2)	kmod	sigam (N/mm2)	b (cm)	h (cm)
3,35	0,34	3,56	2,00	19,765	6,7	110,9063563	36	0,6	14,90	25	42,27

Avendo ipotizzato una base di 25 cm, ottengo un'altezza di 42,27 cm, approssimata a 45cm.

-VERIFICA DELLA TRAVE:

• peso specifico: 430 Kg/mc
• peso trave: 4,3 KN/mc x 0,25m x 0,45m x 6,7m = 3,25 KN
• peso al mq: 3,25 KN / (3,35 x 6,7 mq) = 0,15 KN/mq
• Qs= 0,49 KN/mq 

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fm,k (N/mm2)	kmod	sigam (N/mm2)	b (cm)	h (cm)
3,35	0,49	3,56	2,00	20,2675	6,7	113,7260094	36	0,6	14,90	25	42,80

Otteniamo un'altezza di 42,80cm

42,80cm < 45 cm ------------> LA TRAVE è VERIFICATA!

 

 

SOLAIO IN CLS

 

-CARICO PERMANENTE NON STRUTTURALE Qp=3,02 KN/mq

• pavimentazione in gres (sp. 2 cm): 20 KN/mq x 0,02m = 0,4 KN/mq
• massetto (sp. 4cm): 21KN/mc x 0,04 m= 0,84 KN/mq
• isolante termo-acustico (sp. 4cm): 7,1 KN/mc x 0,04 m = 0,28 KN/mq
• tramezzi + impianti = 1,5 KN/mq

 

-CARICO ACCIDENTALE Qa = 2 KN/mq

 

-CARICO STRUTTURALE Qs: 3,26 KN/mq

Scelgo un solaio in laterocemento in grado di coprire una luce massima di 3,60m (>3,35m) con uno spessore di 20cm ed un peso proprio di 236Kg/mq.

Inoltre scelgo di usare un cls35/45 (Rck: 45 N/mmq), un acciaio B450C con un copriferro (delta) di 5 cm.

risultati exell:

interasse (m)    qs (KN/m2)    qp (KN/m2)    qa (KN/m2)    q (KN/m)    luce (m)    M (KN*m)    fy (N/mm2)    sig_fa (N/mm2)    Rck (N/mm2)
                                   
      3,35                2,36              3,02                2,00           24,723         6,7        138,726           450                 391,30                  45

 

sig_ca (N/mm2)    alfa          r         b (cm)    h (cm)    delta (cm)    H (cm)       H/l      area (m2)    peso (KN/m)
                                   
       25,50           0,49       2,20          30       29,64         5             34,64    0,052       0,10               2,60

 

Risulta una altezzapari a 34,64 cm che porteremo a 40 cm (le travi in cls vengono generalmente realizzate ogno 5 cm)

Oa verifichiamo il tutto aggiungendo al Qs il peso proprio della trave:

• peso proprio trave 30x40: 3,00 KN/m
• peso trave al mq: 3,00/3,35 KN/mq = 0,9 KN/mq

risultati exell:

interasse (m)    qs (KN/m2)    qp (KN/m2)    qa (KN/m2)    q (KN/m)    luce (m)    M (KN*m)    fy (N/mm2)    sig_fa (N/mm2)    Rck (N/mm2)
                                   
     3,35                 3,26                3,02              2,00           27,738        6,7          155,64            450                391,30                 45

 

sig_ca (N/mm2)    alfa        r        b (cm)        h (cm)       delta (cm)      H (cm)           H/l          area (m2)      peso (KN/m)
                                   
      25,50             0,49     2,20      30            31,39            5               36,39          0,054           0,11                  2,73

 

Otteniamo un' altezza  di 36,39cm

36,39cm < 40cm -------------> LA TRAVE è VERIFICATA!

 

 

 

La travatura reticolare piana è un insieme di aste complanari vincolate ai nodi con cerniere interne, sulle quali agisce il solo sforzo normale.

Per analizzare queste strutture esistono due metodi principali: Il metodo dei nodi e quello delle sezioni di Ritter.

 

METODO DELLE SEZIONI:

Calcoliamo le reazioni vincolari:

Applichiamo le sezioni:

La prima sezione la effetuisco in modo da tagliare tre aste e permettondomi di realizzare in seguito gli equilibri con valori noti.

Grazie alla simmetria della struttura posso disegnare il risultato senza dover calcolare la seconda parte della struttura.

 

VERIFICA SU SAP, ecco i passaggi:

 

-Disegnare una trave reticolare tramite la funzione "trusses"

-Assegnare i vincoli e definire un peso nullo.

-Creare la sezione: Define_Frame section_Pipe

-Assegnare un carico puntuale selezionando l’asta superiore e cliccando su:
Assign_joint_forces e sulla casella di ‘global z’ inserire un carico negativo di 20 MPA.

-Selezionare la struttura e cliccare: Assign_frames_releases e selezionare moment 3-3 (per fare in modo che ogni asta sia collegata ad una cerniera con momento 0-0).

-Far partire l’analisi con ‘run now’ e verificare la deformata ed i diagrammi dello sforzo assiale.

-Cliccare sull’icona ‘v’ (set display options) e selezionare ‘labels’ per vedere la numerazione delle aste.

-Infine per conoscere gli sforzi normali di ciascuna asta seguire il seguente passaggio: Display_Show tables_Analisys results. In questa tabella è possibile osservare in che modo lavora ogni asta con dei valori ogni 50 cm.

 

-TRAVE RETICOLARE SPAZIALE (sap):

 

Prima di aprire il programma disegnamo la travatura con autocad 3D (evitando di disegnare con il layer 0).

Apriamo SAP e importiamo il disegno salvato precedentemente in dxf.

Selezionare tutto e cliccare: edit_edit points_erge joints_merge tolerance_0,01 (per impostare una tolleranza di errore di 1 cm)

Assegno tre vincoli: una cerniera e due carrelli: assign_joint restraints (ricordiamo di non impostare i vincoli su un'asse unico)

Assegnamo il materiale usando una sezione tubolare di diametro 10 cm e spessore 0,5 cm

Assegnamo un peso proprio nullo (in modo da analizzare unicamente l'azione dei carichi e delle forze esterne.)

Asegnamo ai nodi delle cerniere interne: assign_frame_releases_moment3-3_0

Assegnamo ai nodi superiori un carico di 50 KN sull'asse z

Lanciamo l'analisi con "run now" (considerando unicamente il peso nullo)

deformata:

diagrammi sforzo normale: (show forces_frames_axial forces)

per visualizzare le reazioni vincolare cliccare: show forces_joints

con   display_show tables_elements forces frames   possiamo analizzare gli sforzi assiali di ogni singola asta.

Le aste con valori di sforzo assiale positivo sono tiranti, quelle con valore negativo sono puntoni.