ESERCITAZIONE_metodo delle forze

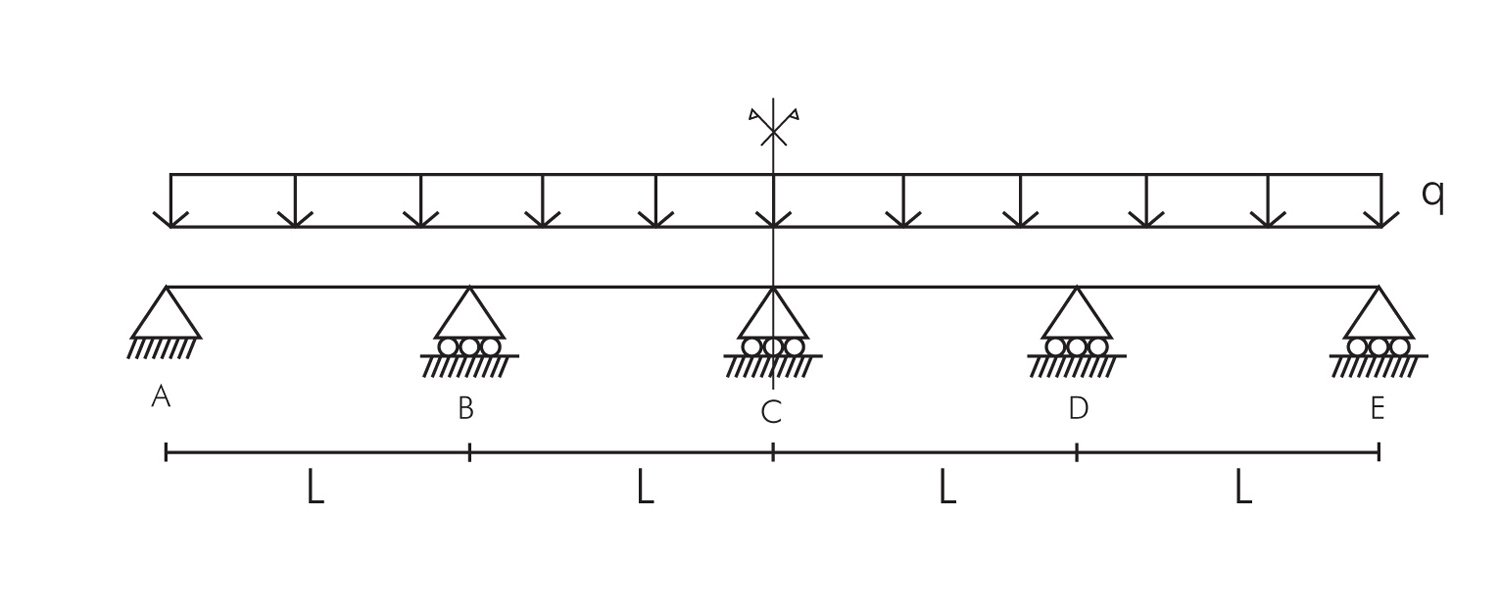
Si tratta di una struttura 3 volte iperstatica e per risolverla conviene considerarla come una serie di travi doppiamente appoggiate (e non come un unico corpo). Usiamo dunque un sistema isostatico di riferimento “togliendo” a quello iperstatico i vincoli di rigidità ai carrelli B, C e D (trasformando le cerniere passanti in cerniere interne) e applicando dei momenti flettenti X1, X2 e X3 in modo da ripristinare la rigidità della trave.

Notiamo inoltre che si tratta di un sistema simmetrico, questo ci permette di semplificare i calcoli considerando X1=X3.

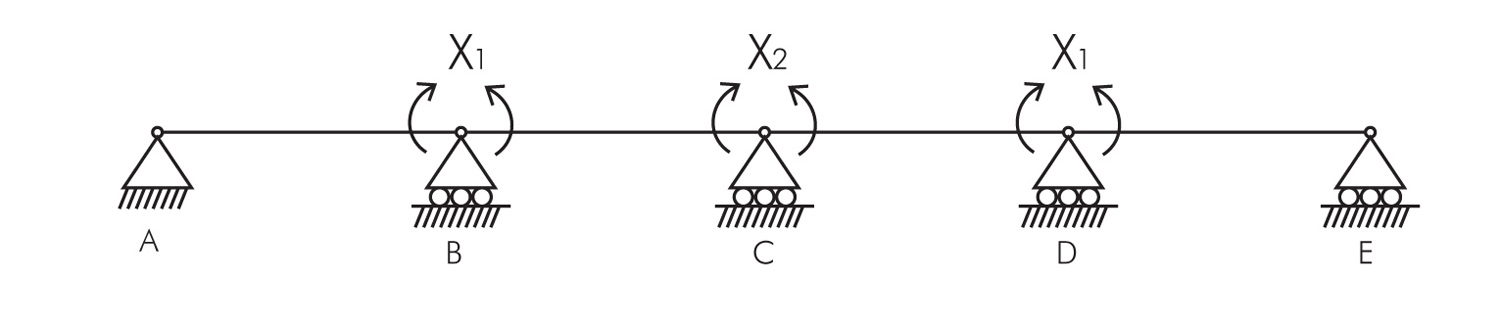
A questo punto possiamo calcolarci le incognite X1 e X2 grazie ai valori della rotazione nei punti B, C e D:

Sappiamo che ΔφB=ΔφD=0 e ΔφC=0

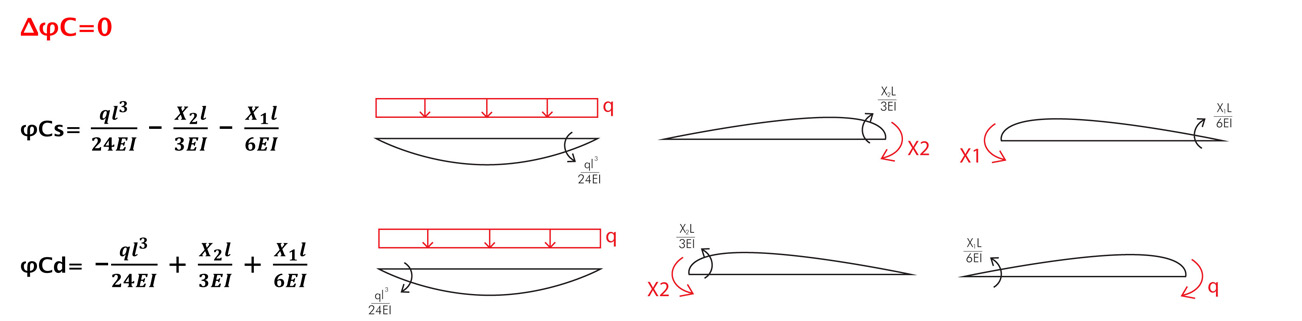
Ora uguagliamo i valori della rotazione di sinistra con quelli di destra e ricaviamo X1 e X2.

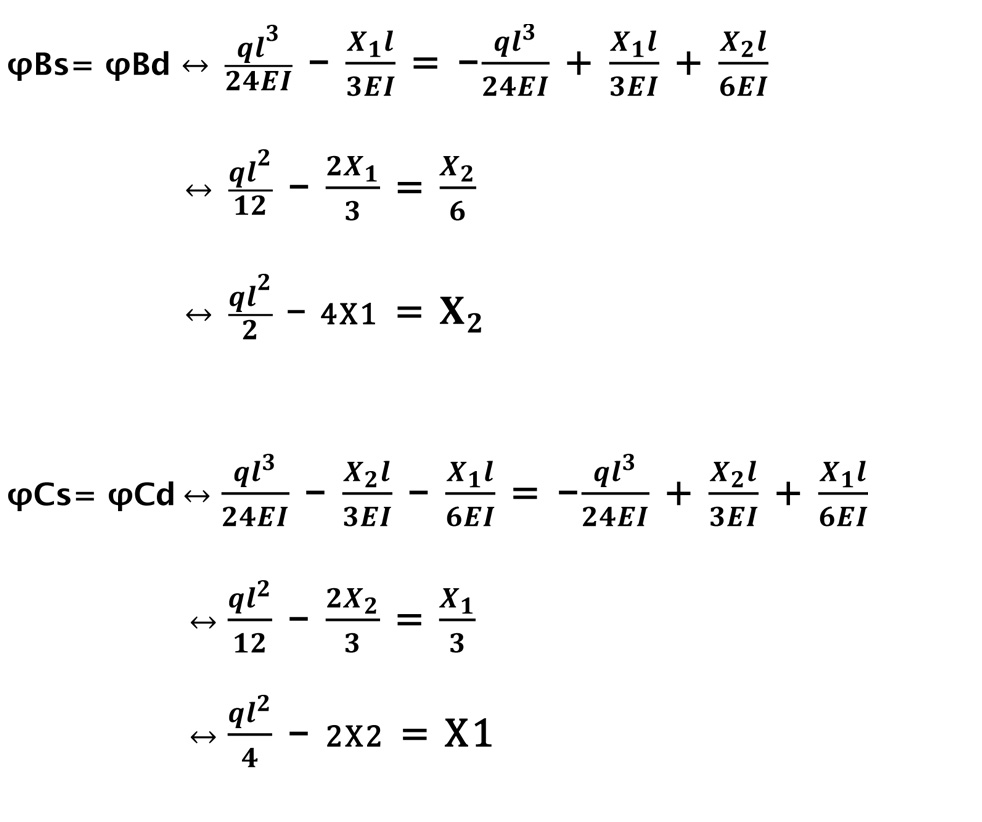
A questo punto abbiamo trovato le due incognite e possiamo procedere con il calcolo delle reazioni vincolari.

Per semplificare i calcoli le calcoliamo prima considerando unicamente il carico distribuito e successivamente con i momenti flettenti, per poi sommarle e trovare quelle del sistema iperstatico.

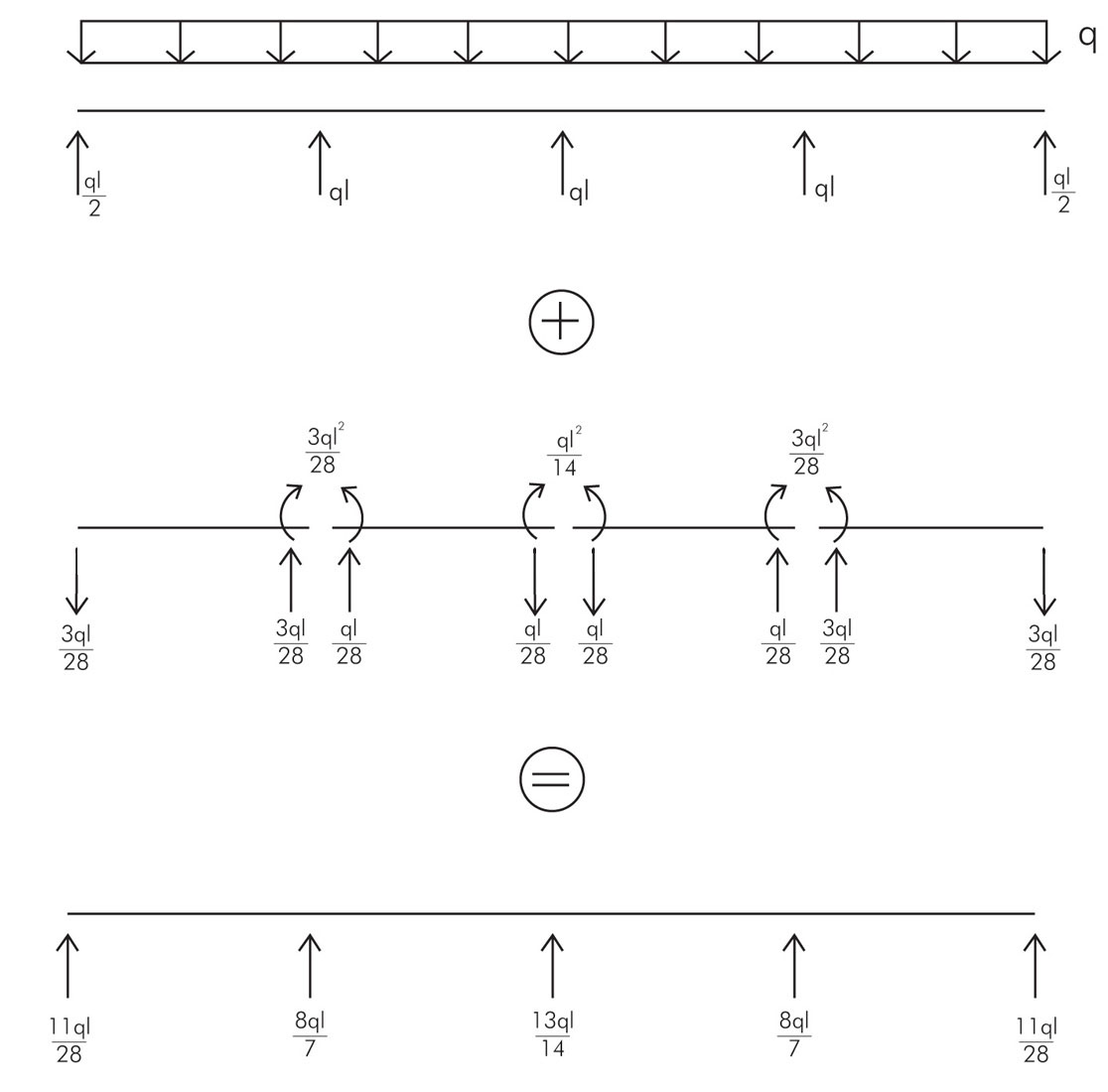
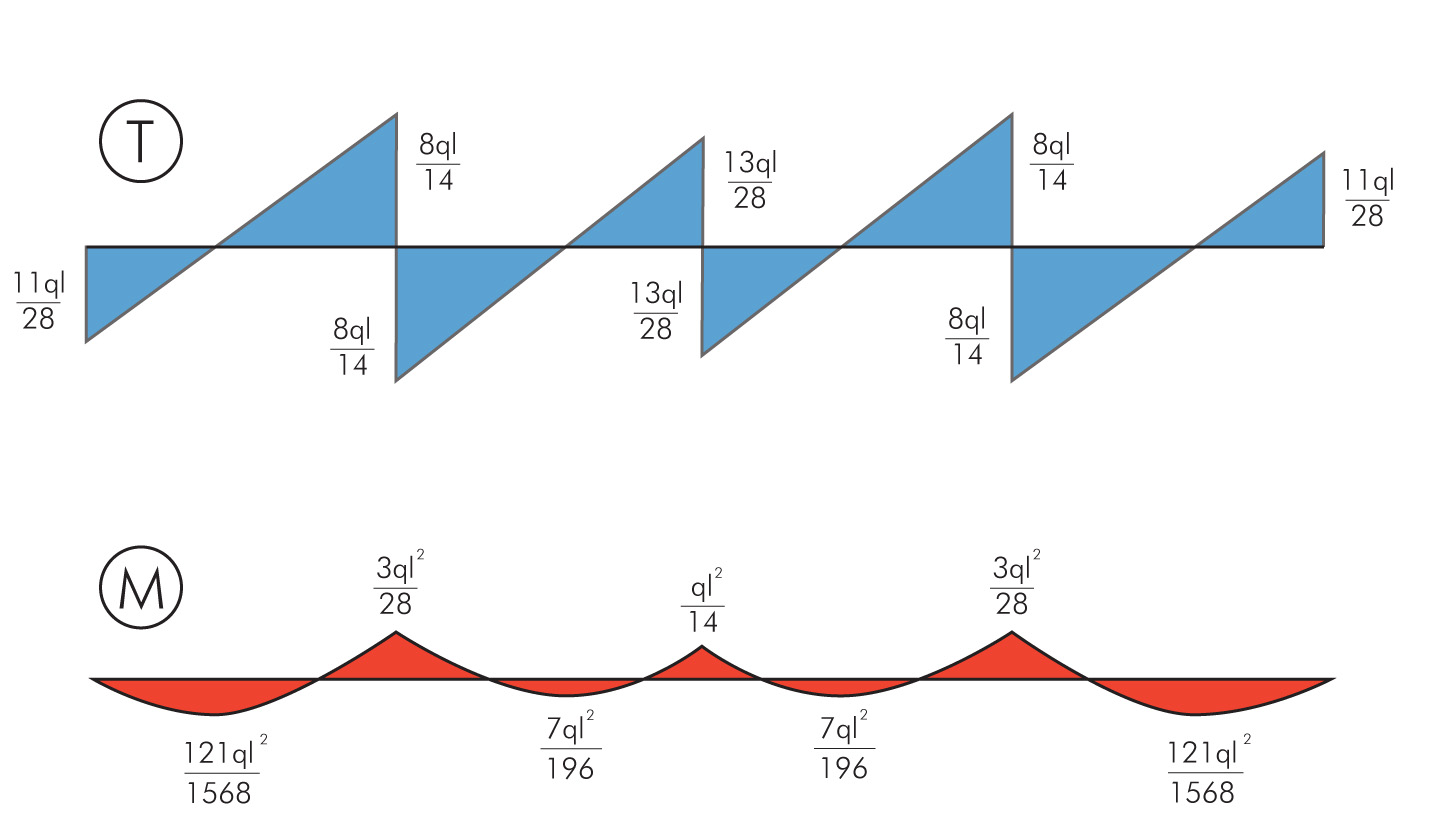
Infine disegniamo i diagrammi di sollecitazione del taglio e momento.

Per trovare i valori del diagramma del momento eseguiamo dei tagli dove il taglio risulta nullo (e quindi dove il momento è massimo) ed in corrispondenza degli appoggi.